11.1: Secuencias y sus anotaciones

Última actualización
Guardar como PDF

Page ID: 121354

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Escribir los términos de una secuencia definida por una fórmula explícita.
Escribe los términos de una secuencia definida por una fórmula recursiva.
Usar notación factorial.

Una compañía de videojuegos lanza una nueva y emocionante campaña publicitaria. Predicen que el número de visitas en línea a su sitio web, o visitas, se duplicará cada día. El modelo que están usando muestra$2$ golpea el primer día,$4$ golpea el segundo día,$8$ golpea el tercer día, y así sucesivamente (Tabla$\PageIndex{1}$).

Mesa$\PageIndex{1}$
Día	1	2	3	4	5	...
Éxitos	2	4	8	16	32	...

Si su modelo continúa, ¿cuántos éxitos habrá a fin de mes? Para responder a esta pregunta, primero necesitaremos saber cómo determinar una lista de números escritos en un orden específico. En esta sección, exploraremos este tipo de listas ordenadas.

Escribir los términos de una secuencia definida por una fórmula explícita

Una forma de describir una lista ordenada de números es como una secuencia. Una secuencia es una función cuyo dominio es un subconjunto de los números de conteo. La secuencia establecida por el número de visitas en el sitio web es

$\{ 2,4,8,16,32,…\}$

Los puntos suspensivos (...) indican que la secuencia continúa indefinidamente. Cada número en la secuencia se llama término. Los primeros cinco términos de esta secuencia son$2$,$4$,$8$,$16$, y$32$.

Enumerar todos los términos para una secuencia puede ser engorroso. Por ejemplo, encontrar el número de visitas en el sitio web al final del mes requeriría enumerar tantos como$31$ términos. Una forma más eficiente de determinar un término específico es escribiendo una fórmula para definir la secuencia.

Un tipo de fórmula es una fórmula explícita, que define los términos de una secuencia usando su posición en la secuencia. Las fórmulas explícitas son útiles si queremos encontrar un término específico de una secuencia sin encontrar todos los términos anteriores. Podemos usar la fórmula para encontrar el término n de la secuencia, donde nn es cualquier número positivo. En nuestro ejemplo, cada número de la secuencia es el doble del número anterior, por lo que podemos usar potencias de 2 para escribir una fórmula para el enésimo término.

$Secuencia de {2, 4, 8, 16, 32,...} expresada en forma exponencial (es decir, {2^1, 2^2, 2^3,..., 2^n,...}$

El primer término de la secuencia es$2^1=2$, el segundo término es$2^2=4$, el tercer término es$2^3=8$, y así sucesivamente. El enésimo término de la secuencia se puede encontrar elevando 2 a la enésima potencia. Una fórmula explícita para una secuencia se nombra por una letra minúscula$a$$b$,,$c$... con el subíndice$n$. La fórmula explícita para esta secuencia es

$a_n=2^n$

Ahora que tenemos una fórmula para el enésimo término de la secuencia, podemos responder a la pregunta planteada al inicio de esta sección. Nos pidieron que encontráramos el número de aciertos a fin de mes, que tardaremos en ser de 31 días. Para encontrar el número de aciertos en el último día del mes, necesitamos encontrar el 31 ^er término de la secuencia. Vamos a sustituir 31 por$n$ en la fórmula.

\[ \begin{align*} a_{31}=2^{31} \\ [5pt] &=2,147,483,648 \end{align*}\]

Si la tendencia de duplicación continúa, la compañía recibirá$2,147,483,648$ hits el último día del mes. ¡Eso es más de$2.1$ mil millones de hits! El enorme número probablemente sea un poco poco realista porque no toma en cuenta el interés del consumidor y la competencia. Sin embargo, le da a la empresa un punto de partida desde el cual considerar las decisiones de negocio.

Otra forma de representar la secuencia es mediante el uso de una tabla. Los primeros cinco términos de la secuencia y el enésimo término de la secuencia se muestran en la Tabla$\PageIndex{2}$.

**Mesa$\PageIndex{2}$**
$n$	1	2	3	4	5	$n$
$n^{th}$término de la secuencia,$a_n$	2	4	8	16	32	$2^n$

La gráfica proporciona una representación visual de la secuencia como un conjunto de puntos distintos. Podemos ver en la gráfica de la Figura$\PageIndex{1}$ que el número de aciertos está aumentando a un ritmo exponencial. Esta secuencia particular forma una función exponencial.

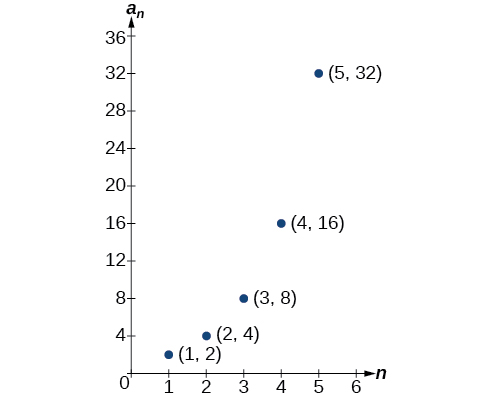
$Gráfico de una función exponencial trazada, f (n) = 2^n, donde el eje x se etiqueta n y el eje y se etiqueta a_n.$

Figura$\PageIndex{1}$

Por último, podemos escribir esta secuencia en particular como

$\{2,4,8,16,32,…,2^n,…\}$

Una secuencia que continúa indefinidamente se denomina secuencia infinita. El dominio de una secuencia infinita es el conjunto de números de conteo. Si consideramos sólo los primeros$10$ términos de la secuencia, podríamos escribir

$\{2,4,8,16,32,…,2^n,…,1024\}$

Esta secuencia se denomina secuencia finita porque no continúa indefinidamente.

SECUENCIA

Una secuencia es una función cuyo dominio es el conjunto de enteros positivos. Una secuencia finita es una secuencia cuyo dominio consiste únicamente en los primeros enteros$n$ positivos. Los números en una secuencia se llaman términos. La variable$a$ con un subíndice numérico se utiliza para representar los términos en una secuencia y para indicar la posición del término en la secuencia.

\[a_1,a_2,a_3,…,a_n,…\]

Llamamos$a_1$ al primer término de la secuencia,$a_2$ al segundo término de la secuencia,$a_3$ al tercer término de la secuencia, y así sucesivamente. El término$a_n$ se llama el enésimo término de la secuencia, o el término general de la secuencia. Una fórmula explícita define el término n de una secuencia usando la posición del término. Una secuencia que continúa indefinidamente es una secuencia infinita.

Q&A: ¿Una secuencia siempre tiene que empezar por$a_1$?

No. En ciertos problemas, puede ser útil definir el término inicial como$a_0$ en lugar de$a_1$. En estos problemas, el dominio de la función incluye$0$.

Cómo: Dada una fórmula explícita, escribir la primera$n$ terms of a sequence

Sustituir cada valor de$n$ en la fórmula. $n=1$Empezar por encontrar el primer término,$a_1$.
Para encontrar el segundo término,$a_2$, utilizar$n=2$.
Continúe de la misma manera hasta que haya identificado todos los términos nn.

Ejemplo$\PageIndex{1}$: Writing the Terms of a Sequence Defined by an Explicit Formula

Escribe los primeros cinco términos de la secuencia definida por la fórmula explícita$a_n=−3n+8$.

Solución

Sustituir$n=1$ en la fórmula. Repita con valores$2$ a través$5$ de for$n$.

$\begin{array}{ll} n=1 & a_1=−3(1)+8=5 \\ n=2 & a_2=−3(2)+8=2 \\ n=3 & a_3=−3(3)+8=−1 \\ n=4 & a_4=−3(4)+8=−4 \\ n=5 & a_5=−3(5)+8=−7 \end{array}$

Los primeros cinco términos son$\{5,2,−1,−4,−7\}$.

Análisis

Los valores de secuencia se pueden enumerar en una tabla. Una tabla, como Table$\PageIndex{3}$, es una forma conveniente de ingresar la función en una utilidad gráfica.

Mesa$\PageIndex{3}$
$n$	1	2	3	4	5
$a_n$	5	2	—1	—4	—7

Se puede hacer una gráfica a partir de esta tabla de valores. A partir de la gráfica de la Figura$\PageIndex{2}$, podemos ver que esta secuencia representa una función lineal, pero observe que la gráfica no es continua porque el dominio está sobre los enteros positivos solamente.

$Gráfica de una gráfica dispersa donde el eje x se etiqueta n y el eje y se etiqueta a_n.$

Figura$\PageIndex{2}$

Ejercicio$\PageIndex{1}$

Escribe los primeros cinco términos de la secuencia definida por la fórmula explícita$t_n=5n−4$.

Contestar: Los primeros cinco términos son$\{1,6, 11, 16, 21\}$.

Investigación de secuencias alternas

A veces las secuencias tienen términos que son alternos. De hecho, los términos en realidad pueden alternar en señal. Los pasos para encontrar términos de la secuencia son los mismos que si los signos no se alternaran. Sin embargo, los términos resultantes no mostrarán incremento o disminución como$n$ incrementos. Echemos un vistazo a la siguiente secuencia.

$\{2,−4,6,−8\}$

Observe que el primer término es mayor que el segundo término, el segundo término es menor que el tercer término, y el tercer término es mayor que el cuarto término. Esta tendencia continúa para siempre. No reorganizar los términos en orden numérico para interpretar la secuencia.

Cómo: Dada una fórmula explícita con términos alternos, escribir los primeros términos nn de una secuencia

Sustituir cada valor de nn en la fórmula. $n=1$Empezar por encontrar el primer término,$a_1$. El signo del término viene dado por el${(−1)}^n$ en la fórmula explícita.
Para encontrar el segundo término,$a_2$, utilizar$n=2$.
Continúe de la misma manera hasta que haya identificado todos los$n$ términos.

Ejemplo$\PageIndex{2}$: Writing the Terms of an Alternating Sequence Defined by an Explicit Formula

Escribe los primeros cinco términos de la secuencia.

$a_n=\dfrac{{(−1)}^nn^2}{n+1}$

Solución

Sustituir$n=1$$n=2$,, y así sucesivamente en la fórmula.

$\begin{array}{ll} n=1 & a_1=\dfrac{{(−1)}^12^2}{1+1}=−\dfrac{1}{2} \\ n=2 & a_2=\dfrac{{(−1)}^22^2}{2+1}=\dfrac{4}{3} \\ n=3 & a_3=\dfrac{{(−1)}^33^2}{3+1}=−\dfrac{9}{4} \\ n=4 & a_4=\dfrac{{(−1)}^44^2}{4+1}=\dfrac{16}{5} \\ n=5 & a_5=\dfrac{{(−1)}^55^2}{5+1}=−\dfrac{25}{6} \end{array}$

Los primeros cinco términos son$\{−12,43,−94,165,−256\}$.

Análisis

La gráfica de esta función, mostrada en la Figura$\PageIndex{3}$, se ve diferente a las que hemos visto anteriormente en esta sección porque los términos de la secuencia alternan entre valores positivos y negativos.

$Gráfica de una parcela dispersa con puntos etiquetados: (1, -1/2), (2, 4/3), (3, -9/4), (4, 16/5) y (5, -25/6). El eje x se etiqueta n y el eje y se etiqueta como a_n.$

Figura$\PageIndex{3}$

Q&A: En el ejemplo anterior, ¿el$(–1)$ to the power of $n$ account for the oscillations of signs?

Sí, el poder podría ser$n$$n+1$,$n−1$, y así sucesivamente, pero cualquier poder extraño resultará en un término negativo, y cualquier poder par resultará en un término positivo.

Ejercicio$\PageIndex{2}$

Escribe los primeros cinco términos de la secuencia:

$a_n=\dfrac{4n}{{(−2)}^n}$

Contestar: Los primeros cinco términos son$\{−2, 2, −32, 1, −58\}$.

Investigando fórmulas explícitas por partes

Hemos aprendido que las secuencias son funciones cuyo dominio está sobre los enteros positivos. Esto es cierto para otros tipos de funciones, incluidas algunas funciones por partes. Recordemos que una función por partes es una función definida por múltiples subsecciones. Una fórmula diferente podría representar cada subsección individual.

Cómo: Dada una fórmula explícita para una función por partes, escriba la primera$n$ terms of a sequence

Identificar la fórmula a la que$n=1$ se aplica.
Para encontrar el primer término,$a_1$, utilizar$n=1$ en la fórmula apropiada.
Identificar la fórmula a la que$n=2$ se aplica.
Para encontrar el segundo término,$a_2$, utilizar$n=2$ en la fórmula apropiada.
Continúe de la misma manera hasta que haya identificado todos los$n$ términos.

Ejemplo$\PageIndex{3}$: Writing the Terms of a Sequence Defined by a Piecewise Explicit Formula

Escribe los primeros seis términos de la secuencia.

$a_n=\begin{cases}n^2\space \text{if n is not divisible by } 3\\\dfrac{n}{3} \text{if n is divisible by } 3\end{cases}$

Solución

Sustituir$n=1$$n=2$,, y así sucesivamente en la fórmula apropiada. Usar$n^2$ cuando no$n$ es un múltiplo de$3$. Usar$n^3$ cuando$n$ es un múltiplo de$3$.

$\begin{array}{ll} a_1=1^2=1 & 1 \text{ is not a multiple of }3. \text{ Use } n^2. \\ a_2=2^2=4 & 2 \text{ is not a multiple of }3 \text{ . Use }n^2. \\ a_3=\dfrac{3}{3}=1 & 3 \text{ is a multiple of }3 \text{. Use }\dfrac{n}{3}. \\ a_4=4^2=16 & 4 \text{ is not a multiple of }3. \text{ Use }n^2. \\ a_5=5^2=25 & 5 \text{ is not a multiple of } 3. \text{Use }n^2. \\ a_6=\dfrac{6}{3}=2 & 6 \text{ is a multiple of }3. \text{Use }\dfrac{n}{3} \end{array}$

Los primeros seis términos son$\{1, 4, 1, 16, 25, 2\}$.

Análisis

Cada tercer punto de la gráfica que se muestra en la Figura$\PageIndex{4}$ destaca de los dos puntos cercanos. Esto ocurre porque la secuencia fue definida por una función por partes.

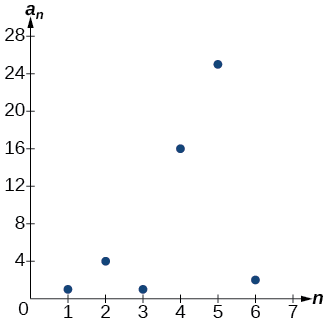
$Gráfica de una gráfica dispersa donde el eje x se etiqueta n y el eje y se etiqueta a_n.$

Figura$\PageIndex{4}$

Ejercicio$\PageIndex{3}$

Escribe los primeros seis términos de la secuencia.

$a_n=\begin{cases}2n^3 \text{ if } n\text{ is odd} \\ \dfrac{5n}{2} \text{ if } n \text{ is even}\end{cases}$

Contestar: Los primeros seis términos son$\{2, 5, 54, 10, 250, 15\}$.

Encontrar una fórmula explícita

Hasta el momento, se nos ha dado la fórmula explícita y se nos ha pedido encontrar una serie de términos de la secuencia. En ocasiones, no se da la fórmula explícita para el enésimo término de una secuencia. En cambio, se nos dan varios términos de la secuencia. Cuando esto sucede, podemos trabajar a la inversa para encontrar una fórmula explícita a partir de los primeros términos de una secuencia. La clave para encontrar una fórmula explícita es buscar un patrón en los términos. Tenga en cuenta que el patrón puede implicar términos alternos, fórmulas para numeradores, fórmulas para denominadores, exponentes o bases.

Cómo: Dados los primeros términos de una secuencia, encontrar una fórmula explícita para la secuencia

Busca un patrón entre los términos.
Si los términos son fracciones, busque un patrón separado entre los numeradores y denominadores.
Busca un patrón entre los signos de los términos.
Escribe una fórmula para$a_n$ en términos de$n$. Pon a prueba tu fórmula para$n=1$$n=2$,, y$n=3$.

Ejemplo$\PageIndex{4}$: Writing an Explicit Formula for the nth Term of a Sequence

Escribe una fórmula explícita para el enésimo término de cada secuencia.

$\{−\dfrac{2}{11}, \dfrac{3}{13}, −\dfrac{4}{15}, \dfrac{5}{17}, −\dfrac{6}{19},…\}$
$\{−\dfrac{2}{25}, −\dfrac{2}{125}, −\dfrac{2}{625}, −\dfrac{2}{3,125}, −\dfrac{2}{15,625},…\}$
$\{e^4,e^5,e^6,e^7,e^8,…\}$

Solución

Busca el patrón en cada secuencia.

Los términos alternan entre positivo y negativo. Podemos utilizar${(−1)}^n$ para hacer alternar los términos. El numerador puede ser representado por$n+1$. El denominador puede ser representado por$2n+9$.
$a_n=\dfrac{{(−1)}^n(n+1)}{2n+9}$
Los términos son todos negativos.
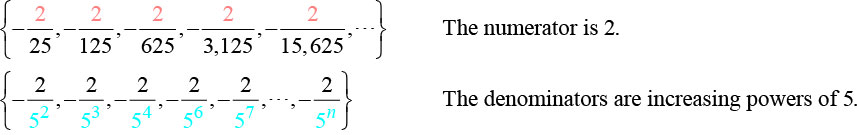
Entonces sabemos que la fracción es negativa, el numerador es$2$, y el denominador puede ser representado por$5n+1$.

$a_n=−\dfrac{2}{5^{n+1}}$
Los términos son poderes de$e$. Porque$n=1$, el primer término es$e^4$ así el exponente debe ser$n+3$.
$a_n=e^{n+3}$

Ejercicio$\PageIndex{4A}$

Escribe una fórmula explícita para el enésimo término de la secuencia.

$\{9,−81,729,−6,561,59,049,…\}$

Contestar: $a_n={(−1)}^{n+1}9^n$

Ejercicio$\PageIndex{4B}$

Escribe una fórmula explícita para el enésimo término de la secuencia.

$\{−34,−98,−2712,−8116,−24320,...\}$

Contestar: $a_n=−\dfrac{3^n}{4n}$

Ejercicio$\PageIndex{4C}$

Escribe una fórmula explícita para el enésimo término de la secuencia.

$\left \{ \dfrac{1}{e^2}, \dfrac{1}{e}, 1, e, e^2,... \right \}$

Contestar: $a_n=e^{n−3}$

Escribir los términos de una secuencia definida por una fórmula recursiva

Las secuencias ocurren naturalmente en los patrones de crecimiento de conchas de nautilus, piñas, ramas de árboles y muchas otras estructuras naturales. Podemos ver la secuencia en el arreglo de hojas o ramas, el número de pétalos de una flor o el patrón de las cámaras en una concha de nautilus. Su crecimiento sigue la secuencia de Fibonacci, una secuencia famosa en la que cada término se puede encontrar añadiendo los dos términos anteriores. Los números en la secuencia son$1, 1, 2, 3, 5, 8, 13, 21, 34,….$ Otros ejemplos del mundo natural que exhiben la secuencia de Fibonacci son el Calla Lily, que tiene solo un pétalo, la Susan de ojos negros con$13$ pétalos, y diferentes variedades de margaritas que pueden tener$21$ o$34$ pétalos.

Cada término de la secuencia de Fibonacci depende de los términos que le precedan. La secuencia de Fibonacci no se puede escribir fácilmente usando una fórmula explícita. En cambio, describimos la secuencia usando una fórmula recursiva, una fórmula que define los términos de una secuencia usando términos anteriores.

Una fórmula recursiva siempre tiene dos partes: el valor de un término inicial (o términos), y una ecuación que define$a_n$ en términos de términos anteriores. Por ejemplo, supongamos que conocemos lo siguiente:

\[\begin{align*} a_1 &= 3 \\ a_n &= 2a_{n−1}−1 , \text{ for }n≥2 \end{align*}\]

Podemos encontrar los términos posteriores de la secuencia usando el primer término.

\[\begin{align*} a_1 &= 3 \\ a_2 &= 2a_1−1=2(3)−1=5 \\ a_3 &= 2a_2−1=2(5)−1=9 \\ a_4 &= 2a_3−1=2(9)−1=17 \end{align*}\]

Entonces los primeros cuatro términos de la secuencia son$\{3, 5, 9, 17\}$.

La fórmula recursiva para la secuencia de Fibonacci establece los dos primeros términos y define cada término sucesivo como la suma de los dos términos anteriores.

\[\begin{align*}a_1 &= 1 \\ a_2 &= 1 \\ a_n &= a_{n−1}+a_{n−2} \text{, for }n≥3 \end{align*}\]

Para encontrar el décimo término de la secuencia, por ejemplo, necesitaríamos agregar los términos octavo y noveno. Nos dijeron anteriormente que los términos octavo y noveno son$21$ y$34$, entonces

$a_{10}=a_9+a_8=34+21=55$

Fórmula Recursiva

Una fórmula recursiva es una fórmula que define cada término de una secuencia usando término (s) anterior (s). Las fórmulas recursivas deben indicar siempre el término inicial, o términos, de la secuencia.

Q&A: ¿Deben darse siempre los dos primeros términos en una fórmula recursiva?

No. La secuencia de Fibonacci define cada término usando los dos términos anteriores, pero muchas fórmulas recursivas definen cada término usando solo un término precedente. Estas secuencias solo necesitan definir el primer término.

Cómo: Dada una fórmula recursiva con solo el primer término proporcionado, escribir los primeros n términos de una secuencia

Identificar el término inicial$a_1$,, que se da como parte de la fórmula. Este es el primer término.
Para encontrar el segundo término,$a_2$, sustituir el término inicial en la fórmula para$a_{n−1}$. Resolver.
Para encontrar el tercer término,$a_3$, sustituir el segundo término en la fórmula. Resolver.
Repita hasta que haya resuelto para el enésimo término.

Ejemplo$\PageIndex{5}$: Writing the Terms of a Sequence Defined by a Recursive Formula

Escribe los primeros cinco términos de la secuencia definida por la fórmula recursiva.

\[\begin{align*}a_1 &= 9 \\ a_n &= 3a_{n−1}−20 , \text{ for }n≥2 \end{align*}\]

Solución

El primer término se da en la fórmula. Para cada término posterior,$a_n−1$ sustituimos por el valor del término anterior.

$\begin{array}{ll} n=1 & a_1=9 \\ n=2 & a_2=3a_1−20=3(9)−20=27−20=7 \\ n=3 & a_3=3a_2−20=3(7)−20=21−20=1 \\ n=4 & a_4=3a_3−20=3(1)−20=3−20=−17 \\ n=5 & a_5=3a_4−20=3(−17)−20=−51−20=−71 \end{array}$

Los primeros cinco términos son$\{9, 7, 1, –17, –71\}$. Ver Figura$\PageIndex{5}$.

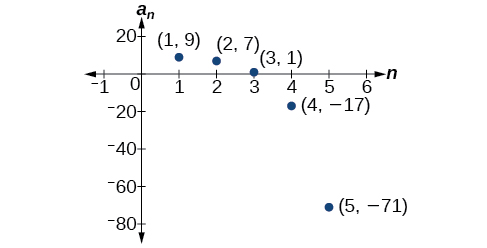
$Gráfica de una parcela dispersa con puntos etiquetados: (1, 9), (2, 7), (3, 1), (4, -17) y (5, -71). El eje x se etiqueta n y el eje y se etiqueta como a_n.$

Figura$\PageIndex{5}$

Ejercicio$\PageIndex{5}$

Escribe los primeros cinco términos de la secuencia definida por la fórmula recursiva.

\[\begin{align*} a_1 &= 2 \\ a_n &= 2a_{n−1}+1 , \text{ for }n≥2 \end{align*}\]

Contestar: $\{2, 5, 11, 23, 47\}$

Cómo: Dada una fórmula recursiva con dos términos iniciales, escribir el primero$n$ terms of a sequence

Identificar el término inicial$a_1$,, que se da como parte de la fórmula.
Identificar el segundo término$a_2$,, que se da como parte de la fórmula.
Para encontrar el tercer término, sustituya el término inicial y el segundo término en la fórmula. Evaluar.
Repita hasta que haya evaluado el enésimo término.

Ejemplo$\PageIndex{6}$: Writing the Terms of a Sequence Defined by a Recursive Formula

Escribe los primeros seis términos de la secuencia definida por la fórmula recursiva.

\[\begin{align*} a_1 &=1 \\ a_2 &= 2 \\ a_n &= 3a_{n−1}+4a_{n−2} , \text{ for }n≥3 \end{align*}\]

Solución

Se dan los dos primeros términos. Para cada término posterior, reemplazamos$a_{n−1}$ y$a_{n−2}$ con los valores de los dos términos anteriores.

$\begin{array}{ll} n=3 & a_3=3a_2+4a_1=3(2)+4(1)=10 \\ n=4 & a_4=3a_3+4a_2=3(10)+4(2)=38 \\ n=5 & a_5=3a_4+4a_3=3(38)+4(10)=154 \\ n=6 & a_6=3a_5+4a_4=3(154)+4(38)=614 \end{array}$

Los primeros seis términos son$\{1,2,10,38,154,614\}$. Ver Figura$\PageIndex{6}$.

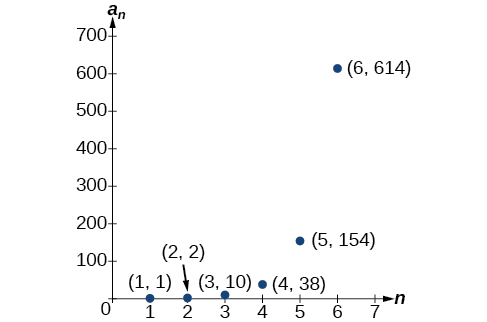
$Gráfica de una parcela dispersa con puntos etiquetados: (1, 1), (2, 2), (3, 10), (4, 38), (5, 154) y (6, 614). El eje x se etiqueta n y el eje y se etiqueta como a_n.$

Figura$\PageIndex{6}$

Ejercicio$\PageIndex{6}$

Escribe los primeros$8$ términos de la secuencia definida por la fórmula recursiva.

\[\begin{align*}a_1 &= 0 \\ a_2 &= 1 \\ a_3 &= 1 \\ a_n &= \dfrac{a_{n−1}}{a_{n−2}}+a_{n−3} , \text{ for }n≥4 \end{align*}\]

Contestar: $\left \{0, 1, 1, 1, 2, 3, 52, 176 \right \}$.

Uso de la notación factorial

Las fórmulas para algunas secuencias incluyen productos de enteros positivos consecutivos. $n$factorial, escrito como$n!$, es el producto de los enteros positivos de$1$ a$n$. Por ejemplo,

\[\begin{align*}4! &= 4⋅3⋅2⋅1=24 \\ 5! &= 5⋅4⋅3⋅2⋅1=120 \end{align*}\]

Un ejemplo de fórmula que contiene un factorial es$a_n=(n+1)!$. El sexto término de la secuencia se puede encontrar sustituyendo$6$ por$n$.

$a_6=(6+1)!=7!=7·6·5·4·3·2·1=5040$

El factorial de cualquier número entero$n$ es Por lo tanto, también$n(n−1)!$ podemos pensar en$5!$ como$5⋅4!$.

FACTORIALES

$n$factorial es una operación matemática que se puede definir mediante una fórmula recursiva. El factorial de$n$, denotado$n!$, se define para un entero positivo$n$ como:

\[\begin{align} 0! &= 1 \\ 1! &= 1 \\ n! &= n(n−1)(n−2)⋯(2)(1), \text{ for }n≥2 \end{align}\]

El caso especial$0!$ se define como$0!=1$.

Q&A: ¿Siempre se pueden encontrar factoriales usando una calculadora?

No. Las factoriales se vuelven grandes muy rápidamente, ¡más rápido que incluso las funciones exponenciales! Cuando la salida sea demasiado grande para la calculadora, no podrá calcular el factorial.

Ejemplo$\PageIndex{7}$: Writing the Terms of a Sequence Using Factorials

Escribe los primeros cinco términos de la secuencia definida por la fórmula explícita$a_n=\dfrac{5n}{(n+2)!}$.

Solución

Sustituir$n=1$$n=2$,, y así sucesivamente en la fórmula.

$\begin{array}{ll} n=1 & a_1=\dfrac{5(1)}{(1+2)!}=\dfrac{5}{3!}=\dfrac{5}{3·2·1}=\dfrac{5}{6} \\ n=2 & a_2=\dfrac{5(2)}{(2+2)!}=\dfrac{10}{4!}=\dfrac{10}{4·3·2·1}=\dfrac{5}{12} \\ n=3 & a_3=\dfrac{5(3)}{(3+2)!}=\dfrac{15}{5!}=\dfrac{15}{5·4·3·2·1}=\dfrac{1}{8} \\ n=4 & a_4=\dfrac{5(4)}{(4+2)!}=\dfrac{20}{6!}=\dfrac{20}{6·5·4·3·2·1}=\dfrac{1}{36} \\ n=5 & a_5=\dfrac{5(5)}{(5+2)!}=\dfrac{25}{7!}=\dfrac{25}{7·6·5·4·3·2·1}=\dfrac{5}{1,008} \end{array}$

Los primeros cinco términos son$\left \{\dfrac{5}{6}, \dfrac{5}{12}, \dfrac{1}{8}, \dfrac{1}{36}, \dfrac{5}{1,008} \right \}$.

Análisis

En la figura se$\PageIndex{7}$ muestra la gráfica de la secuencia. Observe que, dado que los factoriales crecen muy rápidamente, la presencia del término factorial en el denominador da como resultado que el denominador sea mucho mayor que el numerador a medida que nn aumenta. Esto significa que el cociente se hace más pequeño y, como muestra la gráfica de los términos, los términos están disminuyendo y acercándose a cero.

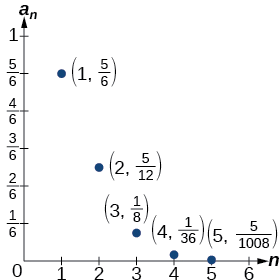
$13.2.7.pngGráfico de una parcela dispersa con puntos etiquetados: (1, 5/6), (2, 5/12), (3, 1/8), (4, 1/36) y (5, 5/1008). El eje x se etiqueta n y el eje y se etiqueta como a_n.$

Figura$\PageIndex{7}$

Ejercicio$\PageIndex{7}$

Escribe los primeros cinco términos de la secuencia definida por la fórmula explícita$a_n=\dfrac{(n+1)!}{2n}$.

Contestar: Los primeros cinco términos son$\left \{1, \dfrac{3}{2}, 4, 15, 72 \right \}$.

Medios

Acceda a este recurso en línea para obtener instrucción adicional y práctica con secuencias.

Encontrar términos en una secuencia

Ecuaciones Clave

Fórmula para un factorial

$0!=1$

$1!=1$

$n!=n(n−1)(n−2)⋯(2)(1)$, para$n≥2$

Conceptos clave

Una secuencia es una lista de números, llamados términos, escritos en un orden específico.
Las fórmulas explícitas definen cada término de una secuencia usando la posición del término. Ver Ejemplo$\PageIndex{1}$$\PageIndex{2}$, Ejemplo y Ejemplo$\PageIndex{3}$.
Una fórmula explícita para el décimo enésimo término de una secuencia se puede escribir analizando el patrón de varios términos. Ver Ejemplo$\PageIndex{4}$.
Las fórmulas recursivas definen cada término de una secuencia usando términos anteriores.
Las fórmulas recursivas deben indicar el término inicial, o términos, de una secuencia.
Un conjunto de términos se puede escribir usando una fórmula recursiva. Ver Ejemplo$\PageIndex{5}$ y Ejemplo$\PageIndex{6}$.
Un factorial es una operación matemática que se puede definir recursivamente.
El factorial de$n$ es el producto de todos los enteros desde$1$ hasta$n$. Ver Ejemplo$\PageIndex{7}$.

Colaboradores y Atribuciones

Template:ContribOpenStaxPreCalc

\(n\)	1	2	3	4	5	\(n\)
\(n^{th}\)término de la secuencia,\(a_n\)	2	4	8	16	32	\(2^n\)

Search

SECUENCIA

Q&A: ¿Una secuencia siempre tiene que empezar por\(a_1\)?

Cómo: Dada una fórmula explícita, escribir la primera\(n\) terms of a sequence

Ejemplo\(\PageIndex{1}\): Writing the Terms of a Sequence Defined by an Explicit Formula

Ejercicio\(\PageIndex{1}\)

Cómo: Dada una fórmula explícita con términos alternos, escribir los primeros términos nn de una secuencia

Ejemplo\(\PageIndex{2}\): Writing the Terms of an Alternating Sequence Defined by an Explicit Formula

Ejercicio\(\PageIndex{2}\)

Cómo: Dada una fórmula explícita para una función por partes, escriba la primera\(n\) terms of a sequence

Ejemplo\(\PageIndex{3}\): Writing the Terms of a Sequence Defined by a Piecewise Explicit Formula

Ejercicio\(\PageIndex{3}\)

Cómo: Dados los primeros términos de una secuencia, encontrar una fórmula explícita para la secuencia

Ejemplo\(\PageIndex{4}\): Writing an Explicit Formula for the nth Term of a Sequence

Ejercicio\(\PageIndex{4A}\)

Ejercicio\(\PageIndex{4B}\)

Ejercicio\(\PageIndex{4C}\)

Fórmula Recursiva

Q&A: ¿Deben darse siempre los dos primeros términos en una fórmula recursiva?

Ejemplo\(\PageIndex{5}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Ejercicio\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Ejercicio\(\PageIndex{6}\)

FACTORIALES

Q&A: ¿Siempre se pueden encontrar factoriales usando una calculadora?

Ejemplo\(\PageIndex{7}\): Writing the Terms of a Sequence Using Factorials

Ejercicio\(\PageIndex{7}\)

Objetivos de aprendizaje

Escribir los términos de una secuencia definida por una fórmula explícita

SECUENCIA

Cómo: Dada una fórmula explícita, escribir la primera\(n\) terms of a sequence

Ejemplo\(\PageIndex{1}\): Writing the Terms of a Sequence Defined by an Explicit Formula

Ejercicio\(\PageIndex{1}\)

Investigación de secuencias alternas

Cómo: Dada una fórmula explícita con términos alternos, escribir los primeros términos nn de una secuencia

Ejemplo\(\PageIndex{2}\): Writing the Terms of an Alternating Sequence Defined by an Explicit Formula

Q&A: En el ejemplo anterior, ¿el\((–1)\) to the power of \(n\) account for the oscillations of signs?

Ejercicio\(\PageIndex{2}\)

Investigando fórmulas explícitas por partes

Cómo: Dada una fórmula explícita para una función por partes, escriba la primera\(n\) terms of a sequence

Ejemplo\(\PageIndex{3}\): Writing the Terms of a Sequence Defined by a Piecewise Explicit Formula

Ejercicio\(\PageIndex{3}\)

Encontrar una fórmula explícita

Cómo: Dados los primeros términos de una secuencia, encontrar una fórmula explícita para la secuencia

Ejemplo\(\PageIndex{4}\): Writing an Explicit Formula for the nth Term of a Sequence

Ejercicio\(\PageIndex{4A}\)

Ejercicio\(\PageIndex{4B}\)

Ejercicio\(\PageIndex{4C}\)

Escribir los términos de una secuencia definida por una fórmula recursiva

Cómo: Dada una fórmula recursiva con solo el primer término proporcionado, escribir los primeros n términos de una secuencia

Ejemplo\(\PageIndex{5}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Ejercicio\(\PageIndex{5}\)

Cómo: Dada una fórmula recursiva con dos términos iniciales, escribir el primero\(n\) terms of a sequence

Ejemplo\(\PageIndex{6}\): Writing the Terms of a Sequence Defined by a Recursive Formula

Ejercicio\(\PageIndex{6}\)

Uso de la notación factorial

FACTORIALES

Ejemplo\(\PageIndex{7}\): Writing the Terms of a Sequence Using Factorials

Ejercicio\(\PageIndex{7}\)

Medios

Ecuaciones Clave

Conceptos clave

Colaboradores y Atribuciones