11.5: Principios de conteo
- Page ID
- 121378
- Resolver problemas de conteo usando el Principio de Adición.
- Resolver problemas de conteo usando el Principio de Multiplicación.
- Resolver problemas de conteo usando permutaciones que involucran n objetos distintos.
- Resuelve problemas de conteo usando combinaciones.
- Encuentra el número de subconjuntos de un conjunto dado.
- Resolver problemas de conteo usando permutaciones que involucran n objetos no distintos.
Una nueva compañía vende estuches personalizables para tabletas y smartphones. Cada estuche viene en una variedad de colores y se puede personalizar por un cargo adicional con imágenes o un monograma. Un cliente puede optar por no personalizar o podría optar por tener una, dos o tres imágenes o un monograma. El cliente puede elegir el orden de las imágenes y las letras en el monograma. La compañía está trabajando con una agencia para desarrollar una campaña de marketing con un enfoque en la gran cantidad de opciones que ofrecen. ¡Contar las posibilidades es un reto!
Nos encontramos con una amplia variedad de problemas de conteo todos los días. Existe una rama de las matemáticas dedicada al estudio de problemas de conteo como éste. Otras aplicaciones de conteo incluyen contraseñas seguras, resultados de carreras de caballos y opciones de programación universitaria. Examinaremos este tipo de matemáticas en esta sección.
Uso del principio de adición
La empresa que vende estuches personalizables ofrece estuches para tablets y smartphones. Hay modelos de tabletas\(3\) compatibles y modelos de teléfonos inteligentes\(5\) compatibles. El Principio de Adición nos dice que podemos agregar el número de opciones de tableta al número de opciones de teléfonos inteligentes para encontrar el número total de opciones. Por el Principio de Adición, hay opciones\(8\) totales, como podemos ver en la Figura\(\PageIndex{1}\).
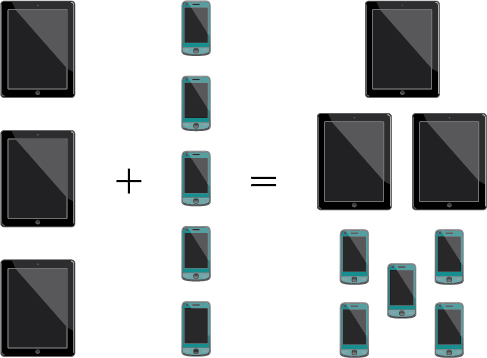
Figura\(\PageIndex{1}\)
De acuerdo con el Principio de Adición, si un evento puede ocurrir de\(m\) maneras y un segundo evento sin resultados comunes puede ocurrir de\(n\) maneras, entonces el primer o segundo evento puede ocurrir de\(m+n\) maneras.
Hay opciones de\(2\) platos vegetarianos y platos de\(5\) carne en el menú de la cena. ¿Cuál es el número total de opciones de entrada?
Solución
Podemos agregar el número de opciones vegetarianas al número de opciones de carne para encontrar el número total de opciones de plato principal.

Hay opciones\(7\) totales.
Un estudiante está comprando una nueva computadora. Está decidiendo entre computadoras\(3\) de escritorio y computadoras\(4\) portátiles. ¿Cuál es el número total de opciones de computadora?
- Contestar
-
\(7\)
Uso del principio de multiplicación
El Principio de Multiplicación se aplica cuando estamos haciendo más de una selección. Supongamos que estamos eligiendo un aperitivo, un plato principal y un postre. Si hay opciones de\(2\) aperitivo, opciones de\(3\) entrada y opciones de\(2\) postre en un menú de cena de precio fijo, hay un total de opciones\(12\) posibles de una cada una como se muestra en el diagrama de árbol de la Figura\(\PageIndex{2}\).
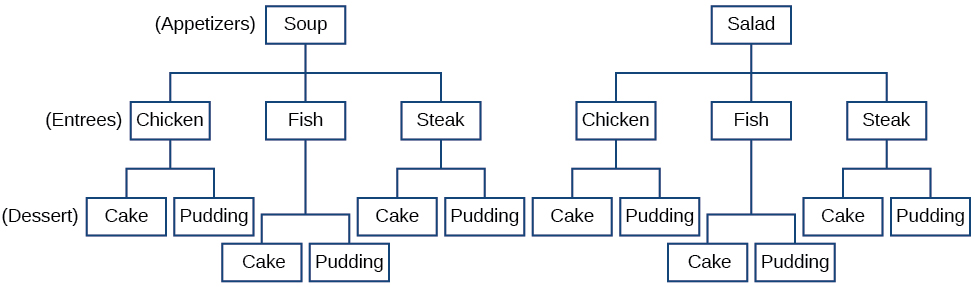
Figura\(\PageIndex{2}\)
Las opciones posibles son:
- sopa, pollo, pastel
- sopa, pollo, pudín
- sopa, pescado, pastel
- sopa, pescado, pudín
- sopa, bistec, pastel
- sopa, bistec, pudín
- ensalada, pollo, pastel
- ensalada, pollo, pudín
- ensalada, pescado, pastel
- ensalada, pescado, pudín
- ensalada, bistec, pastel
- ensalada, bistec, pudín También podemos encontrar el número total de cenas posibles multiplicando.
También podríamos concluir que hay\(12\) posibles opciones para cenar simplemente aplicando el Principio de Multiplicación.
\(\# \text{of appetizer options} \times \# \text {of entree options} \times \# \text {of dessert options}\)
\(2 × 3 × 2=12\)
De acuerdo con el Principio de Multiplicación, si un evento puede ocurrir de\(m\) maneras y un segundo evento puede ocurrir de\(n\) maneras después de que haya ocurrido el primer evento, entonces los dos eventos pueden ocurrir de\(m×n\) maneras. Esto también se conoce como el Principio Fundamental de Conteo.
Diane empacó\(2\) faldas,\(4\) blusas y un suéter para su viaje de negocios. Tendrá que elegir una falda y una blusa para cada atuendo y decidir si usar el jersey. Usa el Principio de Multiplicación para encontrar el número total de atuendos posibles.
Solución
Para encontrar el número total de atuendos, encuentra el producto del número de opciones de falda, el número de opciones de blusa y el número de opciones de suéter.

Hay\(16\) posibles atuendos.
Un restaurante ofrece un desayuno especial que incluye un sándwich de desayuno, una guarnición y una bebida. Hay\(3\) tipos de sándwiches de desayuno, opciones de\(4\) guarnición y opciones de\(5\) bebidas. Encuentra el número total de posibles ofertas especiales de desayuno.
- Contestar
-
Hay\(60\) posibles especialidades de desayuno.
Encontrar el número de permutaciones de objetos\(n\) distintos
El Principio de Multiplicación se puede utilizar para resolver una variedad de tipos de problemas. Un tipo de problema consiste en colocar objetos en orden. Organizamos letras en palabras y dígitos en números, alineamos para fotografías, decoramos habitaciones y más. Un orden de objetos se llama permutación.
Encontrar el número de permutaciones de objetos\(n\) distintos usando el principio de multiplicación
Para resolver problemas de permutación, a menudo es útil dibujar segmentos de línea para cada opción. Eso nos permite determinar el número de cada opción para que podamos multiplicar. Por ejemplo, supongamos que tenemos cuatro pinturas, y queremos encontrar la cantidad de formas en las que podemos colgar tres de las pinturas en orden en la pared. Podemos dibujar tres líneas para representar los tres lugares en la pared.

Hay cuatro opciones para el primer lugar, así que escribimos una\(4\) en la primera línea.

Después de que se haya llenado el primer lugar, hay tres opciones para el segundo lugar así que escribimos una\(3\) en la segunda línea.
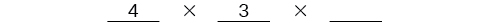
Después de que se haya llenado el segundo lugar, hay dos opciones para el tercer lugar así que escribimos una\(2\) en la tercera línea. Por último, encontramos el producto.
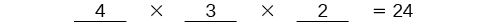
Existen\(24\) posibles permutaciones de las pinturas.
- Determinar cuántas opciones hay para la primera situación.
- Determinar cuántas opciones quedan para la segunda situación.
- Continuar hasta que se llenen todas las manchas.
- Multiplique los números juntos.
En una competencia de natación, nueve nadadores compiten en una carrera.
- ¿De cuántas maneras pueden colocar primero, segundo y tercero?
- ¿De cuántas maneras pueden colocar primero, segundo y tercero si un nadador llamado Ariel gana el primer lugar? (Supongamos que solo hay un concursante llamado Ariel.)
- ¿De cuántas maneras pueden hacer fila los nueve nadadores para una foto?
Solución
- Dibuja líneas para cada lugar.

Hay\(9\) opciones para el primer lugar. Una vez que alguien ha ganado el primer lugar,\(8\) quedan opciones para el segundo lugar. Una vez que se han ganado el primer y segundo lugar,\(7\) quedan opciones para el tercer lugar.
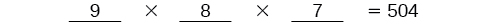
Multiplicar para encontrar que hay\(504\) formas para que los nadadores coloquen.
- Dibuja líneas para describir cada lugar.
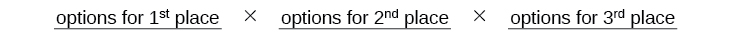
Sabemos que Ariel debe ganar el primer lugar, por lo que sólo hay\(1\) opción para el primer lugar. \(8\)Quedan opciones para el segundo lugar, y luego opciones\(7\) restantes para el tercer lugar.
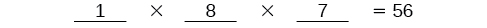
Multiplicar para encontrar que hay\(56\) formas para que los nadadores se coloquen si Ariel gana primero.
- Dibuja líneas para describir cada lugar de la foto.

Hay\(9\) opciones para el primer lugar, luego\(8\) para el segundo,\(7\) para el tercero,\(6\) para el cuarto, y así sucesivamente hasta que solo queda\(1\) persona para el último lugar.
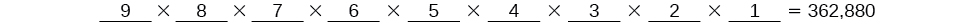
Existen\(362,880\) posibles permutaciones para que los nadadores se alineen.
Análisis
Tenga en cuenta que en la parte c, encontramos que había\(9!\) formas para que\(9\) las personas se alinearan. El número de permutaciones de objetos\(n\) distintos siempre se puede encontrar por\(n!\).
Una familia de cinco está teniendo retratos tomados. Usa el Principio de Multiplicación para encontrar lo siguiente:
- ¿De cuántas maneras puede la familia alinearse para el retrato?
- ¿De cuántas maneras puede el fotógrafo alinear a miembros de\(3\) la familia?
- ¿De cuántas maneras puede la familia alinearse para el retrato si se requiere que los padres se paren en cada extremo?
- Contestar a
-
\(120\)
- Respuesta b
-
\(60\)
- Respuesta c
-
\(12\)
Encontrar el número de permutaciones de n objetos distintos usando una fórmula
Para algunos problemas de permutación, es inconveniente usar el Principio de Multiplicación porque hay tantos números para multiplicar. Afortunadamente, podemos resolver estos problemas usando una fórmula. Antes de aprender la fórmula, veamos dos notaciones comunes para las permutaciones. Si tenemos un conjunto de\(n\) objetos y queremos elegir\(r\) objetos del conjunto en orden, escribimos\(P(n,r)\). Otra forma de escribir esto es\(nP_r\), una notación comúnmente vista en computadoras y calculadoras. Para calcular\(P(n,r)\), comenzamos por encontrar\(n!\), el número de formas de alinear todos los objetos nn. Luego dividimos por\((n−r)!\) para cancelar los\((n−r)\) artículos que no deseamos alinear.
Veamos cómo funciona esto con un ejemplo sencillo. Imagina un club de seis personas. Necesitan elegir un presidente, un vicepresidente y un tesorero. Seis personas pueden ser electas presidente, cualquiera de las cinco personas restantes puede ser electo vicepresidente, y cualquiera de las cuatro personas restantes podría ser electo tesorero. El número de formas en que esto se puede hacer es\(6×5×4=120\). Usando factoriales, obtenemos el mismo resultado.
\(\dfrac{6!}{3!}=\dfrac{6·5·4·3!}{3!}=6·5·4=120 \)
Hay\(120\) formas de seleccionar\(3\) oficiales en orden de un club con\(6\) miembros. Nos referimos a esto como una permutación de\(6\) tomada\(3\) a la vez. La fórmula general es la siguiente.
\[P(n,r)=\dfrac{n!}{(n−r)!}\]
Tenga en cuenta que las imágenes fijas de fórmula funcionan si estamos eligiendo todos los\(n\) objetos y colocándolos en orden. En ese caso estaríamos dividiendo por\((n−n)!\) o\(0!\), que dijimos antes es igual a\(1\). Entonces el número de permutaciones de\(n\) objetos tomados\(n\) a la vez es\(\dfrac{n!}{1}\) o simplemente\(n!\).
Dados los\(n\) distintos objetos, el número de formas de seleccionar\(r\) objetos del conjunto en orden es
\[P(n,r)=\dfrac{n!}{(n−r)!}\]
- Identificar\(n\) a partir de la información dada.
- Identificar\(r\) a partir de la información dada.
- Reemplazar\(n\) y\(r\) en la fórmula con los valores dados.
- Evaluar.
Un profesor está creando un examen de\(9\) preguntas a partir de un banco de pruebas de\(12\) preguntas. ¿De cuántas maneras puede seleccionar y arreglar las preguntas?
Solución
Sustituir\(n=12\) y\(r=9\) en la fórmula de permutación y simplificar.
\[\begin{align*} P(n,r)&=\dfrac{n!}{(n-r)!}\\ P(12,9)&=\dfrac{12!}{(12-9)!}\\ &=\dfrac{12!}{3!}\\ &=79,833,600 \end{align*}\]
¡Hay\(79,833,600\) posibles permutaciones de preguntas de examen!
Análisis
También podemos usar una calculadora para encontrar permutaciones. Para este problema, entraríamos\(12\), presionaríamos la\(nP_r\) función, enter\(9\), y luego presionaríamos el signo igual. La\(nP_r\) función puede estar ubicada bajo el menú MATH con comandos de probabilidad.
¿Podríamos haber resuelto el ejemplo anterior usando el Principio de Multiplicación?
Sí. Podríamos habernos multiplicado\(15⋅14⋅13⋅12⋅11⋅10⋅9⋅8⋅7⋅6⋅5⋅4\) para encontrar la misma respuesta.
Una obra tiene un elenco de\(7\) actores que se preparan para hacer su llamada del telón. Utilice la fórmula de permutación para encontrar lo siguiente.
¿De cuántas formas pueden alinearse los\(7\) actores?
- Contestar
-
\(P(7,7)=5,040\)
¿Cuántas formas se pueden elegir\(5\) de los\(7\) actores para alinearse?
- Contestar
-
\(P(7,5)=2,520\)
Encuentra el número de combinaciones usando la fórmula
Hasta el momento, hemos mirado los problemas que nos piden poner los objetos en orden. Son muchos los problemas en los que queremos seleccionar algunos objetos de un grupo de objetos, pero no nos importa el orden. Cuando estamos seleccionando objetos y el orden no importa, estamos tratando con combinaciones. Una selección de\(r\) objetos de un conjunto de\(n\) objetos donde el orden no importa se puede escribir como\(C(n,r)\). Al igual que con las permutaciones, también se\(C(n,r)\) puede escribir como\(nC_r\). En este caso, la fórmula general es la siguiente.
\[C(n,r)=\dfrac{n!}{r!(n−r)!} \label{combo}\]
Un problema anterior consideró\(3\) la elección de\(4\) posibles pinturas para colgar en una pared. Encontramos que había\(24\) formas\(3\) de seleccionar las\(4\) pinturas en orden. Pero, ¿y si no nos importaba la orden? Esperaríamos un número menor porque seleccionar pinturas\(1, 2, 3\) sería lo mismo que seleccionar pinturas\(2, 3, 1\). Para encontrar el número de formas de seleccionar\(3\) de las\(4\) pinturas, sin tener en cuenta el orden de las pinturas, dividir el número de permutaciones por el número de formas de ordenar\(3\) pinturas. Hay\(3!=3·2·1=6\) formas de ordenar\(3\) pinturas. Hay\(\dfrac{24}{6}\), o\(4\) formas\(3\) de seleccionar de las\(4\) pinturas. Este número tiene sentido porque cada vez que estamos seleccionando\(3\) pinturas, no estamos seleccionando\(1\) pintura. Hay\(4\) pinturas que podríamos elegir no seleccionar, así que hay\(4\) formas\(3\) de seleccionar de las\(4\) pinturas.
Dados los\(n\) distintos objetos, el número de formas de seleccionar\(r\) objetos del conjunto es
\[C(n,r)=\dfrac{n!}{r!(n−r)!}\]
- Identificar\(n\) a partir de la información dada.
- Identificar\(r\) a partir de la información dada.
- Reemplazar\(n\) y\(r\) en la fórmula con los valores dados.
- Evaluar.
Un restaurante de comida rápida ofrece cinco opciones de guarnición. Tu comida viene con dos guarniciones.
- ¿De cuántas maneras puedes seleccionar tus guarniciones?
- ¿De cuántas maneras puedes seleccionar\(3\) guarniciones?
Solución
- Queremos elegir\(2\) guarniciones entre las\(5\) opciones.
\(C(5,2)=\dfrac{5!}{2!(5−2)!}=10\)
- Queremos elegir\(3\) guarniciones entre las\(5\) opciones.
\(C(5,3)=\dfrac{5!}{3!(5−3)!}=10\)
Análisis
También podemos usar una calculadora gráfica para encontrar combinaciones. Ingrese 5, luego presione\(nC_r\), ingrese 3 y luego presione el signo igual. La función\(nC_r\), puede estar ubicada bajo el menú MATH con comandos de probabilidad.
¿Es una coincidencia que las partes (a) y (b) del ejemplo anterior tengan las mismas respuestas?
No. Cuando elegimos r objetos de n objetos, no estamos eligiendo\((n–r)\) objetos. Por lo tanto,\(C(n,r)=C(n,n–r)\).
Una heladería ofrece\(10\) sabores de helado. ¿Cuántas formas hay de elegir\(3\) sabores para un split de plátano?
- Contestar
-
\(C(10,3)=120\)
Encontrar el número de subconjuntos de un conjunto
Solo hemos mirado problemas de combinación en los que elegimos exactamente rr objetos. En algunos problemas, queremos considerar elegir cada número posible de objetos. Considera, por ejemplo, una pizzería que ofrezca\(5\) coberturas. Se puede pedir cualquier número de coberturas. ¿Cuántas pizzas diferentes son posibles?
Para responder a esta pregunta, necesitamos considerar pizzas con cualquier cantidad de coberturas. Hay\(C(5,0)=1\) manera de pedir una pizza sin coberturas. Hay\(C(5,1)=5\) formas de pedir una pizza con exactamente una cobertura. Si continuamos con este proceso, obtenemos
\(C(5,0)+C(5,1)+C(5,2)+C(5,3)+C(5,4)+C(5,5)=32\)
Hay\(32\) posibles pizzas. Este resultado es igual a\(2^5\).
Se nos presenta una secuencia de elecciones. Para cada uno de los objetos nn tenemos dos opciones: incluirlo en el subconjunto o no. Entonces, para todo el subconjunto hemos hecho nn elecciones, cada una con dos opciones. Entonces hay un total de\(2·2·2·…·2\) posibles subconjuntos resultantes, todo el camino desde el subconjunto vacío, que obtenemos cuando decimos “no” cada vez, hasta el conjunto original mismo, que obtenemos cuando decimos “sí” cada vez.
Un conjunto que contiene n objetos distintos tiene\(2^n\) subconjuntos.
Un restaurante ofrece mantequilla, queso, cebollín y crema agria como aderezos para una papa horneada. ¿Cuántas formas diferentes hay de pedir una papa?
Solución
Estamos buscando el número de subconjuntos de un conjunto con\(4\) objetos. Sustituir\(n=4\) en la fórmula.
\[\begin{align*} 2^n&=2^4\\ &=16 \end{align*}\]
Hay formas\(16\) posibles de pedir una papa.
Un bar de helados en una boda tiene\(6\) coberturas para elegir. Se puede elegir cualquier número de coberturas. ¿Cuántos sundaes diferentes son posibles?
- Contestar
-
\(64\)sundaes
Encontrar el número de permutaciones de n objetos no distintos
Hemos estudiado permutaciones donde todos los objetos involucrados eran distintos. ¿Qué pasa si algunos de los objetos son indistinguibles? Por ejemplo, supongamos que hay una hoja de\(12\) pegatinas. Si todas las pegatinas fueran distintas, habría\(12!\) formas de ordenar las pegatinas. No obstante,\(4\) de las pegatinas son estrellas idénticas, y\(3\) son lunas idénticas. Debido a que todos los objetos no son distintos, muchas de las\(12!\) permutaciones que contamos son duplicadas. La fórmula general para esta situación es la siguiente.
\[\dfrac{n!}{r_1!r_2!…r_k!}\]
En este ejemplo, necesitamos dividir por el número de formas de ordenar las\(4\) estrellas y las formas de ordenar las\(3\) lunas para encontrar el número de permutaciones únicas de las pegatinas. Hay\(4!\) formas de ordenar las estrellas y\(3!\) formas de ordenar la luna.
\(\dfrac{12!}{4!3!}=3,326,400\)
Hay\(3,326,400\) formas de pedir la hoja de pegatinas.
Si hay nn elementos en un conjunto y\(r_1\) son iguales,\(r_2\) son iguales,\(r_3\) son iguales, y así sucesivamente\(r_k\), el número de permutaciones puede ser encontrado por
\[\dfrac{n!}{r_1!r_2!…r_k!}\]
Encuentra el número de reordenamientos de las letras en la palabra DISTINCT.
Solución
Hay\(8\) letras. Ambos\(I\) y\(T\) son\(2\) tiempos repetidos. Sustituir\(n=8\)\(r_1=2\),, y\(r_2=2\) en la fórmula.
\(\dfrac{8!}{2!2!}=10,080\)
Hay\(10,080\) arreglos.
Encuentra el número de reordenamientos de las letras en la palabra TRANSPORTADORA.
- Contestar
-
\(840\)
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con combinaciones y permutaciones.
Ecuaciones Clave
| número de permutaciones de\(n\) distintos objetos tomados\(r\) a la vez | \(P(n,r)=\dfrac{n!}{(n−r)!}\) |
| número de combinaciones de\(n\) distintos objetos tomados\(r\) a la vez | \(C(n,r)=\dfrac{n!}{r!(n−r)!}\) |
| número de permutaciones de objetos\(n\) no distintos | \(\dfrac{n!}{r1!r2!…rk!}\) |
Conceptos clave
- Si un evento puede ocurrir de\(m\) maneras y un segundo evento sin resultados comunes puede ocurrir de\(n\) maneras, entonces el primer o segundo evento puede ocurrir de\(m+n\) maneras. Ver Ejemplo\(\PageIndex{1}\).
- Si un evento puede ocurrir de\(m\) maneras y un segundo evento puede ocurrir de\(n\) maneras después de que se haya producido el primer evento, entonces los dos eventos pueden ocurrir de\(m×n\) maneras. Ver Ejemplo\(\PageIndex{2}\).
- Una permutación es un orden de\(n\) objetos.
- Si tenemos un conjunto de\(n\) objetos y queremos elegir\(r\) objetos del conjunto en orden, escribimos\(P(n,r)\).
- Los problemas de permutación se pueden resolver usando el Principio de Multiplicación o la fórmula para\(P(n,r)\). Ver Ejemplo\(\PageIndex{3}\) y Ejemplo\(\PageIndex{4}\).
- Una selección de objetos donde el orden no importa es una combinación.
- Dados los\(n\) distintos objetos, el número de formas de seleccionar\(r\) objetos del conjunto es\(C(n,r)\) y se puede encontrar usando una fórmula. Ver Ejemplo\(\PageIndex{5}\).
- Un conjunto que contiene objetos\(n\) distintos tiene\(2n\) subconjuntos. Ver Ejemplo\(\PageIndex{6}\).
- Para contar problemas que involucran objetos no distintos, necesitamos dividir para evitar contar permutaciones duplicadas. Ver Ejemplo\(\PageIndex{7}\).


