11.7: Probabilidad
- Page ID
- 121355
- Construir modelos de probabilidad.
- Cálculo de probabilidades de resultados igualmente probables.
- Cálculo de probabilidades de la unión de dos eventos.
- Usa la regla del complemento para encontrar probabilidades.
- Cálculo de probabilidad usando teoría de conteo.
Los residentes del sureste de Estados Unidos están muy familiarizados con las cartas, conocidas como modelos de espagueti, como la de Figure\(\PageIndex{1}\). Combinan una colección de datos meteorológicos para predecir la trayectoria más probable de un huracán. Cada línea coloreada representa un camino posible. El grupo de líneas onduladas puede comenzar a parecerse a hebras de espaguetis, de ahí el nombre. En esta sección, investigaremos métodos para hacer este tipo de predicciones.
Figura\(\PageIndex{1}\): Un ejemplo de un “modelo de espagueti”, que puede ser utilizado para predecir posibles caminos de una tormenta tropical. 1
Construyendo Modelos de Probabilidad
Supongamos que rodamos un cubo numérico de seis lados. Rodando un cubo numérico es un ejemplo de un experimento, o una actividad con un resultado observable. Los números en el cubo son posibles resultados, o resultados, de este experimento. El conjunto de todos los resultados posibles de un experimento se denomina espacio muestral del experimento. El espacio muestral para este experimento es\(\{1,2,3,4,5,6 \}\). Un evento es cualquier subconjunto de un espacio de muestra.
La probabilidad de un evento se conoce como probabilidad. La probabilidad de un evento pp es un número que siempre satisface\(0≤p≤1\), donde\(0\) indica un evento imposible e\(1\) indica un evento determinado. Un modelo de probabilidad es una descripción matemática de un experimento que enumera todos los resultados posibles y sus probabilidades asociadas. Por ejemplo, si existe la\(1\%\) posibilidad de ganar un sorteo y una\(99\%\) posibilidad de perder el sorteo, un modelo de probabilidad se parecería mucho a Table\(\PageIndex{1}\).
| Resultado | Probabilidad |
|---|---|
| Ganar la rifa | 1% |
| Perder la rifa | 99% |
La suma de las probabilidades listadas en un modelo de probabilidad debe ser igual\(1\), o\(100\%\).
- Identificar cada resultado.
- Determinar el número total de resultados posibles.
- Comparar cada resultado con el número total de resultados posibles.
Construir un modelo de probabilidad para rodar un solo dado justo, siendo el evento el número que se muestra en el dado.
Solución
Comience haciendo una lista de todos los resultados posibles para el experimento. Los posibles resultados son los números que se pueden rodar:\(1\)\(2\),\(3\),\(4\),\(5\), y\(6\). Hay seis posibles resultados que conforman el espacio muestral.
Asignar probabilidades a cada resultado en el espacio muestral determinando una relación entre el resultado y el número de resultados posibles. Hay uno de cada uno de los seis números en el cubo, y no hay razón para pensar que cualquier cara en particular tiene más probabilidades de aparecer que cualquier otra, por lo que la probabilidad de rodar cualquier número es\(16\).
| Resultado | Rollo de 1 | Rollo de 2 | Rollo de 3 | Rollo de 4 | Rollo de 5 | Rollo de 6 |
|---|---|---|---|---|---|---|
| Probabilidad | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) |
No. Las probabilidades se pueden expresar como fracciones, decimales o por ciento. La probabilidad siempre debe ser un número entre\(0\) y\(1\), inclusive de\(0\) y\(1\).
Probabilidades de cálculo de resultados igualmente probables
Dejar\(S\) ser un espacio de muestra para un experimento. Al investigar la probabilidad, un evento es cualquier subconjunto de\(S\). Cuando los resultados de un experimento son igualmente probables, podemos encontrar la probabilidad de un evento dividiendo el número de resultados en el evento por el número total de resultados en\(S\). Supongamos que se rueda un cubo numérico, y estamos interesados en encontrar la probabilidad de que el evento “ruede un número menor o igual a 4”. Hay 4 posibles resultados en el evento y 6 posibles resultados en\(S\), por lo que la probabilidad del evento es\(\dfrac{4}{6}=\dfrac{2}{3}\).
La probabilidad de un evento\(E\) en un experimento con espacio muestral\(S\) con resultados igualmente probables viene dada por
\[P(E)=\dfrac{\text{number of elements in }E}{\text{number of elements in }S}=\dfrac{n(E)}{n(S)}\]
\(E\)es un subconjunto de\(S\), por lo que siempre es cierto que\(0≤P(E)≤1\).
Se enrolla un cubo numérico. Encuentra la probabilidad de rodar un número impar.
Solución
El evento “rodando un número impar” contiene tres resultados. Hay resultados\(6\) igualmente probables en el espacio muestral. Dividir para encontrar la probabilidad del evento.
\(P(E)=\dfrac{3}{6}=\dfrac{1}{2}\)
Se enrolla un cubo numérico. Encuentra la probabilidad de rodar un número mayor que\(2\).
- Contestar
-
\(\dfrac{2}{3}\)
Computación de la Probabilidad de la Unión de Dos Eventos
A menudo nos interesa encontrar la probabilidad de que ocurra uno de los múltiples eventos. Supongamos que estamos jugando un juego de cartas, y vamos a ganar si la siguiente carta extraída es un corazón o un rey. Nos interesaría encontrar la probabilidad de que la siguiente carta sea un corazón o un rey. La unión de dos eventos\(E\) y\(F\), escrito\(E\cup F\), es el evento que ocurre si se producen uno o ambos eventos.
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Supongamos que la hiladora en la Figura\(\PageIndex{2}\) está girada Queremos encontrar la probabilidad de girar naranja o girar a\(b\).
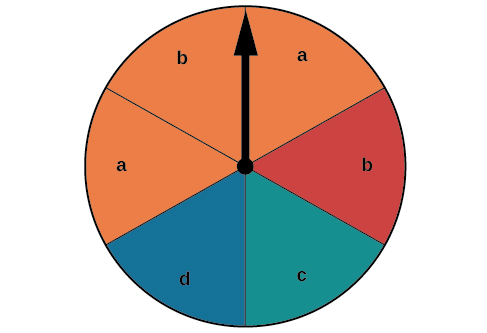
Figura\(\PageIndex{2}\): Un gráfico circular con seis opciones.
Hay un total de\(6\) secciones, y\(3\) de ellas son naranjas. Entonces la probabilidad de girar naranja es\(\dfrac{3}{6}=\dfrac{1}{2}\). Hay un total de\(6\) secciones, y\(2\) de ellas tienen un\(b\). Entonces la probabilidad de girar a\(b\) es\(\dfrac{2}{6}=\dfrac{1}{3}\). Si agregáramos estas dos probabilidades, estaríamos contando el sector que es a la vez naranja y un\(b\) dos veces. Para encontrar la probabilidad de girar una naranja o una\(b\), necesitamos restar la probabilidad de que el sector sea a la vez naranja y tenga a\(b\).
\(\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{6}=\dfrac{2}{3}\)
La probabilidad de girar naranja o a\(b\) es\(\dfrac{2}{3}\).
La probabilidad de la unión de dos eventos\(E\) y\(F\) (escrito\(E\cup F\)) es igual a la suma de la probabilidad de\(E\) y la probabilidad de\(F\) menos la probabilidad de\(E\) y\(F\) ocurrir juntos (que se llama la intersección de\(E\) y\(F\) y se escribe como\(E\cap F\)).
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Una carta es extraída de una baraja estándar. Encuentra la probabilidad de dibujar un corazón o un\(7\).
Solución
Una baraja estándar contiene el mismo número de corazones, diamantes, palos y espadas. Entonces la probabilidad de dibujar un corazón es\(\dfrac{1}{4}\). Hay cuatro\(7s\) en una baraja estándar, y hay un total de\(52\) cartas. Entonces la probabilidad de dibujar a\(7\) es\(\dfrac{1}{13}\).
La única carta en la baraja que es a la vez un corazón y a\(7\) es la\(7\) de corazones, por lo que la probabilidad de sacar tanto un corazón como una\(7\) es\(\dfrac{1}{52}\). Sustituir\(P(H)=\dfrac{1}{4}\)\(P(7)=\dfrac{1}{13}\),, y\(P(H\cap 7)=\dfrac{1}{52}\) en la fórmula.
\[\begin{align*} P(E\cup F) &=P(E)+P(F)−P(E\cap F) \\[4pt] &=\dfrac{1}{4}+\dfrac{1}{13}−\dfrac{1}{52} \\[4pt] &=\dfrac{4}{13} \end{align*}\]
La probabilidad de dibujar un corazón o un\(7\) es\(\dfrac{4}{13}\).
Una carta es extraída de una baraja estándar. Encuentra la probabilidad de sacar una tarjeta roja o un as.
- Contestar
-
\(\dfrac{7}{13}\)
Computación de la probabilidad de eventos mutuamente excluyentes
Supongamos que el spinner en Figura\(\PageIndex{2}\) vuelve a girar, pero esta vez nos interesa la probabilidad de hacer girar una naranja o una\(d\). No hay sectores que sean a la vez anaranjados y contengan a\(d\), por lo que estos dos eventos no tienen resultados en común. Se dice que los eventos son eventos mutuamente excluyentes cuando no tienen resultados en común. Porque no hay solapamiento, no hay nada que restar, entonces la fórmula general es
\[P(E\cap F)=P(E)+P(F)\]
Observe que con eventos mutuamente excluyentes, la intersección de\(E\) y\(F\) es el conjunto vacío. La probabilidad de girar una naranja es\(\dfrac{3}{6}=\dfrac{1}{2}\) y la probabilidad de girar a\(d\) es\(\dfrac{1}{6}\). Podemos encontrar la probabilidad de girar una naranja o una\(d\) simplemente sumando las dos probabilidades.
\[\begin{align*} P(E\cap F)&=P(E)+P(F) \\[4pt] &=\dfrac{1}{2}+\dfrac{1}{6} \\ &=\dfrac{2}{3} \end{align*}\]
La probabilidad de hacer girar una naranja o a\(d\) es\(\dfrac{2}{3}\).
La probabilidad de la unión de dos eventos mutuamente excluyentes\(E\) y\(F\) viene dada por
\[P(E\cap F)=P(E)+P(F)\]
- Determinar el número total de resultados para el primer evento.
- Encuentra la probabilidad del primer evento.
- Determinar el número total de resultados para el segundo evento.
- Encuentra la probabilidad del segundo evento.
- Agregar las probabilidades.
Una carta es extraída de una baraja estándar. Encuentra la probabilidad de dibujar un corazón o una pala.
Solución
Los eventos “dibujando un corazón” y “dibujando una pala” son mutuamente excluyentes porque no pueden ocurrir al mismo tiempo. La probabilidad de dibujar un corazón es\(\dfrac{1}{4}\), y la probabilidad de dibujar una pala también lo es\(\dfrac{1}{4}\), por lo que la probabilidad de dibujar un corazón o una pala es
\(\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\)
Una carta es extraída de una baraja estándar. Encuentra la probabilidad de dibujar un as o un rey.
- Contestar
-
\(\dfrac{2}{13}\)
Uso de la regla de complemento para calcular probabilidades
Hemos discutido cómo calcular la probabilidad de que ocurra un evento. En ocasiones, nos interesa encontrar la probabilidad de que un evento no suceda. El complemento de un evento\(E\), denotado\(E′\), es el conjunto de resultados en el espacio muestral que no se encuentran\(E\). Por ejemplo, supongamos que nos interesa la probabilidad de que un caballo pierda una carrera. Si evento\(W\) es el caballo ganando la carrera, entonces el complemento del evento\(W\) es el caballo perdiendo la carrera.
Para encontrar la probabilidad de que el caballo pierda la carrera, necesitamos usar el hecho de que la suma de todas las probabilidades en un modelo de probabilidad debe ser\(1\).
\[P(E′)=1−P(E)\]
La probabilidad de que el caballo gane sumada a la probabilidad de que el caballo pierda debe ser igual a\(1\). Por lo tanto, si la probabilidad de que el caballo gane la carrera es\(\dfrac{1}{9}\), la probabilidad de que el caballo pierda la carrera es simplemente
\(1−\dfrac{1}{9}=\dfrac{8}{9}\)
La probabilidad de que ocurra el complemento de un evento viene dada por
\[P(E′)=1−P(E)\]
Se enrollan dos cubos numéricos de seis lados.
- Encuentra la probabilidad de que la suma de los números rodados sea menor o igual a\(3\).
- Encuentra la probabilidad de que la suma de los números rodados sea mayor que\(3\).
Solución
El primer paso es identificar el espacio muestral, que consiste en todos los resultados posibles. Hay dos cubos numéricos, y cada cubo numérico tiene seis resultados posibles. Usando el Principio de Multiplicación, encontramos que hay\(6×6\), o\(36\) totales posibles resultados. Entonces, por ejemplo,\(1-1\) representa un\(1\) rodado en cada cubo numérico.
| \(1-1\) | \(1-2\) | \(1-3\) | \(1-4\) | \(1-5\) | \(1-6\) |
| \(2-1\) | \(2-2\) | \(2-3\) | \(2-4\) | \(2-5\) | \(2-6\) |
| \(3-1\) | \(3-2\) | \(3-3\) | \(3-4\) | \(3-5\) | \(3-6\) |
| \(4-1\) | \(4-2\) | \(4-3\) | \(4-4\) | \(4-5\) | \(4-6\) |
| \(5-1\) | \(5-2\) | \(5-3\) | \(5-4\) | \(5-5\) | \(5-6\) |
| \(6-1\) | \(6-2\) | \(6-3\) | \(6-4\) | \(6-5\) | \(6-6\) |
- Tenemos que contar el número de formas de rodar una suma de\(3\) o menos. Estos incluirían los siguientes resultados:\(1-1\),\(1-2\), y\(2-1\). Por lo que sólo hay tres formas de rodar una suma de\(3\) o menos. La probabilidad es
\(\dfrac{3}{36}=\dfrac{1}{12}\)
- En lugar de enumerar todas las posibilidades, podemos usar la Regla Complemento. Debido a que ya hemos encontrado la probabilidad del complemento de este evento, podemos simplemente restar esa probabilidad de\(1\) encontrar la probabilidad de que la suma de los números rodados sea mayor que\(3\).
\[\begin{align*} P(E')&=1-P(E)\\ &=1-\dfrac{1}{12}\\ &=\dfrac{11}{12} \end{align*}\]
Se enrollan dos cubos numéricos. Utilice la Regla Complemento para encontrar la probabilidad de que la suma sea menor que\(10\).
- Contestar
-
\(\dfrac{5}{6}\)
Computación de probabilidad usando teoría de conteo
Muchos problemas de probabilidad interesantes involucran principios de conteo, permutaciones y combinaciones. En estos problemas, utilizaremos permutaciones y combinaciones para encontrar el número de elementos en eventos y espacios de muestra. Estos problemas pueden ser complicados, pero se pueden hacer más fáciles dividiéndolos en problemas de conteo más pequeños.
Supongamos, por ejemplo, que una tienda tiene\(8\) celulares y los\(3\) de esos son defectuosos. Es posible que queramos encontrar la probabilidad de que una pareja que compra\(2\) teléfonos reciba\(2\) teléfonos que no estén defectuosos. Para resolver este problema, necesitamos calcular todas las formas de seleccionar\(2\) teléfonos que no están defectuosos, así como todas las formas de seleccionar\(2\) teléfonos. Hay\(5\) teléfonos que no están defectuosos, por lo que hay\(C(5,2)\) formas de seleccionar\(2\) teléfonos que no están defectuosos. Hay\(8\) teléfonos, por lo que hay\(C(8,2)\) formas de seleccionar\(2\) teléfonos. La probabilidad de seleccionar\(2\) teléfonos que no son defectuosos es:
\[ \begin{align*} \dfrac{\text{ways to select 2 phones that are not defective}}{\text{ways to select 2 phones}}&=\dfrac{C(5,2)}{C(8,2)} \\[4pt] &=\dfrac{10}{28} \\[4pt] &=\dfrac{5}{14} \end{align*}\]
Un niño selecciona aleatoriamente\(5\) juguetes de una papelera que contiene\(3\) conejitos,\(5\) perros y\(6\) osos.
- Encuentra la probabilidad de que solo se elijan osos.
- Encuentra la probabilidad de que se elijan\(2\) osos y\(3\) perros.
- Encuentra la probabilidad de que al menos se escojan\(2\) perros.
Solución
- Necesitamos contar el número de formas de elegir solo osos y el número total de formas posibles de seleccionar\(5\) juguetes. Hay\(6\) osos, entonces hay\(C(6,5)\) formas de elegir\(5\) osos. Hay\(14\) juguetes, así que hay\(C(14,5)\) formas de elegir cualquier\(5\) juguete.
\(\dfrac{C(6,5)}{C(14,5)}=\dfrac{6}{2,002}=\dfrac{3}{1,001}\)
- Necesitamos contar el número de formas de elegir\(2\) osos y\(3\) perros y el número total de formas posibles de seleccionar\(5\) juguetes. Hay\(6\) osos, entonces hay\(C(6,2)\) formas de elegir\(2\) osos. Hay\(5\) perros, así que hay\(C(5,3)\) formas de elegir\(3\) perros. Ya que estamos eligiendo tanto osos como perros al mismo tiempo, usaremos el Principio de Multiplicación. Hay\(C(6,2)⋅C(5,3)\) formas de elegir\(2\) osos y\(3\) perros. Podemos usar este resultado para encontrar la probabilidad.
\(\dfrac{C(6,2)C(5,3)}{C(14,5)}=\dfrac{15⋅10}{2,002}=\dfrac{75}{1,001}\)
- A menudo es más fácil resolver “al menos” problemas usando la Regla del Complemento. Comenzaremos por encontrar la probabilidad de que se escojan menos que\(2\) perros. Si se eligen menos de\(2\) perros, entonces o no se podría elegir ningún perro, o se podría elegir un\(1\) perro.
Cuando no se eligen perros, todos los\(5\) juguetes provienen de los\(9\) juguetes que no son perros. Hay\(C(9,5)\) formas de elegir juguetes de los\(9\) juguetes que no son perros. Como hay\(14\) juguetes, hay\(C(14,5)\) formas de elegir los\(5\) juguetes de todos los juguetes.
\(\dfrac{C(9,5)}{C(14,5)}=\dfrac{63}{1,001}\)
Si hay\(1\) perro elegido, entonces los\(4\) juguetes deben provenir de los\(9\) juguetes que no son perros, y\(1\) deben venir de los\(5\) perros. Ya que estamos eligiendo tanto perros como otros juguetes al mismo tiempo, usaremos el Principio de Multiplicación. Hay\(C(5,1)⋅C(9,4)\) formas de elegir\(1\) perro y\(1\) otro juguete.
\(\dfrac{C(5,1)C(9,4)}{C(14,5)}=\dfrac{5⋅126}{2,002}=\dfrac{315}{1,001}\)
Debido a que estos eventos no ocurrirían juntos y por lo tanto son mutuamente excluyentes, agregamos las probabilidades de encontrar la probabilidad de que se escojan menos que\(2\) perros.
\(\dfrac{63}{1,001}+\dfrac{315}{1,001}=\dfrac{378}{1,001}\)
Luego restamos esa probabilidad de\(1\) encontrar la probabilidad de que al menos se escojan\(2\) perros.
\(1−\dfrac{378}{1,001}=\dfrac{623}{1,001}\)
Un niño selecciona aleatoriamente las\(3\) pelotas de goma de un contenedor que contiene los gumballs\(4\) morados, los gumballs\(8\) amarillos y los gumballs\(2\) verdes.
- Encuentra la probabilidad de que todos los\(3\) gumballs seleccionados sean morados.
- Encuentra la probabilidad de que no se seleccionen gumballs amarillos.
- Encuentra la probabilidad de que se seleccione al menos gumball\(1\) amarillo.
- Contestar
-
\(\dfrac{1}{91}\)
- Contestar
-
\(\dfrac{5}{91}\)
- Contestar
-
\(\dfrac{86}{91}\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con probabilidad.
Visite este sitio web para obtener preguntas de práctica adicionales de Learningpod.
Ecuaciones Clave
| probabilidad de un evento con resultados igualmente probables | \(P(E)=\dfrac{n(E)}{n(S)}\) |
| probabilidad de la unión de dos eventos | \(P(E\cup F)=P(E)+P(F)−P(E\cap F)\) |
| probabilidad de la unión de eventos mutuamente excluyentes | \(P(E\cup F)=P(E)+P(F)\) |
| probabilidad del complemento de un evento | \(P(E')=1−P(E)\) |
Conceptos clave
- La probabilidad es siempre un número entre\(0\) y\(1\), donde\(0\) significa que un evento es imposible y\(1\) significa que un evento es cierto.
- Las probabilidades en un modelo de probabilidad deben sumar a\(1\). Ver Ejemplo\(\PageIndex{1}\).
- Cuando los resultados de un experimento son igualmente probables, podemos encontrar la probabilidad de un evento dividiendo el número de resultados en el evento por el número total de resultados en el espacio de muestra para el experimento. Ver Ejemplo\(\PageIndex{2}\).
- Para encontrar la probabilidad de la unión de dos eventos, sumamos las probabilidades de los dos eventos y restamos la probabilidad de que ambos eventos ocurran simultáneamente. Ver Ejemplo\(\PageIndex{3}\).
- Para encontrar la probabilidad de la unión de dos eventos mutuamente excluyentes, agregamos las probabilidades de cada uno de los eventos. Ver Ejemplo\(\PageIndex{4}\).
- La probabilidad del complemento de un evento es la diferencia entre\(1\) y la probabilidad de que ocurra el evento. Ver Ejemplo\(\PageIndex{5}\).
- En algunos problemas de probabilidad, necesitamos usar permutaciones y combinaciones para encontrar el número de elementos en eventos y espacios de muestra. Ver Ejemplo\(\PageIndex{6}\).


