11.R: Secuencias, Probabilidad y Teoría del Recuento (Revisión)
- Page ID
- 121341
11.1 Secuencias y sus anotaciones
1) Escribir los primeros cuatro términos de la secuencia definida por la fórmula recursiva\(a_1=2, a_n=a_{n-1}+n\).
- Contestar
-
\(2,4,7,11\)
2) Evaluar\(\dfrac{6!}{(5-3)!3!}\).
3) Escribir los primeros cuatro términos de la secuencia definida por la fórmula explícita\(a_n=10^n+3\).
- Contestar
-
\(13,103,1003,10003\)
4) Escribir los primeros cuatro términos de la secuencia definida por la fórmula explícita\(a_n=\dfrac{n!}{n(n+1)!}\).
11.2 Secuencias Aritméticas
1) ¿La secuencia es\(\dfrac{4}{7},\dfrac{47}{21},\dfrac{82}{21},\dfrac{39}{7},\ldots\) aritmética? Si es así, encuentra la diferencia común.
- Contestar
-
La secuencia es aritmética. La diferencia común es\(d=\dfrac{5}{3}\).
2) ¿La secuencia es\(2,4,8,16,\ldots\) aritmética? Si es así, encuentra la diferencia común.
3) Una secuencia aritmética tiene el primer término\(a_1=18\) y diferencia común\(d=8\). ¿Cuáles son los primeros cinco términos?
- Contestar
-
\(18,10,2,-6,-14\)
4) Una secuencia aritmética tiene términos\(a_3=11.7\) y\(a_8=-14.6\). ¿Cuál es el primer término?
5) Escribir una fórmula recursiva para la secuencia aritmética\(-20,-10,0,10,\ldots\)
- Contestar
-
\(a_1=-20, a_n=a_{n-1}+10\)
6) Escribe una fórmula recursiva para la secuencia aritmética\(0,-\dfrac{1}{2},-1,-\dfrac{3}{2},\ldots\), y luego encuentra el\(31^{st}\) término.
7) Escribir una fórmula explícita para la secuencia aritmética\(\dfrac{7}{8},\dfrac{29}{24},\dfrac{37}{24},\dfrac{15}{8},\ldots\)
- Contestar
-
\(a_n=\dfrac{1}{3}n+\dfrac{13}{24}\)
8) ¿Cuántos términos hay en la secuencia aritmética finita\(12,20,28,\ldots ,172\)?
11.3 Secuencias geométricas
1) Encontrar la relación común para la secuencia geométrica\(2.5, 5, 10, 20,\ldots\)
- Responder
-
\(r=2\)
2) ¿La secuencia es\(4, 16, 28, 40,\ldots\) geométrica? Si es así, encuentra la proporción común. Si no, explica por qué.
3) Una secuencia geométrica tiene términos\(a_7=16,384\) y\(a_9=262,144\). ¿Cuáles son los primeros cinco términos?
- Responder
-
\(4,16,64,256,1024\)
4) Una secuencia geométrica tiene el primer término\(a_1=-3\) y relación común\(r=12\). ¿Cuál es el\(8^{th}\) término?
5) ¿Cuáles son los cinco primeros términos de la secuencia geométrica\(a_1=3, a_n=4\cdot a_{n-1}\)?
- Responder
-
\(3, 12, 48, 192, 768\)
6) Escribir una fórmula recursiva para la secuencia geométrica\(1,\dfrac{1}{3},\dfrac{1}{9},\dfrac{1}{27},\ldots\)
7) Escribir una fórmula explícita para la secuencia geométrica\(-\dfrac{1}{5},-\dfrac{1}{15},-\dfrac{1}{45},-\dfrac{1}{135},\ldots\)
- Responder
-
\(a_n=-\dfrac{1}{5}\cdot \left (\dfrac{1}{3} \right )^{n-1}\)
8) ¿Cuántos términos hay en la secuencia geométrica finita\(-5,-\dfrac{5}{3},-\dfrac{5}{9},\ldots ,-\dfrac{5}{59,049}\)?
11.4 Series y sus anotaciones
1) Utilice la notación de suma para escribir la suma de términos\(\dfrac{1}{2}m+5\) de\(m=0\) a\(m=5\).
- Responder
-
\(\displaystyle \sum_{m=0}^{5}\left (\dfrac{1}{2}m+5 \right )\)
2) Utilice la notación de suma para escribir la suma que resulta de sumar el número\(13\) veinte veces.
3) Utilice la fórmula para la suma de los primeros\(n\) términos de una serie aritmética para encontrar la suma de los primeros once términos de la serie aritmética\(2.5, 4, 5.5,\ldots \)
- Responder
-
\(S_{11}=110\)
4) Una escalera tiene peldaños\(15\) cónicos, cuyas longitudes aumentan por una diferencia común. El primer peldaño mide\(5\) pulgadas de largo y el último peldaño mide\(20\) pulgadas de largo. ¿Cuál es la suma de las longitudes de los peldaños?
5) Utilice la fórmula para la suma de los primeros n términos de una serie geométrica para encontrar\(S_9\) para la serie\(12,6,3,\dfrac{3}{2},\ldots\)
- Responder
-
\(S_9\approx 23.95\)
6) Las cuotas correspondientes a los tres primeros años de afiliación a un club de caza se dan en la siguiente Tabla. Si las cuotas siguen subiendo a la misma tasa, ¿cuánto costará el costo total por los primeros diez años de membresía?
| Año | Cuotas de membresía |
|---|---|
| 1 | $1500 |
| 2 | $1950 |
| 3 | $2535 |
7) Encuentra la suma de la serie geométrica infinita\(\textstyle \sum_{k=1}^{\infty }45\cdot \left ( -\frac{1}{3} \right )^{k-1}\).
- Responder
-
\(S=\dfrac{135}{4}\)
8) Una pelota tiene una relación de rebote de\(35\) la altura del rebote anterior. Escribe una serie que represente la distancia total recorrida por la pelota, asumiendo que inicialmente se cayó desde una altura de\(5\) pies. ¿Cuál es la distancia total? (Pista: la distancia total que recorre la pelota en cada rebote es la suma de las alturas de la subida y la caída.)
9) Alejandro deposita\(\$80\) sus ganancias mensuales en una anualidad que gana intereses\(6.25\%\) anuales, compuesta mensualmente. ¿Cuánto dinero habrá ahorrado después de\(5\) años?
- Responder
-
\(\$5,617.61\)
10) Las gemelas Sarah y Scott abrieron cuentas de jubilación en su\(21^{st}\) cumpleaños. Sarah deposita\(\$4,800.00\) cada año, ganando intereses\(5.5\%\) anuales, compuestos mensualmente. Scott deposita\(\$3,600.00\) cada año, ganando intereses\(8.5\%\) anuales, compuestos mensualmente. ¿Qué gemelo ganará más intereses para cuando tengan\(55\) años? ¿Cuánto más?
11.5 Principios de conteo
1) ¿Cuántas formas hay de elegir un número del conjunto\(\left \{ -10,-6,4,10,12,18,24,32 \right \}\) que sea divisible por cualquiera\(4\) o\(6\)?
- Responder
-
\(6\)
2) En un grupo de\(20\) músicos,\(12\) tocan el piano,\(7\) tocan la trompeta y\(2\) tocan tanto el piano como la trompeta. ¿Cuántos músicos tocan el piano o la trompeta?
3) ¿Cuántas formas hay de construir un código\(4\) -digit si los números pueden repetirse?
- Responder
-
\(10^4=10,000\)
4) Una paleta de pinturas de acuarela tiene\(3\) tonos de verde,\(3\) tonos de azul,\(2\) tonos de rojo,\(2\) tonos de amarillo y\(1\) sombra de negro. ¿Cuántas formas hay de elegir un tono de cada color?
5) Calcular\(P(18,4)\).
- Responder
-
\(P(18,4)=73,440\)
6) En un grupo de\(5\) estudiantes de primer año,\(10\) segundo año,\(3\) juniors y\(2\) seniors, ¿de cuántas maneras se puede elegir a un presidente, vicepresidente y tesorero?
7) Calcular\(C(15,6)\).
- Responder
-
\(C(15,6)=5005\)
8) Una cafetería tiene asados\(7\) guatemaltecos, asados\(4\) cubanos y asados\(10\) costarricenses. ¿De cuántas maneras puede elegir la tienda asados\(2\) guatemaltecos,\(2\) cubanos y\(3\) costarricenses para un evento de degustación de café?
9) ¿Cuántos subconjuntos tiene el conjunto\(\left \{ 1, 3, 5, \ldots , 99 \right \}\)?
- Responder
-
\(2^{50}=1.13\times 10^{15}\)
10) Un spa de día cobra una tarifa diaria básica que incluye el uso de sauna, piscina y duchas. Por un cargo extra, los huéspedes pueden elegir entre los siguientes servicios adicionales: masaje, exfoliación corporal, manicura, pedicura, facial y afeitar recta. ¿Cuántas formas hay de pedir servicios adicionales en el spa de día?
11) ¿De cuántas formas distintas se puede organizar la palabra DEADWOOD?
- Responder
-
\(\dfrac{8!}{3!2!}=3360\)
12) ¿Cuántos reordenamientos distintos de las letras de la palabra DEADWOOD hay si el arreglo debe comenzar y terminar con la letra\(D\)?
11.6 Teorema Binomial
1) Evaluar el coeficiente binomial\(\dbinom{23}{8}\).
- Responder
-
\(490,314\)
2) Utilizar el Teorema Binomial para ampliar\(\left ( 3x+\dfrac{1}{2}y \right )^6\).
3) Utilizar el Teorema Binomial para escribir los tres primeros términos de\((2a+b)^{17}\).
- Responder
-
\(131,072a^{17}+1,114,112a^{16}b+4,456,448a^{15}b^2\)
4) Encontrar el cuarto término de\(\left ( 3a^2-2b \right )^{11}\) sin expandir completamente el binomio.
11.7 Probabilidad
Para los ejercicios 1-7, supongamos que se enrollan dos troqueles.
1) Construir una tabla que muestre el espacio muestral.
- Responder
-
1 2 3 4 5 6 1 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 2 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 3 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 4 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 5 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 6 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6
2) ¿Cuál es la probabilidad de que un rollo incluya un\(2\)?
3) ¿Cuál es la probabilidad de rodar un par?
- Responder
-
\(\dfrac{1}{6}\)
4) ¿Cuál es la probabilidad de que un rollo incluya un\(2\) o resulte en un par?
5) ¿Cuál es la probabilidad de que un rollo no incluya un\(2\) o resultado en un par?
- Responder
-
\(\dfrac{5}{9}\)
6) ¿Cuál es la probabilidad de rodar una\(5\) o una\(6\)?
7) ¿Cuál es la probabilidad de que un rollo incluya ni a\(5\) ni a\(6\)?
- Responder
-
\(\dfrac{4}{9}\)
Para los ejercicios 8-11, utilice los siguientes datos: Una encuesta de la escuela primaria encontró que\(350\) de\(500\) los estudiantes preferían la soda a la leche. Supongamos que\(8\) niños de la escuela están asistiendo a una fiesta de cumpleaños. (Mostrar cálculos y redondear a la décima de un porcentaje más cercana.)
8) ¿Cuál es el porcentaje de probabilidad de que todos los niños que asisten a la fiesta prefieran refrescos?
9) ¿Cuál es el porcentaje de probabilidad de que al menos uno de los niños que asisten a la fiesta prefiera la leche?
- Responder
-
\(1-\dfrac{C(350,8)}{C(500,8)}\approx 94.4\%\)
10) ¿Cuál es el porcentaje de probabilidad de que exactamente\(3\) de los niños que asisten a la fiesta prefieran refrescos?
11) ¿Cuál es el porcentaje de probabilidad de que exactamente\(3\) de los niños que asisten a la fiesta prefieran la leche?
- Responder
-
\(\dfrac{C(150,3)C(350,5)}{C(500,8)}\approx 25.6\%\)
Prueba de práctica
1) Escribir los primeros cuatro términos de la secuencia definida por la fórmula recursiva\(a=-14, a_n=\dfrac{2+a_{n-1}}{2}\)
- Responder
-
\(-14,-6,-2,0\)
2) Escribir los primeros cuatro términos de la secuencia definida por la fórmula explícita\(a_n=\dfrac{n^2-n-1}{n!}\).
3) ¿La secuencia es\(0.3, 1.2, 2.1, 3,\ldots\) aritmética? Si es así, encuentra la diferencia común.
- Responder
-
La secuencia es aritmética. La diferencia común es\(d=0.9\).
4) Una secuencia aritmética tiene el primer término\(a_1=-4\) y diferencia común\(d=-\dfrac{4}{3}\). ¿Cuál es el\(6^{th}\) término?
5) Escribe una fórmula recursiva para la secuencia aritmética\(-2,-\dfrac{7}{2},-5,-\dfrac{13}{2},\ldots\) y luego encuentra el\(22^{nd}\) término.
- Responder
-
\(a_1=-2,a_n=a_{n-1}-\dfrac{3}{2};a_{22}=-\dfrac{67}{2}\)
6) Escribe una fórmula explícita para la secuencia aritmética\(15.6, 15, 14.4, 13.8,\ldots\) y luego encuentra el\(32^{nd}\) término.
7) ¿La secuencia es\(-2,-1,-\dfrac{1}{2},-\dfrac{1}{4},\ldots\) geométrica? Si es así, encuentra la proporción común. Si no, explica por qué.
- Responder
-
La secuencia es geométrica. El cociente común es\(r=\dfrac{1}{2}\).
8) ¿Cuál es el\(11^{th}\) término de la secuencia geométrica\(-1.5,-3,-6,-12,\ldots\)?
9) Escribir una fórmula recursiva para la secuencia geométrica\(1,-\dfrac{1}{2},\dfrac{1}{4},-\dfrac{1}{8},\ldots\)
- Responder
-
\(a_1=1,a_n=-\dfrac{1}{2}\cdot a_{n-1}\)
10) Escribir una fórmula explícita para la secuencia geométrica\(4,-\dfrac{4}{3},\dfrac{4}{9},-\dfrac{4}{27},\ldots\)
11) Utilice la notación de suma para escribir la suma de términos\(3k^2-\dfrac{5}{6}k\) de\(k=-3\) a\(k=15\).
- Responder
-
\(\displaystyle \sum_{k=-3}^{15}\left (3k^2-\dfrac{5}{6}k \right )\)
12) Un estadio de béisbol comunitario tiene\(10\) asientos en la primera fila,\(13\) asientos en la segunda fila,\(16\) asientos en la tercera fila, y así sucesivamente. Hay\(56\) filas en todos. ¿Cuál es la capacidad de asientos del estadio?
13) Usa la fórmula para la suma de los primeros\(n\) términos de una serie geométrica para encontrar\(\displaystyle \sum_{k=1}^{7}-0.2\cdot (-5)^{k-1}\)
- Responder
-
\(S_7=-2604.2\)
14) Encuentra la suma de la serie geométrica infinita\(\displaystyle \sum_{k=1}^{\infty }\dfrac{1}{3}\cdot \left ( -\dfrac{1}{5} \right )^{k-1}\)
15) Rachael deposita\(\$3,600\) en un fondo de retiro cada año. El fondo gana intereses\(7.5\%\) anuales, compuestos mensualmente. Si abrió su cuenta cuando tenía\(20\) años, ¿cuánto tendrá para cuando esté\(55\)? ¿Cuánto de esa cantidad se ganaron los intereses?
- Responder
-
Total en cuenta:\(\$140,355.75\) Intereses devengados:\(\$14,355.75\)
16) En una competencia de bailarines\(50\) profesionales de salón,\(22\) compite en la competencia de fox-trot,\(18\) compite en la competencia de tango, y\(6\) compite tanto en las competencias de fox-trot como de tango. ¿Cuántos bailarines compiten en los concursos de fox-trot o tango?
17) Un comprador de un sedán nuevo puede ordenar el automóvil a medida eligiendo entre\(5\) diferentes colores exteriores,\(3\) diferentes colores interiores, sistemas de\(2\) sonido, diseños de\(3\) motores y transmisión manual o automática. ¿Cuántas opciones tiene el comprador?
- Responder
-
\(5\times 3\times 2\times 3\times 2=180\)
18) Para destinar bonos anuales, un directivo deberá elegir a sus cuatro mejores empleados y clasificarlos primero a cuarto. ¿De cuántas maneras puede crear la lista “Top-Four” de los\(32\) empleados?
19) Un grupo de rock necesita elegir\(3\) canciones para tocar en la batalla anual de las bandas. ¿De cuántas maneras pueden elegir su set si tienen\(15\) canciones para elegir?
- Responder
-
\(C(15,3)=455\)
20) Una tienda de yogurt congelado de autoservicio tiene coberturas de\(8\) dulces y coberturas de\(4\) frutas para elegir. ¿Cuántas formas hay de rematar un yogurt congelado?
21) ¿De cuántas formas distintas se puede disponer la palabra EVANESCENCIA si el anagrama debe terminar con la letra\(E\)?
- Responder
-
\(\dfrac{10!}{2!3!2!}=151,200\)
22) Utilizar el Teorema Binomial para ampliar\(\left (\dfrac{3}{2}x-\dfrac{1}{2}y \right )^5\).
23) Encontrar el séptimo término de\(\left (x^2-\dfrac{1}{2} \right )^{13}\) sin expandir completamente el binomio.
- Responder
-
\(\dfrac{429x^{14}}{16}\)
Para los ejercicios 24-28, usa el spinner en la Figura a continuación.
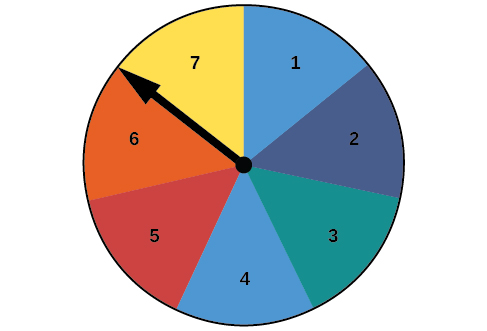
24) Construir un modelo de probabilidad que muestre cada posible resultado y su probabilidad asociada. (Usa la primera letra para los colores.)
25) ¿Cuál es la probabilidad de aterrizar en un número impar?
- Responder
-
\(\dfrac{4}{7}\)
26) ¿Cuál es la probabilidad de aterrizar en azul?
27) ¿Cuál es la probabilidad de aterrizar en azul o un número impar?
- Responder
-
\(\dfrac{5}{7}\)
28) ¿Cuál es la probabilidad de aterrizar en otra cosa que no sea azul o un número impar?
29) Un tazón de caramelo contiene caramelos con sabor\(10\) a\(16\) menta,\(14\) caramelo y fresa. Supongamos que una persona agarra un puñado de\(7\) caramelos. ¿Cuál es el porcentaje de probabilidad de que exactamente\(3\) sean butterscotch? (Mostrar cálculos y redondear a la décima de un porcentaje más cercana.)
- Responder
-
\(\dfrac{C(14,3)C(26,4)}{C(40,7)}\approx 29.2\%\)


