12.1: Encontrar límites - Enfoques numéricos y gráficos

Última actualización
Guardar como PDF

Page ID: 121487

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Intuitivamente, sabemos lo que es un límite. Un auto puede ir tan rápido y no más rápido. Un bote de basura podría contener 33 galones y nada más. Es natural que las cantidades medidas tengan límites. ¿Cuál es, por ejemplo, el límite a la altura de una mujer? La mujer más alta registrada fue Jinlian Zeng de China, quien medía 8 pies 1 pulgadas. ¹ ¿Es este el límite de la estatura a la que pueden crecer las mujeres? Quizás no, pero es probable que haya un límite que podríamos describir en pulgadas si pudiéramos determinar de qué se trataba.

Para decirlo matemáticamente, la función cuya entrada es una mujer y cuya salida es una altura medida en pulgadas tiene un límite. En esta sección, examinaremos enfoques numéricos y gráficos para identificar límites.

Comprensión de la notación límite

Hemos visto cómo una secuencia puede tener un límite, un valor hacia el que se mueve la secuencia de términos a medida que aumenta el número de términos. Por ejemplo, los términos de la secuencia

\[1,\dfrac{1}{2},\dfrac{1}{4},\dfrac{1}{8}... \nonumber \]

se acerca cada vez más a 0. Una secuencia es un tipo de función, pero las funciones que no son secuencias también pueden tener límites. Podemos describir el comportamiento de la función a medida que los valores de entrada se acercan a un valor específico. Si el límite de una función$f(x)=L$, entonces a medida que la entrada$x$ se acerca cada vez más$a$, la coordenada y de salida se acerca cada vez más$L$. Decimos que la salida “se acerca”$L$.

La figura$\PageIndex{1}$ proporciona una representación visual del concepto matemático de límite. A medida que se$x$ acerca el valor de entrada$a$, el valor de salida$f(x)$ se acerca a

Figura$\PageIndex{1}$: La salida (coordenada y) se aproxima a$L$ medida que se acerca la entrada (coordenada x)$a$.

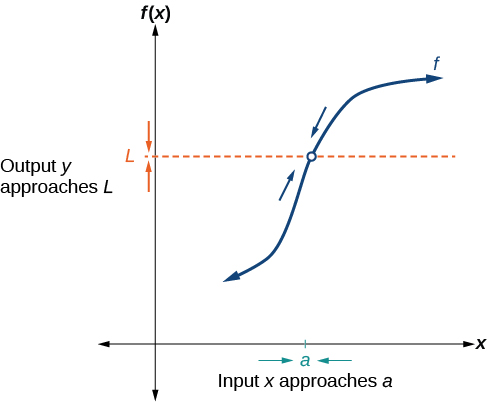
Escribimos la ecuación de un límite como

\[\lim_{x \to a} f(x)=L. \nonumber \]

Esta notación indica que a medida que$x$ se aproxima$a$ tanto desde la$x=a$ izquierda como desde la derecha$x=a,$ del valor de salida se aproxima$L.$

Considera la función

\[f(x)=\dfrac{x^2−6x−7}{x−7}. \label{eq1}\]

Podemos factorial la función en la Ecuación\ ref {eq1} como se muestra.

\[\begin{array}{ll} f(x)=\dfrac{\cancel{(x−7)}(x+1)}{\cancel{x−7}} & \text{Cancel like factors in numerator and denominator.} \\ f(x)=x+1,x≠7 & \text{Simplify.} \end{array} \nonumber \]

Observe que$x$ no puede ser 7, o estaríamos dividiendo por 0, así que 7 no está en el dominio de la función en la Ecuación\ ref {eq1}. Para evitar cambiar la función cuando simplificamos, establecemos la misma condición,$x≠7$, para la función simplificada. Podemos representar la función gráficamente como se muestra en la Figura$\PageIndex{2}$.

Figura$\PageIndex{2}$: Debido a que 7 no está permitido como entrada, no hay ningún punto en$x=7$.

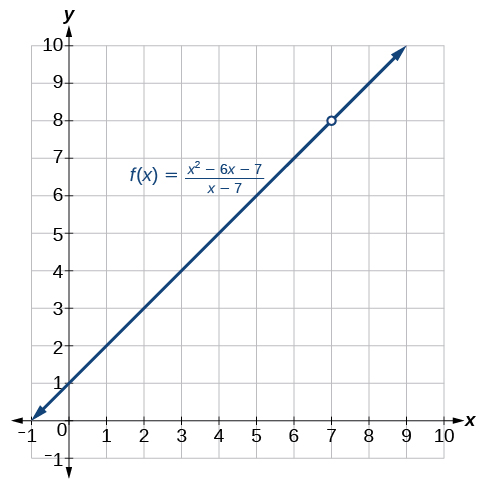
Lo que sucede en$x=7$ es completamente diferente de lo que ocurre en puntos cercanos a uno y otro$x=7$ lado. La notación

\[\lim_{x \to 7} f(x)=8 \nonumber \]

indica que a medida que la entrada$x$ se acerca a 7 ya sea desde la izquierda o desde la derecha, la salida se acerca a 8. La salida puede llegar tan cerca de 8 como queramos si la entrada está suficientemente cerca de 7.

¿Qué pasa en$x=7$? Cuando$x=7$, no hay salida correspondiente. Escribimos esto como

\[f(7) \text{does not exist.} \nonumber \]

Esta notación indica que 7 no está en el dominio de la función. Ya habíamos indicado esto cuando escribimos la función como

\[f(x)=x+1, x≠7. \nonumber \]

Observe que el límite de una función puede existir aunque no$f(x)$ esté definido en$x=a.$ Gran parte de nuestro trabajo posterior será determinar límites de funciones a medida que$x$ se acerque$a$, aunque la salida en$x=a$ no exista.

EL LÍMITE DE UNA FUNCIÓN

Una cantidad$L$ es el límite de una función$f(x)$ como$x$ se acerca$a$ si, como los valores de entrada de$x$ aproximación$a$ (pero no iguales$a$), los valores de salida correspondientes de$f(x)$ acercarse a$L$. Tenga en cuenta que el valor del límite no se ve afectado por el valor de salida de$f(x)$ at$a$. Ambos$a$ y$L$ deben ser números reales. Lo escribimos como

\[ \lim_{x \to a} f(x)=L \nonumber \]

Ejemplo$\PageIndex{1}$: Understanding the Limit of a Function

Para el siguiente límite, defina$a,f(x),$ y$L.$

\[ \lim_{x \to 2} (3x+5)=11 \nonumber \]

Solución

Primero, reconocemos la notación de un límite. Si el límite existe, a medida que$x$ se aproxima$a$, escribimos

\[ \lim_{x \to a} f(x)=L. \nonumber \]

Se nos da

\[ \lim_{x \to 2} (3x+5)=11. \nonumber \]

Esto significa que$a=2,f(x)=3x+5,$ y$L=11.$

Análisis

Recordemos que$y=3x+5$ es una línea sin roturas. A medida que los valores de entrada se acercan a 2, los valores de salida se acercarán a 11. Esto puede formularse con la ecuación$ \lim_{x \to 2}(3x+5)=11,$ lo que significa que a medida que se$x$ acerca a 2 (pero no es exactamente 2), la salida de la función$f(x)=3x+5$ se acerca lo más que queremos$3(2)+5,$ o$11$, que es el límite$L$, ya que tomamos valores de$x$ suficientemente cerca de 2 pero no en $x=2$.

Ejercicio$\PageIndex{1}$

Para el siguiente límite, defina$a,f(x)$, y$L$.

\[ \lim_{x \to 5} (2x^2 −4)=46 \nonumber \]

Solución

$a=5, f(x)=2x^2−4,$y$L=46.$

Comprensión de los límites de la mano izquierda y de la derecha

Podemos acercarnos a la entrada de una función desde cualquier lado de un valor, desde la izquierda o la derecha. La figura$\PageIndex{3}$ muestra los valores de

\[f(x)=x+1,x≠7 \nonumber \]

como se describió anteriormente y se representa en la Figura$\PageIndex{3}$.

La figura$\PageIndex{3}$ son$6.9, 6.99,$ y$6.999$. Las salidas correspondientes son$7.9,7.99,$ y$7.999.$ Estos valores se están acercando a 8. El límite de valores de$f(x)$ como se$x$ aproxima desde la izquierda se conoce como el límite de la izquierda. Para esta función, 8 es el límite izquierdo de la función a$f(x)=x+1,x≠7$ medida que se$x$ acerca a 7.

Los valores descritos como “desde la derecha” son mayores que el valor de entrada 7 y, por lo tanto, aparecerían a la derecha del valor en una recta numérica. Los valores de entrada que se acercan a 7 desde la derecha en la Figura$\PageIndex{3}$ son$7.1, 7.01, $ y$7.001.$ Las salidas correspondientes son$8.1, 8.01,$ y$8.001.$ Estos valores se están acercando a 8. El límite de valores de$f(x)$ como se$x$ aproxima desde la derecha se conoce como el límite de la derecha. Para esta función, 8 es también el límite de la derecha de la función a$f(x)=x+1,x≠7$ medida que se$x$ acerca a 7.

La figura$\PageIndex{3}$ muestra que podemos obtener la salida de la función dentro de una distancia de 0.1 de 8 mediante el uso de una entrada dentro de una distancia de 0.1 de 7. En otras palabras, necesitamos una entrada$x$ dentro del intervalo$6.9<x<7.1$ para producir un valor de salida$f(x)$ dentro del intervalo$7.9<f(x)<8.1.$

También vemos que podemos obtener valores de salida de$f(x)$ sucesivamente más cercanos a 8 seleccionando valores de entrada más cercanos a 7. De hecho, podemos obtener valores de salida dentro de cualquier intervalo especificado si elegimos valores de entrada apropiados.

La figura$\PageIndex{4}$ proporciona una representación visual de los límites izquierdo y derecho de la función. A partir de la gráfica de$f(x)$, observamos que la salida puede llegar infinitesimalmente cerca a$L=8$ medida que$x $ se acerca a 7 desde la izquierda y como$x$ se acerca a 7 desde la derecha.

Para indicar el límite de la izquierda, escribimos

\[ \lim_{x \to 7^−} f(x)=8. \nonumber \]

Para indicar el límite de la derecha, escribimos

\[\lim_{x \to 7^+} f(x)=8. \nonumber \]

Figura$\PageIndex{4}$: Los límites izquierdo y derecho son los mismos para esta función.

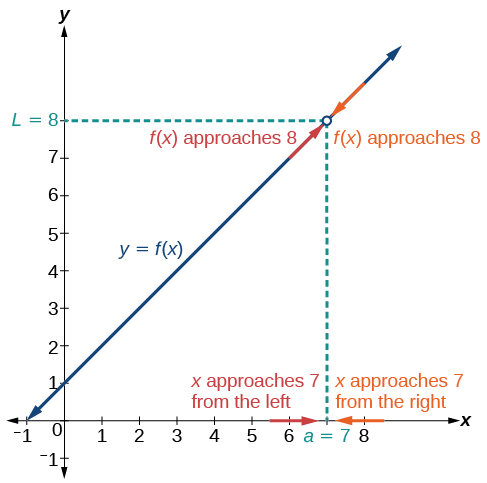
LÍMITES IZQUIERDA Y DERECHA

El límite izquierdo de una función a$f(x)$ medida que$x$ se$a$ aproxima desde la izquierda es igual a$L$, denotado por\[\lim_{x \to a^−}f(x)=L. \nonumber \]

Los valores de$f(x)$ pueden llegar lo más cerca del límite$L$ como queramos tomando valores de$x$ suficientemente cerca de$a$ tal manera que$x<a$ y$x≠a.$

El límite derecho de una función a$f(x),$ medida que$x$ se$a$ aproxima desde la derecha, es igual a$L,$ denotado por\[ \lim_{x \to a^+} f(x)=L. \nonumber \]

Los valores de$f(x)$ pueden llegar lo más cerca del límite$L$ como queramos tomando valores de$x$ suficientemente cerca$a$ pero mayores que$a$. Ambos$a$ y$L$ son números reales.

Comprender los límites de dos caras

En el ejemplo anterior, el límite de la izquierda y el límite de la derecha como$x$ aproximaciones$a$ son iguales. Si los límites izquierdo y derecho son iguales, decimos que la función$f(x)$ tiene un límite de dos lados a medida que$x $ se acerca$a.$ Más comúnmente, simplemente nos referimos a un límite de dos lados como un límite. Si el límite de la izquierda no es igual al límite de la derecha, o si uno de ellos no existe, decimos que el límite no existe.

El límite de una función$f(x)$, a medida que se$x$$a$ aproxima$L$, es decir,\[ \lim_{x \to a} f(x)=L \nonumber \] si y solo si\[\lim_{x \to a^−} f(x)= \lim_{x \to a^+} f(x). \nonumber \]

En otras palabras, el límite de la izquierda de una función$f(x)$ como$x$ enfoques$a$ es igual al límite de la derecha de la misma función que$x$ los enfoques$a.$ Si existe tal límite, nos referimos al límite como un límite de dos lados. De lo contrario decimos que el límite no existe.

Encontrar un límite usando una gráfica

Para determinar visualmente si existe un límite como$x$ aproximaciones$a$, observamos la gráfica de la función cuando$x$ está muy cerca de$x=a.$ En la Figura$\PageIndex{5}$ observamos el comportamiento de la gráfica en ambos lados de a.

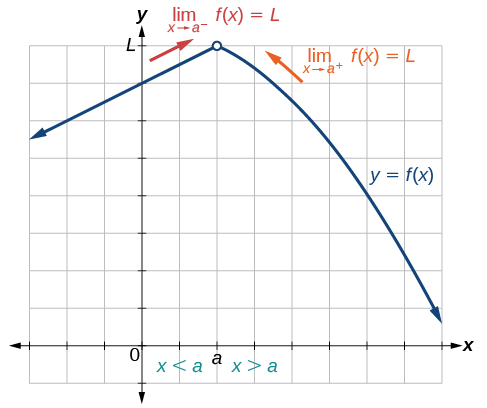
Para determinar si existe un límite de la izquierda, observamos la rama de la gráfica a la izquierda de$x=a$, pero cerca$x=a$. Aquí es donde$x<a.$ Vemos que las salidas se están acercando a algún número real$L$ por lo que hay un límite de la izquierda.

Para determinar si existe un límite de la derecha, observe la rama de la gráfica a la derecha de$x=a,$ pero cerca$x=a$. Aquí es donde$x>a$. Vemos que las salidas se están acercando a algún número real$L$, por lo que hay un límite de la derecha.

Si el límite de la izquierda y el límite de la derecha son los mismos, como son en la Figura$\PageIndex{5}$, entonces sabemos que la función tiene un límite de dos lados. Normalmente, cuando nos referimos a un “límite”, nos referimos a un límite de dos lados, a menos que lo llamemos límite unilateral.

Finalmente, podemos buscar un valor de salida para la función$f(x)$ cuando el valor de entrada$x$ es igual a$a$. El par de coordenadas del punto sería$(a,f(a)).$ Si tal punto existe, entonces$f(a)$ tiene un valor. Si el punto no existe, como en la Figura$\PageIndex{5}$, entonces decimos que$f(a)$ no existe.

CÓMO: Dada una función$f(x)$, use a graph to find the limits and a function value as $x$ approaches $a.$

Examine la gráfica para determinar si existe un límite a la izquierda.
Examine la gráfica para determinar si existe un límite de la derecha.
Si los dos límites unilaterales existen y son iguales, entonces hay un límite de dos lados, lo que normalmente llamamos un “límite”.
Si hay un punto en$x=a,$ entonces$f(a)$ es el valor de la función correspondiente.

Ejemplo$\PageIndex{2}$: Finding a Limit Using a Graph

Determine los siguientes límites y el valor de función para la función que$f$ se muestra en la Figura$\PageIndex{6}$.

$ \lim_{x \to 2^−} f(x)$
$ \lim_{x \to 2^+} f(x)$
$ \lim_{x \to 2} f(x)$
$f(2)$

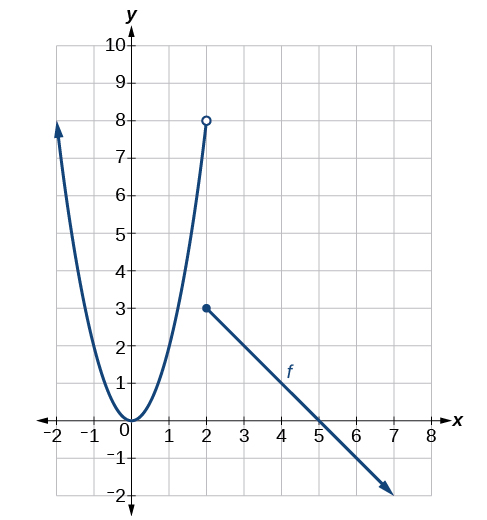
Determine los siguientes límites y el valor de función para la función f f que se muestra en la Figura.

$ \lim_{x \to 2^−} f(x)$
$ \lim_{x \to 2^+} f(x)$
$ \lim_{x \to 2} f(x)$
$f(2)$

Mirando la Figura:
1. $\lim_{x \to 2^−} f(x)=8; $cuando$x<2$, pero infinitesimalmente cerca de 2, los valores de salida se acercan a$y=8$.
2. $ \lim_{x \to 2^+} f(x)=3;$cuando$x>2$, pero infinitesimalmente cerca de 2, los valores de salida se acercan$y=3$.
3. $ \lim_{x \to 2} f(x)$no existe porque$ \lim_{x \to 2 ^−} f(x)≠ \lim_{x \to 2^+} f(x);$ los límites izquierdo y derecho no son iguales.
4. $f(2)=3$porque la gráfica de la función$f$ pasa por el punto$(2,f(2))$ o$(2,3).$
Mirando la Figura:
1. $\lim_{x \to 2^−} f(x)=8; $cuando$x<2$ pero infinitesimalmente cerca de 2, los valores de salida se acercan$y=8.$
2. $\lim_{x \to 2^+} f(x)=8; $cuando$x>2$ pero infinitesimalmente cerca de 2, los valores de salida se acercan$y=8$.
3. $\lim_{x \to 2} f(x)=8; $porque$ \lim_{x \to 2^−} f(x)= \lim_{x \to 2^+} f(x)=8;$ los límites izquierdo y derecho son iguales.
4. $f(2)=4$porque la gráfica de la función$f$ pasa por el punto$(2,f(2))$ o$(2,4)$.

Ejercicio$\PageIndex{2}$:

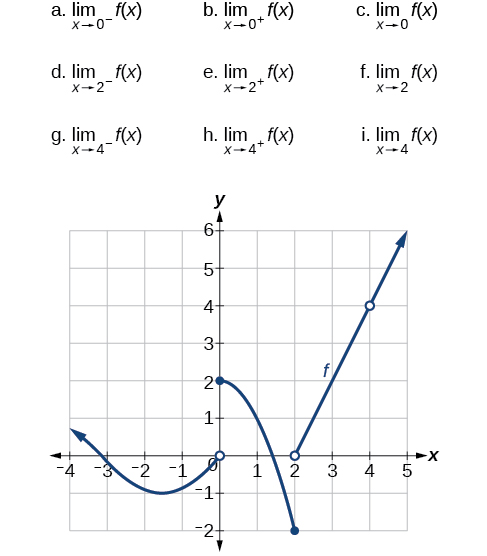
Utilizando la gráfica de la función y=f (x) y=f (x) mostrada en la Figura, estime los siguientes límites.

$Gráfica de una función por partes que tiene tres segmentos: 1) infinito negativo a 0, 2) 0 a 2, y 3) 2 a inifnidad positiva, que tiene una discontinuidad en (4, 4)$

Solución

a. 0; b. 2; c. no existe; d.−2; −2; e. 0; f. no existe; g. 4; h. 4; i. 4

Encontrar un límite usando una tabla

Crear una tabla es una forma de determinar límites usando información numérica. Creamos una tabla de valores en la que los valores de entrada de$x$ aproximación$a$ desde ambos lados. Entonces determinamos si los valores de salida se acercan cada vez más a algún valor real, el límite$L$.

Consideremos un ejemplo usando la siguiente función:

\[ \lim_{x \to 5} \left( \dfrac{x^3−125}{x−5} \right) \nonumber \]

Para crear la tabla, evaluamos la función en valores cercanos a$x=5$. Usamos algunos valores de entrada menores a 5 y algunos valores mayores a 5 como en la Figura. Los valores de la tabla muestran que cuando$x>5$ pero acercándose a 5, la salida correspondiente se acerca a 75. Cuando$x>5$ pero acercándose a 5, la salida correspondiente también se acerca a 75.

$CNX_Precalc_Figure_12_01_008n.jpg$

Porque

\[\lim_{x \to 5^−} f(x)=75= \lim_{x \to 5^+} f(x), \nonumber \]

entonces

\[ \lim_{x \to 5} f(x)=75. \nonumber \]

Recuerda que$f(5)$ no existe.

Cómo: Dada una función$f$,use a table to find the limit as $x$ approaches $a$ and the value of $f(a)$, if it exists.

Elija varios valores de entrada que se acerquen a a tanto desde la izquierda como desde la derecha. Grabe en una mesa.
Evaluar la función en cada valor de entrada. Grabe en la mesa.
Determine si los valores de la tabla indican un límite de la izquierda y un límite de la derecha.
Si los límites izquierdo y derecho existen y son iguales, hay un límite de dos lados.
Reemplazar$x$ con$a$ para encontrar el valor de$f(a)$.

Ejemplo$\PageIndex{3}$: Finding a Limit Using a Table

Estimar numéricamente el límite de la siguiente expresión estableciendo una tabla de valores a ambos lados del límite.

\[\lim_{x \to 0} \left( \dfrac{5 \sin(x)}{3x} \right) \nonumber \]

Solución

Podemos estimar el valor de un límite, si existe, evaluando la función a valores cercanos$x=0$. No podemos encontrar un valor de función para$x=0$ directamente porque el resultado tendría un denominador igual a 0, y por lo tanto estaría indefinido.

\[ f(x)= \dfrac{5 \sin (x)}{3x} \nonumber \]

Creamos Figura eligiendo varios valores de entrada cercanos a$x=0,$ con la mitad de ellos menos que$x=0$ y la mitad de ellos mayores que$x=0.$ Tenga en cuenta que necesitamos estar seguros de que estamos usando el modo radián. Evaluamos la función en cada valor de entrada para completar la tabla.

Los valores de la tabla indican que cuando$x<0$ pero acercándose a 0, la salida correspondiente se acerca$\frac{5}{3}.$

Cuando$x>0$ pero acercándose a 0, la salida correspondiente también se acerca$\frac{5}{3}.$

$CNX_Precalc_Figure_12_01_009.jpg$

Porque

\[ \lim_{x \to 0^−} f(x)=\dfrac{5}{3} = \lim_{x \to 0^+} f(x), \nonumber \]

entonces

\[\lim_{x \to 0} f(x)=\dfrac{5}{3}. \nonumber \]

P & A: ¿Es posible verificar nuestra respuesta usando una utilidad gráfica?

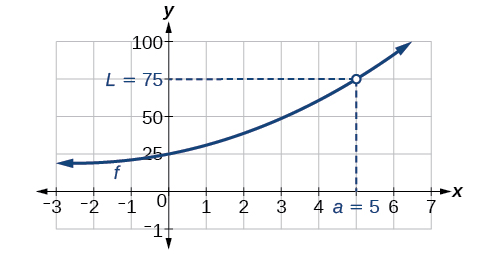
Sí. Anteriormente se utilizó una tabla para encontrar un límite de 75 para la función a $f(x)=\frac{x^3−125}{x−5}$medida que se$x$ acerca a 5. Para verificar, graficamos la función en una ventana de visualización como se muestra en la Figura. Una comprobación gráfica muestra que ambas ramas de la gráfica de la función se acercan a la salida 75 a medida que se$x$ acerca a 5. Además, podemos usar la función 'trace' de una calculadora gráfica. Al appraoching$x=5$ podemos observar numéricamente las salidas correspondientes acercándose a 75.

$CNX_Precalc_Figure_12_01_010F.jpg$

Ejercicio$\PageIndex{3}$:

Estimar numéricamente el límite de la siguiente función haciendo una tabla:

\[ \lim_{x \to 0} \left( \dfrac{20 \sin (x)}{4x} \right) \nonumber \]

Solución

\[ \lim_{x \to 0} \left( \dfrac{20 \sin (x)}{4x} \right) = 5 \nonumber \]

$CNX_Precalc_Figure_12_01_014.jpg$

Q & A

¿Un método para determinar un límite es mejor que el otro?

No. Ambos métodos tienen ventajas. La gráfica permite una inspección rápida. Las tablas se pueden usar cuando las utilidades gráficas no están disponibles, y se pueden calcular con una precisión más alta que la que se podría ver con una inspección visual sin ayuda de una gráfica.

Ejemplo$\PageIndex{4}$: Using a Graphing Utility to Determine a Limit

Con el uso de una utilidad gráfica, si es posible, determinar los límites izquierdo y derecho de la siguiente función como se$x$ acerca a 0. Si la función tiene un límite a medida que se$x$ acerca a 0, indíquelo. Si no, discuta por qué no hay límite.

\[f(x)=3 \sin (\dfrac{π}{x}) \nonumber \]

Solución

Podemos usar una utilidad gráfica para investigar el comportamiento de la gráfica cercana a$x=0$. Centrándonos alrededor$x=0,$ elegimos dos ventanas de visualización de tal manera que la segunda se$x=0$ acerque más que la primera. El resultado se asemejaría a Figura para$[−2,2]$ por$[−3,3]$.

Figure_12_01_012">Figura para$[−0.1,0.1]$ por$[−3,3]$.

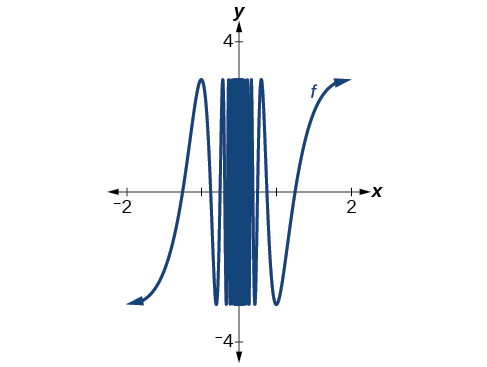
Aún más cerca de cero, somos aún menos capaces de distinguir cualquier límite.

Cuanto más nos acercamos a 0, mayores son las oscilaciones en los valores de salida. Ese no es el comportamiento de una función con un límite de la izquierda o de la derecha. Y si no hay límite a la izquierda o a la derecha, ciertamente no hay límite para la función$f(x)$ ya que se$x$ acerca a 0.

Escribimos

\[ \lim_{x \to 0^−} \left( 3 \sin \left( \dfrac{π}{x} \right) \right) \;\;\; \text{does not exist.} \nonumber \]

\[ \lim_{x \to 0^+} \left( 3 \sin \left( \dfrac{π}{x} \right) \right) \;\;\; \text{does not exist.} \nonumber \]

\[ \lim_{x \to 0} \left( 3 \sin \left( \dfrac{π}{x} \right) \right) \;\;\; \text{does not exist.} \nonumber \]

Ejercicio$\PageIndex{4}$:

Estimar numéricamente el siguiente límite:$ \lim \limits_{x \to 0} (\sin (\frac{2}{x}))$.

Solución

no existe

Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con límites de búsqueda.

Conceptos clave

Una función tiene un límite si los valores de salida se acercan a algún valor a$L$ medida que los valores de entrada se acercan a alguna cantidad a. a. Ver Ejemplo.
Se utiliza una notación taquigráfica para describir el límite de una función según la forma$ \lim \limits_{x \to a} f(x)=L,$ que indica que a medida que$x$ se aproxima$a$, tanto desde la izquierda como desde la derecha$x=a,$ del valor de salida se acerca a$x=a$$L.$
Una función tiene un límite de la izquierda si$f(x)$ se acerca$L$ como se$x$ acerca a un a donde La función$x<a.$ A tiene un límite de la derecha si$f(x)$ se acerca$L$ como$x$ se acerca$a$ donde$x>a$.
Existe un límite de dos lados si el límite de la izquierda y el límite de la derecha de una función son los mismos. Se dice que una función tiene un límite si tiene un límite de dos lados.
Una gráfica proporciona un método visual para determinar el límite de una función.
Si la función tiene un límite a medida que$x$ se acerca$a$, las ramas de la gráfica se acercarán a la misma$y-$ coordenada cerca$x=a$ de la izquierda y la derecha. Ver Ejemplo.
Se puede usar una tabla para determinar si una función tiene un límite. La tabla debe mostrar valores de entrada que se acerquen$a$ desde ambas direcciones para que los valores de salida resultantes puedan ser evaluados. Si los valores de salida se acercan a algún número, la función tiene un límite. Ver Ejemplo.
Una utilidad gráfica también se puede utilizar para encontrar un límite. Ver Ejemplo.

Notas al pie

1 https://en.Wikipedia.org/wiki/Human_height y http://en.Wikipedia.org/wiki/List_of_tallest_people

Glosario

Límite izquierdo: el límite de valores de$f(x) \nonumber $ como$x$ se aproxima desde$a$ la izquierda, denotado\[\lim \limits_{x \to a^−} f(x)=L. \nonumber \] Los valores de$f(x) \nonumber $ pueden llegar lo más cerca del límite$L$ como queramos tomando valores de$x$ suficientemente cercanos a un tal que$x<a \nonumber $ y $x≠a. \nonumber $. Ambos$a$ y$L$ son números reales.

límite: cuando existe, el valor,$L$, que la salida de una función se$f(x)$ acerca a medida que la entrada$x$ se acerca cada vez más a$a$ pero no es igual$a$. El valor de la salida,$f(x), \nonumber $ puede llegar lo más cerca que elegimos para hacerla mediante el uso de valores de entrada de$x$ suficientemente cerca a$x=a$, pero no necesariamente a$x=a$.$L$ Ambos$a$ y$L$ son números reales, y$L$ se denota\[\lim \limits_{x \to a}f(x)=L. \nonumber \]

Límite derecho: el límite de valores de$f(x)$ como$x$ se$a$ aproxima desde la derecha, denotado\[\lim \limits_{x \to a^+}f(x)=L. \nonumber \] Los valores de$f(x)$ pueden llegar lo más cerca del límite$L$ como queramos tomando valores de$x$ suficientemente cerca de$a$ donde $x>a,$ y$x≠a.$ Ambos$a$ y$L$ son números reales.

límite de dos caras: el límite de una función a\[f(x), \nonumber \] medida que se$x$ acerca$a$, es igual a$L$, es decir,\[\lim \limits_{x \to a} f(x)=L \nonumber \] si y sólo si\[\lim \limits_{x \to a^−} f(x)= \lim \limits_{x \to a^+}f(x). \nonumber \]