12.2: Encontrar límites - Propiedades de límites

Última actualización
Guardar como PDF

Page ID: 121504

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Considerar la función racional

\[f(x)=\dfrac{x^2−6x−7}{x−7} \nonumber \]

La función se puede factorizar de la siguiente manera:

\[f(x)=\dfrac{\cancel{(x−7)}(x+1)}{\cancel{x−7}} \nonumber \]

lo que nos da

\[f(x)=x+1,x≠7. \nonumber \]

¿Significa esto que la función$f(x)$ es la misma que la función?$g(x)=x+1?$

La respuesta es no. La función$f(x)$ no tiene$x=7$ en su dominio, pero$g(x)$ sí. Gráficamente, observamos que hay un agujero en la gráfica de$f(x)$ at$x=7$, como se muestra en la Figura y no hay tal agujero en la gráfica de$g(x)$, como se muestra en la Figura.

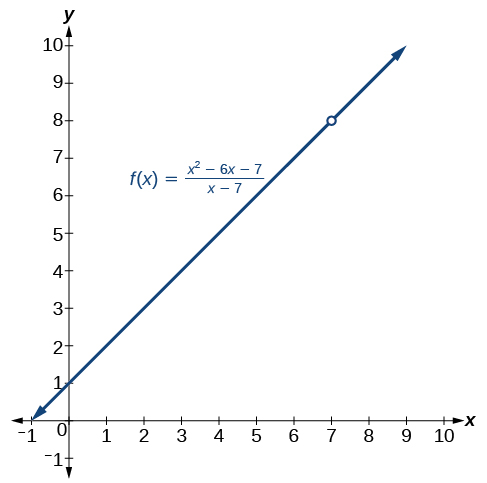
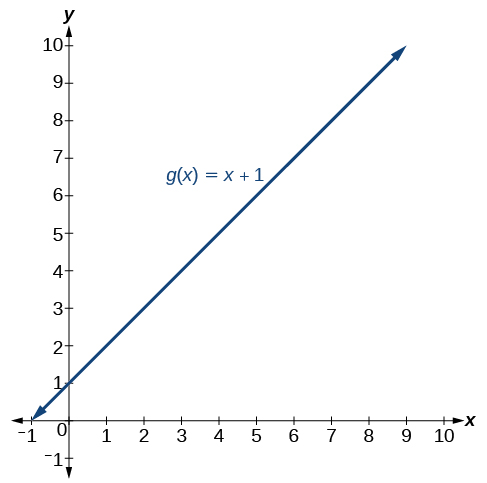
$CNX_Precalc_Figure_12_02_001.jpg$ $CNX_Precalc_Figure_12_02_002.jpg$

(izquierda) La gráfica de la función$f$ contiene una interrupción en$x=7$ y, por lo tanto, no es continua en$x=7$. (Derecha) La gráfica de la función$g$ es continua.

Entonces, ¿estas dos funciones diferentes también tienen límites diferentes a medida que se$x$ aproxima 7? No necesariamente. Recuerde, al determinar un límite de una función a medida que$x$ se aproxima$a$, lo que importa es si la salida se acerca a un número real a medida que nos acercamos$x=a$. La existencia de un límite no depende de lo que suceda cuando$x$ es igual$a$.

Vuelva a mirar Figura y Figura. Observe que en ambas gráficas, a medida que$x$ se acerca a 7, los valores de salida se acercan a Esto significa

\[ \lim \limits_{x \to 7} f(x)= \lim \limits_{x \to 7} g(x). \nonumber \]

Recuerda que a la hora de determinar un límite, la preocupación es lo que ocurre cerca$x=a$, no en$x=a$. En esta sección, utilizaremos una variedad de métodos, como reescribir funciones por factorización, para evaluar el límite. Estos métodos nos darán una verificación formal de lo que antes logramos por intuición.

Encontrar el límite de una suma, una diferencia y un producto

Graficar una función o explorar una tabla de valores para determinar un límite puede ser engorroso y llevar mucho tiempo. Cuando es posible, es más eficiente utilizar las propiedades de los límites, que es una colección de teoremas para encontrar límites.

Conocer las propiedades de los límites nos permite computar los límites directamente. Podemos sumar, restar, multiplicar y dividir los límites de funciones como si estuviéramos realizando las operaciones sobre las propias funciones para encontrar el límite del resultado. De igual manera, podemos encontrar el límite de una función elevada a un poder elevando el límite a ese poder. También podemos encontrar el límite de la raíz de una función tomando la raíz del límite. Usando estas operaciones en límites, podemos encontrar los límites de funciones más complejas al encontrar los límites de sus funciones componentes más simples.

propiedades de límites

Dejar$a, k, A,$ y$B$ representar números reales,$f$ y$g$ ser funciones, tal que$\lim \limits_{x \to a} f(x)=A$ y$ \lim \limits_{x \to a}g(x)=B.$ Para los límites que existen y son finitos, las propiedades de los límites se resumen en Tabla

Constante, k	$\lim \limits_{x \to a} k=k $
Tiempos constantes de una función	$\lim \limits_{x \to a} [k⋅f(x)]=k \lim \limits_{x \to a} f(x)=kA$
Suma de funciones	$\lim \limits_{x \to a} [f(x)+g(x)]= \lim \limits_{x \to a}f(x)+ \lim \limits_{x to a} g(x)=A+B$
Diferencia de funciones	$\lim \limits_{x \to a} [f(x)−g(x)]= \lim \limits_{x \to a} f(x)− \lim \limits_{x \to a} g(x)=A−B$
Producto de funciones	$ \lim \limits _{x \to a}[f(x)⋅g(x)]= \lim \limits _{x \to a}f(x)⋅ \lim \limits_{x \to a} g(x)=A⋅B$
Cociente de funciones	$\lim \limits _{x \to a} \frac{f(x)}{g(x)}= \frac{\lim \limits _{x \to a}f(x) }{\lim \limits _{x \to a}g(x)}=\frac{A}{B},B≠0$
Función elevada a un exponente	$\lim \limits _{x \to a}[f(x)]^n=[\lim \limits _{x \to ∞}f(x)]^n=A^n$, donde$n$ es un entero positivo
n ésima raíz de una función, donde n es un entero positivo	$\lim \limits _{x \to a}f(x) \sqrt[n]{f(x)} = \sqrt[n]{ \lim \limits _{x \to a}[ f(x) ]}=\sqrt[n]{A}$
Función polinomial	$ \lim \limits _{x \to a} p(x)=p(a)$

Ejemplo$\PageIndex{1}$: Evaluating the Limit of a Function Algebraically

Evaluar\[\lim \limits _{x \to 3}(2x+5). \nonumber \]

Solución

\[\begin{align} \lim \limits _{x \to 3}(2x+5) &= \lim \limits _{x \to 3} (2x)+\lim \limits _{x \to 3}(5) && \text{Sum of functions property} \\ &=2 \lim \limits_{ x \to 3}(x)+\lim \limits _{x \to 3}(5) && \text{Constant times a function property} \\ &=2(3)+5 && \text{Evaluate} \\ &=11 \end{align} \nonumber \]

Ejercicio$\PageIndex{1}$:

Evalúe el siguiente límite:\[\lim \limits_{x \to −12}(−2x+2). \nonumber \]

Solución

Encontrar el límite de un polinomio

No todas las funciones o sus límites implican una simple suma, resta o multiplicación. Algunos pueden incluir polinomios. Recordemos que un polinomio es una expresión que consiste en la suma de dos o más términos, cada uno de los cuales consiste en una constante y una variable elevada a una potencia integral no negativa. Para encontrar el límite de una función polinómica, podemos encontrar los límites de los términos individuales de la función, y luego sumarlos juntos. Además, el límite de una función polinómica como$x$ enfoques$a$ equivale a simplemente evaluar la función para$a$.

cómo: Dada una función que contiene un polinomio, encontrar su límite

Utilice las propiedades de los límites para dividir el polinomio en términos individuales.
Encuentra los límites de los términos individuales.
Sumar los límites juntos.
Alternativamente, evaluar la función para$a$.

Ejemplo$\PageIndex{1}$: Evaluating the Limit of a Function Algebraically

Evaluar\[ \lim \limits_{x \to 3}(5x ^2). \nonumber \]

Solución

\[\begin{align} \lim \limits_{x \to 3}(5x^2) &= 5 \lim \limits_{x \to 3}(x^2) && \text{Constant times a function property} \\ &=5(3^2) && \text{Function raised to an exponent property} \\&=45 \end{align} \nonumber \]

Ejercicio$\PageIndex{1}$:

Evaluar\[ \lim \limits_{x \to 4} (x^3−5). \nonumber \]

Solución

Ejemplo$\PageIndex{2}$: Evaluating the Limit of a Polynomial Algebraically

Evaluar\[ \lim \limits_{x \to 5} (2x^3−3x+1). \nonumber \]

Solución

\[\begin{align} \lim \limits_{x \to 5}(2x^3−3x+1) &= \lim \limits_{x \to 5}(2x3)−\lim \limits_{x \to 5}(3x)+\lim \limits_{x \to 5} (1) && \text{Sum of functions}\\ &= 2 \lim \limits_{x \to 5}(x^3)−3 \lim \limits_{x \to 5}(x)+\lim \limits_{x \to 5}(1) && \text{Constant times a function} \\ &=2(5^3)−3(5)+1 && \text{Function raised to an exponent} \\ &=236 &&\text{Evaluate} \end{align} \nonumber \]

Ejercicio$\PageIndex{2}$:

Evalúe el siguiente límite:\[\lim \limits_{x \to −1}(x^4−4x^3+5). \nonumber \]

Solución

Encontrar el límite de un poder o una raíz

Cuando un límite incluye un poder o una raíz, necesitamos otra propiedad que nos ayude a evaluarlo. El cuadrado del límite de una función es igual al límite del cuadrado de la función; lo mismo va para las potencias superiores. Asimismo, la raíz cuadrada del límite de una función es igual al límite de la raíz cuadrada de la función; lo mismo se aplica a las raíces superiores.

Ejemplo$\PageIndex{3}$: Evaluating a Limit of a Power

Evaluar\[ \lim \limits_{x \to 2}(3x+1)^5. \nonumber \]

Solución

Tomaremos el límite de la función a medida que$x$ se acerca a 2 y elevaremos el resultado a la ^5ª potencia.

\[\begin{align} \lim \limits_{x \to 2} (3x+1)^5 &= (\lim \limits_{x \to 2}(3x+1))^5 \\ &=(3(2)+1)^5 \\ &=7^5 \\ &=16,807 \end{align} \nonumber \]

Ejercicio$\PageIndex{3}$:

Evalúe el siguiente límite:$ \lim \limits_{x \to −4}(10x+36)^3.$

Solución

−64

P & A: Si no podemos aplicar directamente las propiedades de un límite, por ejemplo en$\lim \limits_{x \to 2}(\frac{x^2+6x+8}{x−2})$, can we still determine the limit of the function as $x$ approaches $a$?

Sí. Algunas funciones pueden ser reordenadas algebraicamente para que se pueda evaluar el límite de una forma equivalente simplificada de la función.

Encontrar el límite de un cociente

Encontrar el límite de una función expresado como cociente puede ser más complicado. A menudo necesitamos reescribir la función algebraicamente antes de aplicar las propiedades de un límite. Si el denominador se evalúa a 0 cuando aplicamos las propiedades de un límite directamente, debemos reescribir el cociente en una forma diferente. Un enfoque es escribir el cociente en forma factorizada y simplificar.

Ejemplo$\PageIndex{4}$: Evaluating the Limit of a Quotient by Factoring

Evaluar\[\lim \limits_{x \to 2} (\frac{x^2−6x+8}{x−2}). \nonumber \]

Solución

Factorizar cuando sea posible, y simplificar.

\[\begin{align} \lim \limits_{x \to 2} (\dfrac{x^2−6x+8}{x−2}) &= \lim \limits_{x \to 2}(\dfrac{(x−2)(x−4)}{x−2}) && \text{Factor the numerator.} \\ & = \lim \limits_{x \to 2}(\dfrac{\cancel{(x−2)}(x−4)}{\cancel{x−2}}) && \text{Cancel the common factors.} \\ &= \lim \limits_{x \to 2}(x−4) && \text{Evaluate.} \\ & =2−4=−2 \end{align} \nonumber \]

Análisis

Cuando el límite de una función racional no puede evaluarse directamente, las formas factorizadas del numerador y denominador pueden simplificarse a un resultado que pueda ser evaluado.

Aviso, la función

\[f(x)=\dfrac{x^2−6x+8}{x−2} \nonumber \]

es equivalente a la función

\[f(x)=x−4,x≠2. \nonumber \]

Observe que el límite existe aunque la función no esté definida en$x = 2$.

Ejercicio$\PageIndex{4}$

Evalúe el siguiente límite:\[\lim \limits_{x \to 7} \left( \dfrac{x^2−11x+28}{7−x} \right) . \nonumber \]

Solución

$−3$

Ejemplo$\PageIndex{5}$: Evaluating the Limit of a Quotient by Finding the LCD

Evaluar\[\lim \limits_{x \to 5} \left( \dfrac{\frac{1}{x}−\frac{1}{5}}{x−5} \right) . \nonumber \]

Solución

Encuentra la LCD para los denominadores de los dos términos en el numerador, y convierte ambas fracciones para tener la LCD como denominador.

Análisis

Al determinar el límite de una función racional que tiene términos sumados o restados ya sea en el numerador o denominador, el primer paso es encontrar el denominador común de los términos sumados o restados; luego, convertir ambos términos para tener ese denominador, o simplificar la función racional multiplicando numerador y denominador por el mínimo denominador común. Después comprueba si el numerador y denominador resultantes tienen algún factor común.

Ejercicio$\PageIndex{5}$:

Evaluar\[\lim \limits_{x \to −5} \left( \dfrac{\frac{1}{5}+\frac{1}{x}}{10+2x} \right). \nonumber \]

Solución

$−\frac{1}{50}$

cómo: Dado un límite de una función que contiene una raíz, usar un conjugado para evaluar

Si el cociente dado no está en$(\frac{0}{0})$ forma indeterminada, evalúe directamente.
De lo contrario, reescribe la suma (o diferencia) de dos cocientes como un solo cociente, usando el mínimo denominador común (LCD).
Si el numerador incluye una raíz, racionaliza el numerador; multiplica el numerador y el denominador por el conjugado del numerador. Recordemos que$a±\sqrt{b}$ son conjugados.
Simplificar.
Evaluar el límite resultante.

Ejemplo$\PageIndex{6}$: Evaluating a Limit Containing a Root Using a Conjugate

Evaluar\[ \lim \limits_{x \to 0} \left( \dfrac{\sqrt{25−x} −5}{x} \right) . \nonumber \]

Solución

\[\begin{align} \lim \limits_{x \to 0} \left( \dfrac{\sqrt{25−x}−5}{x} \right) &= \lim \limits_{x \to 0} \left( \dfrac{(\sqrt{25−x}−5)}{x}⋅\frac{(\sqrt{25−x}+5)}{(\sqrt{25−x}+5)} \right) && \text{Multiply numerator and denominator by the conjugate.} \\ &= \lim \limits_{x \to 0} \left( \dfrac{(25−x)−25}{x(\sqrt{25−x}+5)} \right) && \text{Multiply: } (\sqrt{25−x} −5)⋅(\sqrt{25−x}+5)=(25−x)−25. \\ & = \lim \limits_{x \to 0} \left( \dfrac{−\cancel{x}}{\cancel{x}(25−x+5)} \right) && \text{Combine like terms.} \\ & =\lim \limits_{x \to 0} \left( \dfrac{−\cancel{x}}{\cancel{x}(\sqrt{25−x}+5)} \right) && \text{Simplify }\dfrac{−x}{x}=−1. \\ & =\dfrac{−1}{\sqrt{25−0}+5} && \text{Evaluate.} \\ & =\dfrac{−1}{5+5}=−\dfrac{1}{10} \end{align} \nonumber \]

Análisis

Al determinar un límite de una función con una raíz como uno de dos términos donde no podemos evaluar directamente, piense en multiplicar el numerador y denominador por el conjugado de los términos.

Ejercicio$\PageIndex{6}$

Evalúe el siguiente límite:$\lim \limits_{h \to 0} \left( \dfrac{\sqrt{16−h}−4}{h} \right) $.

Solución

$−\frac{1}{8}$

Ejemplo$\PageIndex{7}$: Evaluating the Limit of a Quotient of a Function by Factoring

Evaluar\[\lim \limits_{x \to 4} \left( \frac{4−x}{\sqrt{x−2}} \right). \nonumber \]

Solución

\[\begin{align} \lim \limits_{x \to 4} (\dfrac{4−x}{\sqrt{x}−2}) & = \lim \limits_{x \to 4} (\dfrac{(2+\sqrt{x})(2−x)}{\sqrt{x}−2}) && \text{Factor.} \\ &= \lim \limits_{x \to 4} ( \dfrac{(2+\sqrt{x})(\cancel{2−\sqrt{x}})}{−\cancel{(2−\sqrt{x})}}) && \text{Factor −1 out of the denominator. Simplify.} \\ & = \lim \limits_{x \to 4}−(2+x) && \text{Evaluate.} \\ &=−(2+ \sqrt{4}) \\ &=−4 \end{align} \nonumber \]

Análisis

Multiplicar por un conjugado expandiría el numerador; buscar en su lugar factores en el numerador. Cuatro es un cuadrado perfecto para que el numerador esté en la forma

\[a^2−b^2 \nonumber \]

y puede ser factorizado como

\[(a+b)(a−b). \nonumber \]

Ejercicio$\PageIndex{7}$

Evalúe el siguiente límite:\[\lim \limits_{x \to 3} \left( \frac{x−3}{\sqrt{x}−\sqrt{3} }\right). \nonumber \]

Solución

$2\sqrt{3}$

cómo: Dado un cociente con valores absolutos, evaluar su límite

Intente factorizar o encontrar la pantalla LCD.
Si no se puede encontrar el límite, elija varios valores cercanos y a ambos lados de la entrada donde la función esté indefinida.
Utilice la evidencia numérica para estimar los límites en ambos lados.

Ejemplo$\PageIndex{8}$: Evaluating the Limit of a Quotient with Absolute Values

Evaluar\[\lim \limits_{x \to 7} \frac{|x−7|}{x−7}. \nonumber \]

Solución

La función está indefinida en$x=7$, por lo que intentaremos valores cercanos a 7 desde la izquierda y la derecha.

Límite izquierdo:\[\frac{|6.9−7|}{6.9−7}=\frac{|6.99−7|}{6.99−7}=\frac{|6.999−7|}{6.999−7}=−1 \nonumber \]

Límite derecho:\[\frac{|7.1−7|}{7.1−7}=\frac{|7.01−7|}{7.01−7}=\frac{|7.001−7|}{7.001−7}=1 \nonumber \]

Dado que los límites izquierdo y derecho no son iguales, no hay límite.

Ejercicio$\PageIndex{8}$

Evaluar\[ \lim \limits_{x \to 6^+} \frac{6−x}{| x−6 |}. \nonumber \]

Solución

Conceptos clave

Las propiedades de los límites se pueden utilizar para realizar operaciones sobre los límites de las funciones en lugar de las funciones mismas. Ver Ejemplo.
El límite de una función polinómica se puede encontrar encontrando la suma de los límites de los términos individuales. Ver Ejemplo y Ejemplo.
El límite de una función que se ha elevado a una potencia equivale a la misma potencia del límite de la función. Otro método es la sustitución directa. Ver Ejemplo.
El límite de la raíz de una función es igual a la raíz correspondiente del límite de la función.
Una manera de encontrar el límite de una función expresado como cociente es escribir el cociente en forma factorizada y simplificar. Ver Ejemplo.
Otro método para encontrar el límite de una fracción compleja es encontrar la LCD. Ver Ejemplo.
Un límite que contiene una función que contiene una raíz puede evaluarse usando un conjugado. Ver Ejemplo.
Los límites de algunas funciones expresadas como cocientes se pueden encontrar por factorización. Ver Ejemplo.
Una forma de evaluar el límite de un cociente que contiene valores absolutos es mediante el uso de evidencia numérica. Configurarlo por partes también puede ser útil. Ver Ejemplo.

Glosario

propiedades de límites: una colección de teoremas para encontrar límites de funciones mediante la realización de operaciones matemáticas en los límites

Constante, k	\(\lim \limits_{x \to a} k=k \)
Tiempos constantes de una función	\(\lim \limits_{x \to a} [k⋅f(x)]=k \lim \limits_{x \to a} f(x)=kA\)
Suma de funciones	\(\lim \limits_{x \to a} [f(x)+g(x)]= \lim \limits_{x \to a}f(x)+ \lim \limits_{x to a} g(x)=A+B\)
Diferencia de funciones	\(\lim \limits_{x \to a} [f(x)−g(x)]= \lim \limits_{x \to a} f(x)− \lim \limits_{x \to a} g(x)=A−B\)
Producto de funciones	\( \lim \limits _{x \to a}[f(x)⋅g(x)]= \lim \limits _{x \to a}f(x)⋅ \lim \limits_{x \to a} g(x)=A⋅B\)
Cociente de funciones	\(\lim \limits _{x \to a} \frac{f(x)}{g(x)}= \frac{\lim \limits _{x \to a}f(x) }{\lim \limits _{x \to a}g(x)}=\frac{A}{B},B≠0\)
Función elevada a un exponente	\(\lim \limits _{x \to a}[f(x)]^n=[\lim \limits _{x \to ∞}f(x)]^n=A^n\), donde\(n\) es un entero positivo
n ésima raíz de una función, donde n es un entero positivo	\(\lim \limits _{x \to a}f(x) \sqrt[n]{f(x)} = \sqrt[n]{ \lim \limits _{x \to a}[ f(x) ]}=\sqrt[n]{A}\)
Función polinomial	\( \lim \limits _{x \to a} p(x)=p(a)\)