19: Inversiones Financieras
- Page ID
- 67868
Objetivos de aprendizaje
Después de completar este capítulo, debe ser capaz de: (1) distinguir entre inversiones financieras e inversiones de capital; (2) reconocer los diferentes tipos de inversiones financieras; y (3) evaluar los diferentes tipos de inversiones financieras utilizando modelos de valor presente (PV) desarrollados en capítulos anteriores.
Para lograr tus metas de aprendizaje, debes completar los siguientes objetivos:
- Distinguir entre inversiones financieras e inversiones no financieras.
- Aprenda cómo se pueden usar las herramientas fotovoltaicas para analizar las inversiones financieras utilizando métodos similares a los utilizados al comparar inversiones no financieras.
- Aprender a distinguir entre objetivos financieros y no financieros.
- Conozca el papel de los corredores, distribuidores e intermediarios financieros en los mercados de valores.
- Aprende a valorar valores sin riesgo como los depósitos a plazo.
- Conoce por qué Albert Einstein calificó al interés compuesto “el mayor descubrimiento matemático de todos los tiempos”.
- Conocer la naturaleza de los vínculos y las variables que determinan su valor.
- Conoce cómo las tasas impositivas afectan el valor de las inversiones financieras.
Introducción
En su sentido más amplio, invertir significa renunciar a algo en el presente por algo de mayor valor en el futuro. Las inversiones, en lo que invertimos, pueden diferir mucho. Pueden ir desde boletos de lotería y parcelas funerarias hasta bonos municipales y acciones corporativas. Es útil organizar estas inversiones en dos categorías generales: real y financiera. Las inversiones de capital, o reales, implican el intercambio de dinero por inversiones no financieras que producen servicios como servicios de almacenamiento de edificios, extracción de servicios de tractores y crecimiento de servicios desde tierra. Las inversiones financieras implican el intercambio de dinero en el presente para un pago de dinero futuro. Las inversiones financieras incluyen depósitos a plazo, bonos y acciones.
Este capítulo aplica los modelos fotovoltaicos desarrollados anteriormente a las inversiones financieras. Las grandes corporaciones y otras organizaciones empresariales requieren inversiones financieras de un gran número de pequeños inversionistas para proporcionar fondos para la operación y el crecimiento. El cobro de estos fondos sería imposible si cada inversionista estuviera obligado a ejercer una función gerencial sobre ellos. Además, la recaudación de fondos de inversión de un gran número de pequeños inversionistas sería imposible a menos que se les pudiera garantizar la seguridad de la inversión y la responsabilidad limitada. Se han diseñado varias inversiones financieras para superar estos y otros obstáculos de inversión.
El mercado en el que se negocian las inversiones financieras se denomina mercado de valores o mercado financiero. Las actividades en los mercados financieros son facilitadas por corredores, distribuidores e intermediarios financieros. Un corredor actúa como agente para inversionistas en los mercados de valores. El corredor de valores reúne a dos partes para obtener los mejores términos posibles para su cliente y es compensado por una comisión. Un distribuidor, a diferencia de un corredor, compra y vende valores para su propia cuenta. Así, un distribuidor también se convierte en inversionista. De manera similar, los intermediarios financieros (por ejemplo, bancos, empresas de inversión y compañías de seguros) desempeñan un papel importante en el flujo de fondos de ahorradores a inversionistas finales. El intermediario adquiere la propiedad de los fondos prestados o invertidos por los ahorradores, modifica el riesgo y la liquidez de estos fondos, y luego presta los fondos a prestatarios individuales o invierte en diversos tipos de activos financieros.
Numerosos libros discuten los arreglos institucionales asociados al comercio de valores. En este capítulo, el enfoque no en los detalles de la negociación en el mercado de valores sino en cómo valorar las inversiones financieras o los valores.
Valuación de Valores sin Riesgo
Los precios de las inversiones financieras, al igual que otros precios, se determinan en mercados, mercados financieros. Las características de los mercados financieros, sin embargo, pueden diferir significativamente dependiendo del tipo de inversión financiera negociada. Común a todos los mercados financieros, sin embargo, es que los precios se establecen al igualar los deseos de compradores y vendedores. Además, en equilibrio no hay exceso de demanda ni exceso de oferta. Sin embargo, el equilibrio no significa que todos los posibles compradores y vendedores estén de acuerdo en que el precio de una inversión sea igual a su valor. Sólo significa que se ha encontrado un precio que, en cierto sentido, equilibra los diferentes objetivos de compradores y vendedores.
Depósitos a tiempo. Los depósitos a plazo son dinero depositado en una institución bancaria por un período de tiempo determinado. La principal diferencia entre los diferentes tipos de depósitos a plazo es su liquidez. En términos generales, cuanto menos líquidos son los depósitos de tiempo, mayor es su rendimiento.
La forma más líquida de depósitos a tiempo se conoce a veces como depósitos “on call”. Los depósitos a la vista pueden ser retirados en cualquier momento y sin previo aviso ni penalización alguna. Ejemplos de depósitos a la vista incluyen dinero depositado en una cuenta de ahorros o de cheques en un banco. Otro tipo de depósito a plazo es un certificado de depósito (CDs). Cuando los CD maduran, pueden ser retirados o pueden ser retenidos por otro término. Los CD generalmente se consideran líquidos porque son negociables y pueden redescontarse cuando el titular necesita algo de liquidez.
Algunos depósitos a plazo deben retenerse hasta su vencimiento o sufrir sanciones por retiro anticipado. La tasa de rendimiento de estos depósitos a plazo es mayor que los depósitos a la vista debido a que el requisito de que los depósitos se mantengan por un plazo designado le da al banco la capacidad de invertir en productos financieros que obtengan mayores rendimientos. Además, el rendimiento de los depósitos a plazo es generalmente inferior al rendimiento promedio de las inversiones a largo plazo en productos de mayor riesgo como acciones y algunos bonos. Algunos bancos ofrecen cuentas de depósito a tiempo vinculadas al mercado que ofrecen rendimientos potencialmente más altos al tiempo que garantizan el capital.
Las inversiones en depósitos a plazo pueden consistir en una inversión única o una serie de depósitos. Lo que todos los depósitos a plazo tienen en común es que el pago o pagos están compuestos hasta alguna fecha de finalización, momento en el que se retiran parcial o totalmente. Así, nuestro interés no está en el valor presente de los pagos sino en su valor futuro. El precio determinado por el mercado en el caso de las inversiones financieras es la tasa compuesta a la que los depósitos a tiempo ganan intereses. Por lo general, la tasa compuesta de interés ganada por los depósitos a plazo es baja, en parte porque proporcionan una liquidez casi perfecta, especialmente para los depósitos a plazo para los que no hay penalización ni costo de transacción asociados con el retiro de fondos.
Anualidades ordinarias y anualidades adeudadas. Anteriormente describimos una anualidad como una serie temporal de pagos constantes realizados o recibidos al final de cada periodo. Las anualidades pagadas y percibidas al término de un periodo se denominan anualidades ordinarias. Las anualidades pagadas (o recibidas) al inicio de cada periodo se denominan pagos adeudados por anualidades.
Para ilustrar una anualidad adeudada, considere una serie de depósitos R realizados cada periodo, el primero ocurriendo en el presente. Escribimos el valor futuro V n de la serie temporal de depósitos R compuestos a tasa r para retiro en el periodo n como:
(19.1)

Tenga en cuenta que el primer depósito de tiempo R se compone por n períodos, y es igual en valor a su valor compuesto al inicio del período n. De igual manera, el segundo pago se compone para n — 1 período y es igual a su valor compuesto al inicio del período n. Finalmente, el último pago es hecho al inicio del periodo n — 1 y se compone una vez para encontrar su valor compuesto al inicio del periodo n.
Para ilustrar, supongamos que un ahorrador deposita un pago de $90 (PMT) al inicio de cada periodo por n = 10 periodos. Si los depósitos son compuestos a una tasa de r = 2%, ¿qué cantidad hay disponible para retiro al inicio del periodo 10? Resolvemos este problema usando Excel en la Tabla 19.1. Tenga en cuenta que para indicar los pagos vencidos de anualidad al inicio del periodo, se cambia “tipo” en la función FV de valor futuro de Excel de su default de cero a 1. En lugar de PV en la ecuación, ingresamos un espacio en blanco cerrado con una coma.
Cuadro 19.1. El Valor Futuro
de 10 Pagos Anuales de $90 Compuesto al 2% Mesa
Abierta 19.1 en Microsoft Excel
| B6 | Función: | =FV (B4, B5, B3,, B2) | |
| A | B | C | |
| 1 | El valor futuro de 10 pagos vencidos de anualidad de $90 compuesto al 2% | ||
| 2 | tipo | 1 | |
| 3 | PMT | ($90.00) | |
| 4 | tasa | 0.02 | |
| 5 | n | 10 | |
| 6 | FV | 1,005.18 | “=FV (tasa, nper, pmt, [pv], tipo) |
| 7 | PV | 0 | |
Lo que determinan nuestros cálculos es que al inicio del décimo periodo, tenemos $1,005.18 disponibles. Sin embargo, hay varias otras preguntas interesantes que podríamos responder usando nuestras fórmulas de Excel. Por ejemplo, podríamos querer saber cuántos períodos se requerirían para tener $2,000 disponibles en alguna fecha futura. Continuando con las entradas ya realizadas en Excel, agregamos lo siguiente:
Cuadro 19.2. Encontrar el
número de pagos vencidos de anualidad requeridos para obtener un valor futuro de
$2,000
Open Table 19.2 en Microsoft Excel
| B5 | Función: | =NPER (B4, B3, B6, B2) | |
| A | B | C | |
| 1 | Cantidad de pagos anuales de $90 adeudados de anualidad compuestos al 2% requeridos para ganar un FV de $2,000 | ||
| 2 | tipo | 1 | |
| 3 | PMT | ($90.00) | |
| 4 | tasa | 0.02 | |
| 5 | n | 29.69347722 | “=NPER (tasa, pmt, FV, tipo) |
| 6 | FV | $2,000 | |
| 7 | PV | 0 | |
Podríamos estar interesados en conocer la inversión periódica requerida para tener $2,000 disponibles en 10 años si las inversiones se compusieron en 2%. La fórmula de Excel requerida se representa en la Tabla 19.3.
Cuadro 19.3. Encontrar el pago adeudado de
anualidad requerido para obtener un valor futuro de $2,000 en 10
años Tabla
abierta 19.3 en Microsoft Excel
| B3 | Función: | =PMT (B4, B5, B7, B6, B2) | |
| A | B | C | |
| 1 | Pago de vencimiento de anualidad anual compuesto al 2% Requerido para ganar un FV de $2,000 en 10 años. | ||
| 2 | tipo | 1 | |
| 3 | PMT | ($179.07) | “=PMT (tasa, nper, PV, FV, tipo) |
| 4 | tasa | 0.02 | |
| 5 | n | 10 | |
| 6 | FV | $2,000 | |
| 7 | PV | 0 | |
Para alcanzar la meta de ahorro de $2,000 en 10 años a una tasa compuesta del 2% requeriría un pago periódico en un depósito a tiempo al inicio de cada periodo igual a $179.07.
Interés Compuesto
La magia de componer. Se afirma que Albert Einstein calificó al interés compuesto “el mayor descubrimiento matemático de todos los tiempos”. Es probable que ningún otro concepto en finanzas tenga más importancia para los inversionistas que lo que a veces se llama la “maravilla del interés compuesto”. El interés compuesto genera ganancias no solo sobre el monto original ahorrado o invertido, sino que también genera ganancias sobre los intereses sobre las ganancias, y lo hace período tras período. Otra forma de describir este proceso es decir que el interés compuesto genera ganancias sobre la inversión y ganancias reinvertidas de la inversión. Para darse cuenta del poder del interés compuesto se requieren dos cosas: la reinversión de las ganancias y el tiempo.
Nuestros cálculos previos confirman la importancia del interés compuesto. En 10 pagos de $90 acumulamos un valor futuro de $1,005.18. Al realizar 8.57 pagos adicionales, duplicamos nuestro valor futuro. Encontramos un efecto similar cuando aumentamos los pagos de préstamos y observamos disminuciones significativas en el plazo. Al encontrar el efecto del aumento en los pagos del préstamo en los términos del préstamo, calculamos la elasticidad del plazo del préstamo con respecto al tamaño del pago del préstamo. De igual manera, podemos encontrar el impacto de un incremento en el plazo de ahorro periódico sobre los valores futuros (FV). Nos referimos a esta elasticidad como la elasticidad FV con respecto al término. La derivación de la elasticidad FV respecto al término se encuentra en Derivación 19.1 al final de este capítulo. La aproximación discreta a la elasticidad FV con respecto a n es:
(19.2)
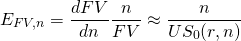
El Cuadro 19.4 proporciona estimaciones de elasticidad para tasas y términos de reinversión alternativos.
Cuadro 19.4. Valores presentados de elasticidad E FV, n = N/us 0 (r, n)
| n | r = .01 | r = .03 | r = .05 | r = .08 | r = .10 | r = .15 |
| 1 | 1.00% | 1.03% | 1.05% | 1.08% | 1.10% | 1.15% |
| 3 | 1.02% | 1.06% | 1.10% | 1.16% | 1.21% | 1.31% |
| 5 | 1.03% | 1.09% | 1.15% | 1.25% | 1.32% | 1.49% |
| 10 | 1.05% | 1.17% | 1.30% | 1.49% | 1.63% | 1.99% |
| 20 | 1.08% | 1.34% | 1.60% | 2.04% | 2.35% | 3.20% |
| 30 | 1.16% | 1.53% | 1.95% | 2.66% | 3.18% | 4.57% |
| 60 | 1.34% | 2.17% | 3.17% | 4.85% | 6.02% | 9.00% |
Una pregunta relacionada con una respuesta más intuitiva es ¿cuánto tiempo se tarda en duplicar, triplicar o cuadruplicar la inversión? La derivación para la ecuación que responde a esta pregunta se puede encontrar en Derivación 19.2 al final de este capítulo.
Sea m el número de veces que uno quiere multiplicar su FV obtenido en el periodo n. Dejar que nm sea igual al periodo en el que se realiza el último depósito. Entonces podemos encontrar el número de periodos (nm — n) requeridos para aumentar el FV original en m veces. La fórmula que se encuentra en la Derivación 19.2 se proporciona a continuación:
(19.3)
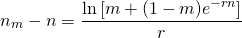
Para ilustrar, vamos r = .1, n = 5, y m = 2. El número de periodos requeridos para duplicar el FV de la inversión original es igual a:
(19.4)
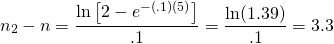
En este ejemplo, una inversión consistente en 5 pagos iguales compuestos al 10% podría duplicarse en 3.3 pagos adicionales. Y la inversión podría triplicarse en:
(19.5)
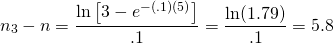
El segundo ejemplo ilustra el poder del interés compuesto. A partir de 5 periodos de inversión, en 3.3 periodos más el FV de la inversión se duplicó y en 5.8 períodos adicionales el FV de la inversión original se triplicó.
Finalmente, concluimos esta sección construyendo el Cuadro 19.5 que demuestra el poder del interés compuesto. Las celdas de la tabla indican el tiempo requerido para duplicar, triplicar y cuadruplicar una inversión inicial para tasas de reinversión de 1%, 3%, 5% y 10%.
Cuadro 19.5. Periodos requeridos para duplicar, triplicar o cuadruplicar el FV de una inversión consistente en 5 pagos iguales asumiendo tasas de reinversión alternativas.
| Tasas de reinversión alternativas | Número de periodos de tiempo requeridos para aumentar el FV de la inversión original m veces | ||
| m = 2 (el doble del FV original) | m = 3 (el triple del FV original) | m = 4 (cuadruplicar el FV original) | |
| 1% | 4.8 | 9.3 | 13.7 |
| 3% | 4.4 | 8.2 | 11.6 |
| 5% | 4.0 | 7.3 | 10.2 |
| 10% | 3.3 | 5.8 | 7.8 |
La regla del 72 se aproxima a la cantidad de tiempo que lleva duplicar su inversión a una tasa de rendimiento determinada. Para aplicar la regla, se divide la tasa de retorno por 72. Por ejemplo, suponga que invierte $1000 a una tasa de interés del 5%. Tomaría 14.4 años (72/5) para duplicar su inversión a $2000.
Bonos
Un bono es un activo financiero que se negocia frecuentemente en los mercados financieros. Los bonos representan créditos de deuda sobre los activos e ingresos de la entidad emisora del bono. El valor de un bono es igual al valor presente de su flujo de efectivo futuro (interés y principal) descontados a una tasa de interés apropiada. Los bonos suelen tener una fecha de vencimiento conocida, momento en el que el titular del bono recibe el valor nominal o nominal del bono. Los bonos son únicos porque su valor de redención o liquidación es fijo. Los montos típicos de canje son $1,000 o $10,000.
Considera el siguiente ejemplo. Supongamos que un bono se puede comprar a un precio de V 0 (una salida de efectivo inicial) y redimirse n periodos después a un valor en efectivo de V n, una entrada de efectivo al tenedor del bono. Además, supongamos que el bono no genera retorno de efectivo salvo cuando se vende. Además, supongamos que la tasa de descuento antes de impuestos es r por ciento. Ignorando cualquier consecuencia fiscal, el VPN de este bono es la suma de la salida de efectivo más el valor presente de la entrada de efectivo.
(19.6)
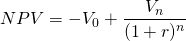
Quienes compran bonos pueden querer calcular el “rendimiento” de un bono, que es la tasa de descuento que equipara el valor presente del flujo de efectivo del bono a su valor actual de mercado, la tasa interna de rendimiento (TIR) del bono. Si, por ejemplo, el valor de mercado del bono es de 321.97 dólares y su flujo de caja de $1,000 ocurre al final del año 10, entonces el rendimiento del bono, o su TIR, es del 12 por ciento.
(19.7)
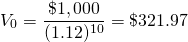
Consideremos ahora el efecto de los impuestos. Primero, supongamos que los impuestos sobre las ganancias de capital son pagados por el comprador de bonos a tasa T g y los impuestos sobre la renta se pagan a la tasa T. El VAN después de impuestos del bono se calcula ajustando la tasa de descuento a su equivalente después de impuestos y restando del valor de liquidación del bono, el impuesto sobre las ganancias de capital:
(19.8)
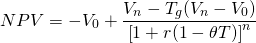
donde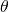 se define el coeficiente de ajuste fiscal en el Capítulo 11. Si el VAN
en la Ecuación\ ref {19.5} es cero entonces
se define el coeficiente de ajuste fiscal en el Capítulo 11. Si el VAN
en la Ecuación\ ref {19.5} es cero entonces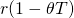 es la TIR después de impuestos del bono. Para encontrar la tasa impositiva efectiva establecemos el
VAN igual a cero en las ecuaciones (19.8) y (19.6) para que el flujo de
caja antes de impuestos descontado por la TIR antes de impuestos en la Ecuación\ ref {19.6}
sea igual al flujo de caja después de impuestos descontado por la TIR después de impuestos
en la Ecuación\ ref {19.8}. Entonces resolvemos para
es la TIR después de impuestos del bono. Para encontrar la tasa impositiva efectiva establecemos el
VAN igual a cero en las ecuaciones (19.8) y (19.6) para que el flujo de
caja antes de impuestos descontado por la TIR antes de impuestos en la Ecuación\ ref {19.6}
sea igual al flujo de caja después de impuestos descontado por la TIR después de impuestos
en la Ecuación\ ref {19.8}. Entonces resolvemos para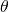 eso hace que las dos ecuaciones sean iguales. El resultado es:
eso hace que las dos ecuaciones sean iguales. El resultado es:
(19.9)

Para ilustrar usando los números de nuestro
ejemplo anterior, dejemos que la TIR antes de impuestos sea igual al 12%, que
V 0 sea igual a 321.97 dólares, que V n
sea igual a $1,000, y que el impuesto sobre la renta y el impuesto a las ganancias patrimoniales
T y T g ambos igual al 15 por ciento. A continuación
haciendo las sustituciones apropiadas en la Ecuación\ ref {19.6}
encontramos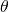 igual a:
igual a:
(19.10)

Para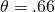 la tasa impositiva efectiva se reduce de 0.15 a (.66) (0.15) =
0.10.
la tasa impositiva efectiva se reduce de 0.15 a (.66) (0.15) =
0.10.
En el ejemplo, recién terminado, pudimos
deducir una solución de forma cerrada para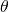 .
En la mayoría de los casos, las soluciones de forma cerrada son muy difíciles de obtener.
Sin embargo, en la mayoría de los casos prácticos que involucran
estimaciones numéricas, aún podemos encontrar estimaciones para la tasa impositiva efectiva
y las IRR después de impuestos. Demostraremos el enfoque empírico para
encontrar tasas impositivas efectivas en la siguiente sección.
.
En la mayoría de los casos, las soluciones de forma cerrada son muy difíciles de obtener.
Sin embargo, en la mayoría de los casos prácticos que involucran
estimaciones numéricas, aún podemos encontrar estimaciones para la tasa impositiva efectiva
y las IRR después de impuestos. Demostraremos el enfoque empírico para
encontrar tasas impositivas efectivas en la siguiente sección.
Cupones y bonos
La mayoría de los bonos, además de las ganancias (o pérdidas) de capital, proporcionan pagos de “cupón” (intereses). El número y la cantidad de los pagos del cupón alterarán el VAN así como el precio del bono. Por lo general, la tasa de cupón r c es un porcentaje del valor de redención del bono.
El VAN antes de impuestos de un bono con n pagos de cupón es:
(19.11)
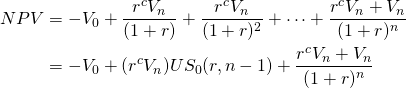
Para ilustrar, supongamos que un inversionista quiere encontrar
el precio máximo de oferta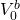 para un bono de $1,000 de tres años si ofrece pagos de cupón de
r c V n = (.05) (1,000) = $50, y
r = 10%. Luego usando la Ecuación\ ref {19.11} y estableciendo NPV
igual a cero, encuentra el precio máximo de puja
para un bono de $1,000 de tres años si ofrece pagos de cupón de
r c V n = (.05) (1,000) = $50, y
r = 10%. Luego usando la Ecuación\ ref {19.11} y estableciendo NPV
igual a cero, encuentra el precio máximo de puja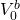 igual a:
igual a:
(19.12)
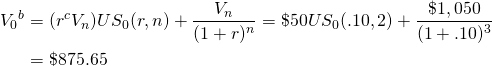
Los impuestos, por supuesto, afectan el VPN de los bonos con pagos de cupones. Sólo ahora, los impuestos pueden o no ser pagados sobre los pagos de cupones y ganancias de capital. Por ejemplo, los pagos de cupones de muchos bonos municipales no están gravados sino que sus ganancias patrimoniales están gravadas. Las exenciones fiscales, por supuesto, elevan el precio máximo de oferta y los NPV de los bonos para todos los inversionistas pero especialmente para los inversionistas de mayor categoría fiscal. El valor presente después de impuestos del bono con pagos de cupón exentos de impuestos se escribe como:
(19.13)
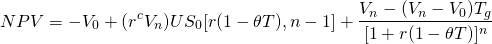
Para ilustrar, supongamos que un inversionista quiere encontrar
el precio máximo de oferta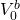 para un bono de $1,000 de tres años si ofrece pagos de cupón de
r c V n = (.05) (1,000) = $50 y
r = 10% y paga ganancias de capital e impuestos sobre la renta a
tasa de 10%. Luego usando la Ecuación\ ref {19.13} y estableciendo el VAN igual
a cero, encontramos el precio máximo de puja
para un bono de $1,000 de tres años si ofrece pagos de cupón de
r c V n = (.05) (1,000) = $50 y
r = 10% y paga ganancias de capital e impuestos sobre la renta a
tasa de 10%. Luego usando la Ecuación\ ref {19.13} y estableciendo el VAN igual
a cero, encontramos el precio máximo de puja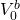 para el bono cuyo precio máximo de puja anterior se calculó igual
a $875.65:
para el bono cuyo precio máximo de puja anterior se calculó igual
a $875.65:
(19.14)
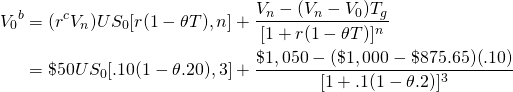
En la aplicación de la Ecuación\ ref {19.13}, la tasa de
descuento fue la IRR, porque fue la tasa de descuento la que
resultó en un VPN igual a cero. Introducimos impuestos en el
flujo de caja, pero no conocemos la tasa efectiva de descuento después de impuestos que
establecería el VAN igual a cero. Tenemos que resolver para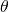 eso se ajustará la tasa de descuento para impuestos en la
misma magnitud que fueron el flujo de caja ajustado por impuestos. Para Ecuación\ ref {19.13},
encontramos la TIR después de impuestos usando Excel:
eso se ajustará la tasa de descuento para impuestos en la
misma magnitud que fueron el flujo de caja ajustado por impuestos. Para Ecuación\ ref {19.13},
encontramos la TIR después de impuestos usando Excel:
Cuadro 19.6. Cómo encontrar la tabla
abierta 19.6 de IRR
después de impuestos en Microsoft Excel
| B6 | Función: | =IRR (B2:B5) | |
| A | B | C | |
| 1 | Encontrar la TIR después de impuestos | ||
| 2 | Precio máximo de puja de Bond | -875.65 | |
| 3 | primer pago de cupón | 50 | |
| 4 | segundo pago de cupón | 50 | |
| 5 | Valor de salvamento (1000) + pago de cupón | 1037.6 | |
| 6 | TIR | 9.59% | “=TIR (B2: B5) |
El cálculo de la TIR de 9.59% equivale a la
TIR después de impuestos de 9.59% en comparación con la TIR antes de impuestos del 10%. Podemos encontrar
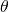 y la tasa impositiva efectiva estableciendo
y la tasa impositiva efectiva estableciendo
(19.15)
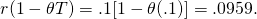
De la ecuación anterior encontramos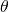 = .41. Así, la tasa impositiva efectiva es (.2) (.41) = 8% —muy inferior a
la tasa real del impuesto sobre la renta del 20%.
= .41. Así, la tasa impositiva efectiva es (.2) (.41) = 8% —muy inferior a
la tasa real del impuesto sobre la renta del 20%.
Para revisar el proceso, comenzamos resolviendo
el precio máximo de oferta del bono. Esto requirió que la tasa de
descuento declarada fuera la TIR antes de impuestos para el bono. Entonces razonamos de la
siguiente manera. Si el precio máximo de oferta es el mismo ya sea calculado
sobre una base antes o después de impuestos, entonces el efecto de los impuestos sobre el flujo de
efectivo, en este caso el impuesto sobre las ganancias de capital, debe tener el mismo
efecto sobre la tasa de descuento. Por lo tanto, requerimos que el
precio máximo de oferta en el modelo después de impuestos sea la misma oferta máxima determinada en
el modelo antes de impuestos y resuelta para la TIR después de impuestos y el coeficiente de
ajuste fiscal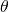 .
.
Acciones Comunes
A diferencia de los bonos, las acciones ordinarias no tienen ni un rendimiento fijo ni un costo fijo. El valor terminal de los bonos suele ser fijo, pero el valor terminal de las acciones depende del valor de mercado de las acciones en el momento de la venta. El capital social generado por la venta de acciones es una alternativa al capital de deuda generado por la venta de bonos. También es un medio para compartir el riesgo entre numerosos inversionistas.
Las acciones ofrecen importantes beneficios tanto para los accionistas como para las empresas que emiten las acciones. Los accionistas tienen la oportunidad de ser propietarios de los principales negocios del mundo con la consecuente participación en las ganancias mientras que su responsabilidad se limita a sus inversiones. Además, la propiedad de acciones los libera de las responsabilidades de toma de decisiones en la gestión de la empresa, aunque las acciones ordinarias permiten a sus propietarios votar por directores y a veces otros asuntos de importancia que enfrenta la compañía.
Los propietarios de acciones reciben pagos de dividendos sobre sus acciones, generalmente trimestralmente. El monto de los dividendos pagados sobre acciones es determinado por el consejo de administración de una corporación. Las políticas de dividendos de la junta directiva pueden influir en los tipos de acciones que emiten y en los tipos de inversionistas que atraen.
La pregunta relevante para un posible comprador de acciones es ¿cuál es el precio máximo de oferta para una acción en particular? Si r es la tasa de descuento nominal, y R 1, R 2, son dividendos proyectados pagados sobre la acción en los periodos 1, 2,, el precio máximo de puja para la acción es:
(19.16)
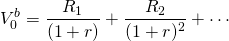
El modelo anterior asume una vida infinita. Este supuesto es congruente con el principio de “vida de la inversión” discutido en el Capítulo 8 porque para conocer el valor terminal de la acción, V n, debemos conocer el valor de los dividendos en periodos (n + 1), (n + 2),. Conocer todos los dividendos futuros convierte el problema en uno en el que el número de periodos es igual a la vida de la firma.
Una forma simplificada de Ecuación\ ref {19.16} es posible si los dividendos esperados R 1, R2, son reemplazados por su equivalente de anualidad esperada R. Entonces podemos escribir:
(19.17)
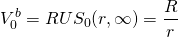
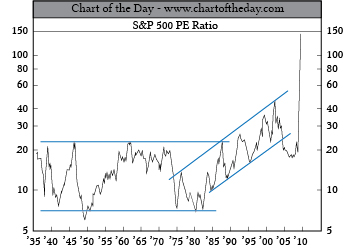
Y r, la TIR de la acción, es R/V 0. Así, con dividendos constantes a largo plazo de $100 y la acción valorada en $1000, la tasa de retorno es del 10%. Otra relación importante derivada de la Ecuación\ ref {19.16} es lo que comúnmente se conoce como la relación precio-ganancias, V 0/R = 1/r que a menudo se ve como el indicador de las irregularidades financieras en el mercado financiero. Ratios precio-ganancias superiores a lo habitual pueden indicar lo que se ha llamado “exuberancia irracional” para la inversión. Ratios precio-ganancias inferiores a lo habitual pueden indicar que la inversión está infravalorada.
Por último, el capital de deuda debe ser reembolsado independientemente de las fortunas financieras del negocio. Sin embargo, el retorno a los accionistas depende críticamente del desempeño de la compañía. Esto hace que el análisis de VPN de las inversiones en acciones esté sujeto a una incertidumbre considerable.
Figura 19.1. La relación S&P 500 PE alcanza máximos históricos.
Resumen y Conclusiones
Este capítulo ha introducido conceptos relacionados con las inversiones financieras que implican intercambios de dinero a lo largo del tiempo. En relación con las inversiones financieras, la atención se centra en la cantidad de inversión disponible en algún periodo de tiempo futuro. Encontramos el FV de una inversión financiera por capitalización de intereses. Como demostramos en la Tabla 19.1, el poder de la composición es realmente asombroso. Por lo tanto, el consejo para la mayoría de los inversionistas es invertir temprano y continuamente, y luego dejar crecer la inversión.
Los depósitos a tiempo representan una importante oportunidad de inversión financiera. Estos difieren principalmente en su liquidez, los que son menos líquidos también son los que tienen mayores rendimientos. Los bonos son una clase importante de inversión financiera. A diferencia de la mayoría de las demás inversiones financieras, su valor de liquidación es fijo. Lo que no es fijo es su precio de compra que se establece en el mercado y depende de su rendimiento, su TIR esperado.
Uno de los aspectos interesantes de los bonos es la forma en que se gravan. A menudo, cuando los bonos son emitidos por municipios y algunas otras instituciones, reciben consideraciones fiscales especiales. En el extremo ni sus pagos de cupones ni sus ganancias patrimoniales están gravados. En otras circunstancias, las ganancias de capital están gravadas y los pagos de cupones no lo son. Independientemente, una pregunta importante es cómo afectan las provisiones fiscales especiales provistas de algunos bonos a sus IRR después de impuestos. Si bien la TIR efectiva después de impuestos a veces se puede encontrar en una expresión formulaica, a menudo son demasiado complicadas para expresarse en una solución de forma cerrada pero se pueden encontrar numéricamente calculando las IRR antes y después de impuestos.
Por último, solo introdujimos el concepto de acciones comunes. Las inversiones en acciones comunes se discuten con mayor frecuencia en el contexto o análisis de riesgos e incluyen discusiones sobre muchas alternativas de estrategias de respuesta al riesgo. Una discusión más completa sobre las inversiones en acciones está fuera del alcance de este texto de gestión financiera.
Preguntas
- Invertir significa renunciar a algo en el presente por algo de valor en el futuro. ¿Puedes describir tres de tus inversiones personales más importantes? Describa lo que sacrificó, incluido el dinero y el tiempo, y describa sus rendimientos futuros esperados.
- Describir la diferencia entre inversiones reales y financieras. Describa también cómo pueden diferir los ajustes de inversión para inversiones reales y financieras.
- ¿Describir las principales características de los tipos alternativos de depósitos a plazo? ¿Cuáles son las tasas de rendimiento que ofrecen actualmente los principales bancos o cooperativas de ahorro y crédito sobre tipos alternativos de depósitos a plazo?
- Supongamos que un ahorrador invierte $65 en un depósito a tiempo al inicio de cada periodo por 10 periodos. Si los depósitos son compuestos a una tasa del 4%, ¿qué cantidad hay disponible para retiro al inicio del periodo 11?
- Supongamos que una pareja joven que ahora está alquilando un departamento quiere invertir en su propia casa. El rango de precios promedio de su vivienda deseada es de aproximadamente $250,000. Si realizan depósitos mensuales en una cuenta de depósito a plazo al inicio del periodo por 5 años y sus depósitos obtienen una tasa compuesta APR del 3%, ¿cuál sería el tamaño requerido de su depósito mensual para pagar el 20% requerido del pago inicial del precio de su vivienda ($50,000)? Si deseaban guardar el anticipo requerido en tres años, ¿cuál sería el tamaño requerido de sus depósitos mensuales?
- Se afirma que Albert Einstein calificó al interés compuesto “el mayor descubrimiento matemático de todos los tiempos”. ¿Qué tiene la composición que es tan importante que haría tal afirmación? ¿Estás de acuerdo? Si es así, ¿por qué? Si no estás de acuerdo, ¿cuál sería un descubrimiento matemático alternativo de mayor importancia?
- Describir con palabras el significado de la elasticidad del valor futuro de una inversión con respecto a su término. Después se calcula la elasticidad del valor futuro de una inversión compuesta a una tasa de TAE de 4% por 12 periodos. ¿Cómo cambiaría la medida de elasticidad si la tasa compuesta se incrementara a 7%? ¿Se puede explicar la dirección del cambio?
- Encuentre el número de periodos requeridos para duplicar el valor futuro de una inversión compuesta por 5 periodos a tasas de reinversión alternativas de 2%, 4% y 8%.
- Un inversionista desea ahorrar 10.000 dólares. Si la tasa compuesta es de 3% mensual y el inversionista planea ahorrar $200 al inicio de cada mes, ¿cuántos meses se requerirán para que el inversionista alcance su meta de ahorro de 10,000 dólares? Una vez que se alcanza el objetivo de ahorro, ¿cuántos meses de adición se requerirán para que la ahorradora duplique la cantidad ahorrada si ahorra a la misma tasa?
- Considera un bono a 8 años con un valor nominal de $10,000. Si el precio de compra del bono es de $4,250, ¿cuál es el rendimiento del bono? (Ignorar la influencia de los impuestos.)
- ¿Cuál es la relación entre el rendimiento del bono (su TIR) y el precio de compra del bono? ¿Qué esperarías que sucediera con el precio de compra del bono si aumentara el rendimiento esperado del bono? Por favor explique.
- En el ejemplo que ilustra la Ecuación\ ref {19.8}, se encontró que la tasa impositiva efectiva para un comprador de bonos era igual a θT = .66 (.15) = 10%. Por favor recalcule la tasa impositiva efectiva en el ejemplo suponiendo que la tasa impositiva sobre las ganancias de capital sea solo del 50% de la tasa del impuesto sobre la renta Es decir, si la tasa impositiva sobre las ganancias de capital es de 7.5%, ¿cuál es la tasa impositiva efectiva del comprador de bonos? ¿Cómo cambia la reducción de la tasa impositiva efectiva la TIR efectiva después de impuestos de la firma?
- Considera la ecuación:
(Q19.1)
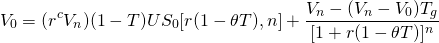
donde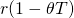 está la TIR después de impuestos de un bono.
está la TIR después de impuestos de un bono.
A continuación, considere la ecuación:
(Q19.2)
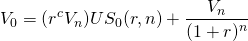
donde r es la TIR antes de impuestos del bono.
Entonces supongamos que
V 0 = $500, V n = $1000,
r c V n = .04 ($1,000) = $40, T
= 20%, y T g = 10%. Encuentre las IRR antes y
después de impuestos utilizando las dos ecuaciones descritas en esta pregunta
y los valores enumerados. Después, utilice las IRR antes y después de impuestos
para encontrar el valor del coeficiente de ajuste impositivo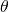 .
.
- Compara la regla del 72 con el tiempo real requerido para duplicar tu inversión.
Derivación 19.1.
La derivación de la elasticidad del valor futuro (FV) con respecto al término:
La elasticidad de FV con respecto a n se define como:
(19.i)
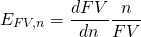
El valor futuro de n pagos compuestos a tasa r es igual a:
(19.ii)
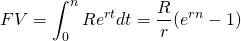
Y la derivada de FV con respecto a n es:
(19.iii)
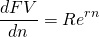
Sustituyendo en la fórmula de elasticidad encontramos:
(19.iv)
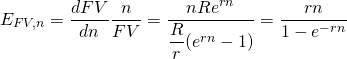
La aproximación discreta de la elasticidad de FV con respecto a n es:
(19.v)
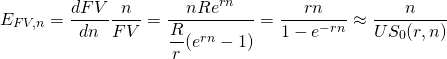
Derivación 19.2.
Derivar la fórmula para calcular el número de periodos para duplicar el FV de una inversión n periodo reinvertida a una tasa de interés de r%.
Para comenzar, el valor futuro (FV) de una inversión de n periodo R compuesta a tasa r es igual a:
(19.vi)
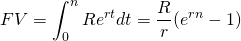
Ahora m veces el FV de la inversión original se establece igual a la misma inversión compuesta por periodos nm:
(19.vii)
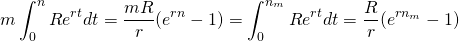
y simplificando al igualar las dos ecuaciones integradas anteriores encontramos:
(19.viii)
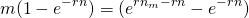
Luego resolviendo la diferencia entre (nm — n), encontramos el tiempo que lleva aumentar el FV de la inversión original en el periodo n por m veces.
(19.ix)