8.1: Teoría de enlace de valencia
- Page ID
- 1862
Habilidades para desarrollar
- Describir la formación de enlaces covalentes en términos de superposición orbital atómica.
- Definir y dar ejemplos de enlaces σ y π
Tal como sabemos, la teoría científica es una explicación fuertemente apoyada para las leyes naturales observadas o grandes cuerpos de datos experimentales. Para que una teoría sea aceptada, debe explicar los datos experimentales y poder predecir el comportamiento. Por ejemplo, la teoría VSEPR ha ganado una gran aceptación porque predice formas moleculares tridimensionales que son consistentes con los datos experimentales recopilados para miles de moléculas diferentes. Sin embargo, la teoría VSEPR no proporciona una explicación del enlace químico.
Existen teorías exitosas que describen la estructura electrónica de los átomos. Podemos usar la mecánica cuántica para predecir las regiones específicas alrededor de un átomo donde es probable que se encuentren los electrones: una forma esférica para un orbital, una forma de mancuerna para un orbital p, y así sucesivamente. Sin embargo, estas predicciones solo describen los orbitales alrededor de los átomos libres. Cuando los átomos se unen para formar moléculas, los orbitales atómicos no son suficientes para describir las regiones donde se ubican los electrones en la molécula. Una comprensión más completa de las distribuciones de electrones requiere un modelo que pueda explicar la estructura electrónica de las moléculas. Una teoría popular sostiene que se forma un enlace covalente cuando un par de electrones es compartido por dos átomos y es atraído simultáneamente por los núcleos de ambos átomos. En las siguientes secciones, discutiremos cómo dichos enlaces se describen mediante la teoría de enlace de valencia y la hibridación.
La teoría de enlace de valencia describe un enlace covalente como la superposición de orbitales atómicos medio llenos (cada uno contiene un solo electrón) que produce un par de electrones compartidos entre los dos átomos unidos. Decimos que los orbitales en dos átomos diferentes se superponen cuando una porción de un orbital y una porción de un segundo orbital ocupan la misma región del espacio. Según la teoría del enlace de valencia, se produce un enlace covalente cuando se cumplen dos condiciones:
- un orbital en un átomo se superpone a un orbital en un segundo átomo y
- los electrones individuales en cada orbital se combinan para formar un par de electrones.
La atracción mutua entre un par de electrones cargados negativamente y los dos núcleos cargados positivamente de los átomos sirve para unir físicamente los dos átomos a través de una fuerza llamada un enlace covalente. La fuerza del enlace covalente depende del grado de superposición de los orbitales involucrados. Los orbitales que se superponen forman enlaces que son más fuertes que los enlaces que se superponen menos.
La energía de un sistema depende de cuanto los orbitales se superponen. La Figura \(\PageIndex{1}\) ilustra como la suma de las energías de dos átomos de hidrógeno (la curva colorada) cambia a medida que se acercan entre sí. Cuando los átomos están muy separados no hay superposición, y por convención ponemos la suma de las energías a cero. A medida que los átomos se muevan más cercas, sus orbitales empiezan a superponerse. Cada electrón comienza a sentir la atracción del núcleo en el otro átomo. Además, los electrones comienzan a repelerse entre sí, al igual que los núcleos. Si los átomos siguen separados, las atracciones son un poco más fuertes que las repulsiones, y la energía del sistema disminuye. (Un enlace comienza a formarse). A medida que los átomos se acercan, la superposición aumenta, por lo que la atracción de los núcleos por los electrones continúa aumentando (al igual que las repulsiones entre los electrones y entre los núcleos). A cierta distancia específica entre los átomos, que varía según los átomos involucrados, la energía alcanza su valor más bajo (más estable). Esta distancia óptima entre los dos núcleos unidos es la distancia de enlace entre los dos átomos. El enlace es estable porque en este punto, las fuerzas atractivas y repulsivas se combinan para crear la configuración de energía más baja posible. Si la distancia entre los núcleos disminuyera aún más, las repulsiones entre los núcleos y las repulsiones como electrones confinados en una proximidad más cercana se volverían más fuertes que las fuerzas de atracción. La energía del sistema aumentaría (haciendo que el sistema se desestabilizara), como se muestra en el extremo izquierdo de la Figura \(\PageIndex{1}\).
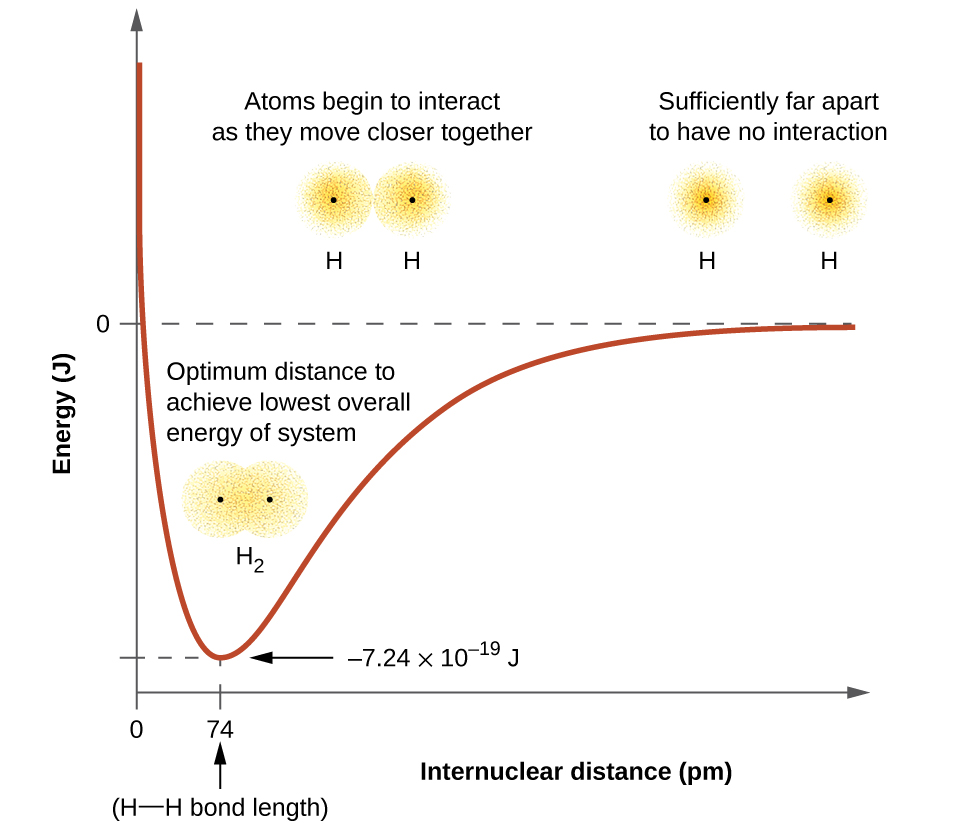
La energía de enlace es la diferencia entre la energía mínima (que ocurre a la distancia de enlace) y la energía de los dos átomos separados. Esta es la cantidad de energía liberada cuando se forma el enlace. Por el contrario, se requiere la misma cantidad de energía para romper el enlace. Para la molécula \(H_2\) que se muestra en la Figura \(\PageIndex{1}\), a la distancia de enlace de 74 pm el sistema es \(7.24 \times 10^{−19}\), más bajo en energía que los dos átomos de hidrógeno separados. Esto puede parecer como un número pequeño. Sin embargo, sabemos por nuestra descripción anterior de la termoquímica que las energías de enlace a menudo se discuten por mol. Por ejemplo, requiere \(7.24 \times 10^{−19}\; J\) para romper un enlace H - H, pero se necesita \(4.36 \times 10^5\; J\) para romper 1 mol de H - H enlaces. En la Tabla \(\PageIndex{1}\) se muestra una comparación de algunas longitudes de enlace y energías. Podemos encontrar muchos de estos enlaces en una variedad de moléculas, y esta tabla nos da valores promedio. Por ejemplo, romper el primer enlace C - H en CH4 requiere 439.3 kJ/mol, mientras que romper el primer enlace C - H en \(\ce{H-CH2C6H5}\) (un diluyente de pintura común) requiere 375.5 kJ/mol.
| Enlace | Longitud (pm) | Energía (kJ/mol) | Enlace | Longitud (pm) | Energía (kJ/mol) | |
|---|---|---|---|---|---|---|
| H–H | 74 | 436 | C–O | 140.1 | 358 | |
| H–C | 106.8 | 413 | \(\mathrm{C=O}\) | 119.7 | 745 | |
| H–N | 101.5 | 391 | \(\mathrm{C≡O}\) | 113.7 | 1072 | |
| H–O | 97.5 | 467 | H–Cl | 127.5 | 431 | |
| C–C | 150.6 | 347 | H–Br | 141.4 | 366 | |
| \(\mathrm{C=C}\) | 133.5 | 614 | H–I | 160.9 | 298 | |
| \(\mathrm{C≡C}\) | 120.8 | 839 | O–O | 148 | 146 | |
| C–N | 142.1 | 305 | \(\mathrm{O=O}\) | 120.8 | 498 | |
| \(\mathrm{C=N}\) | 130.0 | 615 | F–F | 141.2 | 159 | |
| \(\mathrm{C≡N}\) | 116.1 | 891 | Cl–Cl | 198.8 | 243 |
Además de la distancia entre dos orbitales, la orientación de los orbitales también afecta su superposición (a excepción de los dos orbitales, que son esféricamente simétricos). Una superposición más grande es posible cuando los orbitales están orientados de tal manera que se superponen en una línea directa entre los dos núcleos. La figura \(\PageIndex{2}\) ilustra esto para dos orbitales p de átomos diferentes; la superposición es mayor cuando los orbitales se superponen de extremo a extremo en lugar de en ángulo.
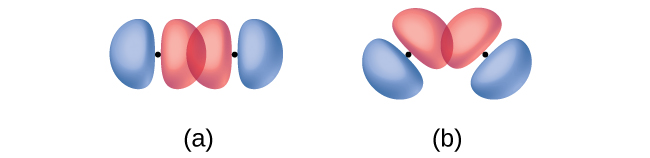
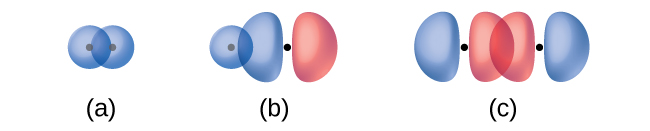
La superposición de dos orbitales s (como en H2), la superposición de un orbital s y p (como en HCl), y la superposición de extremo a extremo de dos orbitales p (como en Cl2) todos producen enlaces sigma (σ enlaces), como se ilustra en la Figura \(\PageIndex{3}\). Un enlace σ es un enlace covalente en el que la densidad de los electrones se concentra en la región a lo largo del eje internuclear; es decir, una línea entre los núcleos pasaría por el centro de la región de superposición. Los enlaces simples en las estructuras de Lewis se describen como enlaces σ en la teoría del enlace de valencia.
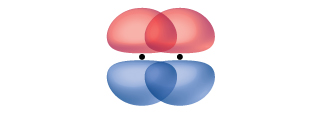
Un enlace pi (enlace π) es un tipo de enlace covalente que resulta por la superposición de dos orbitales p, como se ilustra en la Figura \(\PageIndex{4}\). En un enlace π, las regiones de superposición orbital se encuentran en lados opuestos del eje internuclear. A lo largo del eje, hay un nodo, es decir, un plano sin probabilidad de encontrar un electrón.
Ya que todos los enlaces simples son enlaces σ, los enlaces múltiples consisten en enlaces σ y π. Como sugieren las estructuras de Lewis, O2 contiene un doble enlace y N2 contiene un triple enlace. El doble enlace consiste en un enlace σ y un enlace π, y el enlace triple consiste en un enlace σ y dos enlaces π. Entre dos átomos, el primer enlace formado siempre será un enlace σ, pero solo puede haber un enlace σ en cualquier ubicación a un tiempo. En cualquier enlace múltiple, habrá un enlace σ, y los uno o dos enlaces restantes serán enlaces π. Estos enlaces se describen con más detalle más adelante en este capítulo.
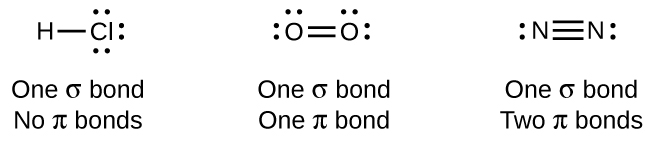
Como se ve en la Tabla \(\PageIndex{1}\), un enlace sencillo de carbono-carbono promedio es 347 kJ/mol, mientras que en un enlace doble de carbono-carbono, el enlace π aumenta la resistencia del enlace a 267 kJ/mol. Agregar un enlace π adicional provoca un aumento de 225 kJ/mol. Podemos ver un patrón similar cuando comparamos otros enlaces de σ y π. Por lo tanto, cada enlace π individual es generalmente más débil que un enlace σ correspondiente entre los mismos dos átomos. En un enlace σ, hay un mayor grado de superposición orbital que en un enlace de π.
Ejemplo\(\PageIndex{1}\): Contando Enlaces de σ y π
Butadieno, C4H6, se usa para hacer caucho sintético. Identifique el número de enlaces σ y π que esta molécula contiene.
Butadiene
Solución
Hay seis enlaces σ C – H y un enlace σ C – C, para un total de siete de los enlaces simples. Hay dos enlaces dobles que tienen un enlace π además del enlace σ. Esto da un total de nueve enlaces σ y dos enlaces π en general.
Ejercicio \(\PageIndex{1}\)
Identifique cada ilustración como una representación de un enlace σ o π:
- superposición lado a lado de un orbital 4p y 2p
- superposición de extremo a extremo de un orbital 4p y 4p
- superposición de extremo a extremo de un orbital 4p y 2p

- Respuesta
-
(a) es un enlace π con un nodo a lo largo del eje que conecta los núcleos, mientras que (b) y (c) son enlaces σ que se superponen a lo largo del eje.
Resumen
La teoría del enlace de valencia describe el enlace como una consecuencia de la superposición de dos orbitales atómicos separados en átomos diferentes que crea una región con un par de electrones compartidos entre los dos átomos. Cuando los orbitales se superponen a lo largo de un eje que contiene los núcleos, se forma un enlace σ. Cuando se superponen de una manera que crea un nodo a lo largo de este eje, forman un enlace π.
Glosario
- superposición
- coexistencia de orbitales de dos átomos diferentes que comparten la misma región del espacio, lo que forma un enlace covalente
- nodo
- plano que separa diferentes lóbulos de los orbitales, donde la probabilidad de encontrar un electrón es cero
- enlace pi (enlace π)
- enlace covalente formado por superposición de orbitales atómicos de lado a lado; la densidad electrónica se encuentra en lados opuestos del eje internuclear
- enlace sigma (enlace σ)
- enlace covalente formado por la superposición de orbitales atómicos a lo largo del eje internuclear
- teoría del enlace de valencia
- Descripción de enlaces que involucran la superposición de orbitales atómicos para formar enlaces σ o π, dentro de los cuales se comparten pares de electrones
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


