14.6: La geometría del estado de transición de reacciones que implican enlaces pi
- Page ID
- 2424
In all of the reactions we have been studying throughout the past two chapters, there is an important consideration, which has been put off until now, concerning the three-dimensional geometry of the transition state. This section covers some very challenging material, so don't be discouraged if you don't understand everything at first - after your classroom instructor talks you through the main ideas, it will all make a lot more sense when you read through the section again. Throughout this discussion, it will be particularly important for you, in order to follow the three-dimensional arguments being put forward, to build models of the molecules involved. As you do this, be very careful to select the correct hybridization state for your carbon atoms - remember, sp3-hybridized carbons have tetrahedral bonding, while sp2-hybridized carbons are trigonal-planar.
14.6A: Transition state geometry of E2 reactions
We will start with some interesting observations about concerted (E2) elimination reactions from the organic laboratory. When cis-2-methylcyclohexyl bromide is treated with a strong base such as sodium ethoxide, two possible elimination products result.

When trans-2-methylcyclohexyl bromide is used, however, only one elimination product is observed - the product of elimination from the C6 side.
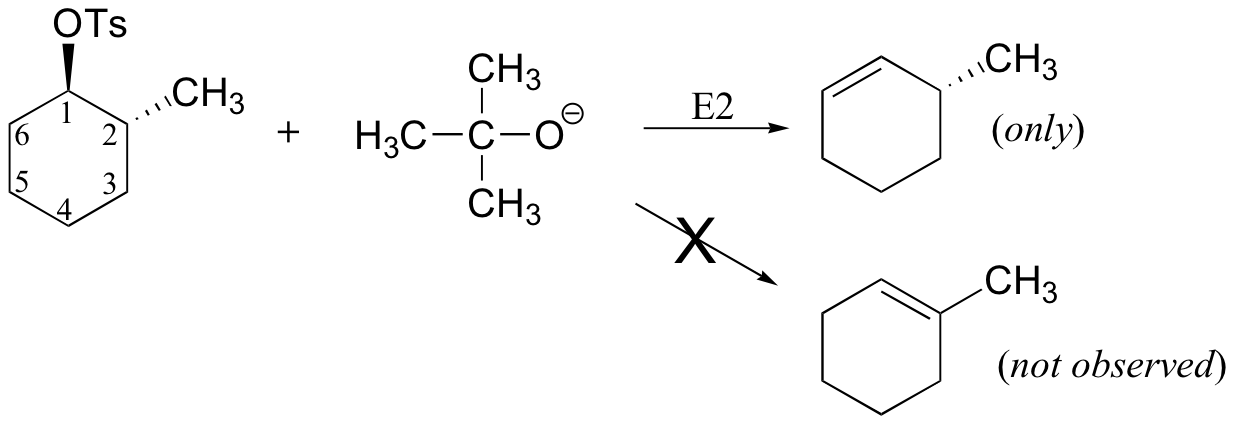
Why doesn't elimination occur from the C2 side?
To answer this question, we must carefully consider the transition state of a concerted (E2) elimination:
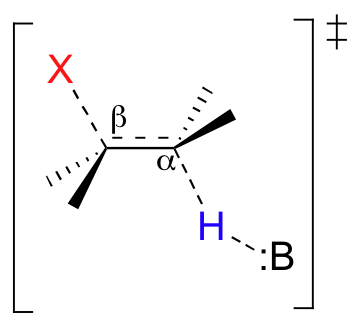
At the transition state, the hybridization on both the alpha and the beta carbons is changing from sp3 to sp2. As this happens, the sp3 orbitals of both the Cα-H sigma-bond and the Cβ-X sigma-bond become unhybridized p orbitals which hold two electrons (from the former Cα-H bond) in the new pi bond. In order to overlap and form a pi bond, these two p orbitals must be on the same plane. Thus, leading up to the transition state, the two sp3 orbitals must also be coplanar - in other words, for the concerted elimination to take place, the molecule must be in a conformation where the breaking Cα-H and Cβ-X bonds lie in the same plane.
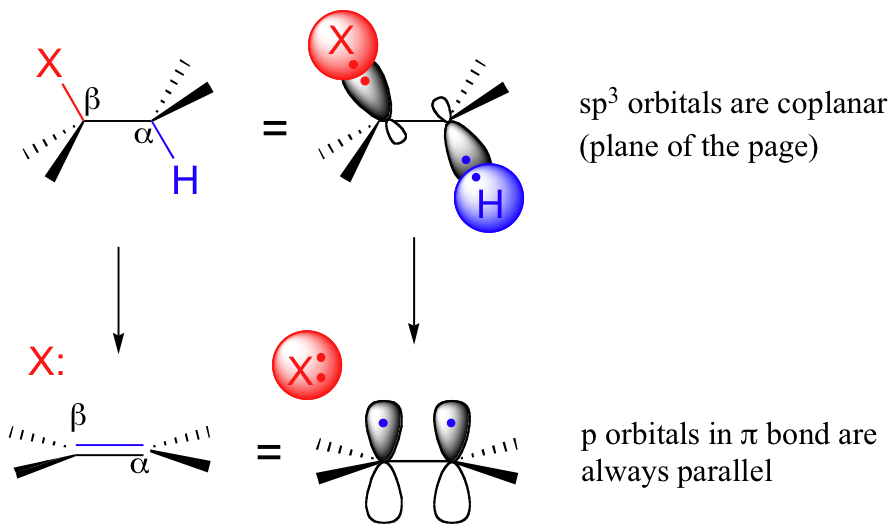
This occurs either when the two bonds are eclipsed (0o dihedral angle), or anti (180o dihedral angle).
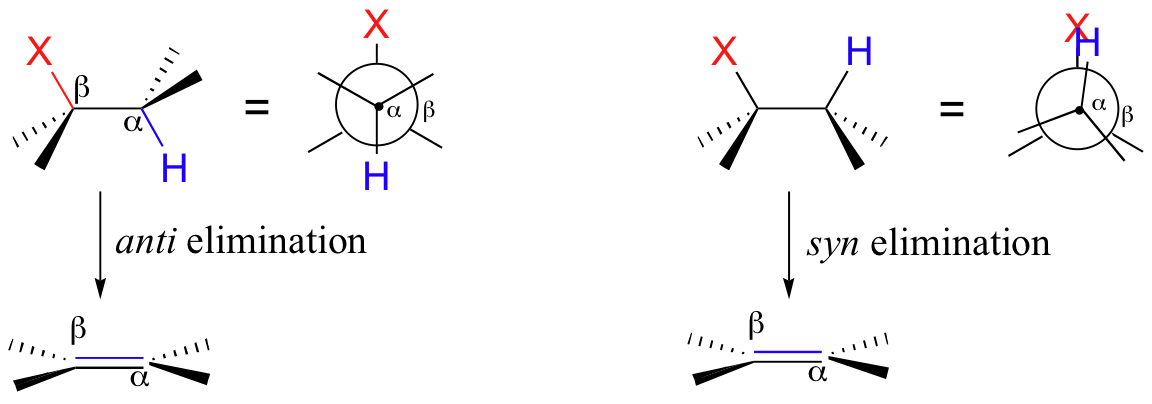
If the Cα-H bond and the Cβ-X bond are eclipsed, the elimination is syn, while if they are anti, the elimination is anti.
If the Cα-H bond and the Cβ-X bond are not coplanar, the elimination cannot take place until a conformational change occurs to put them in the same plane.
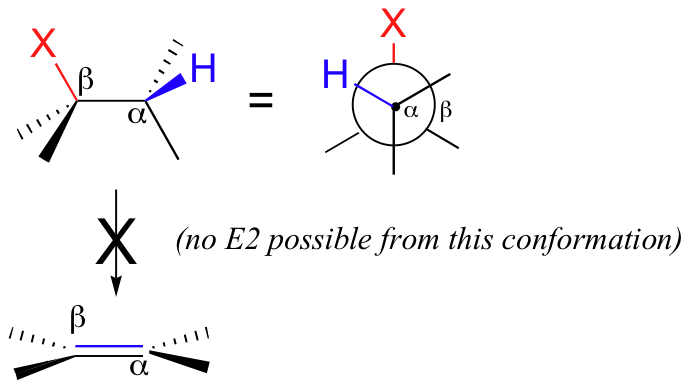
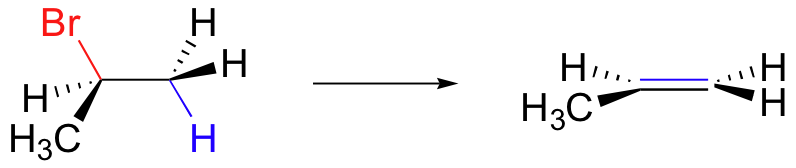
A molecule such as 2-bromopropane, therefore, can easily undergo E2 elimination - all that is required is for one of the six methyl protons to be eclipsed or anti to the bromine at the instant of proton abstraction.
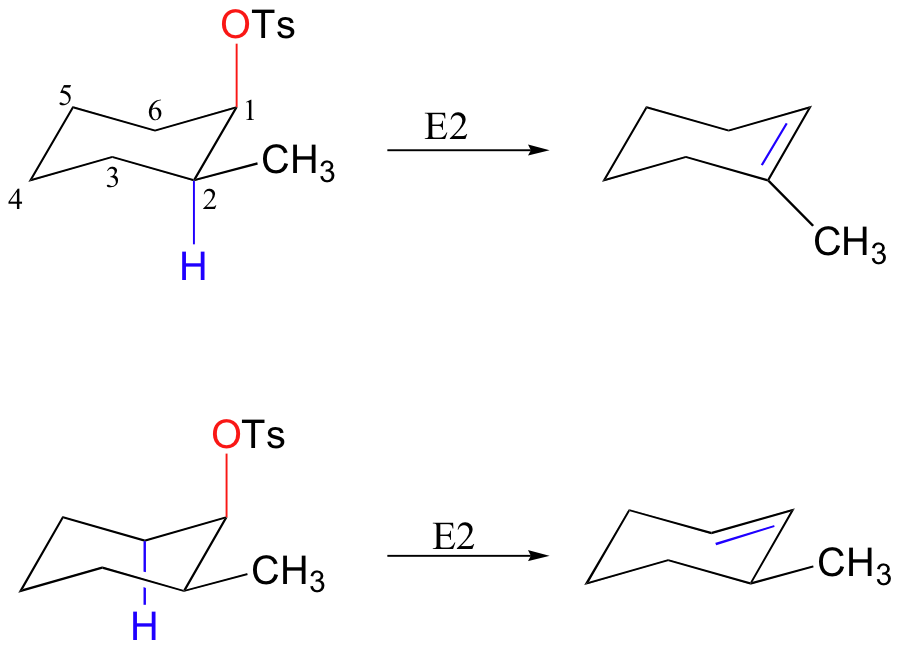
With a cyclic molecule such as cis-2-methylcyclohexyl tosylate, however, in order for a C6-H or C2-H bond to be parallel to the C1-Ts bond, the tosylate must be in an axial position (remember from section 3.2C that six-membered rings tend to adopt the chair conformation).
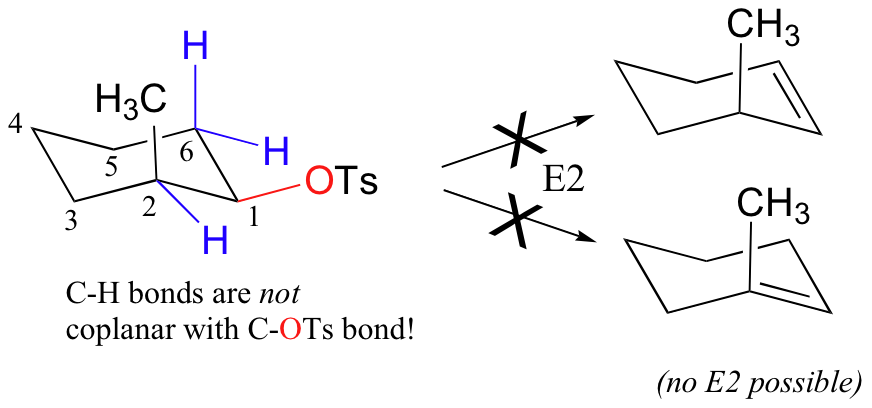
If the tosylate is in the equitorial position, it is impossible for an adjacent C-H bond to be parallel, and thus b-elimination is also impossible. The ring must 'flip' to the conformation in which the tosylate is in the higher energy axial position in order for an E2 elimination to take place.
What about trans-2-methylcyclohexyl tosylate - why is only one E2 product possible? If we draw the molecule in a chair conformation with the tosylate leaving group in the required axial position, the adjacent C2-Hb bond must be equitorial - and not coplanar with the C1-Ts bond.
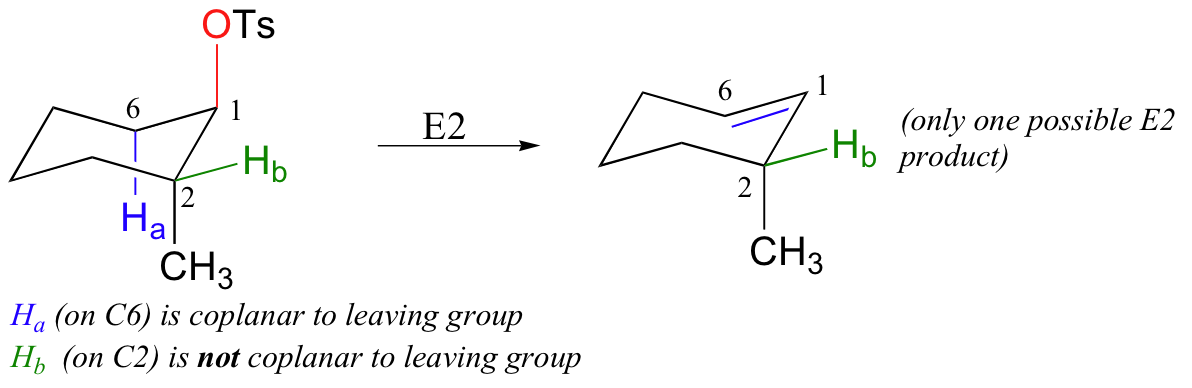
Thus, elimination can only occur from the C6 side, where one of the C6-H bonds is axial - and thus coplanar - with the C1-OTs bond.
14.6B: Transition state geometry of PLP-dependent reactions
PLP-dependent reactions provide another nice example of the stereochemical concepts discussed above. Consider, for example, the serine dehydratase reaction, a beta-elimination (section 14.4F). Serine loses it's alpha-proton in step 1, and the two electrons in this bond join the extended pi system of the PLP coenzyme. In order for this to occur, the Cα-H bond must be held by the enzyme at an angle that is parallel to the overlapping 2p orbitals in the pi system - in other words, approximately perpendicular to the planar PLP ring.

When the water leaves at Cβ (step 2), the breaking bond must be also be positioned perpendicular to the PLP plane. This allows the newly-formed pi bond between Cα and Cβ to join the extended pi system.
One of the most important ways that enzymes lower the activation energy of reactions like these is by binding the reacting molecules with the correct conformational geometry.


