6.3: Espectro de líneas y Modelo de Bohr
- Page ID
- 1936
Objetivo
-
Comprender la relación entre el espectro atómico y la estructura electrónica.
En 1900 Planck propone una expresión matemática que liga que la energía de la luz a su frecuencia, y que permite explicar el espectro continuo de radiación del cuerpo negro. El tema central de esta sección es el modelo atómico de Bohr, para el cual la idea de Planck tuvo gran importancia.
Espectro de línea
Aunque los objetos a elevada temperatura emiten radiación en un rango continuo de longitud de onda, se han observado otros tipos de emisiones. Por ejemplo, cuando una descarga eléctrica fluye por un tubo con hidrógeno gaseoso a baja presión, los átomos de hidrógeno resultantes de la disociación de H2 emiten luz roja. A diferencia de la radiación del cuerpo negro, el color de la luz emitida por los átomos de hidrógeno no depende en gran medida de la temperatura del tubo. Si la luz emitida atraviesa un prisma, solo ciertas líneas estrechas, correspondiendes a longitudes de onda definidas, son detectadas, en lugar de un rango continuo (Figura 6.3.1). La luz emitida por los átomos de hidrógeno es roja porque, de sus líneas características, la más intensa cae en la región roja del espectro visible, a 656 nm (Figura 6.3.1 b). Al reemplazar hidrógeno por sodio, se observa color amarillo dado por su línea más intensa en el espectro visible, a 589 nm.


Figura \(\PageIndex{1}\): Luz emitida por hidrógeno atómico. (a) Una muestra de átomos de hidrógeno excitados emite luz roja característica. (b) Cuando la luz
emitida por el hidrógeno atómico atraviesa un prisma, cuatro líneas características (violeta, azul, verde y roja) son observadas. La más intensa ocurre a 656 nm.
Hacia fin del siglo XIX se observaron espectros de emisión para diversos elementos, y presentaban un reto, ya que la física clásica no lograba modelarlos. Parte de la explicación se debe a la ecuación de Planck: solo se observan algunos valores de λ (o ν) en el espectro de líneas, lo que implica que solo algunos valores de energía eran posibles. Los niveles de energía del átomo de hidrógeno debían estar cuantizados; en otras palabras, solo estados con cierto valor de energía eran accesibles. Si el átomo de hidrógeno pudiera acceder a cualquier valor de energía, se observaría un espectro continuo.
En el año 1885, un profesor de matemática suizo, Johann Balmer (1825-1898), mostró que las frecuencias visibles del espectro de emisión del hidrógeno podían ajustarse por:
\[ \nu=constant\; \left ( \dfrac{1}{2^{2}}-\dfrac{1}{n^{^{2}}} \right ) \label{6.3.1}\]
donde n = 3, 4, 5, 6. En su honor, las líneas se denominaron líneas de Balmer. Años más tarde, el físico sueco Johannes Rydberg (1854-1919) expandió el resultado de Balmer. Rydberg encontró que:
\[ \dfrac{1}{\lambda }=\Re\; \left ( \dfrac{1}{n^{2}_{1}}-\dfrac{1}{n^{2}_{2}} \right ) \label{6.3.2}\]
donde \(n_1\) y \(n_2\) son enteros positivos, \(n_2 > n_1\). \( \Re \) es la constante de Rydberg, cuyo valor es 1.09737 × 107 m−1.
Johann Balmer (1825–1898)
A sus 60 años, y al tiempo que escribía el trabajo sobre las líneas espectrales que lo hizo famoso, Balmer era profesor de matemática para una escuela secundaria de mujeres en Suiza.
Balmer publicó solo un trabajo en el tópico, y se publicó cuando tenía 72 años.
Al igual que la ecuación de Balmer, la ecuación de Rydberg describe las longitudes de onda visibles en el espectro de emisión del hidrógeno (para n1 = 2, n2 = 3, 4, 5,…). Pero más importante, la ecuación de Rydberg también describe la longitud de onda de otras series de líneas: una en el ultravioleta (n1 = 1, n2 = 2, 3, 4,…) y una en el infrarrojo (n1 = 3, n2 = 4, 5, 6). Desafortunadamente, los científicos todavía no encontraban una relación con la estructura atómica.
Modelo de Bohr
En 1913 el físico Danés Niels Bohr (1885–1962; Premio Nobel de física, 1922) propuso un modelo teórico para el átomo de hidrógeno que explicaba su espectro de emisión (no de Bohr sino del hidrógeno). Para ello, asumió que el electrón se mueve alrededor del núcleo en órbitas circulares de cierto radio. Su antecesor era el modelo de Rutherford, que además de asumir movimiento circular de los electrones alrededor del núcleo, suponía que los electrones se mantenían enlazados al núcleo por atracción electrostática. Aunque ahora sabemos que la asunción de órbitas circulares era incorrecta, la gran idea de Bohr fue proponer que el electrón solo podía ocupar ciertas regiones del espacio (determinadas por el radio).
Utilizando mecánica clásica, Niels Bohr mostró que la energía de un electrón en una órbita particular es:
\[ E_{n}=\dfrac{-\Re hc}{n^{2}} \label{6.3.3}\]
donde \( \Re \) es la constante de Rydberg, h la constante de Planck, c es la velocidad de la luz, y n un entero positivo correspondiente al número asignado a la órbita (o período). n = 1 correponde a la órbita más cercana al núcleo; n = ∞ corresponde al nivel donde cesa la atracción del núcleo, y el radio de órbita es infinito (ver figura \(\PageIndex{2}\)). En este punto, el átomo ha sido separado en protón y electrón (ionizado).
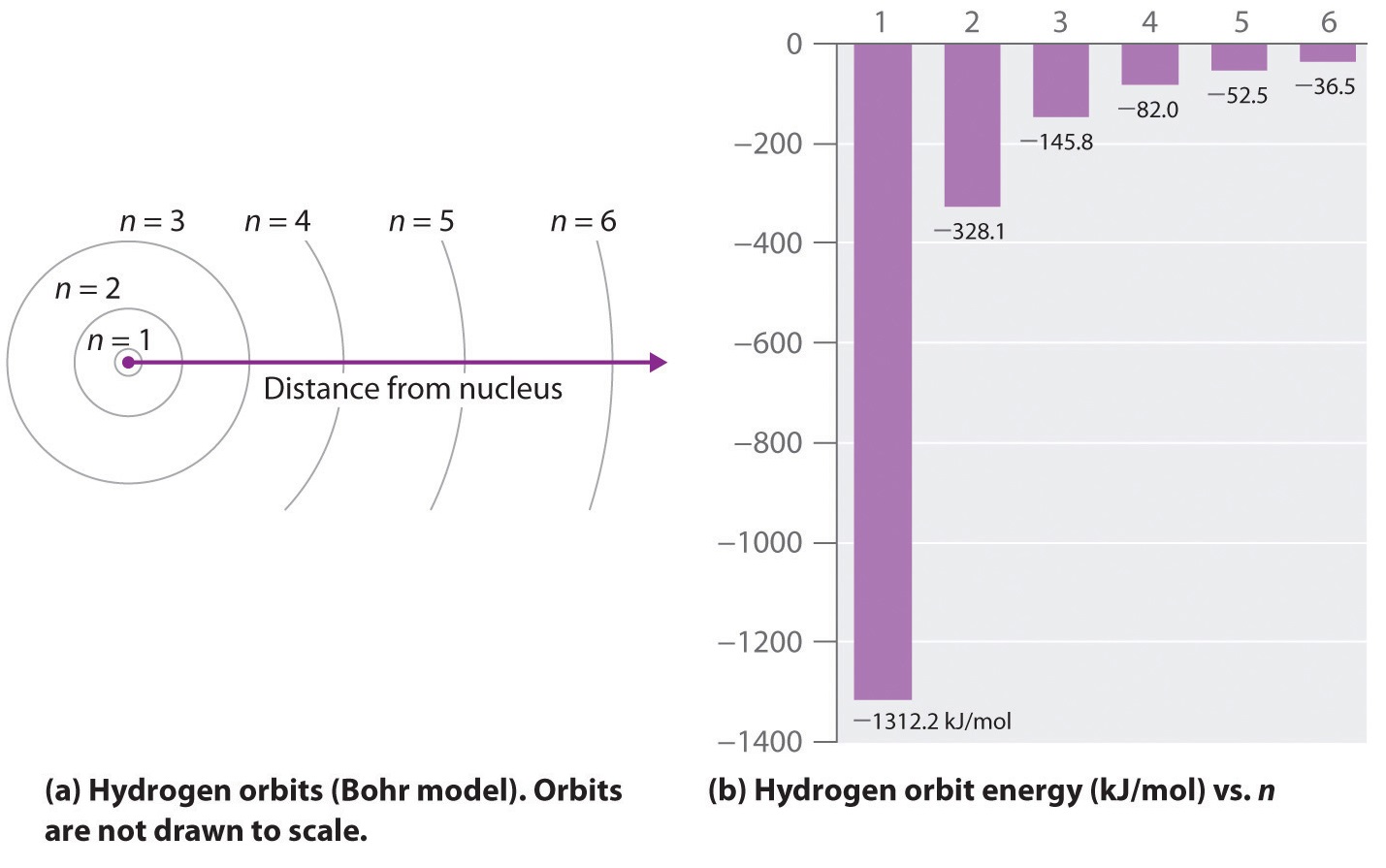
Figura \(\PageIndex{2}\): Modelo de Bohr del átomo de Hidrógeno. (a) La distancia órbita-núcleo incrementa con n. (b) La energía de la órbita se vuelve menos negativa (aumenta) al incrementar el número n.
Niels Bohr (1885–1962)
Durante la ocupación Nazi en Dinamarca, en la segunda guerra mundial, Bohr escapó a los Estados Unidos, donde se asoció al Proyecto de Energía Atómica.
En sus últimos años trabajó en la aplicación pacífica de la física atómica y cuestiones ligadas al desarrollo de armas nucleares.
El estado basal es el estado de menor energía de un átomo o molécula, y depende del arreglo de electrones en sus capas. La energía del átomo de hidrógeno se minimiza ubicando su electrón en la órbita de mínima energía (menor n y menor radio). Al incrementar n, incrementa el radio de la órbita, el electrón se aleja del protón y el arreglo es menos estable o de mayor energía (Figura 6.3.2a). El estado de menor energía o basal para el hidrógeno implica n=1 (ecuación \(\ref{6.3.3}\)); en consecuencia, si n>1 el estado posee mayor energía y denomina estado excitado. Cuando el átomo decae de un estado excitado al basal pierde energía emitiendo un fotón. La energía del fotón corresponde a la diferencia de energía entre los dos estados atómicos involucrados (Figura \(\PageIndex{3}\)), y explica las líneas espectrales observadas (Figura \(\PageIndex{1}\)).
Figura \(\PageIndex{3}\): Emisión lumínica del hidrógeno atómico. (a) Luz emitida cuando un electrón decae de una órbita con n mayor (mayor energía) a una con n menor
(menor energía). (b) Las líneas de Balmer se deben a transiciones de órbitas con n ≥ 3 a órbitas con n = 2. La diferencia de energía entre niveles se corresponde con la región visible del espectro electromagnético (luz).
La diferencia de energía (ΔE) entre cualesquiera dos órbitas o nivelesde energía está dada por \( \Delta E=E_{n_{1}}-E_{n_{2}} \) donde n1 es el estado final y n2 el inicial. Sustituyendo en la ecuación de Bohr (ecuación \(\ref{6.3.3}\) para cada valor de energía, se obtiene:
\[ \Delta E=E_{final}-E_{initial}=-\dfrac{\Re hc}{n_{2}^{2}}-\left ( -\dfrac{\Re hc}{n_{1}^{2}} \right )=-\Re hc\left ( \dfrac{1}{n_{2}^{2}} - \dfrac{1}{n_{1}^{2}}\right ) \label{6.3.4}\]
Si n2 > n1, la transición es de un estado de mayor energía (u órbita más grande) a uno de menor energía (u órbita más pequeña), tal como muestra la flecha punteada en Figura \(\PageIndex{2}\) (a). Sustituyendo hc/λ para ΔE se obtiene:
\[ \Delta E = \dfrac{hc}{\lambda }=-\Re hc\left ( \dfrac{1}{n_{2}^{2}} - \dfrac{1}{n_{1}^{2}}\right ) \label{6.3.5}\]
Cancelando hc en ambos lados queda:
\[ \dfrac{1}{\lambda }=-\Re \left ( \dfrac{1}{n_{2}^{2}} - \dfrac{1}{n_{1}^{2}}\right ) \label{6.3.6}\]
Excepto por el signo negativo, la ecuación es igual a la obtenida por Rydberg experimentalmente. El signo en ecuación \(\ref{6.3.5}\) y \(\ref{6.3.6}\) indica que la energía es liberada al decaer un electrón de la órbita n2 a n1 porque la órbita n2 está a mayorenergía que n1. Bohr calculó \(\Re\) a partir de constantes fundamentales como la carga y la masa del electrón, y la constante de Planck. Encontró \(\Re\)=1.0974 × 107 m−1, el mismo valor que Rydberg obtuvo analizando el espectro de emisión del hidrógeno.
El modelo de Bohr permite comprender la física de las líneas de Balmer para el espectro de emisión del hidrógeno (Figura \(\PageIndex{3}\) b); las líneas corresponden a transiciones de órbitas con n > 2 a otra de n=2. La energía necesaria para la transición proviene de la descarga eléctrica, y la emisión, del decaimiento entre las órbitas nombradas (Figura \(\PageIndex{3}\) a). La transición de n = 3 a n = 2 origina la línea en 656 nm (rojo), de n = 4 a n = 2 en 486 nm (verde), de n = 5 a n = 2 en 434 nm (azul), y de n = 6 a n = 2 en 410 nm (violeta). La intensidad de las líneas de emisión depende del número de átomos en cada estado. A la temperatura del gas en el tubo hay más átomos en el nivel n = 3 que en n ≥ 4. En consecuencia, la transición de n = 3 a n = 2 es la más intensa, produciendo el color rojo característico del hidrógeno (Figura \(\PageIndex{1}\) a). Otra familia de líneas es producida por transiciones de n>1 a n=1 o a n≥3. Las transiciones previas se muestran esquemáticamente en la Figura \(\PageIndex{4}\).
Figura \(\PageIndex{4}\): Transiciones electrónicas que producen el espectro de emisión del hidrógeno. Las líneas de Lyman se deben a transiciones de estados excitados al estado basal (órbita con n=1); esas transiciones liberan gran energía, y corresponden a la region UV del espectro electromagnético. Las líneas de Paschen, Brackett, y Pfund se deben a transiciones de estados con alta energía a otros con n = 3, 4 y 5, respectivamente; tales transiciones liberan menos energía, y corresponden a radiación infrarroja del espectro. (El radio de las órbitas no está a escala.)
El tiempo de los átomos
Sistemas de telecomunicaciones, como los teléfonos celulares, dependen de señales que son precisas a nivel de la millonésima parte de segundo por día. Las señales del sistema de posicionamiento global (GPS, del inglés) deben ser precisas a nivel de la mil millonésima parte de segundo por día, que es equivalente sustraer o adicionar un segundo cada 1.400.000 años.
Alcanzar la precisión requerida actualmente ha tornado la atención de los físicos hacia el átomo, y en particular hacia las transiciones electrónicas. El estándar utilizado para calibrar relojes es el átomo de cesio. Átomos de cesio a elevada temperatura son colocados en una cámara de vacío y bombardeados con microondas, cuya frecuencia es cuidadosamente controlada. Cuando la energía coincide con una transición electrónica, se absorbe un fotón y el sistema se excita; además, el fenómeno ocurre a intervalos regulares, lo cual permite cuantificar el tiempo. Posteriormente, decae al estado de menor energía emitiendo radiación. La frecuencia de la microonda es cuidadosamente ajustada y sirve como péndulo del reloj.
En 1967, el segundo fue definido como la duración de 9.192.631.770 oscilaciones de la frecuencia resonante del átomo de cesio, llamado reloj de cesio. Investigaciones actuales buscan una nueva generación de relojes atómicos para ofrecer incluso una mayor precisión. Tales dispositivos permitirían a los neurocientíficos monitorear señales electromagnéticas muy débiles como las producidas en rutas nerviosas del cerebro y a los geólogos monitorear variaciones en los campos gravitacionales, que causan fluctuaciones en el tiempo, y ayudarían a descubrir minerales o petróleo.
Ejemplo \(\PageIndex{1}\): Las Líneas de Lyman
Las líneas de Lyman en el espectro de emisión del hidrógeno se deben a transiciones de estados electrónicos excitados al basal (n=1). a) Calcule la longitud de onda de la línea de Lyman de menor energía con tres cifras significativas. b) ¿En qué región del espectro electromagnético ocurre?
Dato: órbita de Lyman de menor energía.
Pregunta: longitud de la onda para la línea de Lyman de menor energía y región en el espectro
Estrategia:
A. Sustituir los valores apropiados en la ecuación 6.3.2 (ecuación de Rydberg) y encontrar λ.
B. Utilizar la Figura 2.2.1 para localizar la región del espectro electromagnético correspondiente a la onda calculada.
Solución:
A Puede utilizarse la ecuación de Rydberg para encontrar a longitud de onda:
\[ \dfrac{1}{\lambda }=-\Re \left ( \dfrac{1}{n_{2}^{2}} - \dfrac{1}{n_{1}^{2}}\right ) \]
Para las líneas de Lyman n1 = 1. La transición de menor energía es de n = 2 a n = 1, porque a mayor n mayor energía.
\[ \dfrac{1}{\lambda }=-\Re \left ( \dfrac{1}{n_{2}^{2}} - \dfrac{1}{n_{1}^{2}}\right )=1.097\times m^{-1}\left ( \dfrac{1}{1}-\dfrac{1}{4} \right )=8.228 \times 10^{6}\; m^{-1} \]
Los espectroscopistas (quienes estudian los espectros) utilizan cm-1 más que m-1 como unidad. El espectro electromagnético puede dividirse en esos términos. La región infrarroja barre aproximadamente el rango 200 - 5,000 cm-1, la visible 11,000 - 25,000 cm-1 y la UV 25,000 - 100,000 cm-1. La unidad de cm-1 se denomina número de onda, aunque suele verbalizarse como 'centímetros a la menos uno'. Puede convertirse el resultado previo a cm-1:
\[ \widetilde{\nu} =\dfrac{1}{\lambda }=8.228\times 10^{6}\cancel{m^{-1}}\left (\dfrac{\cancel{m}}{100\;cm} \right )=82,280\: cm^{-1} \]
y
\[\lambda = 1.215 \times 10^{−7}\; m = 122\; nm \]
Esta emisión de Lyman se denomina alfa. Es la emisión atómica más fuerte del sol y controla la química de la alta atmósfera en todos los planetas, produciendo iones al remover electrones de átomos y moléculas. Es completamente absorbida por el oxígeno en la alta estratósfera; disocia moléculas de O2 en átomos de O que pueden reaccionar con otras moléculas de O2 para formar el ozono estratosférico.
B Esta longitud de onda cae en la región ultravioleta del espectro.
Ejercicio \(\PageIndex{1}\): Líneas de Pfund
Las líneas de Pfund para el hidrógeno corresponden a transiciones de estados excitados a la capa n=5. Calcular la longitud de onda de la segunda línea de Pfund con tres cifras significativas. ¿En qué región del espectro cae?
Respuesta: 4.65 × 103 nm; infrarrojo.
El modelo de Bohr del átomo de hidrógeno da una explicación exacta del espectro de emisión observado. Sus contribuciones clave para el entendimiento de la estructura
atómica fueron:
- Los electrones pueden ocupar solo ciertas regiones del espacio, llamadas órbitas.
- Órbitas más cercanas al núcleo poseen menor energía.
- Los electrones pueden moverse de una órbita a otra absorbiendo o emitiendo energía, dando lugar al espectro característico del átomo.
Desafortunadamente, el modelo de Bohr no explica porqué un electrón está restringido a ciertas órbitas. Incluso tras ciertos ajustes tales como asumir órbitas elípticas en lugar de circulares, el modelo no pudo explicar cuantitativamente el espectro de emisión de elementos no hidrogenoides (Figura \(\PageIndex{5}\)). De hecho, el modelo de Bohr solo funciona para especies con un solo electrón (hidrogenoides): H, He+, Li2+, y demás. Se precisaría un cambio fundamental en el modo de pensar la estructura electrónica del átomo para ir más allá del modelo de Bohr.



Figura \(\PageIndex{5}\): Espectro de emisión de algunos elementos comparados con hidrógeno. (a) Hidrógeno molecular gaseoso, el cual es atomizado en el tubo de descarga; (b) Neón y (c) Mercurio. Las líneas más intensas en el espectro del hidrógeno ocurren en UV lejano (líneas de Lyman, comenzando en 124nm hacia abajo). Las líneas más fuertes del mercurio ocurren entre 181 y 254 nm, también en el UV. No se muestran.
Hasta aquí hemos considerado explícitamente solo la emisión de luz por átomos en estado excitado, que relajan a estados de menor energía produciendo el espectro de emisión. Inversamente, la absorción de luz de átomos en estado basal hacia un estado excitado produce un espectro de absorción. (espectro producido por la absorción de luz de átomos en estado basal). Cada elemento posee un espectro de emisión y absorción característico. Los científicos utilizan el fenómeno para estudiar la composición de la materia.
Al decaer a un estado de menor energía, el átomo emite luz; si absorbe luz, es excitado a un estado de mayor energía.
Estados de Energía del Átomo de Hidrógeno
Si un haz de luz blanca incide sobre una muestra con hidrógeno en estado basal, los átomos absorben energía al tiempo que un electrón pasa a nivel de mayor energía (órbitas con n ≥ 2). Si la luz emergente pasa por un prisma forma un espectro con regiones oscuras (longitudes de onda que no atraviesan de la muestra) en 656, 468, 434, and 410 nm. Esas longitudes de onda se dan por transiciones de n = 2 hacia n = 3, n = 4, n = 5 y n = 6 respectivamente. Todo elemento posee tanto un espectro de emisión como absorción característico, y son esencialmente imágenes complementarias.
Figura \(\PageIndex{6}\): A Interacción de luz con hidrógeno atómico. (a) Cuando el hidrógeno atómico absorbe un fotón de luz, un electrón es excitado hacia una órbita de mayor energía (capa o radio). (b) Espectro de emisión y absorción para hidrógeno.
Los espectros de emisión y absorción son la base de la espectroscopía, que los utiliza para extraer información sobre la composición de una sustancia o mezcla. En particular, los astrónomos utilizan espectros de emisión para determinar la composición de estrellas y materia interestelar. Como ejemplo, considere el espectro de luz solar de la Figura \(\PageIndex{7}\). Debido a que el sol está muy caliente, emite luz en un espectro continuo (radiación de cuerpo negro). Superpuesto con este, sin embargo, hay una serie de líneas oscuras consecuencia de la absorción de frecuencias específicas por átomos menos calientes, en la parte exterior de la atmósfera solar. Comparando estas líneas con el espectro de elementos medidos en la tierra, sabemos que el sol contiene enormes cantidades de hidrógeno, hierro, y carbono, como también cantidades menores de otros elementos. Durante el eclipse solar de 1868, el astrónomo francés Pierre Janssen (1824-1907) observó un conjunto de líneas que no coincidían con las de ningún elemento. En efecto, sugirió la presencia de un nuevo elemento, el cual nombró Helio, del griego helios que significa 'Sol'. El Helio fue finalmente descubierto en la Tierra en depósitos de uranio en 1895. Las partículas alfa son núcleos de helio emitidos por uranio radiactivo; atraen electrones de las rocas y forman átomos de helio.
Figura \(\PageIndex{7}\): Espectro visible de la luz solar. Las líneas oscuras características son principalmente debido a la absorción de luz por elementos de la capa externa de la atmósfera solar. Los elementos específicos se indican con etiquetas. Las líneas en 628 y 687 nm, sin embargo, se deben a la absorción de luz del oxígeno molecular en la atmósfera terrestre.
Veamos algunas transiciones electrónicas de elementos cotidianos. El conocido color rojo de carteles de publicidad es debido a transiciones electrónicas del neón, se muestra en parte (b) de la Figura \(\PageIndex{5}\). El amarillo o azul en luces de la calle se debe a descargas de mercurio o sodio, respectivamente. En todos los casos, una descarga eléctrica excita átomos neutros a un nivel de mayor energía, el átomo decae a un nivel de menor energía emitiendo radiación. En el caso del mercurio, la mayor parte de la emisión se da bajo 450 nm, lo cual produce luz azul (parte (c) en Figura \(\PageIndex{5}\)). En el sodio, la emisión más intensa es a 589 nm, produciendo luz amarilla.
Figura \(\PageIndex{8}\): Espectro de emisión de sodio y mercurio. Muchas luces de calle utilizan lámparas de sodio o mercurio gaseoso. Las líneas son ensanchadas por colisiones de los átomos. La línea oscura en el centro de la lámpara de sodio a elevada presión, donde la lámpara a baja presión es más fuerte, se debe a la absorción de luz en regiones más frías (externas) de la lámpara.
Resumen
Los átomos emiten radiación solo en longitudes de onda específicas, produciendo un espectro de líneas en lugar de un espectro continuo como el producido por objetos calientes. Niels Bohr explicó el espectro de líneas del hidrógeno asumiendo que el electrón se mueve en órbitas circulares y que las órbitas solo tienen cierta energía y cierto radio.
Las líneas en el espectro se explican por transiciones en las cuales un electrón se mueve de una órbita de cierto radio y energía a otra de diferente energía y radio. Órbitas más cercanas al núcleo o de menor radio poseen menor energía; las más lejanas poseen mayor energía. Las transiciones de estados excitados a otros de menor energía resulta en el espectro de emisión de luz de cierta longitud de onda. El proceso inverso origina el espectro de absorción. El modelo de Bohr, sin embargo, no explica el espectro de átomos con más de un electrón (no hidrogenoides).
Colaboradores
Modified by Joshua Halpern (Howard University)
Traducción de Santiago Miranda (Universidad Nacional de La Plata)

