6.5: Mecánica Cuántica y Orbitales Atómicos
- Page ID
- 2637
Objetivo
- Aplicar los resultados de la mecánica cuántica a la química.
El principio de incerteza de Heisenberg y la naturaleza ondulatoria de las partículas subatómicas imposibilitan utilizar la mecánica clásica para describir el movimiento de electrones en átomos. Los científicos necesitaron un nuevo acercamiento que tenga en cuenta el comportamiento ondulatorio del electrón. En 1926 el físico austríaco Erwin Schrödinger (1887-1961; Premio Nobel de Física 1933) desarrolló la mecánica ondulatoria, una técnica matemática que describe la relación entre el movimiento de partículas que exhiben propiedades ondulatorias (como el electrón) y sus energías permitidas.
Erwin Schrödinger (1887–1961)
La solución de Schrodinger no fue convencional, pero iba a la par de su modo de vida. Conocido era su desprecio a la memorización de datos y el aprendizaje de libros. Cuando Hitler asumió el poder en Alemania, Schrödinger escapó a Italia. Posteriormente trabajo en la Universidad de Princeton en los Estados Unidos pero eventualmente se trasladó al Instituto de Estudios Avanzados, Dublin, Irlanda, donde permaneció hasta su retiro en 1955.
Aunque la mecánica cuántica utiliza matemáticas sofisticadas, la descripción que se hace aquí es conceptual y no se precisarán detalles matemáticos para comprender las conclusiones generales. Se hará foco en las propiedades de las funciones de onda que son solución de la ecuación de Schrödinger.
Funciones de Onda
Una función de onda es una función matemática que relaciona la posición del electrón en un dado punto del espacio (identificado por x,y,z) a la amplitud de la onda, que corresponde a su energía. Entonces cada función de onda se asocia a un valor particular de energía E. Las propiedades de las funciones de onda derivadas de la mecánica cuántica se resumen a continuación.
- Una función de onda utiliza tres variables para describir la posición de un electrón (como las coordenadas cartesianas x,y,z). Además, una cuarta variable especifica el tiempo en el cual el objeto se encuentra en dicha posición. Por ejemplo, si se quiere interceptar un submarino enemigo, deberían conocerse latitud, longitud y altitud, como también el tiempo asociado a dicha posición (Figura 6.5.1). Para electrones podemos ignorar la dependencia temporal porque utilizaremos ondas estacionarias, las cuales por definición no varían en el tiempo.
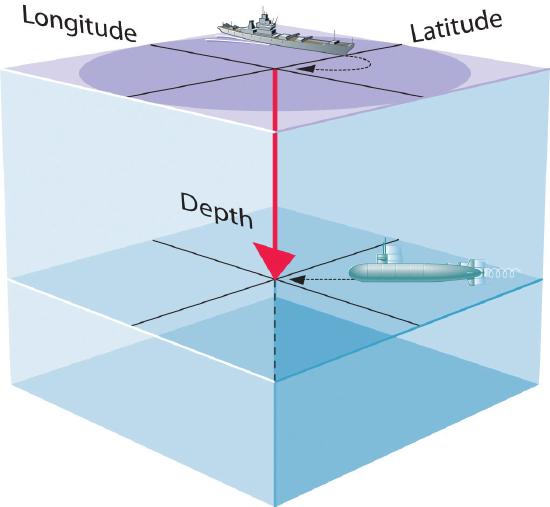
Figura \(\PageIndex{1}\): Las cuatro variables (Latitud, Longitud, Altitud y Tiempo) requeridas para localizar un objeto.</p>
- La magnitud de la función de onda en cierto punto del espacio es proporcional a la amplitud de la onda en ese punto. Muchas funciones de onda son funciones complejas, es decir, contienen el término matemático \(\sqrt{-1}\), representado como <em>i</em>. Entonces la amplitud de la onda no tiene significancia física real. En contraste, el signo de la función de onda (positivo o negativo) corresponde a la fase de la onda, que sera importante en nuestra discusion del enlace quimico. El signo de la función de onda no debe confundirse con un valor positivo o negativo de carga eléctrica.
- El cuadrado de la función de onda en un cierto punto es proporcional a la probabilidad de encontrar un electrón en ese punto del espacio, y origina una distribución de probabilidades en el espacio. El cuadrado de la función de onda (\(\Psi^2\)) es siempre una cantidad real [recall that that \(\sqrt{-1}^2=-1\)] y es proporcional a la probabilidad de encontrar un electrón en cierto punto. Más precisamente, la probabilidad está dada por el producto de la funcion Ψ y su complejo conjugado Ψ*, en el que todos los términos que contienen i son reemplazados por -i. Utilizamos probabilidades porque, de acuerdo al principio de incerteza de Heisenberg, no podemos precisar la posición un electrón. La probabilidad de encontrar un electrón en cierto punto del espacio es función de ciertos parámetros incluyendo la distancia al núcleo y, en muchos casos, el equivalente atómico de la longitud y latitud. La figura 6.5.2. muestra una manera de representar gráficamente la distribución de probabilidades -probabilidad de encontrar un electrón- para el estado basal del átomo de hidrógeno \(\PageIndex{2}\).
- Describir la distribución electrónica como una onda estacionaria origina conjuntos de números cuánticos que son característicos de cada función de onda. De los patrones mono y bidimencionales para ondas estacionarias mostrados previamente, esperarías (correctamente) que los patrones de ondas estacionarias tridimencionales fueran más complejos. Sin embargo, en el siglo 18 un matemático francés, Adrien Legendre (1752-1783), desarrollo un conjunto de ecuaciones describiendo el movimiento de ondas tidal en la superficie de un flooded planet. Schrödinger incorporó las ecuaciones de Legendre a sus funciones de onda. El requerimiento de que las ondas debieran estar en fase una con otra para evitar cancelarse y producir una onda estacionaria resulta en un número limitado de soluciones (funciones de onda), cada una especificada por un conjunto de números llamados números cuánticos.
- Cada función de onda esta asociada a un valor particular de energía. Como en el modelo de Bohr, la energía de un electrón en un átomo esta cuantizada; este puede acceder solo a ciertos valores de energía. La mayor diferencia entre el modelo de Bohr y el de Schrödinger es que el primero impone la idea de la cuantización arbitrariamente, mientras que en el de Schrödinger la cuantización es una consecuencia natural de la descripción del electrón como una onda estacionaria.
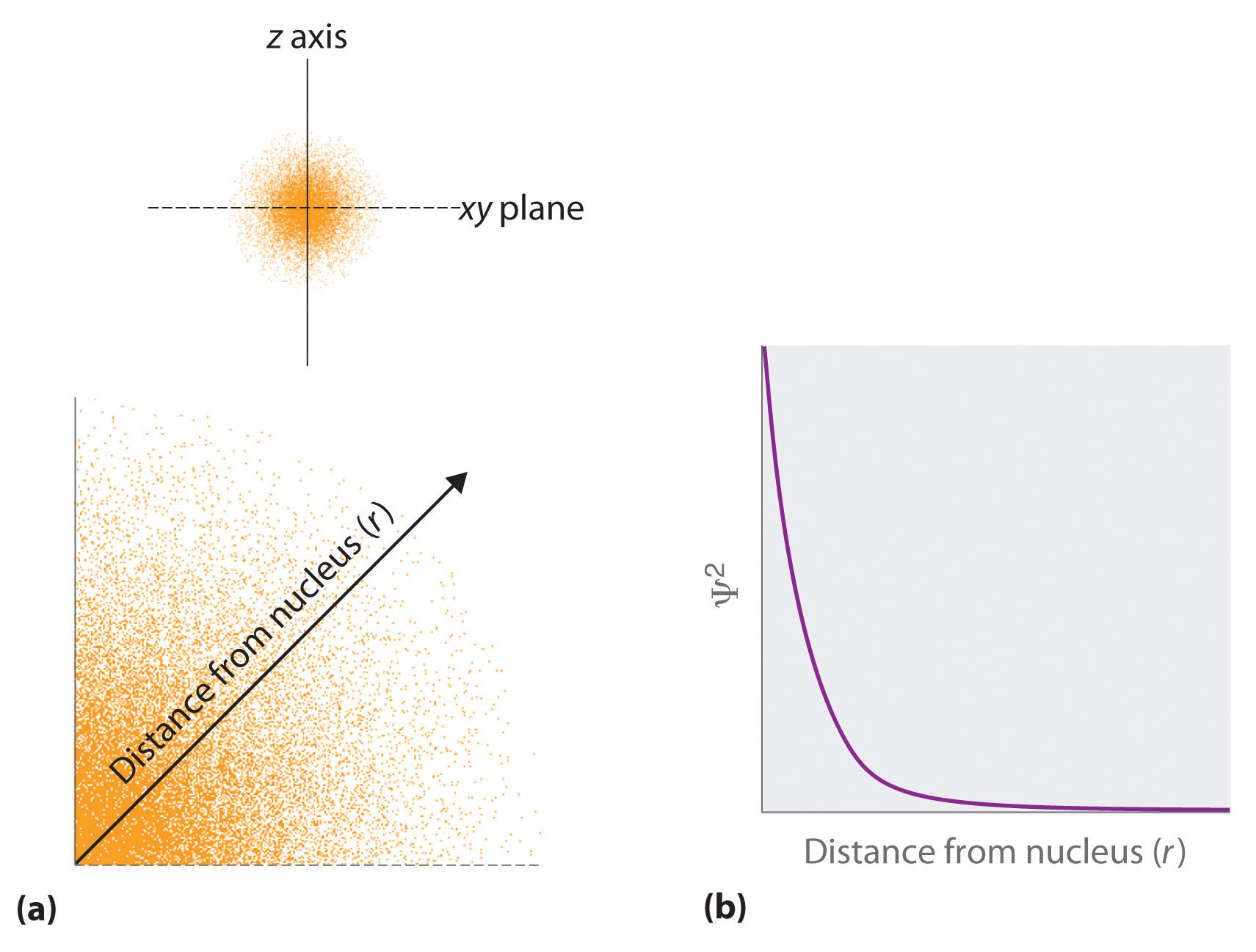
Figure \(\PageIndex{2}\): Probabilidad de Encontrar un Electrón en el Estado Basal del Átomo de Hidrógeno en diferentes puntos del espacio. (a) La densidad de los puntos refleja la probabilidad electrónica. (b) En este gráfico de Ψ2 vs r para el estado basal del átomo de hidrógeno, la densidad de probabilidad electrónica es mayor en r=0 (el núcleo) y decae al incrementar r. Debido a que la curva nunca alcanza el eje horizontal, la probabilidad de encontrar un electrón muy lejos del núcleo es pequeña pero no cero.
Números cuánticos
El acercamiento de Schrödinger utiliza tres números cuánticos (n, l y ml) para especificar cualquier función de onda. Los números cuánticos proveen información sobre la distribución espacial del electrón. Aunque n puede ser cualquier entero positivo, solo ciertos valores de l y ml están permitidos para un cierto valor de n.
Número Cuántico Principal
El número cuántico principal (n) refleja la distancia promedio entre un electrón y el núcleo:
\[n = 1, 2, 3, 4,… \label{6.5.1}\]
A medida que n incrementa para un dado átomo, así lo hace la distancia promedio de un electrón al núcleo. Un electrón negativamente cargado que, en promedio, se encuentra más cerca del núcleo atómico (positivamente cargado) es atraído mas fuertemente que un electrón mas lejos. Esto implica que electrones con valores grandes de n serán más fácilmente removidos del átomo. Todas las funciones de onda que poseen mismo n se dice que constituyen la capa principal porque esos electrones tendrán similares distancias promedio al núcleo. Como veras el numero cuántico principal n corresponde al utilizado por Bohr para describir las órbitas electrónicas y por Rydberg para describir los niveles de energía atómicos.
Número Cuántico Azimutal
El segundo número cuántico es frecuentemente denominado número cuántico azimutal (l). El valor de l describe la forma de la región del espacio ocupada por el electrón. Los valores permitidos de l dependen del valor de n y van de 0 a n-1:
\[l = 0, 1, 2,…, n − 1 \label{6.5.2}\]
Por ejemplo, si n=1, l can be 0: if n=2, l can be 0 or 1; y así siguiendo. Para un dado átomo, todas las funciones de onda que tienen los mismos valores de n y l forman una subcapa. Las regiones del espacio ocupadas por electrones en la misma subcapa usualmente tienen la misma forma, pero están orientadas de manera diferente en el espacio.
Número Cuántico Magnético
El tercer número cuántico es el número cuántico magnético (\(m_l\)). El valor de \(m_l\) describe la orientación de la region del espacio ocupada por un electrón respecto a un campo mangético aplicado. Los valores de \(m_l\) depende del valor de l: ml varía desde 'l a l en valores enteros.
\[m_l = −l, −l + 1,…, 0,…, l − 1, l \label{6.5.3}\]
Por ejemplo si \(l = 0\), \(m_l\) solo puede ser 0; si l = 1, ml puede ser −1, 0, or +1; y si l = 2, ml puede ser −2, −1, 0, +1, or +2.
Cada función de onda posee una combinación de n, l, y ml que describe al orbital, una distribución espacial del electrón. Para un conjunto de números cuánticos, cada capa principal tiene un número fijo de subcapas, y cada subcapa tiene un numero definido de orbitales.
Ejemplo \(\PageIndex{1}\): Estructura de la capa n=4
Cuantas subcapas y orbitales contiene la capa con n=4?
Dato: valor de n
Se pide: número de subcapas y orbitales en la capa principal.
Estrategia:
Dado n=4, calcular los valores permitidos de l. De estos valores permitidos, se deduce el número de subcapas. Para cada valor de l,
calcular los valores de ml. La suma del número de orbitales en cada subcapa es el número de orbitales en la capa principal.
Solución:
A. l toma valores enteros entre 0 y n-1, entonces puede ser 0, 1, 2, o 3. Debido a que la capa tiene cuatro valores de l, tiene cuatro subcapas, cada una de las cuales contendrá un número diferente de orbitales, dependiendo de los valores permitidos de ml.
B. Para l=0, ml debe ser 0, entonces la subcapa l=0 tiene solo un orbital. Para l=1, ml puede ser 0, 1 y -1. Entonces l=1 posee tres orbitales, para el cual ml puede ser 0, 1, 2, 3, -1, -2, -3, resultando en siete orbitales en la subcapa con l=3. El número total de orbitales en la capa n=4 es la suma de los orbitales en cada subcapa y es igual a n2 = 16
Ejercicio \(\PageIndex{1}\) Estructura de la capa n=3
Cuántas subcapas y orbitales contiene la capa principal con n = 3?
- Respuesta
-
Tres subcapas, nueve orbitales.
Más que especificar todos los valores de n y l cada vez que se refiere a una subcapa o un orbital, los químicos utilizan una abreviación en letras minúsculas para denotar el valor de l para una subcapa u orbital particular:
| l | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Designación | s | p | d | f |
El número cuántico principal es nombrado primero, seguido de las letras s, p, d, f dependiendo el caso. Tales designaciones son derivadas de características espectroscópicas: sharp (agudo), principle (principal), diffuse (difuso) y fundamental. Un orbital 1s posee n = 1 y l = 0; la subcapa 2p tiene n = 2 y l = 1 (y tiene tres orbitales 2p, correspondiente a ml = −1, 0, and +1); la subcapa 3d posee n = 3 y l = 2 (y posee cinco orbitales 3d, correspondientes a ml = −2, −1, 0, +1, y +2); y así siguiendo.
Podemos resumir las relaciones entre los números cuánticos y el número de subcapas y orbitales como sigue (Tabla 6.5.1)
- Cada capa principal tiene n subcapas. Para n = 1, una sola subcapa es posible (1s); para n = 2, hay dos subcapas (2s y 2p); para n = 3, hay tres subcapas (3s, 3p, y 3d); y así siguiendo. Cada capa tiene ns subcapas, cualquier capa con n ≥ 2 también tiene una subcapa np, y cualquier capa con n ≥ 3 también tiene una subcapa nd. Debido a que una subcapa 2d requería ambas n = 2 y l = 2, el cual no es un valor permitido de l para n = 2, la subcapa 2d no existe.
- Cada subcapa tiene 2l + 1 orbitales. Esto significa que todas las subcapas ns contienen un único orbital s, todas las subcapas np contienen tres orbitales p, todas las subcapas nd contienen 5 orbitales d, y todas las subcapas nf contienen siete orbitales f.
Cada capa principal tiene n subcapas y cada subcapa 2l + 1 orbitales.
| n | l | Subshell Designation | \(m_l\) | Number of Orbitals in Subshell | Number of Orbitals in Shell |
|---|---|---|---|---|---|
| 1 | 0 | 1s | 0 | 1 | 1 |
| 2 | 0 | 2s | 0 | 1 | 4 |
| 1 | 2p | −1, 0, 1 | 3 | ||
| 3 | 0 | 3s | 0 | 1 | 9 |
| 1 | 3p | −1, 0, 1 | 3 | ||
| 2 | 3d | −2, −1, 0, 1, 2 | 5 | ||
| 4 | 0 | 4s | 0 | 1 | 16 |
| 1 | 4p | −1, 0, 1 | 3 | ||
| 2 | 4d | −2, −1, 0, 1, 2 | 5 | ||
| 3 | 4f | −3, −2, −1, 0, 1, 2, 3 | 7 |
Resumen
El movimiento de electrones en átomos y moléculas y su energía es descripto por la mecánica cuántica. Debido a la dualidad onda-partícula, los científicos deben lidiar con la probabilidad de un electrón en cierto punto del espacio.Esto requirió el desarrollo de la mecánica cuántica, que utiliza las funciones de onda (Ψ) para describir la relación matemática entre el movimiento de los electrones en átomos y moléculas con sus energías. Las funciones de onda tienen propiedades importantes:
- La función de onda utiliza tres variables (ejes cartesianos x,y,z) para describir la posición de un electrón;
- La magnitud de la función de onda es proporcional a la intensidad de la onda;
- La probabilidad de encontrar un electrón en un cierto punto del espacio es proporcional al cuadrado de la función de onda en ese punto, produciendo una distribución de probabilidades en el espacio que es usualmente representada en un gráfico de densidad electrónica.
- La descripción de distribuciones electrónicas como ondas estacionarias lleva naturalmente a la existencia un conjunto de números característicos de cara función de onda, denominados números cuánticos.
- Cada distribución espacial del electrón es descripta por una función de onda con un dado conjunto de números cuánticos y una energía particular.
Los números cuánticos proveen información importante sobre la energía y la distribución espacial de un electrón. El número cuántico principal n puede ser cualquier entero positivo; al incrementar n para un átomo, la distancia promedio de un electrón al núcleo también incrementa. Todas las funciones de onda de un mismo valor de n constituyen la capa principal en la cual los electrones tienen similar distancia promedio al núcleo. El número cuántico azimutal l puede tener valores enteros entre 0 y n-1; describe la forma de la distribución electrónica. Funciones de onda que tienen iguales valores de n y l constituyen una subcapa, correspondiendo a las distribuciones electrónicas que usualmente difieren en la orientación más que en la forma o la distancia promedio al núcleo. El número cuántico magnético ml posee 2l+1 valores, variando entre -l y l, y describe la orientación de la distribución electrónica. Cada función de onda con un dado set de valores n,l y ml describe una distribución espacial particular del electrón en un átomo, un orbital atómico.
Colaboradores
Traducción de Santiago Miranda (Universidad Nacional de La Plata)

