2.3: La estructura atómica y el simbolismo

Última actualización
Guardar como PDF

Page ID: 1804

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Habilidades para desarrollar

Escribir y también interpretar los símbolos que representan el número atómico, el número de masa y la carga de un átomo o ion.
Definir la unidad de masa atómica y la masa atómica promedio.
Calcular la masa atómica promedio y la abundancia isotópica.

El desarrollo de la teoría atómica moderna reveló mucho sobre la estructura interna de los átomos. Se aprendió que un átomo contiene un núcleo muy pequeño compuesto de protones con carga positiva y neutrones sin carga, rodeados por un volumen mucho más grande de espacio que contiene electrones con carga negativa. El núcleo contiene la mayoría de la masa de un átomo porque los protones y los neutrones son mucho más pesados que los electrones, mientras que los electrones ocupan casi todo el volumen de un átomo. El diámetro de un átomo es del orden de 10^-10 m, mientras que el diámetro del núcleo es aproximadamente 10^-¹⁵m, aproximadamente 100,000 veces más pequeño. Para una perspectiva sobre sus tamaños relativos, considere esto: si el núcleo fuera del tamaño de un arándano, el átomo sería del tamaño de un estadio de fútbol (Figura \(\PageIndex{1}\)).

The diagram on the left shows a picture of an atom that is 10 to the negative tenth power meters in diameter. The nucleus is labeled at the center of the atom and is 10 to the negative fifteenth power meters. The central figure shows a photograph of an American football stadium. The figure on the right shows a photograph of a person with a handful of blueberries. — Figura \(\PageIndex{1}\): Si un átomo se pudiera expandir al tamaño de un estadio de fútbol, el núcleo sería el tamaño de un solo arándano. (Crédito medio: modificación del trabajo por "babyknight"/Wikimedia Commons; derecho de crédito: modificación del trabajo por Paxson Woelber).

Los átomos, y los protones, neutrones, y electrones que los componen son muy pequeños. Por ejemplo, un átomo de carbono pesa menos de 2 \(\times\) 10 ^-23 g, y un electrón tiene una carga de menos de 2 \(\times\) 10 ^-19 C (coulomb). Cuando describimos las propiedades de objetos pequeños como los átomos, usamos unidades de medida apropiadamente pequeñas, como la unidad de masa atómica (amu) y la unidad fundamental de carga (e). La unidad de amu se definió originalmente basado al hidrógeno, el elemento más liviano, y luego fue definido en términos de oxígeno. Desde 1961, se ha definido con respecto al isótopo de carbono más abundante, a los cuales se les asignan masas de exactamente 12 amu. (Este isótopo se conoce como "carbono 12", como se explicará más adelante en este módulo). Por lo tanto, un amu es exactamente \(1/12\) de la masa de un átomo de carbono 12: 1 amu = 1,6605 \(\times\) 10 ^-24 g. (El Dalton (Da) y la unidad de masa atómica unificada (u) son unidades alternativas que son equivalentes a la amu.) La unidad de carga fundamental (también llamada carga elemental) es igual a la magnitud de la carga de un electrón (e) con e = 1,602 \(\times\) 10⁻¹⁹ C.

Un protón tiene una masa de 1,0073 amu y una carga de 1+. Un neutrón es una partícula un poco más pesada con una masa de 1.0087 amu y una carga de cero; como su nombre lo indica, es neutral. El electrón tiene una carga de 1− y es una partícula mucho más ligera con una masa de aproximadamente 0,00055 amu (se necesitan alrededor de 1800 electrones para igualar la masa de un protón. Las propiedades de estas partículas fundamentales se resumen en la Tabla \(\PageIndex{1}\). (Un estudiante observando podría notar que la suma de las partículas subatómicas de un átomo no es igual a la masa real del átomo: la masa total de seis protones, seis neutrones y seis electrones es 12,0993 amu, un poco más que los 12.00 amu de un átomo de carbono 12. Esta masa "faltante" se conoce como el defecto de masa, y usted aprenderá sobre esto en el capítulo de química nuclear.

Tabla \(\PageIndex{1}\): Propiedades de las Partículas Subatómicas
Nombre	Locación	Carga (C)	Carga de Unidad	Masa (amu)	Masa (g)
electrón	fuera del núcleo	\(−1.602 \times 10^{−19}\)	1−	0.00055	\(0.00091 \times 10^{−24}\)
proton	núcleo	\(1.602 \times 10^{−19}\)	1+	1.00727	\(1.67262 \times 10^{−24}\)
neutrón	núcleo	0	0	1.00866	\(1.67493 \times10^{−24}\)

El número de protones en el núcleo de un átomo es su número atómico (Z). Este es el atributo definitorio de un elemento: su valor determina la identidad del átomo. Por ejemplo, cualquier átomo que contiene seis protones es el elemento carbono y tiene el número atómico 6, independientemente de cuántos neutrones o electrones pueda tener. Un átomo neutro debe contener el mismo número de cargas positivas y negativas; el número de protones es igual al número de electrones. Por lo tanto, el número atómico también indica el número de electrones en un átomo. El número total de protones y neutrones en un átomo se llama el número de masa (A). El número de neutrones es la diferencia entre el número de masa y el número atómico: A - Z = número de neutrones.

\[\begin{align*}
\ce{atomic\: number\:(Z)\: &= \:number\: of\: protons\\
mass\: number\:(A)\: &= \:number\: of\: protons + number\: of\: neutrons\\
A-Z\: &= \:number\: of\: neutrons}
\end{align*}\]

Los átomos son eléctricamente neutros si tienen la misma cantidad de protones cargados positivamente y electrones que están cargados negativamente. Cuando los números de estas partículas subatómicas no son iguales, el átomo está cargado eléctricamente y se llama un ión. La carga de un átomo se define en la siguiente manera:

Carga Atómica = número de protones - número de electrones

Como se explicará con más detalle más adelante en este capítulo, los átomos (y las moléculas) generalmente adquieren carga al ganar o perder electrones. Un átomo que gana uno o más electrones exhibirá una carga negativa y se llamará un anión. Los átomos con carga positiva llamados cationes se forman cuando un átomo pierde uno o más electrones. Por ejemplo, un átomo neutro de sodio (Z = 11) tiene 11 electrones. Si este átomo pierde un electrón, se convertirá en un catión con una carga de 1+ (11 - 10 = 1+). Un átomo neutro de oxígeno (Z = 8) tiene ocho electrones, y si gana dos electrones se convertirá en un anión con una carga de 2- (8 − 10 = 2−).

Ejemplo \(\PageIndex{1}\): Composición de un Átomo

El yodo es un elemento de traza que es esencial en nuestra dieta; se necesita para producir la hormona tiroidea. La falta de yodo en la dieta puede llevar al desarrollo de un bocio, un agrandamiento de la glándula tiroides. (Figura \(\PageIndex{2}\)).

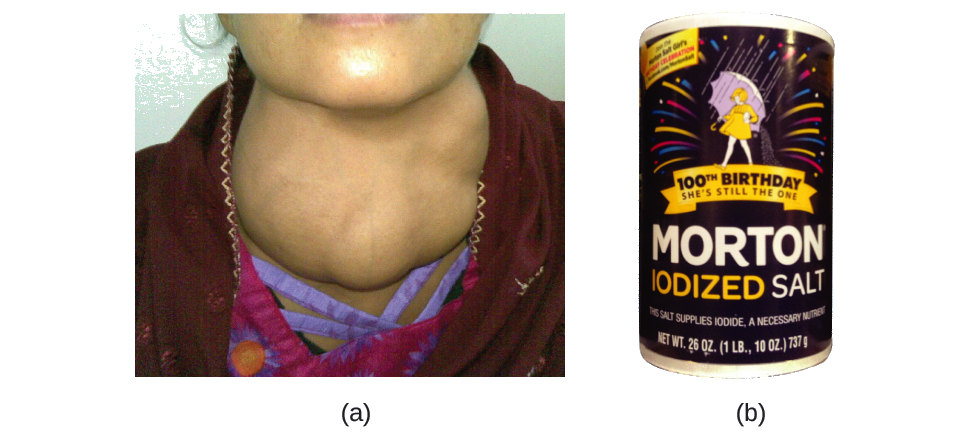
Figure A shows a photo of a person who has a very swollen thyroid in his or her neck. Figure B shows a photo of a canister of iodized salt. — Figura \(\PageIndex{2}\):(a) La falta de yodo en la dieta puede causar un agrandamiento de la glándula tiroides llamado bocio. (b) La adición de pequeñas cantidades de yodo a la sal, que previene la formación de bocios, ha ayudado a eliminar esta preocupación en los EE.UU., donde el consumo de la sal es alto. (Crédito a: modificación del trabajo por "Almazi"/Wikimedia Commons; crédito b: modificación del trabajo por Mike Mozart)

La adición de pequeñas cantidades de yodo a la sal de mesa (sal yodada) esencialmente ha eliminado este problema de salud en los Estados Unidos, pero hasta el 40% de la población mundial todavía está en riesgo de deficiencia del yodo. Los átomos de yodo se agregan como aniones, y cada uno tiene una carga 1- y una masa de 127. Determine el número de protones, neutrones y electrones en uno de estos aniones de yodo.

Solución

El número atómico del yodo (53) nos dice que un átomo neutro de yodo contiene 53 protones en su núcleo y 53 electrones afuera de su núcleo. Dado que la suma de los números de protones y neutrones es igual al número de masa, 127, el número de neutrones es 74 (127 - 53 = 74). Dado que el yodo se agrega como un anión 1−, el número de electrones es 54 [53 - (1–) = 54].

Ejercicio \(\PageIndex{1}\)

Un ion de platino tiene una masa de 195 y contiene 74 electrones. ¿Cuántos protones y neutrones contiene, y cuál es su carga?

Respuesta: 78 protones; 117 neutrones; la carga es 4+

Los símbolos químicos

Un símbolo químico es una abreviatura que usamos para indicar un elemento o un átomo de un elemento. Por ejemplo, el símbolo para el mercurio es Hg (Figura \(\PageIndex{3}\)). Usamos el mismo símbolo para indicar un átomo de mercurio (dominio microscópico) o para etiquetar un contenedor de muchos átomos del elemento mercurio (dominio macroscópico).

A jar is shown with a small amount of liquid mercury in it. — Figura \(\PageIndex{3}\): El símbolo Hg representa el elemento mercurio sin importar la cantidad; podría representar un átomo de mercurio o una gran cantidad de mercurio. Imagen utilizada con permiso de Wikipedia (user: Materialscientist).

Los símbolos de varios elementos comunes y sus átomos se listan en la Tabla \(\PageIndex{2}\). Algunos símbolos se derivan del nombre común del elemento; otros son abreviaturas del nombre en otro idioma. Los símbolos tienen una o dos letras, por ejemplo, H para hidrógeno y Cl para cloro. Para evitar confusiones con otras notaciones, solo se escribe con mayúscula la primera letra de un símbolo. Por ejemplo, Co es el símbolo para el elemento cobalto, pero CO es la notación para el compuesto monóxido de carbono, que contiene átomos de los elementos carbono (C) y oxígeno (O). Todos los elementos conocidos y sus símbolos están en la tabla periódica

Tabla \(\PageIndex{2}\): Algunos Elementos Comunes y sus Símbolos
Elemento	Símbolo	Elemento	Símbolo
aluminio	Al	hierro	Fe (de ferrum)
bromo	Br	plomo	Pb (de plumbum)
calcio	Ca	magnesio	Mg
carbón	C	mercurio	Hg (de hydrargyrum)
cloro	Cl	nitrógeno	N
cromo	Cr	oxígeno	O
cobalto	Co	potasio	K (de kalium)
cobre	Cu (from cuprum)	silicio	Si
flúor	F	plata	Ag (de argentum)
oro	Au (from aurum)	sodio	Na (de natrium)
helio	He	azufre	S
hidrógeno	H	estaño	Sn (de stannum)
yodo	I	estaño	Zn

Tradicionalmente, el descubridor (o descubridores) de un nuevo elemento nombran el elemento. Sin embargo, hasta que el nombre sea reconocido por la Unión Internacional de Química Pura y Aplicada (IUPAC), el nombre recomendado para el nuevo elemento se basa en la(s) palabra(s) latina(s) para su número atómico. Por ejemplo, el elemento 106 fue llamado unnilhexium (Unh), el elemento 107 fue llamado unnilseptium (Uns), y el elemento 108 fue llamado unniloctium (Uno) por varios años. Estos elementos ahora llevan el nombre de científicos o lugares; por ejemplo, el elemento 106 ahora se conoce como seaborgium (Sg) en honor de Glenn Seaborg, un ganador del Premio Nobel que participó activamente en el descubrimiento de varios elementos pesados.

Los isótopos

El símbolo para un isótopo específico de cualquier elemento se escribe colocando el número de masa como un superíndice a la izquierda del símbolo del elemento (Figura \(\PageIndex{4}\)). A veces, el número atómico se escribe como un subíndice que precede al símbolo, pero como este número define la identidad del elemento, al igual que su símbolo, se omite a veces. Por ejemplo, el magnesio existe como una mezcla de tres isótopos, cada uno con un número atómico de 12 y con números de masa de 24, 25 y 26, respectivamente. Estos isótopos pueden ser identificados como ²⁴Mg, ²⁵Mg, and ²⁶Mg. Estos símbolos de isótopos se leen como "elemento, número de masa" y se pueden simbolizar de manera consistente con esta lectura. Por ejemplo, ²⁴Mg se lee como “magnesio 24,” y se puede escribir como “magnesio-24” o “Mg-24.” ²⁵Mg se lee como “magnesio 25,” y se puede escribir como “magnesio-25” o “Mg-25.” Estos símbolos de isótopos se leen como "elemento, número de masa" y se pueden simbolizar de manera consistente con esta lectura. Por ejemplo,el átomo de ²⁴Mg tiene 12 neutrones en su núcleo, un ²⁵Mg atom tiene 13 neutrones, y ²⁶Mg tiene 14 neutrones.

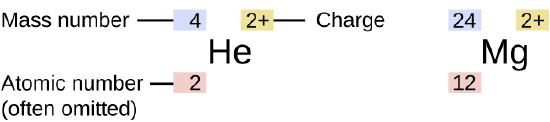
This diagram shows the symbol for helium, “H e.” The number to the upper left of the symbol is the mass number, which is 4. The number to the upper right of the symbol is the charge which is positive 2. The number to the lower left of the symbol is the atomic number, which is 2. This number is often omitted. Also shown is “M g” which stands for magnesium It has a mass number of 24, a charge of positive 2, and an atomic number of 12. — Figura \(\PageIndex{4}\): El símbolo para un átomo indica el elemento a través de su símbolo de dos letras, el número de masa como un superíndice izquierdo, el número atómico como un subíndice izquierdo (a veces se omite) y la carga como un superíndice derecho.

La información sobre los isótopos naturales de los elementos con números atómicos del 1 al 10 se dan en la Tabla \(\PageIndex{2}\). Tenga en cuenta que, además de los nombres y símbolos estándar, a veces se hace referencia a los isótopos del hidrógeno usando nombres comunes y símbolos que los acompañan. El hidrógeno -2, simbolizado en ²H, también se llama deuterio y, a veces, se simboliza como D. El hidrógeno-3, se simboliza en ³H, también se llama tritio y en ocasiones, se simboliza con T.

Table \(\PageIndex{2}\): Nuclear Compositions of Atoms of the Very Light Elements
Elemento	Símbolo	Número Atómico	Número de Protones	Número de Neutrones	Masa (amu)	% Abundancia Natural
hidrógeno	\(\ce{^1_1H}\) (protium)	1	1	0	1.0078	99.989
	\(\ce{^2_1H}\) (deuterium)	1	1	1	2.0141	0.0115
	\(\ce{^3_1H}\) (tritium)	1	1	2	3.01605	— (trace)
helio	\(\ce{^3_2He}\)	2	2	1	3.01603	0.00013
helio	\(\ce{^4_2He}\)	2	2	2	4.0026	100
litio	\(\ce{^6_3Li}\)	3	3	3	6.0151	7.59
litio	\(\ce{^7_3Li}\)	3	3	4	7.0160	92.41
berilio	\(\ce{^9_4Be}\)	4	4	5	9.0122	100
boro	\(\ce{^{10}_5B}\)	5	5	5	10.0129	19.9
boro	\(\ce{^{11}_5B}\)	5	5	6	11.0093	80.1
carbón	\(\ce{^{12}_6C}\)	6	6	6	12.0000	98.89
	\(\ce{^{13}_6C}\)	6	6	7	13.0034	1.11
	\(\ce{^{14}_6C}\)	6	6	8	14.0032	— (trace)
nitrógeno	\(\ce{^{14}_7N}\)	7	7	7	14.0031	99.63
nitrógeno	\(\ce{^{15}_7N}\)	7	7	8	15.0001	0.37
oxígeno	\(\ce{^{16}_8O}\)	8	8	8	15.9949	99.757
	\(\ce{^{17}_8O}\)	8	8	9	16.9991	0.038
	\(\ce{^{18}_8O}\)	8	8	10	17.9992	0.205
flúor	\(\ce{^{19}_9F}\)	9	9	10	18.9984	100
neón	\(\ce{^{20}_{10}Ne}\)	10	10	10	19.9924	90.48
	\(\ce{^{21}_{10}Ne}\)	10	10	11	20.9938	0.27
	\(\ce{^{22}_{10}Ne}\)	10	10	12	21.9914	9.25

La masa atómica

Porque cada protón y cada neutrón contribuyen aproximadamente un amu a la masa de un átomo, y cada electrón contribuye mucho menos, la masa atómica de un solo átomo es aproximadamente igual a su número de masa (un número entero). Sin embargo, las masas promedio de los átomos de la mayoría de los elementos no son números enteros porque la mayoría de los elementos existen naturalmente como mezclas de dos o más isótopos.

La masa de un elemento que se muestra en una tabla periódica o que esté listado en una tabla de masas atómicas es una masa promedio de todos los isótopos presentes en una muestra natural de ese elemento. Esto es igual a la suma de la masa de cada isótopo individual multiplicada por su abundancia fraccional.

\[\mathrm{average\: mass}=\sum_{i}(\mathrm{fractional\: abundance\times isotopic\: mass})_i\]

Por ejemplo, el elemento boro está compuesto de dos isótopos: aproximadamente el 19,9% de todos los átomos de boro son ¹⁰B con una masa de 10,0129 amu, y el 80,1% restante son ¹¹B con una masa de 11,0093 amu. La masa atómica promedio para el boro se calcula a ser:

\[\begin{align*}
\textrm{boron average mass} &=\mathrm{(0.199\times10.0129\: amu)+(0.801\times11.0093\: amu)}\\
&=\mathrm{1.99\: amu+8.82\: amu}\\
&=\mathrm{10.81\: amu}
\end{align*}\]

Es importante entender que ningún átomo de boro pesa exactamente 10,8 amu; 10,8 amu es la masa promedio de todos los átomos de boro, y los átomos de boro individuales pesan aproximadamente 10 amu o 11 amu.

Ejemplo \(\PageIndex{2}\): CALCULACIÓN DE LA MASA ATÓMICA promedio

Un meteorito encontrado en el centro de Indiana contiene rastros del gas noble neón, recogido del viento solar durante el viaje del meteorito a través del sistema solar. El análisis de una muestra del gas mostró que consistía en 91,84% ²⁰Ne (masa 19,9924 amu), 0,47% ²¹Ne (masa 20,9940 amu), y 7,69% ²²Ne (masa 21,9914 amu). ¿Cuál es la masa promedio del neón en el viento solar?

Solución

\[\begin{align*}
\mathrm{average\: mass} &=\mathrm{(0.9184\times19.9924\: amu)+(0.0047\times20.9940\: amu)+(0.0769\times21.9914\: amu)}\\
&=\mathrm{(18.36+0.099+1.69)\:amu}\\
&=\mathrm{20.15\: amu}
\end{align*}\]

La masa promedio de un átomo de neón en el viento solar es de 20,15 amu. (La masa promedio de un átomo de neón terrestre es 20,1796 amu. Este resultado demuestra que podemos encontrar pequeñas diferencias en la abundancia natural de isótopos, dependiendo de su origen)

Ejercicio \(\PageIndex{2}\)

Se encuentra una muestra de magnesio que contiene 78,70% de ²⁴Mg átomo (masa 23,98 amu), 10,13% de ²⁵Mg átomos (masa 24,99 amu), y 11,17% de ²⁶Mg átomo (masa 25,98 amu).Calcule la masa promedio de un átomo de Mg.

Respuesta: 24,31 amu

También podemos hacer variaciones de este tipo de cálculo, como se muestra en el siguiente ejemplo.

Ejemplo \(\PageIndex{3}\): CÁLCULO DEl porcentaje de la abundancia

El cloro natural está compuesto de ³⁵Cl (masa 34,96885 amu) y ³⁷Cl (masa 36,96590 amu), con una masa promedio de 35,453 amu. ¿Cuál es el porcentaje de composición de Cl en términos de estos dos isótopos?

Solución

La masa promedio de cloro es la fracción que es ³⁵Cl multiplicado por la masa de ³⁵Cl más la fracción que es ³⁷Cl multiplicado por la masa de ³⁷Cl.

\[\mathrm{average\: mass=(fraction\: of\: ^{35}Cl\times mass\: of\: ^{35}Cl)+(fraction\: of\: ^{37}Cl\times mass\: of\: ^{37}Cl)}\]

Si dejamos que x represente la fracción que es ³⁵Cl, entonces la fracción que es ³⁷Cl está representado por 1.00 − x.

(La fracción que es ³⁵Cl + la fracción que es ³⁷Cl debe sumar hasta 1, para que la fracción de ³⁷Cl debe ser igual a 1.00 − la fracción de ³⁵Cl.)

Sustituyendo esto en la ecuación de masa promedio, tenemos:

\[\begin{align*}
\mathrm{35.453\: amu} &=(x\times 34.96885\: \ce{amu})+[(1.00-x)\times 36.96590\: \ce{amu}]\\
35.453 &=34.96885x+36.96590-36.96590x\\
1.99705x &=1.513\\
x&=\dfrac{1.513}{1.99705}=0.7576
\end{align*}\]

Entonces, resolviendo los rendimientos: x = 0.7576, lo que significa que 1.00 - 0.7576 = 0.2424. Por lo tanto, el cloro consiste en 75,76% ³⁵Cl y 24,24% ³⁷Cl.

Ejercicio \(\PageIndex{3}\)

El cobre natural se compone de ⁶³Cu (masa 62,9296 amu) y ⁶⁵Cu (masa 64,9278 amu), con una masa promedio de 63,546 amu. ¿Cuál es el porcentaje de composición de Cu en términos de estos dos isótopos?

Respuesta: 69,15% Cu-63 y 30,85% Cu-65

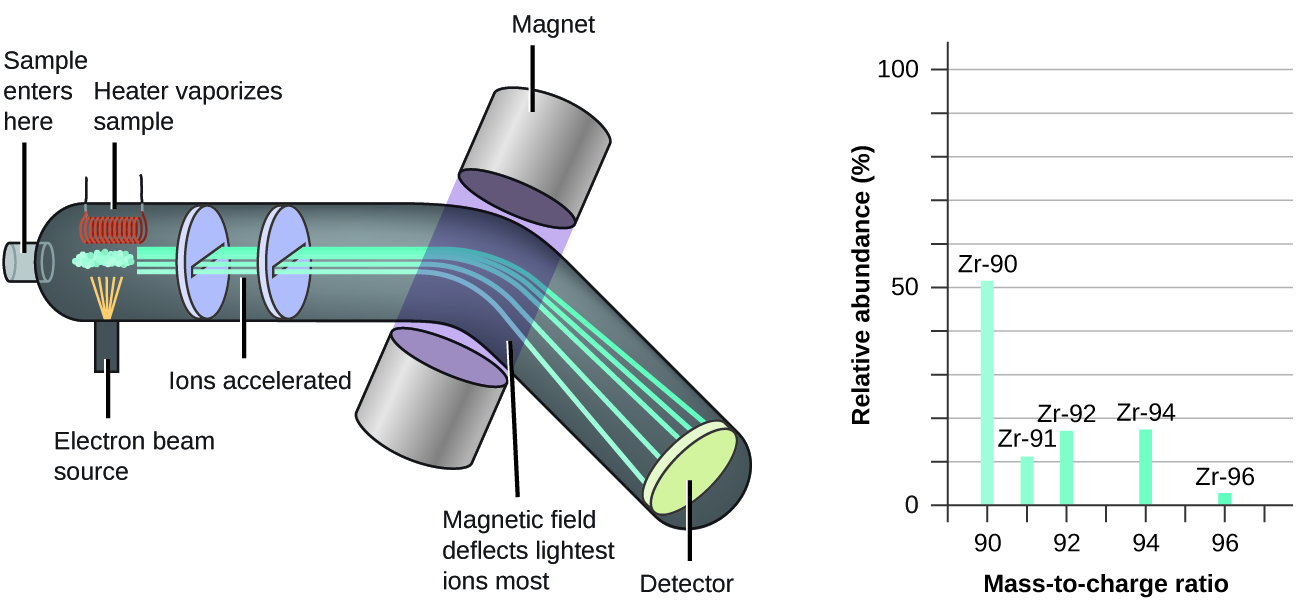
The left diagram shows how a mass spectrometer works, which is primarily a large tube that bends downward at its midpoint. The sample enters on the left side of the tube. A heater heats the sample, causing it to vaporize. The sample is also hit with a beam of electrons as it is being vaporized. Charged particles from the sample, called ions, are then accelerated and pass between two magnets. The magnetic field deflects the lightest ions most. The deflection of the ions is measured by a detector located on the right side of the tube. The graph to the right of the spectrometer shows a mass spectrum of zirconium. The relative abundance, as a percentage from 0 to 100, is graphed on the y axis, and the mass to charge ratio is graphed on the x axis. The sample contains five different isomers of zirconium. Z R 90, which has a mass to charge ratio of 90, is the most abundant isotope at about 51 percent relative abundance. Z R 91 has a mass to charge ratio of 91 and a relative abundance of about 11 percent. Z R 92 has a mass to charge ratio of 92 and a relative abundance of about 18 percent. Z R 94 has a mass to charge ratio of 94 and a relative abundance of about 18 percent. Z R 96, which has a mass to charge ratio of 96, is the least abundant zirconium isotope with a relative abundance of about 2 percent. — Figura \(\PageIndex{5}\): El análisis del circonio en un espectrómetro de masas produce un espectro de masas con picos que muestran los diferentes isótopos de Zr.

La presencia y abundancia natural de los isótopos se puede determinar experimentalmente usando un instrumento llamado el espectrómetro de masas. La espectrometría de masas (EM) se usa ampliamente en química, medicina forense, medicina ambiental y muchos otros campos para analizar y ayudar a identificar las sustancias en una muestra de material. Típicamente, en un espectrómetro de masas (Figura \(\PageIndex{5}\)), la muestra se vaporiza y se expone a un haz de electrones de alta energía que hace que los átomos (o moléculas) de la muestra se carguen eléctricamente, y generalmente pierden uno o más electrones. Luego, estos cationes pasan a través de un campo eléctrico o magnético (variable) que desvía la trayectoria de cada catión, dependiendo de su masa y su carga (similar a la forma en que la trayectoria de un gran rodamiento de bolas de acero que pasan por un imán se desvía menos que la de un pequeño acero BB). Los iones se detectan y se crea un gráfico del número relativo de iones generados en función de sus relaciones de masa a carga (un espectro de masas). La altura de cada característica vertical o pico en un espectro de masas es proporcional a la fracción de cationes con la relación de masa a carga especificada. Desde su uso inicial, durante el desarrollo de la teoría atómica moderna, MS ha evolucionado para convertirse en una herramienta poderosa para el análisis químico en una amplia gama de aplicaciones.

Video \(\PageIndex{1}\): Vea este video de la Royal Society for Chemistry para una breve descripción de los rudimentos de la espectrometría de masas.

Resumen

Un átomo consiste en un núcleo pequeño, con carga positiva, rodeado de electrones. El núcleo contiene protones y neutrones; su diámetro es aproximadamente 100,000 veces más pequeño que el del átomo. La masa de un átomo generalmente se expresa en unidades de masa atómica (amu), que se conoce como la masa atómica. Un amu se define como exactamente \(1/12\) de la masa de un átomo de carbono-12 y es igual a 1.6605 \(\times\) 10⁻²⁴ g.

Los protones son partículas relativamente pesadas con una carga de 1+ y una masa de 1,0073 amu. Los neutrones son partículas relativamente pesadas sin carga y con una masa de 1,0087 amu. Los electrones son partículas ligeras con una carga de 1− y una masa de 0,00055 amu. El número de protones en el núcleo se llama el número atómico (Z) y es la propiedad que define la identidad elemental de un átomo. La suma de los números de protones y neutrones en el núcleo se llama el número de masa y se expresa en amu, es aproximadamente igual a la masa del átomo. Un átomo es neutral cuando contiene números iguales de electrones y protones.

Los isótopos de un elemento son átomos con el mismo número atómico pero diferentes números de masa; los isótopos de un elemento difieren solamente en el número de neutrones dentro del núcleo. Cuando un elemento natural está compuesto por varios isótopos, la masa atómica del elemento representa el promedio de las masas de los isótopos involucrados. Un símbolo químico identifica los átomos en una sustancia usando símbolos, que son abreviaturas de una, dos, o tres letras para los átomos.

Ecuaciones Claves

\(\mathrm{average\: mass}=\sum_{i}(\mathrm{fractional\: abundance \times isotopic\: mass})_i\)

Glosario

anión: átomo o molécula con carga negativa (contiene más electrones que protones)

masa atómica: masa promedio de los átomos de un elemento, expresada en amu

unidad de masa atómica (amu): (también, unidad de masa atómica unificada, u, o Dalton, Da) unidad de masa igual a \(\dfrac{1}{12}\) de la masa de un átomo ¹²C

número atómico (Z): Número de protones en el núcleo de un átomo.
catión

átomo o molécula con carga positiva (contiene menos electrones que protones)

símbolo químico: abreviatura de una, dos o tres letras utilizada para representar un elemento o sus átomos

Dalton (Da): Unidad alternativa equivalente a la unidad de masa atómica.

unidad fundamental de carga: (también llamada carga elemental) es igual a la magnitud de la carga de un electrón (e) con e = 1.602 \(\times\) 10⁻¹⁹ C

ion: átomo o molécula cargada eléctricamente (contiene números que no son iguales de protones y electrones)

número de masa (A): Suma de los números de neutrones y protones en el núcleo de un átomo.
unidad de masa atómica unificada (u): Unidad alternativa equivalente a la unidad de masa atómica.

Contribuyentes

Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.