3.1: La fórmula de masa y el concepto del mol
- Page ID
- 1811
habilidades para desarrollar
- Calcular masas de fórmula para compuestos covalentes y compuestos iónicos.
- Definir la cantidad de mole unitario y la cantidad relacionada con el número de Avogadro
- Explicar la relación entre masa, moles, y número de átomos o moléculas, y hacer cálculos que derivan estas cantidades de una a la otra.
Podemos argumentar que la química moderna comenzó cuando los científicos comenzaron a explorar los aspectos cuantitativos y cualitativos de la química. Por ejemplo, la teoría atómica de Dalton fue un intento de explicar los resultados de las mediciones que le permitieron calcular las masas relativas de elementos combinados en varios compuestos. Comprender la relación entre las masas de los átomos y las fórmulas químicas de los compuestos nos permite describir la composición de las sustancias cuantitativamente.
La fórmula de masa
En un capítulo anterior, describimos el desarrollo de la unidad de masa atómica, el concepto de masas atómicas promedio y el uso de fórmulas químicas para representar la composición elemental de las sustancias. Estas ideas se pueden extender para calcular la masa de la fórmula de una sustancia por sumando las masas atómicas promedio de todos los átomos representados en la fórmula de la sustancia.
La fórmula de masa para sustancias covalentes
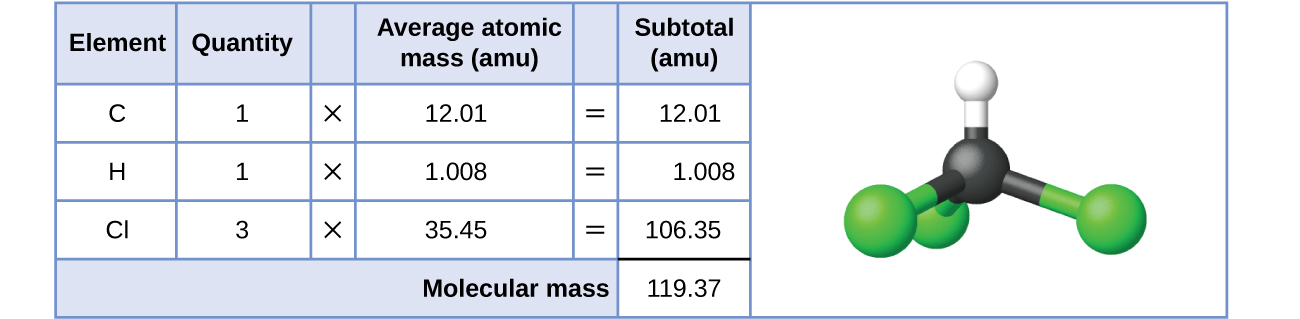
Para sustancias covalentes, la fórmula representa los números y tipos de átomos que componen una sola molécula de la sustancia; por eso la masa de fórmula se puede referir correctamente como una masa molecular. Considere el cloroformo (CHCl3), un compuesto covalente que se usaba como anestésico quirúrgico y que ahora se usa principalmente en la producción de tetrafluoroetileno, el componente básico del polímero "antiadherente", el teflón. La fórmula molecular del cloroformo indica que una sola molécula contiene un átomo de carbono, un átomo de hidrógeno y tres átomos de cloro. La masa molecular promedio de una molécula de cloroformo es igual a la suma de las masas atómicas promedio de estos átomos. La figura \(\PageIndex{1}\) describe los cálculos usados para derivar la masa molecular del cloroformo, que es 119.37 amu.
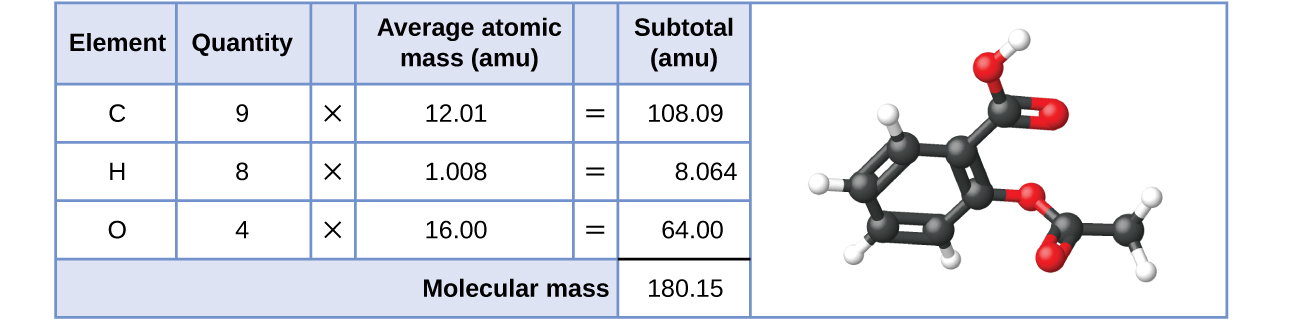
Igualmente, la masa molecular de una molécula de aspirina, C9H8O4, es la suma de las masas atómicas de nueve átomos de carbono, ocho átomos de hidrógeno, y cuatro átomos de oxígeno, que es 180,15 amu (Figura \(\PageIndex{2}\)).
Ejemplo \(\PageIndex{1}\): COMPUTACIÓN DE MASAS MOLECULARES PARA UN COMPUESTO COVALENTE
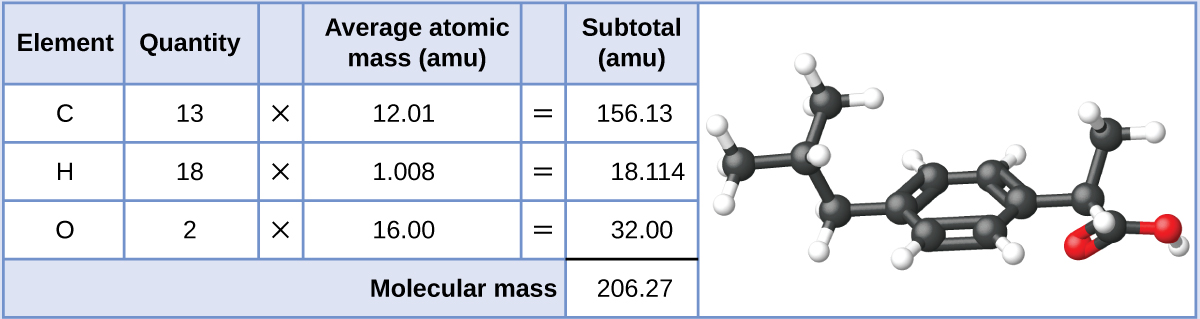
El Ibuprofeno, C13H18O, es un compuesto covalente y el ingrediente activo en varios medicamentos contra el dolor populares sin receta, como Advil y Motrin. ¿Cuál es la masa molecular (amu) para este compuesto?
Solución
Las moléculas de este compuesto están compuestas por 13 átomos de carbono, 18 átomos de hidrógeno, y 2 átomos de oxígeno. Siguiendo el enfoque descrito antes, la masa molecular promedio para este compuesto es:
Ejercicio \(\PageIndex{1}\)
El acetaminofeno, C8H9NO2, es un compuesto covalente y el ingrediente activo en varios medicamentos contra el dolor populares sin receta, como Tylenol. ¿Cuál es la masa molecular (amu) para este compuesto?
- Respuesta
-
151.16 amu
La fórmula de masa para los compuestos iónicos
Los compuestos iónicos están compuestos por cationes discretos y aniones combinados en proporciones para producir materia en masa eléctricamente neutra. La masa de fórmula para un compuesto iónico se calcula en el mismo modo que la masa de fórmula para compuestos covalentes: sumando las masas atómicas promedio de todos los átomos en la fórmula del compuesto. Sin embargo, tenga en cuenta que la fórmula para un compuesto iónico no representa la composición de una molécula discreta, por eso no se llama correctamente como la "masa molecular".
Como ejemplo, considere el cloruro de sodio, NaCl, el nombre químico de la sal de mesa común. El cloruro de sodio es un compuesto iónico compuesto por cationes de sodio, Na+ y aniones de cloruro, Cl−, combinados en una proporción de 1:1. La fórmula de la masa para este compuesto se calcula a ser 58,44 amu (Figura \(\PageIndex{3}\)).
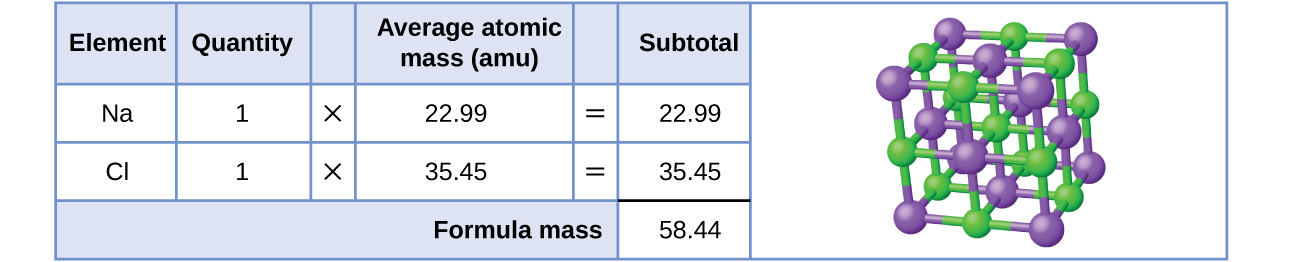
Tenga en cuenta que las masas promedio de sodio neutro y los átomos de cloro se usaron en este cálculo, en lugar de las masas para cationes de sodio y aniones de cloro. Este enfoque es perfectamente aceptable cuando se calcula la masa de la fórmula de un compuesto iónico. Aunque un catión de sodio tiene una masa un poco más pequeña que un átomo de sodio (ya que le falta un electrón), esta diferencia se compensará porque un anión de cloruro es un poco más masivo que un átomo de cloruro (debido al electrón adicional). Además, la masa de un electrón es despreciablemente pequeña con respecto a la masa de un átomo típico. Incluso cuando se calcula la masa de un ion aislado, los electrones faltantes o adicionales generalmente pueden se ignorar, ya que su contribución a la masa general es insignificante, reflejada solo en los dígitos no significativos que se perderán cuando la masa calculada se redondea correctamente. Las pocas excepciones a esta guía son los iones muy ligeros derivados de elementos con masas atómicas conocidas con precisión.
Ejemplo \(\PageIndex{2}\): COMPUTACIÓN DE MASA DE FÓRMULA PARA UN COMPUESTO IÓNICO
El sulfato de aluminio, Al2(SO4)3, es un compuesto iónico que se usa en la fabricación de papel y en varios procesos de purificación de agua. ¿Cuál es la fórmula de masa (amu) de este compuesto?
Solución
La fórmula para este compuesto indica que contiene iones de Al3+ y SO42− combinados en una proporción de 2:3. Para calcular una masa de fórmula, es útil reescribir la fórmula en el formato más simple, Al2S3O12. Siguiendo el enfoque descrito antes, la masa de fórmula para este compuesto se calcula de la siguiente manera:
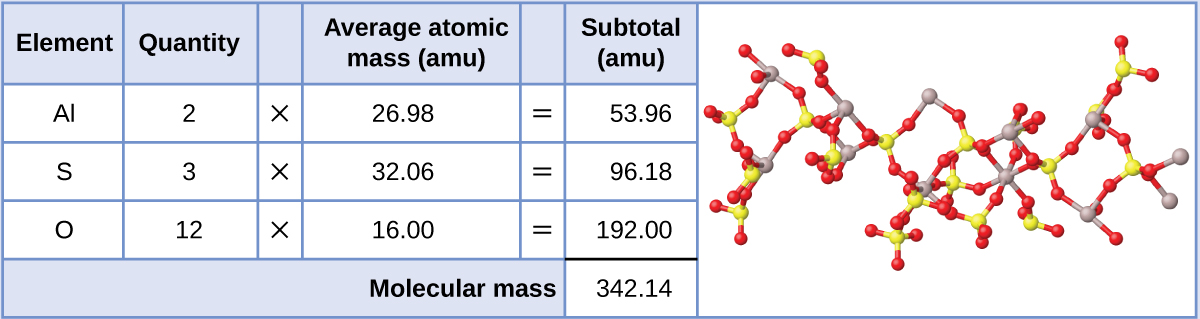
Ejercicio \(\PageIndex{2}\)
El fosfato de calcio, Ca3(PO4)2, es un compuesto iónico y un agente antiaglomerante común que se agrega a los productos de comida. ¿Cuál es la fórmula de masa (amu) de fosfato de calcio?
- Respuesta
-
310.18 amu
El mol
La identidad de una sustancia no se define solamente por los tipos de átomos o iones que contiene, sino también por la cantidad de cada tipo de átomo o ion. Por ejemplo, el agua, el H2O, y el peróxido de hidrógeno, H2O2, son similares porque sus moléculas están compuestas de átomos de hidrógeno y de oxígeno. Sin embargo, debido a que una molécula de peróxido de hidrógeno contiene dos átomos de oxígeno, a diferencia de la molécula de agua, que tiene solo uno, las dos sustancias tienen propiedades muy diferentes. Hoy en día, contamos con instrumentos sofisticados que permiten la medición directa de estos rasgos microscópicos definitorios; sin embargo, los mismos rasgos se derivaron originalmente de la medición de las propiedades macroscópicas (las masas y los volúmenes de grandes cantidades de materia) usando herramientas relativamente simples (balanzas y artículos de vidrio volumétricos). Este enfoque experimental requirió la introducción de una nueva unidad para la cantidad de sustancias, el mole, que sigue siendo indispensable en la química moderna.
El mol es una unidad de cantidad similar a las unidades familiares como pares, docenas, etc. El mol da una medida específica del número de átomos o moléculas en una muestra masiva de materia. Un mol se define como la cantidad de sustancia que contiene el mismo número de entidades discretas (como átomos, moléculas y también iones). El número de átomos en una muestra de 12C puro que pesa exactamente 12 g. Una connotación latina para la palabra "mole" es "gran masa" o "granel", que es consistente con su uso como el nombre de esta unidad. El mole da un vínculo entre una propiedad macroscópica, una masa aparente y una propiedad fundamental muy importante, el número de átomos, moléculas, etc.
Se ha determinado experimentalmente que el número de entidades que componen el mol es \(6.02214179\times10^{23}\), un constante fundamental que se llama número de Avogadro (NA) o el constante de Avogadro en honor del científico italiano Amedeo Avogadro. Este constante se informa correctamente con una unidad explícita de "por mol", una versión convenientemente redondeada que es
Consistente con su definición como unidad de cantidad, 1 mol de cualquier elemento contiene el mismo número de átomos que 1 mol de cualquier otro elemento. Sin embargo, las masas de 1 mol de diferentes elementos son diferentes, ya que las masas de los átomos individuales son drásticamente diferentes. La masa molar de un elemento (o compuesto) es la masa en gramos de 1 mol de esa sustancia, una propiedad expresada en unidades de gramos por mol (g / mol) (Figura \(\PageIndex{4}\)).

Debido a que las definiciones del mol y de la unidad de masa atómica se basan en la misma sustancia de referencia, 12C, la masa molar de cualquier sustancia es numéricamente equivalente a su peso atómico o fórmula en amu. Según la definición de amu, un solo átomo 12C pesa 12 amu (su masa atómica es 12 amu). Según la definición del mol, 12 g de 12C contienen 1 mol de 12C átomos (su masa molar es 12 g/mol). Esta relación es válida para todos los elementos, porque sus masas atómicas se miden en relación con la de la sustancia de referencia amu, 12C. Extendiendo este principio, la masa molar de un compuesto en gramos también es numéricamente equivalente a su masa de fórmula en amu (Figura \(\PageIndex{5}\)).

| Elemento | Masa Atómica Promedio (amu) | Masa Molar (g/mol) | Átomos/Mole |
|---|---|---|---|
| C | 12,01 | 12,01 | \(6.022 \times 10^{23}\) |
| H | 1,008 | 1,008 | \(6.022 \times 10^{23}\) |
| O | 16,00 | 16,00 | \(6.022 \times 10^{23}\) |
| Na | 22,99 | 22,99 | \(6.022 \times 10^{23}\) |
| Cl | 33,45 | 35,45 | \(6.022 \times 10^{23}\) |
La masa atómica y la masa molar son numéricamente equivalentes, tenga en cuenta que son muy diferentes en términos de escala, esto se representa en la diferencia de las magnitudes de sus unidades respectivas (amu versus g). Para apreciar la enormidad del mole, considere una pequeña gota de agua después de una lluvia. Aunque esto representa solo una pequeña fracción de 1 mol de agua (~ 18 g), contiene más moléculas de agua de lo que se puede imaginar claramente. Si las moléculas se distribuyeran equitativamente entre los aproximadamente siete mil millones de personas en la tierra, cada persona recibiría más de 100 mil millones de moléculas.
Vídeo \(\PageIndex{1}\): El mole se usa en química para representar \(6.022\times10^{23}\) de algo, pero puede ser difícil conceptualizar un número tan grande. Mire este video y luego complete las preguntas de "Think" que siguen. Explore más sobre el mole por revisando la información en "Dig Deeper".
Las relaciones entre la fórmula de masa, el mole, y el número de Avogadro se pueden aplicar para calcular varias cantidades que describen la composición de sustancias y compuestos. Por ejemplo, si conocemos la masa y la composición química de una sustancia, podemos determinar el número de moles y calcular el número de átomos o moléculas en la muestra. Del mismo modo, si conocemos el número de moles de una sustancia, podemos derivar el número de átomos o moléculas y calcular la masa de la sustancia.
Ejemplo \(\PageIndex{3}\): DERIVANDO MOLES DE GRAMOS PARA UN ELEMENTO
De acuerdo con las reglas nutricionales del Departamento de Agricultura de los EE.UU., El requerimiento promedio estimado de potasio en la dieta es de 4,7 g. ¿Cuál es el requerimiento promedio estimado de potasio en moles?
Solución
Se da la masa de K y se solicita la cantidad correspondiente de K en moles. En referencia a la tabla periódica, la masa atómica de K es de 39,10 amu, por lo que su masa molar es de 39,10 g / mol. La masa dada de K (4,7 g) es un poco más de una décima parte de la masa molar (39,10 g), por lo que una estimación razonable de la cantidad de moles sería un poco más que 0,1 mol.
La cantidad molar de una sustancia se puede calcular dividiendo su masa (g) por su masa molar (g/mol):

El método de etiqueta de factor apoya este enfoque matemático, la unidad "g" se cancela y la respuesta tiene unidades de “mol:”
\[ \mathrm{4.7\; \cancel{g} K \left ( \dfrac{mol\; K}{39.10\;\cancel{g}}\right)=0.12\;mol\; K} \nonumber\]
La magnitud calculada (0.12 mol K) es consistente con nuestra expectativa, ya que es un poco más que 0.1 mol.
Ejercicio \(\PageIndex{3}\): BerIlio
El Berilio es un metal ligero usado para fabricar ventanas de rayos X transparentes para instrumentos de imágenes médicos. ¿Cuántos moles de Be hay en una ventana de lámina delgada que pesa 3,24 g?
Respuesta
0,360 mol
Ejemplo \(\PageIndex{4}\): Derivando Gramos de Moles Para un Elemento
Un litro de aire contiene \(9.2\veces10^{-4}\) mol argón. ¿Cuál es la masa de Ar en un litro de aire?
Solución
La cantidad molar de Ar se da, y se debe utilizar para derivar la masa correspondiente en gramos. Ya que la cantidad de Ar es menos que 1 mol, la masa será menor que la masa de 1 mol de Ar, aproximadamente 40 g. La cantidad molar en cuestión es aproximadamente una milésima (~ 10−3) de un mol, y por eso la masa correspondiente debe ser aproximadamente una milésima parte de la masa molar (~0,04 g):

En este caso, la lógica dicta (y el método de etiquetado de factor es compatible) multiplicando la cantidad dada (mol) por la masa molar (g/mol):
\[\mathrm{9.2 \times10^{-4}\; \cancel{mol} \; Ar \left( \dfrac{39.95\;g}{\cancel{mol}\;Ar} \right)=0.037\;g\; Ar} \nonumber\]
El resultado está de acuerdo con nuestras expectaciones, alrededor de 0,04 g Ar.
Ejercicio \(\PageIndex{4}\)
¿Cuál es la masa de 2,561 mol de oro?
- Respuesta
-
504,4 g
ejemplo \(\PageIndex{6}\): DERIVANDO EL NÚMERO DE ÁTOMOS DE LA MASA PARA UN ELEMENTO
El cobre se usa comúnmente para fabricar cables eléctricos (Figura \(\PageIndex{6}\)). ¿Cuántos átomos de cobre hay en 5,00 g de alambre de cobre?

Solución
El número de átomos de Cu en el cable se puede derivar convenientemente de su masa por un cálculo de dos pasos: primero calculando la cantidad molar de Cu y luego usando el número de Avogadro (NA) para convertir esta cantidad molar a el número de átomos de Cu:

Considerando que la masa de la muestra dada (5,00 g) es un poco menos de una décima parte de la masa de 1 mol de Cu (~ 64 g), una estimación razonable para el número de átomos en la muestra sería del orden de uno décimo NA, o aproximadamente 1022 átomos de Cu. Haciendo los cálculos en dos pasos:
\[\mathrm{5.00\:\cancel{g}\:Cu\left(\dfrac{\cancel{mol}\:Cu}{63.55\:\cancel{g}}\right)\left(\dfrac{6.022\times10^{23}\:atoms}{\cancel{mol}}\right)=4.74\times10^{22}\:atoms\: of\: copper}\]
El método de etiqueta de factor produce la cancelación deseada de unidades, y el resultado calculado es del orden de 1022 como se esperaba.
ejercicio \(\PageIndex{6}\)
Un buscador de oro en un río recolecta 15,00 g de oro puro. ¿Cuántos átomos de Au hay en esta cantidad de oro?
- Respuesta
-
\(4.586 \times 10^{22}\; Au\) atoms
Ejemplo \(\PageIndex{7}\): DERIVANDO MOLES DE GRAMOS PARA UN COMPUESTO
Nuestros cuerpos sintetizan proteínas de aminoácidos. Uno de estos aminoácidos es la glicina, que tiene la fórmula molecular C2H5O2N. ¿Cuántos moles de moléculas de glicina hay en 28,35 g de glicina?
Solución
Podemos deducir el número de moles de un compuesto de su masa siguiendo el mismo procedimiento que usamos para un elemento en Ejemplo \(\PageIndex{6}\):

La masa molar de glicina se requiere para este cálculo, y se calcula de la misma manera que su masa molecular. Un mol de glicina, C2H5O2N, contiene 2 moles de carbono, 5 moles de hidrógeno, 2 moles de oxígeno, y 1 mol de nitrógeno
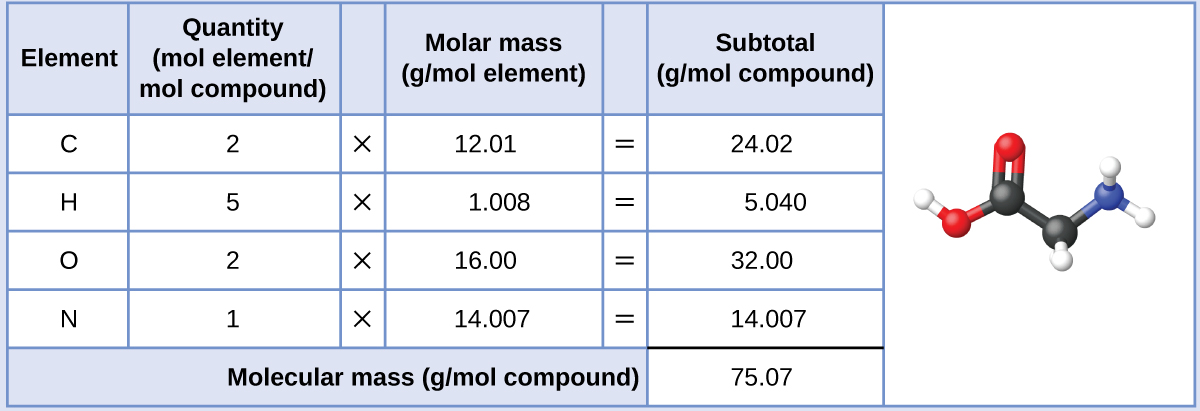
La masa de glicina dada (~28 g) es un poco más de un tercio de la masa molar (~75 g/mol), por eso esperamos que el resultado calculado sea un poco mayor que un tercio de un mol (~0,33 mol). Dividiendo la masa del compuesto por sus rendimientos de masa molar:
\[\mathrm{28.35\:\cancel{g}\:glycine\left(\dfrac{mol\: glycine}{75.07\:\cancel{g}}\right)=0.378\:mol\: glycine} \nonumber\]
Este resultado es consistente con nuestra estimación aproximada.
Ejercicio \(\PageIndex{7}\)
¿Cuántos moles de sacarosa, \(C_{12}H_{22}O_{11}\), hay en una muestra de 25 g de sacarosa?
- Respuesta
-
0,073 mol
Ejemplo \(\PageIndex{8}\): DERIVANDO GRAMOS DE MOLES PARA UN COMPUESTO
La vitamina C es un compuesto covalente con la fórmula molecular C6H8O6. La cantidad diaria recomendada de vitamina C para niños de 4 a 8 años es de 1,42 × 10−4 mol. ¿Cuál es la masa de esta recomendación de vitamina C en gramos?
Solución
Para los elementos, la masa de un compuesto se puede derivar de su cantidad molar como se muestra aquí:

La masa molar para este compuesto se calcula a ser 176.124 g/mol. El número dado de moles es una fracción muy pequeña de un mole (~10−4 o una décima milésima); por lo tanto, esperaríamos que la masa correspondiente sea aproximadamente una diez milésima parte de la masa molar (~0,02 g). Al hacer la calculación, obtenemos:
Esto es consistente con el resultado anticipado.
Ejercicio \(\PageIndex{8}\)
¿Cuál es la masa de 0,443 mol de hidracina, \(N_2H_4\)?
- Respuesta
-
14,2 g
Ejemplo \(\PageIndex{9}\): DERIVANDO EL NÚMERO DE MOLÉCULAS DE LA MASA DEL COMPUESTO
Un paquete de un endulzante artificial contiene 40,0 mg de sacarina (C7H5NO3S), que tiene la fórmula estructural:
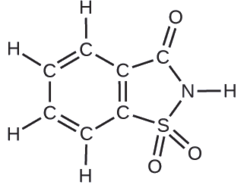
Dado que la sacarina tiene una masa molar de 183,18 g/mol, ¿Cuántas moléculas de sacarina hay en una muestra de sacarina de 40,0 mg (0.0400-g)? ¿Cuántos átomos de carbono hay en la misma muestra?
Solución
El número de moléculas en una masa dada de compuesto se calcula primero derivando el número de moles, como se muestra en el Ejemplo \(\PageIndex{8}\), y luego se multiplica por el número de Avogadro:

Usando la masa dada y la masa molar para los rendimientos de sacarina:
\[\mathrm{0.0400\:\cancel{g}\:\ce{C7H5NO3S}\left(\dfrac{\cancel{mol}\:\ce{C7H5NO3S}}{183.18\:\cancel{g}\:\ce{C7H5NO3S}}\right)\left(\dfrac{6.022\times10^{23}\:\ce{C7H5NO3S}\:molecules}{1\:\cancel{mol}\:\ce{C7H5NO3S}}\right)}\\
=\mathrm{1.31\times10^{20}\:\ce{C7H5NO3S}\:molecules}\]
La fórmula del compuesto muestra que cada molécula contiene siete átomos de carbono, por eso el número de átomos de C en la muestra dada es:
\[\mathrm{1.31\times10^{20}\:\ce{C7H5NO3S}\: molecules\left(\dfrac{7\:C\: atoms}{1\:\ce{C7H5NO3S}\: molecule}\right)=9.20\times10^{21}\:C\: atoms} \nonumber\]
ejercicio \(\PageIndex{9}\)
¿Cuántas moléculas de \(C_4H_{10}\) hay en 9,213 g de este compuesto? ¿Cuántos átomos de hidrógeno hay?
- Respuesta
-
- \(9.545 \times 10^{22}\; \text{molecules}\; C_4H_{10}\)
- \(9.545 \times 10^{23 }\;\text{atoms}\; H\)
Resumen
La masa de fórmula de una sustancia es la suma de las masas atómicas promedio de cada átomo representado en la fórmula química y se expresa en unidades de masa atómica. La masa de fórmula de un compuesto covalente también se conoce como masa molecular. Una unidad de cantidad conveniente para expresar un gran número de átomos o moléculas es el mol. Las mediciones experimentales han determinado que la cantidad de entidades que componen 1 mol de sustancia es 6,022 × 1023, una cantidad llamada número de Avogadro. La masa en gramos de 1 mol de sustancia es su masa molar. Debido al uso de la misma sustancia de referencia para definir la unidad de masa atómica y el mol, la masa de fórmula (amu) y la masa molar (g/mol) para cualquier sustancia son numéricamente equivalentes (por ejemplo, una molécula de H2O pesa aproximadamente 18 amu y 1 mol de moléculas de H2O pesa aproximadamente 18 g).
Notas al pie de la página
- 1 Omiatek, Donna M., Amanda J. Bressler, Ann-Sofie Cans, Anne M. Andrews, Michael L. Heien, and Andrew G. Ewing. “The Real Catecholamine Content of Secretory Vesicles in the CNS Revealed by Electrochemical Cytometry.” Scientific Report 3 (2013): 1447, accessed January 14, 2015, doi:10.1038/srep01447.
Glosario
- Número de Avogadro (NA)
- Valor determinado experimentalmente del número de entidades que componen 1 mol de sustancia, igual a 6.022 × 1023 mol−1
- fórmula de masa
- Suma de las masas promedio para todos los átomos representados en una fórmula química; para los compuestos covalentes, esta también es la masa molecular.
- mol
- Cantidad de sustancia que contiene el mismo número de átomos, moléculas, iones y también otras entidades que el número de átomos en exactamente 12 gramos de 12C.
- masa molar
- Masa en gramos de 1 mol de una sustancia.
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


