6.1: La energía electromagnética

HABILIDADES PARA DESARROLLAR

• Explicar el comportamiento básico de las ondas, incluidas las ondas viajeras y las ondas estacionarias.
• Describir la naturaleza ondulatoria de la luz.
• Usar las ecuaciones apropiadas para calcular las propiedades de onda de luz relacionadas, como el período, la frecuencia, la longitud de onda y la energía
• Distinguir entre línea y espectros de emisión continua.
• Describir la naturaleza de la partícula de la luz.

La naturaleza de la luz ha sido objeto de investigaciones desde la antigüedad. En el siglo XVII, Isaac Newton hizo experimentos con lentes y prismas y pudo demostrar que la luz blanca consiste en los colores individuales del arco iris combinados. Newton explicó sus hallazgos ópticos en términos de una visión "corpuscular" de la luz, en la que la luz estaba compuesta de flujos de partículas muy pequeñas que viajaban a altas velocidades de acuerdo con las leyes del movimiento de Newton. Otros en el siglo XVII, como Christiaan Huygens, habían demostrado que fenómenos ópticos como la reflexión y la refracción se podrían explicar igualmente en términos de luz como ondas que viajan a gran velocidad a través de un medio llamado "éter luminífero" que se pensaba que impregnaba todo el espacio. A principios del siglo XIX, Thomas Young demostró que la luz que pasaba a través de rendijas estrechas y muy separadas producía patrones de interferencia que no se podían explicar en términos de partículas newtonianas, pero sí se podían explicar fácilmente en términos de ondas. En el siglo XIX, después de que James Clerk Maxwell desarrolló su teoría de la radiación electromagnética y demostró que la luz era la parte visible de un vasto espectro de ondas electromagnéticas, la visión de la luz por las partículas se desacreditó por completo. A fines del siglo XIX, los científicos consideraban que el universo físico abarcaba aproximadamente dos dominios separados: materia compuesta por partículas que se mueven de acuerdo con las leyes del movimiento de Newton, y radiación electromagnética que consiste en ondas dominadas por las ecuaciones de Maxwell. Hoy en día, estos dominios se llaman la mecánica clásica y la electrodinámica clásica (o el electromagnetismo clásico). Aunque había algunos fenómenos físicos que no se podían explicar dentro de estos dominios, los científicos en ese momento estaban tan seguros de la solidez general de estos dominios que vieron estas aberraciones como paradojas desconcertantes que finalmente se resolverán de alguna manera dentro de estos dominios. Como veremos, estas paradojas llevaron a una estructura contemporáneo que conecta íntimamente las partículas y las ondas en un nivel fundamental llamado la dualidad onda-partícula, que ha superado la visión clásica.

La luz visible y otras formas de radiación electromagnética tienen una parte importante en la química, ya que se pueden usar para inferir las energías de los electrones dentro de los átomos y las moléculas. Gran parte de la tecnología moderna se basa en la radiación electromagnética. Por ejemplo, las ondas de radio de un teléfono móvil, los rayos X usados por los dentistas, la energía usada para cocinar alimentos en su microondas, el calor radiante de los objetos al rojo vivo, y la luz de la pantalla de su televisor son formas de radiación electromagnética que exhiben un comportamiento similar a una onda.

Las ondas

Una onda es una oscilación o un movimiento periódico que puede transportar energía de un punto en el espacio a otro punto. Ejemplos comunes de olas están a nuestro alrededor. Sacudiendo la orilla de una cuerda transfiere energía de su mano al otro extremo de la cuerda, dejar caer una piedra en un estanque hace que las ondas se ondulen hacia afuera a lo largo de la superficie del agua, y la expansión del aire que acompaña a un rayo genera ondas de sonido (trueno), que puede viajar hacia afuera por varias millas. En cada uno de estos casos, la energía cinética se transfiere a través de la materia (la cuerda, el agua, o el aire), mientras que la materia permanece esencialmente en su lugar. Un ejemplo perspicaz de una ola ocurre en los estadios deportivos cuando los fanáticos en una región estrecha de asientos se levantan simultáneamente y se paran con sus brazos levantados por unos segundos antes de sentarse nuevamente, mientras que los fanáticos en las secciones vecinas también se levantan y se sientan en secuencia. Esta ola puede rodear rápidamente un gran estadio en unos pocos segundos, pero ninguno de los fanáticos en realidad viaja con la ola, todos permanecen en sus asientos o por encima de ellos.

Las ondas no necesitan estar restringidas para viajar a través de la materia. Como mostró Maxwell, las ondas electromagnéticas consisten en un campo eléctrico que oscila en el paso con un campo magnético perpendicular, los cuales son perpendiculares a la dirección de desplazamiento. Estas ondas pueden viajar a través de un vacío a una velocidad constante de 2.998 × 10⁸ m/s, la velocidad de la luz (indicada por c).

Todas las ondas, incluyendo las formas de radiación electromagnética, se caracterizan por una longitud de onda (indicada por λ, la letra griega minúscula lambda), una frecuencia (indicada por ν, la letra griega minúscula nu) y una amplitud. Como se puede ver en la Figura \(\PageIndex{1}\), la longitud de onda es la distancia entre dos picos o valles consecutivos en una onda (medida en metros en el sistema SI). Las ondas electromagnéticas tienen longitudes de onda que caen dentro de un rango enorme de longitudes de onda de kilómetros (10³ m) a picómetros (10⁻¹² m) que se han observado. La frecuencia es el número de ciclos de onda que pasan un punto específico en el espacio en una cantidad específica de tiempo (en el sistema SI, esto se mide en segundos). Un ciclo corresponde a una longitud de onda completa. La unidad para la frecuencia, expresada en ciclos por segundo [s ⁻¹], es el hercio (Hz). Los múltiplos comunes de esta unidad son megahertz, (1 MHz = 1 × 10⁶ Hz) y gigahertz (1 GHz = 1 × 10⁹ Hz). La amplitud corresponde a la magnitud del desplazamiento de la onda y, por lo tanto, en la Figura, esto corresponde a la mitad de la altura entre los picos y los valles. La amplitud está relacionada con la intensidad de la onda, que para la luz es el brillo, y para el sonido es la intensidad.

Figura \(\PageIndex{1}\): Las ondas sinusoidales unidimensionales muestran la relación entre la longitud de onda, la frecuencia y la velocidad. La onda con la longitud de onda más corta tiene la frecuencia más alta. La amplitud es la mitad de la altura de la onda desde el pico hasta el canal.

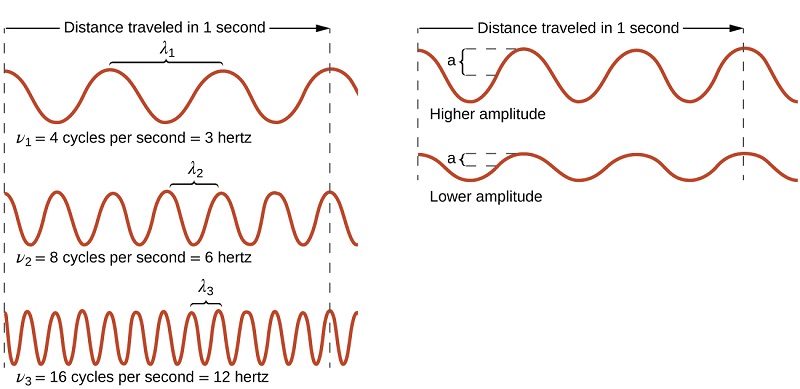
El producto de la longitud de onda (λ) y su frecuencia (ν), λν, es la velocidad de la onda. Así, para la radiación electromagnética en el vacío:

\[c=\mathrm{2.998×10^8\,ms^{−1}}=λν \label{6.2.1}\]

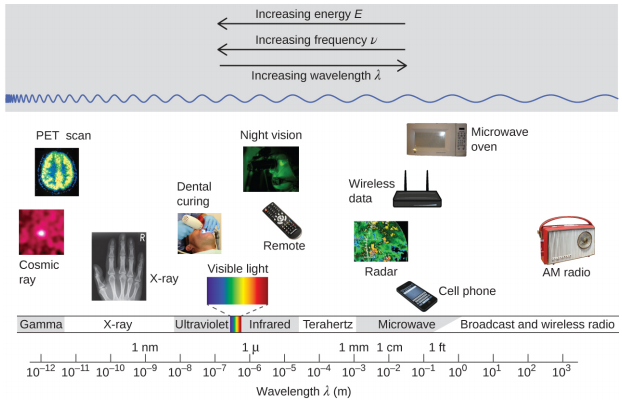
La longitud de la onda y la frecuencia son inversamente proporcionales: a medida que aumenta la longitud de onda, la frecuencia disminuye. La proporcionalidad inversa se ilustra en la Figura \(\PageIndex{2}\). Esta figura también muestra el espectro electromagnético, el rango de todos los tipos de radiación electromagnética. Cada uno de los diversos colores de la luz visible tiene frecuencias y longitudes de onda específicas asociadas, y se puede ver que la luz visible constituye sólo una pequeña parte del espectro electromagnético. Debido a que las tecnologías desarrolladas para trabajar en varias partes del espectro electromagnético son diferentes, por razones de conveniencia y legados históricos, las diferentes unidades se usan típicamente para diferentes partes del espectro. Por ejemplo, las ondas de radio generalmente se especifican como frecuencias (generalmente en unidades de MHz), mientras que la región visible generalmente se especifica en longitudes de onda (típicamente en unidades de nm o angstroms).

Figura \(\PageIndex{2}\): Las partes del espectro electromagnético se muestran en orden de frecuencia decreciente y de longitud de onda creciente. Los ejemplos de algunas aplicaciones para varias longitudes de onda incluyen tomografías por emisión de positrones (PET), imágenes de rayos X, controles remotos, Internet inalámbrico, teléfonos celulares y radios. (Crédito "Cosmic ray": modificación del trabajo de la NASA; crédito "PET scan": modificación del trabajo del Instituto Nacional de la Salud; crédito "X-ray": modificación del trabajo del Dr. Jochen Lengerke; crédito "Dental curing" : modificación del trabajo por el Departamento de la Marina; crédito "Visión nocturna": modificación del trabajo por el Departamento del Ejército; crédito "Remoto": modificación del trabajo por Emilian Robert Vicol; crédito "Teléfono celular": modificación del trabajo por Brett Jordan; crédito "Microondas": modificación del trabajo de Billy Mabray; crédito "Ultrasonido": modificación del trabajo de Jane Whitney; crédito "AM radio": modificación del trabajo de Dave Clausen)

Ejemplo \(\PageIndex{1}\): DETERMINACIÓN DE LA FRECUENCIA Y LA ONDA DE LA RADIACIÓN

Una farola de sodio emite una luz amarilla que tiene una longitud de onda de 589 nm (1 nm = 1 × 10⁻⁹ m). ¿Cuál es la frecuencia de esta luz?

Solución

Podemos reorganizar la Ecuación \ref{6.2.1} para resolver la frecuencia:

\[\nu=\dfrac{c}{λ}\]

Como c se expresa en metros por segundo, también debemos convertir 589 nm a metros.

\[\nu=\mathrm{\left(\dfrac{2.998×10^8\:\cancel{m}s^{−1}}{589\cancel{nm}}\right)\left(\dfrac{1×10^9\cancel{nm}}{1\cancel{m}}\right)=5.09×10^{14}\,s^{−1}}\]

Ejercicio \(\PageIndex{1}\)

Una de las frecuencias usadas para transmitir y recibir señales de teléfonos celulares en los Estados Unidos es de 850 MHz. ¿Cuál es la longitud de onda en metros de estas ondas de radio?

Respuesta

0.353 m = 35.3 cm

La comunicación inalámbrica

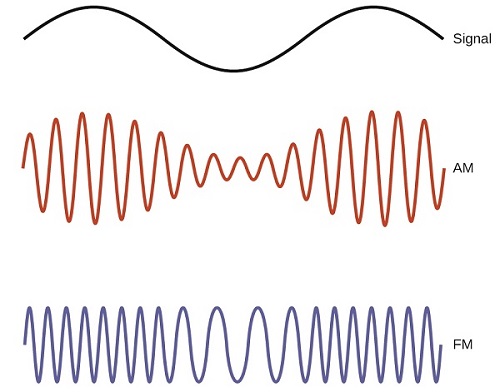
Muchas tecnologías valiosas operan en la región de frecuencia de radio (3 kHz-300 GHz) del espectro electromagnético. En el extremo de baja frecuencia (baja energía, longitud de onda larga) de esta región están las señales de radio AM (modulación de amplitud) (540-2830 kHz) que pueden viajar largas distancias. Las señales de radio FM (modulación de frecuencia) se usan en frecuencias más altas (87.5-108.0 MHz). En la radio AM, la información se transmite variando la amplitud de la onda (Figura \(\PageIndex{5}\)). En la radio FM, por el contrario, la amplitud es constante y la frecuencia instantánea varía.

Figura \(\PageIndex{3}\): Las torres de radio y celulares se utilizan normalmente para transmitir radiación electromagnética de longitud de onda larga. Cada vez más, las torres celulares están diseñadas para mezclarse con el paisaje, como con la torre celular de Tucson, Arizona (derecha), disfrazada de una palmera. (Crédito restante: modificación del trabajo por Sir Mildred Pierce; crédito medio: modificación del trabajo por M.O. Stevens)

Otras tecnologías también operan en la porción de ondas de radio del espectro electromagnético. Por ejemplo, las señales de los teléfonos celulares 4G son de aproximadamente 880 MHz, mientras que las señales del Sistema de Posicionamiento Global (GPS) operan a 1.228 y 1.575 GHz, las redes de tecnología inalámbrica de área local (Wi-Fi) operan a 2.4 a 5 GHz, y los sensores de peaje en las carreteras funcionan a 5.8 GHz. Las frecuencias asociadas con estas aplicaciones son convenientes porque tales ondas tienden no ser absorbidas mucho por los materiales de construcción comunes.

Figura \(\PageIndex{4}\): Este esquema describe cómo la modulación de amplitud (AM) y la modulación de frecuencia (FM) se pueden usar para transmitir una onda de radio.

Un fenómeno particularmente característico de las ondas se produce cuando dos o más ondas entran en contacto: interfieren entre sí. La figura \(\PageIndex{5}\) muestra los patrones de interferencia que pasan cuando la luz pasa a través de rendijas estrechas muy separadas aproximadamente en una longitud de onda. Los patrones de flecos producidos dependen de la longitud de la onda, con las franjas espaciadas más estrechamente para que la luz de longitud de onda más corta pase a través de un conjunto dado de rendijas. Cuando la luz pasa a través de las dos rendijas, cada rendija actúa efectivamente como una nueva fuente, lo que hace que dos ondas muy próximas entren en contacto con el detector (la cámara en este caso). Las regiones oscuras en la Figura \(\PageIndex{5}\) corresponden a regiones donde los picos de la onda de una ranura coinciden con los canales de la onda de la otra ranura (interferencia destructiva), mientras que las regiones más brillantes corresponden a las regiones donde coinciden los picos de las dos ondas (o sus dos canales) (interferencia constructiva). Del mismo modo, cuando dos piedras se lanzan juntas en un estanque, los patrones de interferencia son visibles en las interacciones entre las ondas producidas por las piedras. Tales patrones de interferencia no se pueden explicar por las partículas que se mueven de acuerdo con las leyes de la mecánica clásica.

Figura \(\PageIndex{5}\): Los patrones de franjas de interferencia se muestran para la luz que pasa a través de dos rendijas estrechas y muy próximas entre sí. El espaciado de las franjas depende de la longitud de la onda, con las franjas más espaciadas para la luz azul de longitud de onda más corta. (crédito: PASCO)

Dorothy Hodgkin

Debido a que las longitudes de la onda de los rayos X (10-10,000 picómetros [pm]) son comparables al tamaño de los átomos, los rayos X se pueden usar para determinar la estructura de las moléculas. Cuando un haz de rayos X pasa a través de moléculas agrupadas en un cristal, los rayos X chocan con los electrones y se dispersan. La interferencia constructiva y destructiva de estos rayos X dispersos crea un patrón de difracción específico. Haciendo calculaciones usando este patrón, las posiciones de cada uno de los átomos en la molécula se pueden determinar con mucha precisión. Una de las pioneras que ayudó a crear esta tecnología fue Dorothy Crowfoot Hodgkin.

Nació en El Cairo, Egipto, en 1910, donde sus padres británicos estaban estudiando arqueología. Incluso cuando era una niña, estaba fascinada con los minerales y los cristales.Cuando estudió en la Universidad de Oxford, comenzó a investigar cómo se podía usar la cristalografía de rayos X para determinar la estructura de las biomoléculas. Inventó nuevas técnicas que le permitieron a ella y a sus estudiantes determinar las estructuras de la vitamina B₁₂, la penicilina, y muchas otras moléculas importantes. La diabetes, una enfermedad que afecta a 382 millones de personas en todo el mundo, involucra la hormona insulina. Hodgkin comenzó a estudiar la estructura de la insulina en 1934, pero requirió varias décadas de avances en el campo antes de que finalmente informará sobre la estructura en 1969. La comprensión de la estructura ha permitido comprender mejor la enfermedad y las opciones para el tratamiento.

No todas las olas son olas viajeras. Las ondas estacionarias (también conocidas como ondas estacionarias) permanecen constreñidas dentro de alguna región del espacio. Como veremos, las ondas estacionarias desempeñan son importantes en nuestra comprensión de la estructura electrónica de los átomos y las moléculas. El ejemplo más simple de una onda estacionaria es una onda unidimensional asociada con una cuerda vibrante que se mantiene fija en sus dos puntos finales. La figura \(\PageIndex{6}\) muestra las cuatro ondas estacionarias de menor energía (la onda fundamental y los tres armónicos más bajos) para una cuerda vibrante a una amplitud particular. Aunque el movimiento de la cuerda se encuentra principalmente dentro de un plano, se considera que la onda en sí es unidimensional, ya que se encuentra a lo largo de la longitud de la cuerda. El movimiento de los segmentos de cuerda en una dirección perpendicular a la longitud de la cuerda genera las ondas, por lo que la amplitud de las ondas es visible como el desplazamiento máximo de las curvas que se ve en la Figura \(\PageIndex{6}\). La observación clave de la figura es que solo se pueden formar las ondas que tienen un número entero, n, de longitudes de onda medias entre los puntos finales. Un sistema con puntos finales fijos como éste restringe el número y el tipo de las posibles formas de ondas. Este es un ejemplo de cuantización, en el que solo se observan valores discretos de un conjunto más general de valores continuos de alguna propiedad. Otra observación importante es que las ondas armónicas (aquellas ondas que muestran más de la mitad de la longitud de onda) tienen una o más puntos entre los dos puntos finales que no están en movimiento. Estos puntos especiales son nodos. Las energías de las ondas estacionarias con una amplitud dada en una cuerda vibrante aumentan con el número de medias longitudes de onda n. Como el número de nodos es n - 1, también se puede decir que la energía depende del número de nodos, generalmente aumentando a medida que aumenta el número de nodos.

Figura \(\PageIndex{6}\): Una cuerda vibrante muestra algunas ondas estacionarias unidimensionales. Dado que los dos puntos finales de la cadena se mantienen fijos, solo se pueden formar ondas con un número entero de medias longitudes de onda. Los puntos en la cadena entre los puntos finales que no se mueven se llaman nodos.

Un ejemplo de ondas estacionarias bidimensionales se muestra en la Figura \(\PageIndex{7}\) que muestra los patrones de vibración en una superficie plana. Aunque las amplitudes vibracionales no se pueden ver cómo se podrían ver en la cuerda vibrante, los nodos se han hecho visibles rociando la superficie del tambor con un polvo que se acumula en las áreas de la superficie que tienen un desplazamiento mínimo. Para las ondas estacionarias unidimensionales, los nodos son puntos en la línea, pero para las ondas estacionarias bidimensionales, los nodos son líneas en la superficie (para las ondas estacionarias tridimensionales, los nodos son superficies bidimensionales dentro de la línea tridimensional). volumen). Debido a la simetría circular de la superficie del tambor, sus condiciones de contorno (la superficie del tambor está estrechamente restringida a la circunferencia del tambor) dan como resultado dos tipos de nodos: nodos radiales que barren todos los ángulos a radios constantes y, por lo tanto, se ven como círculos alrededor del centro, y nodos angulares que barren todos los radios en ángulos constantes y, por lo tanto, se ven como líneas que pasan por el centro. La imagen superior izquierda de la Figura \(\PageIndex{7}\) muestra dos nodos radiales, mientras que la imagen de la parte inferior derecha muestra el patrón de vibración asociado con tres nodos radiales y dos nodos angulares.

Figura \(\PageIndex{7}\): Las ondas estacionarias bidimensionales se pueden visualizar en una superficie vibrante. La superficie ha sido rociada con un polvo que se acumula cerca de las líneas nodales. Hay dos tipos de nodos visibles: nodos radiales (círculos) y nodos angulares (radios).Para un video más animado, use este enlace.

La Radiación del Cuerpo Negro y la Catástrofe Ultravioleta

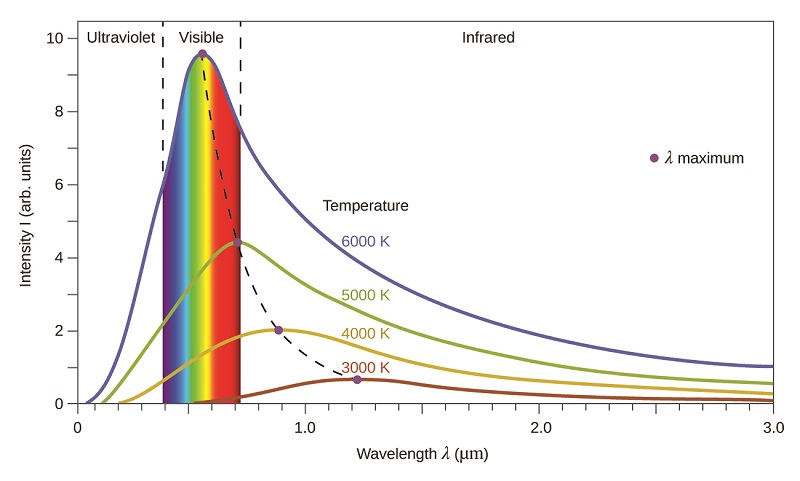
Las últimas décadas del siglo XIX fueron testigos de una intensa actividad de investigación en la comercialización de iluminación eléctrica recién descubierta. Esto requirió obtener una mejor comprensión de las distribuciones de luz emitidas desde varias fuentes consideradas. La iluminación artificial generalmente está diseñada para imitar la luz solar natural dentro de las limitaciones de la tecnología subyacente. Dicha iluminación consiste en un rango de frecuencias ampliamente distribuidas que forman un espectro continuo. La figura \(\PageIndex{8}\) muestra la distribución de longitud de onda para la luz solar. La radiación más intensa está en la región visible, con la intensidad disminuyendo rápidamente para luz ultravioleta (UV) de longitud de onda más corta, y más lentamente para luz infrarroja (IR) de longitud de onda más larga.

Figura \(\PageIndex{8}\): La distribución espectral (intensidad de la luz en función de la longitud de la onda) de la luz solar alcanza la atmósfera de la Tierra como luz UV, luz visible y luz IR. La luz solar no absorbida en la parte superior de la atmósfera tiene una distribución que coincide aproximadamente con la distribución teórica de un cuerpo negro a 5250 ° C, representada por la curva azul. (Crédito: modificación del trabajo de la Sociedad Americana para Pruebas y Materiales (ASTM) Espectros Terrestres de Referencia para la Evaluación del Desempeño Fotovoltaico)

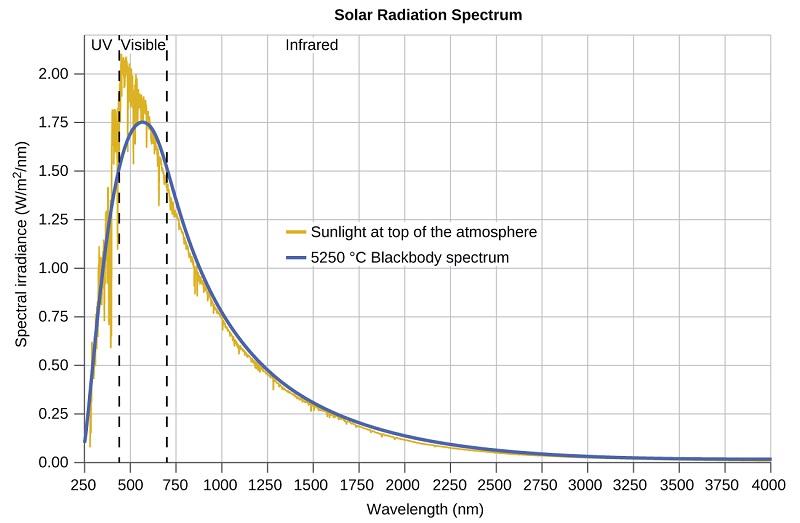
En la Figura \(\PageIndex{8}\), la distribución solar se compara con una distribución representativa, llamada el espectro de cuerpo negro, que corresponde a una temperatura de 5250°C. El espectro del cuerpo negro coincide bastante bien con el espectro solar. Un cuerpo negro es un emisor conveniente e ideal que se aproxima al comportamiento de muchos materiales cuando se calienta. Es "ideal" en el mismo sentido en que un gas ideal es una representación conveniente y simple de gases reales que funciona bien, siempre que la presión no sea demasiado alta ni la temperatura demasiado baja. Una buena aproximación de un cuerpo negro que se puede usar para observar la radiación del cuerpo negro es un horno de metal que se puede calentar a temperaturas muy altas. El horno tiene un pequeño orificio que permite observar la luz que se emite dentro del horno con un espectrómetro para poder medir las longitudes de onda y sus intensidades. La figura \(\PageIndex{8}\) muestra las curvas resultantes para algunas temperaturas representativas. Cada distribución depende solo de un único parámetro: la temperatura. Los máximos en las curvas del cuerpo negro, λ_max, cambian a longitudes de onda más cortas a medida que aumenta la temperatura, lo que refleja la observación de que los metales que se calientan a altas temperaturas comienzan a brillar de un rojo más oscuro que se vuelve más brillante a medida que aumenta la temperatura, y eventualmente se vuelve blanco caliente a temperaturas muy altas a medida que las intensidades de todas las longitudes de onda visibles se vuelven apreciables. Esta observación común estuvo en el corazón de la primera paradoja que mostró las limitaciones fundamentales de la física clásica que examinaremos.

Los físicos derivaron expresiones matemáticas para las curvas del cuerpo negro usando conceptos bien aceptados de las teorías de la mecánica clásica y el electromagnetismo clásico. Las expresiones teóricas como funciones de la temperatura se ajustan bien a las curvas experimentales experimentadas del cuerpo negro en longitudes de onda más largas, pero mostraron discrepancias significativas en longitudes de las ondas más cortas.Las curvas teóricas no solo no mostraron un pico, sino que mostraron absurdamente que la intensidad se hizo infinitamente grande a medida que la longitud de la onda se hacía más pequeña, lo que implicaría que los objetos cotidianos a temperatura ambiente deberían emitir grandes cantidades de luz UV. Esto se conoció como la "catástrofe ultravioleta" porque nadie pudo encontrar ningún problema con el tratamiento teórico que podría llevar a un comportamiento tan poco realista de onda corta. Finalmente, alrededor del 1900, Max Planck derivó una expresión teórica para la radiación del cuerpo negro que se ajusta exactamente a las observaciones experimentales (dentro del error experimental). Planck desarrolló su tratamiento teórico extendiendo el trabajo anterior que se había basado en la premisa de que los átomos que componían el horno vibraban a frecuencias crecientes (o longitudes de la onda decrecientes) a medida que la temperatura subía, siendo que estas vibraciones eran la fuente de la radiación electromagnética emitida. Pero donde los tratamientos anteriores permitieron que los átomos vibrantes tuvieran valores de energía obtenidos de un conjunto continuo de energías (perfectamente razonable, según la física clásica), Planck descubrió que al restringir las energías vibratorias a valores discretos para cada frecuencia, se podía derivar una expresión para la radiación del cuerpo negro que correctamente tuvo la intensidad disminuyendo rápidamente para las longitudes de onda cortas en la región UV.

\[E=nhν,\:n=1,2,3,\:. . .\]

La cantidad h es una constante que ahora se conoce como el constante de Planck, en su honor. Aunque Planck estaba satisfecho de haber resuelto la paradoja de la radiación del cuerpo negro, le molestaba que para hacerlo, tenía que asumir que los átomos vibrantes requerían energías cuantificadas, lo que no podía explicar. El valor del constante de Planck es muy pequeño, 6.626 × 10⁻³⁴ julios segundos (J s), lo que ayuda a explicar por qué la cuantificación de la energía no se había observado previamente en los fenómenos macroscópicos.

Figura \(\PageIndex{9}\): Se muestran curvas de distribución espectral del cuerpo negro para algunas temperaturas representativas.

El efecto fotoeléctrico

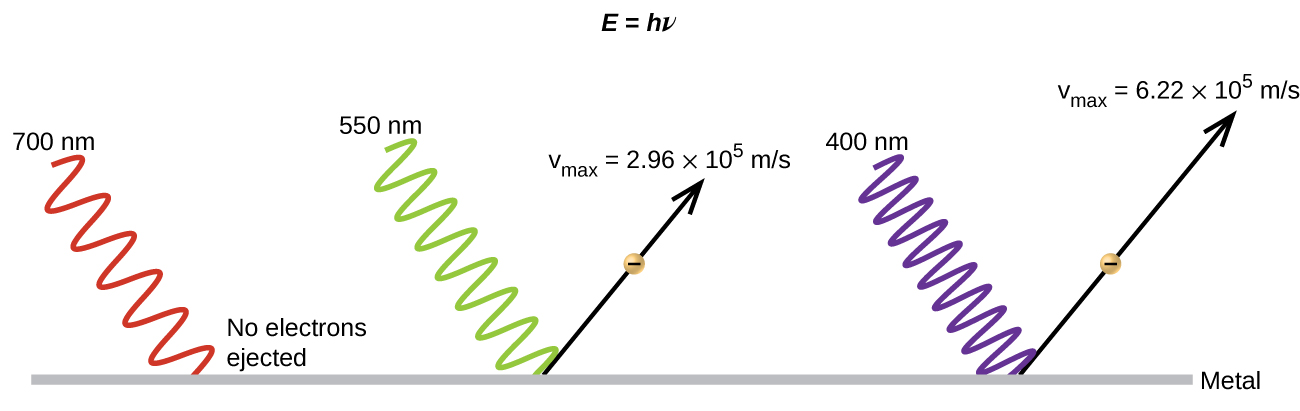
La siguiente paradoja en la teoría clásica por resolver se refiere al efecto fotoeléctrico (Figura \(\PageIndex{10}\)). Se había observado que los electrones podían ser expulsados de la superficie limpia de un metal cuando la luz que tenía una frecuencia mayor que la de una frecuencia umbral se reflejaba en ella. Sorprendentemente, la energía cinética de los electrones expulsados no dependía del brillo de la luz, sino que aumentaba a medida que aumentaba la frecuencia de la luz. Ya que los electrones en el metal tenían una cierta cantidad de energía de enlace manteniéndolos allí, la luz incidente necesitaba tener más energía para soltar los electrones. Según la teoría de la onda clásica, la energía de una onda depende de su intensidad (que depende de su amplitud), no de su frecuencia. Una parte de estas observaciones fue que la cantidad de electrones expulsados dentro de un período de tiempo determinado aumentaba a medida que aumentaba el brillo. En 1905, Albert Einstein pudo resolver la paradoja al incorporar los hallazgos de cuantización de Planck en la visión desacreditada de partículas de la luz (Einstein ganó su premio Nobel por este trabajo y no por sus teorías de la relatividad por las que es más famoso).

Einstein argumentó que las energías cuantificadas que Planck había postulado en su tratamiento de la radiación del cuerpo negro se podrían aplicar a la luz en el efecto fotoeléctrico, de modo que la luz que golpea la superficie del metal no se debería ver como una onda, sino como una corriente de partículas (luego llamados los fotones) cuya energía dependía de su frecuencia, de acuerdo con la fórmula de Planck, E = hν (o, en términos de longitud de onda usando c = νλ, \(E=\dfrac{hc}{λ}\)). Los electrones fueron expulsados ​​cuando fueron alcanzados por los fotones que tenían suficiente energía (una frecuencia mayor que el umbral). Lo más grande que sea la frecuencia, la energía cinética impartida será más grande que los electrones que escapan por las colisiones. Einstein también argumentó que la intensidad de la luz no dependía de la amplitud de la onda entrante, sino que correspondía al número de fotones que golpeaban la superficie dentro de un período de tiempo determinado. Esto explica por qué el número de electrones expulsados ​​aumentó con el aumento del brillo, ya que cuanto mayor es el número de fotones entrantes, mayor es la probabilidad de que colisionen con algunos de los electrones.

Con los hallazgos de Einstein, la naturaleza de la luz se hizo misterioso. Aunque muchos fenómenos de la luz se podrían explicar en términos de ondas o de partículas, ciertos fenómenos, como los patrones de interferencia obtenidos cuando la luz pasaba a través de una doble rendija, eran completamente contrarios a una vista de partículas de luz, mientras que otros fenómenos, como el Efecto Fotoeléctrico, eran completamente contrarios a una vista de onda de la luz. De alguna manera, en un nivel fundamental profundo que aún no se comprende, la luz es tanto ondulada como es partículas. Esto se conoce como dualidad onda-partícula.

Figura \(\PageIndex{10}\): Los fotones con bajas frecuencias no tienen suficiente energía para hacer que los electrones sean expulsados ​​a través del efecto fotoeléctrico. Para cualquier frecuencia de luz más grande que de la frecuencia umbral, la energía cinética de un electrón expulsado aumentará linealmente con la energía del fotón entrante.

Ejemplo \(\PageIndex{2}\): CALCULANDO LA ENERGÍA DE LA RADIACIÓN

Cuando vemos la luz de un signo de neón, estamos observando la radiación de los átomos de neón excitados. Si esta radiación tiene una longitud de onda de 640 nm, ¿Cuál es la energía del fotón que se está emitiendo?

Solución

Usamos la parte de la ecuación de Planck que incluye la longitud de la onda, λ, y convertimos las unidades de nanómetros en metros para que las unidades de λ y c sean iguales.

\[E=\dfrac{hc}{λ} \nonumber\]

\[\begin{align*}
E&=\mathrm{\dfrac{(6.626×10^{−34}\:J\cancel{s})(2.998×10^{8}\:m\cancel{s}^{−1})}{(640\cancel{nm})\left(\dfrac{1\:m}{10^9\cancel{nm}}\right)}}\\
E&=\mathrm{3.10×10^{−19}\:J}
\end{align*}\]

Ejercicio \(\PageIndex{2}\)

Los microondas en un horno son de una frecuencia específica que calentará las moléculas de agua contenidas en los alimentos. (Esta es la razón por la cual la mayoría de los plásticos y el vidrio no se calientan en un horno de microondas, no contienen moléculas de agua). Esta frecuencia es de aproximadamente 3 × 10⁹ Hz. ¿Cuál es la energía de un fotón en estos microondas?

Respuesta

2 × 10⁻²⁴ J

Ejemplo \(\PageIndex{3}\): El EFECTO FOTOELÉCTRICO

Identifique cuáles de las siguientes afirmaciones son falsas y, cuando sea necesario, cambie la palabra o frase en cursiva para que sean verdaderas, de acuerdo con la explicación de Einstein del efecto fotoeléctrico.

a. Aumentar el brillo de la luz entrante aumenta la energía cinética de los electrones expulsados.

b. Aumentar la longitud de la onda de la luz entrante aumenta la energía cinética de los electrones expulsados.

c. Aumentar el brillo de la luz entrante aumenta el número de electrones expulsados.

d. Aumentar la frecuencia de la luz entrante puede aumentar el número de electrones expulsados.

Solución

a. Falso. Aumentar el brillo de la luz entrante no tiene ningún efecto sobre la energía cinética de los electrones expulsados. Sólo la energía, no el número o la amplitud, de los fotones influye en la energía cinética de los electrones.

b. Falso. Aumentar la frecuencia de la luz entrante aumenta la energía cinética de los electrones expulsados. La frecuencia es proporcional a la energía e inversamente proporcional a la longitud de la onda. Las frecuencias más grandes que el valor umbral transfieren el exceso de energía a la energía cinética de los electrones.

c. Cierto. Debido a que la cantidad de colisiones con los fotones aumenta con una luz más brillante, la cantidad de electrones expulsados ​​aumenta.

d. Cierto con respecto al umbral de energía que une los electrones al metal. Por debajo de este umbral, los electrones no se emiten y por encima de ellos están. Una vez sobre el valor de umbral, aumentar la frecuencia no aumenta el número de electrones expulsados

Ejercicio \(\PageIndex{3}\)

Calcule el umbral de la energía en kJ/mol de electrones en aluminio, dado que el fotón de frecuencia más baja para el cual se observa el efecto fotoeléctrico es \(9.87 \times 10^{14}\; Hz\).

Respuesta

\(3.94 \: kJ/mol\)

Los espectros de línea

Otra paradoja dentro de la teoría electromagnética clásica con la que lucharon los científicos a fines del siglo XIX se refería a la luz emitida por los átomos y las moléculas. Cuando los sólidos, líquidos o los gases condensados ​​se calientan lo suficiente, irradian parte del exceso de energía en forma de luz. Los fotones producidos de esta manera tienen un rango de energías y, por lo tanto, producen un espectro continuo en el que está presente una serie ininterrumpida de las longitudes de la onda. La mayor parte de la luz generada por las estrellas (incluido nuestro sol) se produce de esta manera. Puede ver todas las longitudes de onda visibles de la luz presente en la luz solar usando un prisma para separarlas. Como se puede ver en la Figura 6.2.8, la luz solar también contiene luz UV (longitudes de onda más cortas) y luz IR (longitudes de onda más largas) que se pueden detectar usando instrumentos pero que son invisibles para el ojo humano. Los sólidos incandescentes (brillantes) como los filamentos de tungsteno en las luces incandescentes también emiten la luz que contiene todas las longitudes de onda de la luz visible. Estos espectros continuos a menudo se pueden aproximar mediante las curvas de radiación del cuerpo negro a una temperatura adecuada, como las que se muestran en Figura \(\PageIndex{9}\).

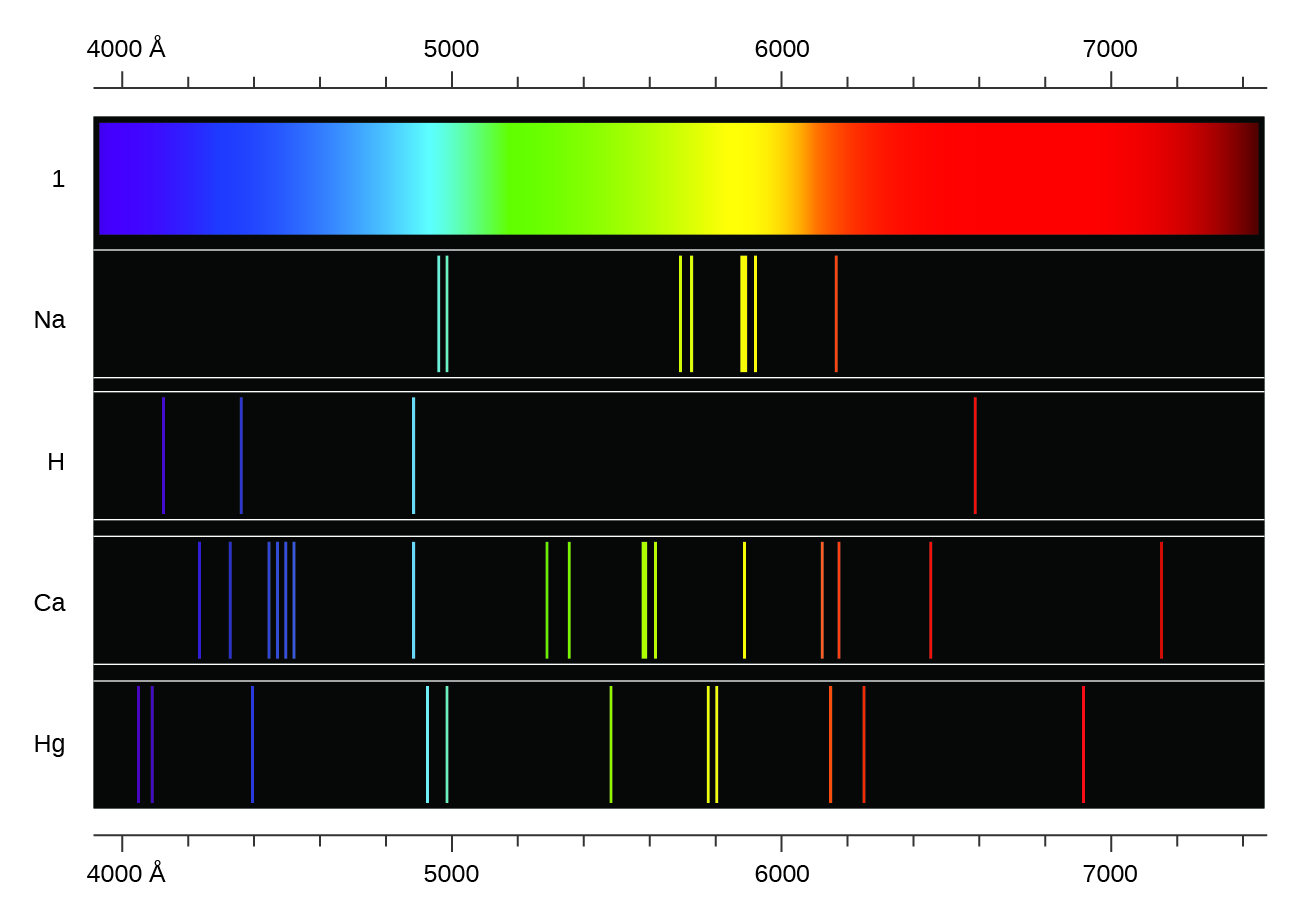
A diferencia de los espectros continuos, la luz también puede ocurrir como espectros discretos o lineales con anchos de línea muy estrechos intercalados en las regiones espectrales, como las que se muestran en la Figura \(\PageIndex{5}\). La activación de un gas a baja presión parcial con una corriente eléctrica, o su calentamiento, producirá espectros de línea. Las bombillas fluorescentes y los letreros de neón funcionan de esta manera (Figura \(\PageIndex{11}\)). Cada elemento muestra su propio conjunto característico de líneas, al igual que las moléculas, aunque sus espectros son generalmente mucho más complicados.

Figura \(\PageIndex{11}\): Los letreros de neón funcionan al excitar un gas a baja presión parcial usando una corriente eléctrica. Este signo muestra los efectos artísticos elaborados que se pueden lograr. (Crédito: Dave Shaver)

Cada línea de emisión consiste en una única longitud de la onda de luz, lo que implica que la luz emitida por un gas consiste en un conjunto de energías discretas. Por ejemplo, cuando una descarga eléctrica pasa a través de un tubo que contiene el gas hidrógeno a baja presión, las moléculas de H₂ se dividen en átomos de H separados, y vemos un color azul-rosado. Al pasar la luz a través de un prisma se produce un espectro de líneas, lo que indica que esta luz está compuesta por los fotones de cuatro longitudes de onda visibles, como se muestra en Figura \(\PageIndex{12}\).

Figura \(\PageIndex{12}\): Línea de espectros de gas selecto. Compare los dos tipos de espectros de emisión: espectro continuo de la luz blanca (arriba) y los espectros de línea de la luz de los átomos del sodio, el hidrógeno, el calcio y el mercurio excitados.

El origen de los espectros discretos en los átomos y las moléculas fue extremadamente desconcertante para los científicos a fines del siglo XIX, ya que, según la teoría electromagnética clásica, solo se deberían observar los espectros continuos. Aún más desconcertante, en 1885, Johann Balmer pudo derivar una ecuación empírica que relacionaba las cuatro longitudes de onda visibles de la luz emitida por los átomos del hidrógeno con números enteros. Esa ecuación es la siguiente, en la que k es una constante:

\[\dfrac{1}{λ}=k\left(\dfrac{1}{4}−\dfrac{1}{n^2}\right),\:n=3,\:4,\:5,\:6\]

Otras líneas discretas para el átomo del hidrógeno se encontraron en las regiones UV e IR. Johannes Rydberg generalizó el trabajo de Balmer y desarrolló una fórmula empírica que predijo todas las líneas de emisión de hidrógeno, no solo aquellas restringidas al rango visible, donde n₁ y n₂ son enteros, n₁<n₂, y \(R_∞\) es la constante de Rydberg (1.097 × 10⁷ m⁻¹).

\[\dfrac{1}{λ}=R_∞\left(\dfrac{1}{n^2_1}−\dfrac{1}{n^2_2}\right)\]

Incluso a fines del siglo XIX, la espectroscopia era una ciencia muy precisa, por lo que las longitudes de onda del hidrógeno se midieron con una precisión muy alta, lo que implicaba que el constante de Rydberg también se podía determinar con mucha precisión. Que una fórmula tan simple como la fórmula de Rydberg pudiera explicar mediciones tan precisas en aquel momento parecía sorprendente, pero fue la explicación final de los espectros de emisión de Neils Bohr en 1913 lo que finalmente convenció a los científicos a abandonar la física clásica y estimuló el desarrollo de la tecnología mecánica cuántica moderna.

Resumen

La luz y otras formas de radiación electromagnética se mueven a través del vacío con una velocidad constante, c, de 2.998 × 10⁸ m s^-1. Esta radiación muestra un comportamiento en forma de onda, que se puede caracterizar por una frecuencia, ν, y una longitud de onda, λ, tal que c = λν. La luz es un ejemplo de una onda viajera. Otros fenómenos de ondas importantes incluyen las ondas estacionarias, las oscilaciones periódicas y las vibraciones. Las ondas estacionarias exhiben cuantización, ya que sus longitudes de onda están limitadas a múltiplos enteros discretos de algunas longitudes características. La radiación electromagnética que pasa a través de dos rendijas estrechas separadas que tienen dimensiones aproximadamente similares a la longitud de la onda mostrará un patrón de interferencia que es el resultado de una interferencia constructiva y destructiva de las ondas. La radiación electromagnética también demuestra propiedades de las partículas llamadas los fotones. La energía de un fotón está relacionada con la frecuencia (o alternativamente, la longitud de la onda) de la radiación como E = hν (o \(E =\dfrac{hc}{λ}\)), donde h es la constante de Planck. Esa luz demuestra que tanto el comportamiento de la onda como el de la partícula se conoce como dualidad de onda-partícula. Todas las formas de radiación electromagnética comparten estas propiedades, aunque varias formas que incluyen rayos X, luz visible, microondas y ondas de radio interactúan de manera diferente con la materia y tienen aplicaciones prácticas muy diferentes. La radiación electromagnética se puede generar al excitar la materia a energías más altas, como al calentarla. La luz emitida puede ser continua (fuentes incandescentes como el sol) o discreta (de tipos específicos de átomos excitados). A menudo, los espectros continuos tienen distribuciones que se pueden aproximar a la radiación del cuerpo negro a una temperatura adecuada. El espectro lineal del hidrógeno se puede obtener pasando la luz desde un tubo electrificado de gas hidrógeno a través de un prisma. Este espectro de líneas era lo suficientemente simple como para que una fórmula empírica llamada fórmula de Rydberg pudiera derivarse del espectro. Tres paradojas históricamente importantes de fines del siglo XIX y principios del XX que no se pudieron explicar dentro del marco existente de la mecánica clásica y el electromagnetismo clásico fueron el problema del cuerpo negro, el efecto fotoeléctrico, y el espectro discreto de los átomos. La resolución de estas paradojas finalmente condujo a teorías cuánticas que reemplazaron a las teorías clásicas.

Ecuaciones claves

• c = λν
• \(E=hν=\dfrac{hc}{λ}\), where h = 6.626 × 10⁻³⁴ J s
• \(\dfrac{1}{λ}=R_∞\left(\dfrac{1}{n^2_1}−\dfrac{1}{n^2_2}\right)\)

Glosario

la amplitud

extensión del desplazamiento causado por una onda (para las ondas sinusoidales, es la mitad de la diferencia desde la altura del pico hasta la profundidad del canal, y la intensidad es proporcional al cuadrado de la amplitud).

cuerpo negro

Absorbente perfecto idealizado de toda radiación electromagnética incidente; tales cuerpos emiten radiación electromagnética en espectros continuos característicos llamados radiación de cuerpo negro.

espectro continuo

Radiación electromagnética emitida en una serie ininterrumpida de longitudes de onda (por ejemplo, luz blanca del sol).

la radiación electromagnética

La energía transmitida por ondas que tienen un componente de campo eléctrico y un componente de campo magnético.

el espectro electromagnético

El rango de energías que puede comprender la radiación electromagnética, que incluyen radio, microondas, infrarrojo, visible, ultravioleta, rayos X y rayos gamma; Como la energía de la radiación electromagnética es proporcional a la frecuencia e inversamente proporcional a la longitud de onda, el espectro también se puede especificar por rangos de frecuencias o longitudes de onda.

frecuencia (ν)

Número de ciclos de onda (picos o valles) que pasan un punto específico en el espacio por unidad de tiempo.

hertz (Hz)

la unidad de frecuencia, que es el número de ciclos por segundo, s ^-1

intensidad

La propiedad de la energía propagada por la onda relacionada con la amplitud de la onda, como el brillo de la luz o la intensidad del sonido

patron de interferencia

Patrón típicamente consistente en alternar franjas brillantes y oscuras; Es el resultado de la interferencia constructiva y destructiva de las ondas.

espectro de linea

La radiación electromagnética emitida en longitudes de onda discretas por un átomo específico (o átomos) en un estado excitado.

nodo

Cualquier punto de una onda estacionaria con amplitud cero.

fotón

El paquete más pequeño posible de radiación electromagnética, una partícula de luz.

cuantización

Ocurre solo en valores discretos específicos, no continuos.

onda estacionaria

Un fenómeno de onda localizado caracterizado por longitudes de ondas discretas determinadas por las condiciones de contorno utilizadas para generar las ondas; las ondas estacionarias son inherentemente cuantizadas.

onda

Oscilación que puede transportar energía de un punto a otro en el espacio.

longitud de onda (λ)

Distancia entre dos picos o valles consecutivos en una onda.

dualidad onda-partícula

El término usado para describir el hecho de que las partículas elementales, incluida la materia, presentan propiedades de ambas partículas (incluida la posición localizada, el momento) y las ondas (incluida la no localización, la longitud de onda y la frecuencia).

Contribuyentes

• {{Template.ContribOpenStaxSpanish()}

• Ana Martinez ([e-mail]) contribuyó a la traducción de este texto.