14.3: Fuerza relativa de los ácidos y las bases

Habilidades para desarrollar

• Explicar las siguientes leyes dentro de la Ley del Gas Ideal:
  • Ley de gases de Avogadro
• Evaluar las fuerzas relativas de los ácidos y las bases de acuerdo con sus constantes de ionización.
• Racionalizar las tendencias en la resistencia de ácido-base en relación con la estructura molecular
• Realizar cálculos de equilibrio para sistemas débiles de ácido-base.

Podemos clasificar las fuerzas de los ácidos según el grado en que se ionizan en una solución acuosa. La reacción de un ácido con el agua está dada por la expresión general:

\[\ce{HA}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{A-}(aq)\]

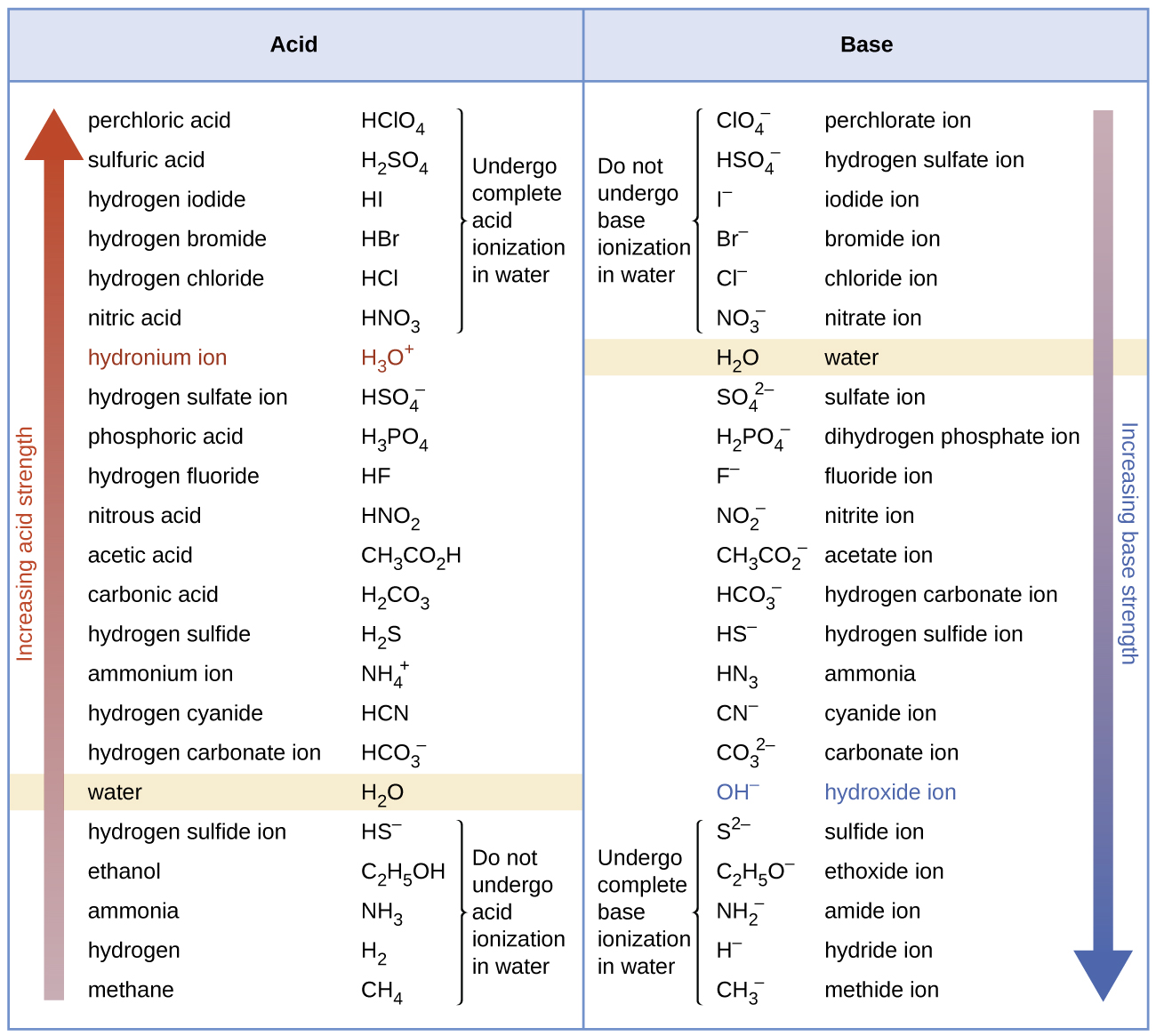
El agua es la base que reacciona con el ácido HA, A⁻ es la base conjugada del ácido HA y el ion de hidronio es el ácido conjugado del agua. Un ácido fuerte produce el 100% (o casi) de \(\ce{H3O+}\) y A⁻ cuando el ácido se ioniza en el agua; La Figura \(\PageIndex{1}\) enumera varios ácidos fuertes. Un ácido débil da pequeñas cantidades de \(\ce{H3O+}\) y \(A^-\).

Figura \(\PageIndex{1}\): Aquí se enumeran algunos de los ácidos y bases fuertes comunes.

Seis ácidos fuertes		Seis bases fuertes
\(\ce{HClO4}\)	ácido perclórico	\(\ce{LiOH}\)	hidróxido de litio
\(\ce{HCl}\)	ácido clorhídrico	\(\ce{NaOH}\)	hidróxido de sodio
\(\ce{HBr}\)	ácido bromhídrico	\(\ce{KOH}\)	hidróxido de potasio
\(\ce{HI}\)	ácido hidroyódico	\(\ce{Ca(OH)2}\)	hidróxido de calcio
\(\ce{HNO3}\)	ácido nítrico	\(\ce{Sr(OH)2}\)	hidróxido de estroncio
\(\ce{H2SO4}\)	ácido sulfúrico	\(\ce{Ba(OH)2}\)	hidróxido de bario

Las fuerzas relativas de los ácidos se pueden determinar midiendo sus constantes de equilibrio en soluciones acuosas. En soluciones de la misma concentración, los ácidos más fuertes se ionizan más y, por lo tanto, producen concentraciones más altas de iones de hidronio que los ácidos más débiles. La constante de equilibrio para un ácido se llama la constante de ionización ácida, K_a. Para la reacción de un ácido HA:

\[\ce{HA}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{A-}(aq)\]

Escribimos la ecuación para la constante de ionización como:

\[K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}}\]

donde las concentraciones son aquellas en equilibrio. Aunque el agua es un reactivo en la reacción, también es el disolvente, por lo que no incluimos [H₂O] en la ecuación. Cuanto más grande sea el valor de Ka de un ácido, más grande será la concentración de \(\ce{H3O+}\) y A⁻ en relación con la concentración del ácido no ionizado, HA. Por lo tanto, un ácido más fuerte tiene una constante de ionización más grande que un ácido más débil. Las constantes de ionización aumentan a medida que aumenta la fuerza del ácido.

Los siguientes datos sobre las constantes de ionización de los ácidos indican el orden de la concentración del ácido CH₃CO₂H < HNO₂ < \(\ce{HSO4-}\):

\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \hspace{20px} K_\ce{a}=1.8×10^{−5}\]

\[\ce{HNO2}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{NO2-}(aq) \hspace{20px} K_\ce{a}=4.6×10^{-4}\]

\[\ce{HSO4-}(aq)+\ce{H2O}(aq)⇌\ce{H3O+}(aq)+\ce{SO4^2-}(aq) \hspace{20px} K_\ce{a}=1.2×10^{−2}\]

Otra medida de la fuerza de un ácido es su porcentaje de ionización. El porcentaje de ionización de un ácido débil es la relación entre la concentración del ácido ionizado y la concentración del ácido inicial, multiplicado por 100:

\[\% \:\ce{ionization}=\ce{\dfrac{[H3O+]_{eq}}{[HA]_0}}×100\]

Debido a que la proporción incluye la concentración inicial, el porcentaje de ionización para una solución de un ácido débil dado varía según la concentración original del ácido, y en realidad disminuye al aumentar la concentración del ácido.

Ejemplo \(\PageIndex{1}\): Cálculo del porcentaje de ionización a partir del pH

Calcule el porcentaje de ionización de una solución 0.125-M de ácido nitroso (un ácido débil), con un pH de 2.09.

Solución

El porcentaje de ionización para un ácido es:

\[\ce{\dfrac{[H3O+]_{eq}}{[HNO2]_0}}×100 \nonumber \]

La ecuación química para la disociación del ácido nitroso es:

\[\ce{HNO2}(aq)+\ce{H2O}(l)⇌\ce{NO2-}(aq)+\ce{H3O+}(aq).\]

Ya que 10^−pH = \(\ce{[H3O+]}\), encontramos que 10^−2.09 = 8.1 × 10⁻³ M, entonces el porcentaje de ionización es:

\[\dfrac{8.1×10^{−3}}{0.125}×100=6.5\% \nonumber\]

Recuerde, el logaritmo 2.09 indica una concentración de iones de hidronio con solo dos cifras significativas.

Ejercicio \(\PageIndex{1}\)

Calcule el porcentaje de ionización de una solución 0.10-M de ácido acético con un pH de 2.89.

Respuesta

1.3% ionizado

Podemos clasificar la fuerza de las bases dependiendo de su tendencia a formar iones de hidróxido en una solución acuosa. La reacción de una base de Brønsted-Lowry con el agua se da por:

\[\ce{B}(aq)+\ce{H2O}(l)⇌\ce{HB+}(aq)+\ce{OH-}(aq)\]

El agua es un ácido que reacciona con una base \(\ce{HB^{+}}\) es el ácido conjugado de la base \(\ce{B}\), y el ion de hidróxido es la base conjugada del agua. Una base fuerte produce 100% (o casi) de OH^- y HB⁺ cuando reacciona con el agua; Figura \(\PageIndex{1}\) enumera varias bases fuertes. Una base débil produce una porción pequeña de iones de hidróxido. Los hidróxidos iónicos solubles como el NaOH se consideran bases fuertes porque se disocian completamente cuando se disuelven en el agua.

Como lo hicimos con los ácidos, podemos medir las fuerzas relativas de las bases cuando medimos su constante de ionización de bases (K_b) en soluciones acuosas. En soluciones de la misma concentración, las bases más fuertes se ionizan más y en consecuencia producen concentraciones más altas de iones de hidróxido que las bases más débiles. Una base más fuerte tiene una constante de ionización más grande que una base más débil. Para la reacción de una base, \(\ce{B}\):

\[\ce{B}(aq)+\ce{H2O}(l)⇌\ce{HB+}(aq)+\ce{OH-}(aq),\]

Escribimos la ecuación para la constante de ionización como:

\[K_\ce{b}=\ce{\dfrac{[HB+][OH- ]}{[B]}}\]

donde las concentraciones son aquellas en equilibrio. De nuevo no incluimos [H2O] en la ecuación porque el agua es el solvente. Las reacciones químicas y las constantes de ionización de las tres bases mostradas son

\[\ce{NO2-}(aq)+\ce{H2O}(l)⇌\ce{HNO2}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=2.17×10^{−11}\]

\[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=5.6×10^{−10}\]

\[\ce{NH3}(aq)+\ce{H2O}(l)⇌\ce{NH4+}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=1.8×10^{−5}\]

Una tabla de las constantes de ionización de las bases débiles se muestra en Tabla E2. Al igual que con los ácidos, el porcentaje de ionización se puede medir para las soluciones básicas, pero variará dependiendo de la constante de ionización de la base y la concentración inicial de la solución.

Considere las reacciones de ionización para un par de ácido-base conjugado, HA − A⁻:

\[\ce{HA}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{A-}(aq) \hspace{20px} K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}}\]

\[\ce{A-}(aq)+\ce{H2O}(l)⇌\ce{OH-}(aq)+\ce{HA}(aq) \hspace{20px} K_\ce{b}=\ce{\dfrac{[HA][OH]}{[A- ]}}\]

Al agregar estas dos ecuaciones químicas se obtiene la ecuación para la autoionización del agua:

\[\cancel{\ce{HA}(aq)}+\ce{H2O}(l)+\cancel{\ce{A-}(aq)}+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\cancel{\ce{A-}(aq)}+\ce{OH-}(aq)+\cancel{\ce{HA}(aq)}\]

\[\ce{2H2O}(l)⇌\ce{H3O+}(aq)+\ce{OH-}(aq)\]

Como se mostró en el capítulo anterior sobre el equilibrio, la expresión K para una ecuación química derivada por la adición de dos o más ecuaciones es el producto matemático de las expresiones K de las otras ecuaciones. La multiplicación de las expresiones de acción de masa y la cancelación de los términos comunes produce:

\[K_\ce{a}×K_\ce{b}=\ce{\dfrac{[H3O+][A- ]}{[HA]}×\dfrac{[HA][OH- ]}{[A- ]}}=\ce{[H3O+][OH- ]}=K_\ce{w}\]

Por ejemplo, la constante de ionización ácida del ácido acético (CH₃COOH) es 1.8 × 10⁻⁵, y la constante de ionización de la base de su base conjugada, el ion acetato \(\ce{(CH3COO-)}\), es 5.6 × 10^{− 10}) El producto de estos dos constantes es de hecho igual a K_w:

\[K_\ce{a}×K_\ce{b}=(1.8×10^{−5})×(5.6×10^{−10})=1.0×10^{−14}=K_\ce{w}\]

La medida en que un ácido, HA, dona sus protones a las moléculas de agua depende de la fuerza de la base conjugada, A^-, del ácido. Si A⁻ es una base fuerte, los protones que se donan a las moléculas de agua son recapturados por A⁻. Por lo tanto, hay relativamente poco de A⁻ y \(\ce{H3O+}\) en solución, y el ácido, HA, es débil. Si A⁻ es una base débil, el agua une los protones con más fuerza, y la solución contiene principalmente A⁻ y H₃O⁺: el ácido es fuerte. Los ácidos fuertes forman bases conjugadas muy débiles, y los ácidos débiles forman bases conjugadas más fuertes (Figura \(\PageIndex{2}\)).

Figura \(\PageIndex{2}\): Este diagrama muestra las fuerzas relativas de los pares de ácido-base conjugados, como lo indican sus constantes de ionización en una solución acuosa.

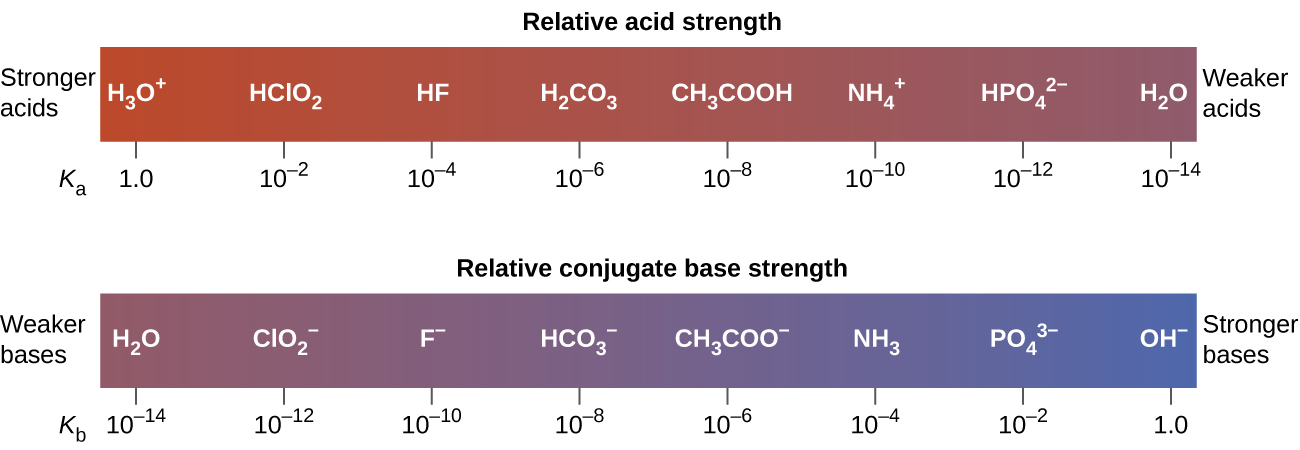
Figura \(\PageIndex{3}\) enumera una serie de ácidos y bases en el orden de las resistencias decrecientes de los ácidos y las resistencias crecientes correspondientes de las bases. El ácido y la base en una fila dada son conjugadas el uno al otro.

Figura \(\PageIndex{3}\): El gráfico muestra las fuerzas relativas de los pares ácido-base conjugados.

Los primeros seis ácidos en la Figura \(\PageIndex{3}\) son los ácidos fuertes más comunes. Estos ácidos están completamente disociados en una solución acuosa. Las bases conjugadas de estos ácidos son bases más débiles que el agua. Cuando uno de estos ácidos se disuelve en el agua, sus protones se transfieren completamente al agua que es la base más fuerte.

Los ácidos que se encuentran entre el ion de hidronio y el agua en la Figura \(\PageIndex{3}\) forman bases conjugadas que pueden competir con el agua por la posesión de un protón. Tanto los iones de hidronio como las moléculas de ácido no ionizado están presentes en equilibrio en una solución de uno de estos ácidos. Los compuestos que son ácidos más débiles que el agua (los que se encuentran debajo del agua en la columna de los ácidos) en la Figura \(\PageIndex{3}\) no exhiben un comportamiento de ácido observable cuando se disuelven en el agua. Sus bases conjugadas son más fuertes que el ion de hidróxido, y si se formara alguna base conjugada, reaccionaría con el agua para volver a formar el ácido.

La medida en que una base forma de iones hidróxido en solución acuosa depende de la fuerza de la base con respecto a la del ión de hidróxido, como se muestra en la última columna de la Figura \(\PageIndex{3}\). Una base fuerte, como una de las que se encuentran debajo del ion de hidróxido, acepta protones del agua para producir el 100% del ácido conjugado y el ion de hidróxido. Esas bases que se encuentran entre el agua y el ion de hidróxido aceptan protones del agua, pero resulta una mezcla del ion de hidróxido y la base. Las bases que son más débiles que el agua (las que se encuentran por encima del agua en la columna de bases) no demuestran un comportamiento básico observable en una solución acuosa.

Ejemplo \(\PageIndex{2}\): El producto de K_a × K_b = K_w

Use el K_b para el ion de nitrito, \(\ce{NO2-}\), para calcular el K_a para su ácido conjugado.

Solución

K_b para \(\ce{NO2-}\) se da en esta sección como 2.17×10^−11. El ácido conjugado de \(\ce{NO2-}\) es HNO₂; el K_a para HNO₂ puede ser calculado usando la relación:

\[K_\ce{a}×K_\ce{b}=1.0×10^{−14}=K_\ce{w} \nonumber\]

Resolviendo para K_a, obtenemos:

\[K_\ce{a}=\dfrac{K_\ce{w}}{K_\ce{b}}=\dfrac{1.0×10^{−14}}{2.17×10^{−11}}=4.6×10^{−4} \nonumber\]

Esta respuesta se puede verificar encontrando el K_a para HNO₂ en la Table E1

Ejercicio \(\PageIndex{2}\)

Podemos determinar las fuerzas relativas de los ácidos \(\ce{NH4+}\) y HCN comparando sus constantes de ionización. La constante de ionización de HCN se da en la Tabla E1 como 4.9×10⁻¹⁰. La constante de ionización de \(\ce{NH4+}\) no se da, pero la constante de ionización de su base conjugada, NH₃, se da como 1.8×10⁻⁵. Determine la constante de ionización de \(\ce{NH4+}\) y decida cuál es el ácido más fuerte, HCN o \(\ce{NH4+}\).

Respuesta

\(\ce{NH4+}\) es el ácido un poco mas fuerte (K_a for \(\ce{NH4+}\) = 5.6 × 10⁻¹⁰).

La ionización de los ácidos y bases débiles

Varios ácidos y bases son débiles; es decir, no se ionizan completamente en soluciones acuosas. Una solución de un ácido débil en agua es una mezcla del ácido no ionizado, el ion de hidronio, y la base conjugada del ácido, con el ácido no ionizado presente en la concentración más grande. En consecuencia, un ácido débil aumenta la concentración de ion de hidronio en una solución acuosa (pero no tanto como la misma cantidad de un ácido fuerte).

El ácido acético, CH₃CO₂H, es un ácido débil. Cuando agregamos ácido acético al agua, se ioniza un poco de acuerdo con esta ecuación:

\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq)\]

dando una mezcla de equilibrio con la mayor parte del ácido presente en la forma no ionizada (molecular). Este equilibrio, como otros equilibrios, es dinámico; las moléculas del ácido acético donan iones de hidrógeno a las moléculas de agua y forman iones de hidronio e iones de acetato al mismo tiempo que los iones de hidronio donan iones de hidrógeno a iones de acetato para reformar las moléculas de ácido acético y las moléculas de agua. Podemos ver que cuando medimos el pH de una solución acuosa de concentración conocida que solo una fracción del ácido débil se ioniza en cualquier momento (Figura \(\PageIndex{4}\)). El ácido débil restante está presente en la forma no ionizada.

Para el ácido acético en equilibrio

\[K_\ce{a}=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}}=1.8 \times 10^{−5}\]

Figura \(\PageIndex{4}\): El papel de pH indica que una solución de HCl 0.l-M (vaso de precipitados a la izquierda) tiene un pH de 1. El ácido está completamente ionizado y \(\ce{[H3O+]}\) = 0.1 M. Una solución de CH3CO2H 0.1-M (vaso de precipitados a la derecha) tiene un pH de 3 (\(\ce{[H3O+]}\) = 0.001 M) porque el ácido débil CH3CO2H está solo parcialmente ionizado. En esta solución, \(\ce{[H3O+]}\)<[CH3CO2H]. (crédito: modificación del trabajo de Sahar Atwa)

Tabla \(\PageIndex{1}\): Constantes de ionización de algunos ácidos débiles

Reacción de ionización	Ka a 25 °C
\(\ce{HSO4- + H2O ⇌ H3O+ + SO4^2-}\)	1.2 × 10^−2
\(\ce{HF + H2O ⇌ H3O+ + F-}\)	3.5 × 10^−4
\(\ce{HNO2 + H2O ⇌ H3O+ + NO2-}\)	4.6 × 10^−4
\(\ce{HNCO + H2O ⇌ H3O+ + NCO-}\)	2 × 10^−4
\(\ce{HCO2H + H2O ⇌ H3O+ + HCO2-}\)	1.8 × 10^−4
\(\ce{CH3CO2H + H2O ⇌ H3O+ + CH3CO2-}\)	1.8 × 10^−5
\(\ce{HCIO + H2O ⇌ H3O+ + CIO-}\)	2.9 × 10^−8
\(\ce{HBrO + H2O ⇌ H3O+ + BrO-}\)	2.8 × 10^−9
\(\ce{HCN + H2O ⇌ H3O+ + CN-}\)	4.9 × 10^−10

Tabla \(\PageIndex{1}\) nos da las constantes de ionización para varios ácidos débiles; las constantes de ionización adicionales se pueden encontrar en Tabla E1.

En equilibrio, una solución de una base débil en el agua es una mezcla de la base no ionizada, el ácido conjugado de la base débil y el ion hidróxido con la base no ionizada presente en la mayor concentración. Por lo tanto, una base débil aumenta la concentración de iones hidróxido en una solución acuosa (pero no tanto como la misma cantidad de una base fuerte).

Por ejemplo, una solución de la base débil trimetilamina, (CH₃)₃N, en el agua reacciona de acuerdo con la ecuación:

\[\ce{(CH3)3N}(aq)+\ce{H2O}(l)⇌\ce{(CH3)3NH+}(aq)+\ce{OH-}(aq)\]

Esto proporciona una mezcla de equilibrio con la mayor parte de la base presente como la amina no ionizada. Este equilibrio es análogo al equilibrio descrito para los ácidos débiles.

Podemos confirmar midiendo el pH de una solución acuosa de una base débil de concentración conocida que solo una fracción de la base reacciona con el agua (Figura 14.4.5). La base débil restante está presente como la forma sin reaccionar. La constante de equilibrio para la ionización de una base débil, K_b, se llama la constante de ionización de la base débil, y es igual al cociente de reacción cuando la reacción está en equilibrio. Para trimetilamina, en equilibrio:

\[K_\ce{b}=\ce{\dfrac{[(CH3)3NH+][OH- ]}{[(CH3)3N]}}\]

Figura \(\PageIndex{5}\): El papel de pH indica que una solución 0.1-M de NH₃ (izquierda) es un poco básica. La solución tiene un pOH de 3 ([OH−] = 0.001 M) porque la base débil NH₃ solo reacciona parcialmente con el agua. Una solución de NaOH 0.1-M (derecha) tiene un pOH de 1 porque NaOH es una base fuerte. (crédito: modificación del trabajo de Sahar Atwa)

Las constantes de ionización de varios bases débiles se dan en la Tabla \(\PageIndex{2}\) y en Tabla E2.

Tabla\(\PageIndex{2}\): Las constantes de ionización de algunos bases débiles

Reacción de ionización	Kb a 25 °C
\(\ce{(CH3)2NH + H2O ⇌ (CH3)2NH2+ + OH-}\)	5.9 × 10^−4
\(\ce{CH3NH2 + H2O ⇌ CH3NH3+ + OH-}\)	4.4 × 10^−4
\(\ce{(CH3)3N + H2O ⇌ (CH3)3NH+ + OH-}\)	6.3 × 10^−5
\(\ce{NH3 + H2O ⇌ NH4+ + OH-}\)	1.8 × 10^−5
\(\ce{C6H5NH2 + H2O ⇌ C6N5NH3+ + OH-}\)	4.3 × 10^−10

Ejemplo \(\PageIndex{3}\): Determinación de K_a a partir de las concentraciones a equilibrio

El ácido acético es el ingrediente principal del vinagre; por eso sabe agrio. En equilibrio, una solución contiene [CH₃CO₂H] = 0.0787 M y \(\ce{[H3O+]}=\ce{[CH3CO2- ]}=0.00118\:M\). ¿Cuál es el valor de K_a para el ácido acético?

El vinagre es una solución de ácido acético, un ácido débil. (crédito: modificación del trabajo por "HomeSpot HQ" / Flickr)

Solución

Debemos calcular la constante de equilibrio a partir de las concentraciones de equilibrio. En equilibrio, el valor de la constante de equilibrio es igual al cociente de reacción para la reacción:

\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \nonumber\]

\[K_\ce{a}=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}}=\dfrac{(0.00118)(0.00118)}{0.0787}=1.77×10^{−5} \nonumber\]

Ejercicio \(\PageIndex{3}\)

Cuál es la constante de equilibrio para la ionización del ion \(\ce{HSO4-}\), el ácido débil que se utiliza en algunos limpiadores domésticos.

\[\ce{HSO4-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{SO4^2-}(aq) \nonumber\]

En una mezcla de NaHSO₄ y Na₂SO₄ a equilibrio, \(\ce{[H3O+]}\) = 0.027 M; \(\ce{[HSO4- ]}=0.29\:M\); y \(\ce{[SO4^2- ]}=0.13\:M\).

Respuesta

\(K_a\) de \(\ce{HSO_4^-}= 1.2 ×\times 10^{−2}\)

Ejemplo \(\PageIndex{4}\): Determinación de K_b a partir de las concentraciones a equilibrio

La cafeina, C₈H₁₀N₄O₂ es una base débil. ¿Cual es el valor de K_b de la cafeina si una solución de cafeina a equilibrio tiene [C₈H₁₀N₄O₂] = 0.050 M, \(\ce{[C8H10N4O2H+]}\) = 5.0 × 10⁻³ M, y [OH⁻] = 2.5 × 10⁻³ M?

Solución

En equilibrio, el valor de la constante de equilibrio es igual al cociente de reacción para la reacción:

\[\ce{C8H10N4O2}(aq)+\ce{H2O}(l)⇌\ce{C8H10N4O2H+}(aq)+\ce{OH-}(aq) \nonumber\]

\[K_\ce{b}=\ce{\dfrac{[C8H10N4O2H+][OH- ]}{[C8H10N4O2]}}=\dfrac{(5.0×10^{−3})(2.5×10^{−3})}{0.050}=2.5×10^{−4} \nonumber\]

Ejercicio \(\PageIndex{4}\)

Cuál es la constante de equilibrio para la ionización del ion \(\ce{HPO4^2-}\), una base débil.

\[\ce{HPO4^2-}(aq)+\ce{H2O}(l)⇌\ce{H2PO4-}(aq)+\ce{OH-}(aq) \nonumber\]

Una solución que contiene una mezcla de NaH₂PO₄ y Na₂HPO₄ a equilibrio, [OH⁻] = 1.3 × 10⁻⁶ M; \(\ce{[H2PO4- ]}=0.042\:M\) ; y \(\ce{[HPO4^2- ]}=0.341\:M\).

Respuesta

K_b de \(\ce{HPO4^2-}=1.6×10^{−7} \nonumber\)

Ejemplo \(\PageIndex{5}\): Determinación de K_a o K_b a partir de pH

El pH de una solución de 0.0516-M ácido nitroso, HNO₂ es 2.34. ¿Cuál es el K_a del ácido?

\[\ce{HNO2}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{NO2-}(aq) \nonumber\]

Solución

Determinamos una constante de equilibrio comenzando con las concentraciones iniciales de HNO₂, \(\ce{H3O+}\) y \(\ce{NO2-}\), así como una de las concentraciones finales, la concentración del ion hidronio en el equilibrio. (Recuerde que el pH es simplemente otra forma de expresar la concentración del ion hidronio).

Podemos resolver este problema con los siguientes pasos en los que x es un cambio en la concentración de una especie en la reacción

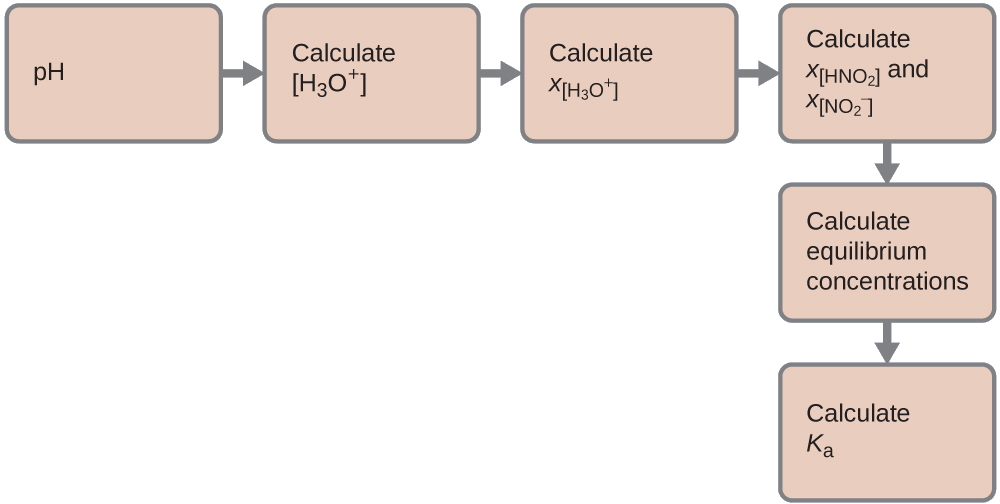
Podemos resumir las diversas concentraciones y cambios como se muestra aquí (la concentración del agua no aparece en la expresión de la constante de equilibrio, por eso no necesitamos considerar su concentración):

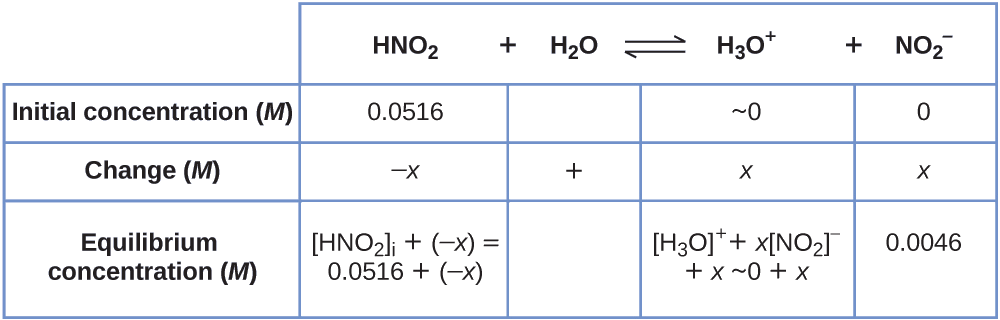
Para obtener los varios valores en la tabla ICE (Inicial, Cambio, Equilibrio), primero calculamos \(\ce{[H3O+]}\), la concentración de equilibrio de \(\ce{H3O+}\), a partir del pH:

\[\ce{[H3O+]}=10^{−2.34}=0.0046\:M \nonumber\]

El cambio en la concentración de \(\ce{H3O+}\), \(x_{\ce{[H3O+]}}\), es la diferencia entre la concentración de equilibrio de H₃O⁺, que determinamos a partir del pH, y el valor de la concentración inicial, \(\mathrm{[H_3O^+] _ i}\). La concentración inicial de \(\ce{H3O+}\) es su concentración en el agua pura, que es mucho menor que la concentración final que la aproximamos a cero (~ 0).

El cambio en la concentración de \(\ce{NO2-}\) es igual al cambio en la concentración de \(\ce{[H3O+]}\). Por cada 1 mol de \(\ce{H3O+}\) que se forma, se forma 1 mol de \(\ce{NO2-}\). La concentración de equilibrio de HNO₂ es igual a su concentración inicial más el cambio en su concentración.

Ahora podemos completar la tabla ICE con las concentraciones en equilibrio, como se muestra aquí:

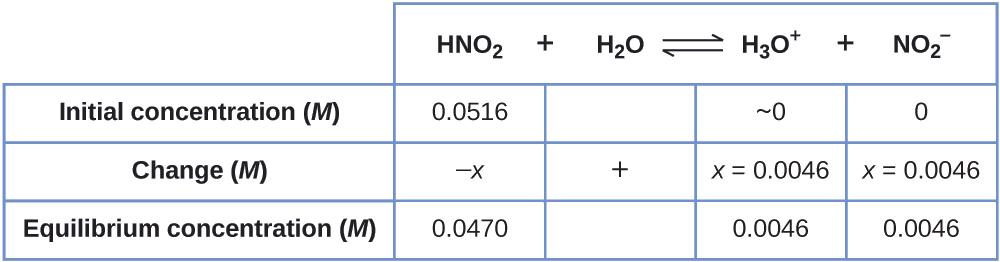
Finalmente, calculamos el valor de la constante de equilibrio utilizando los datos de la tabla:

\[K_\ce{a}=\ce{\dfrac{[H3O+][NO2- ]}{[HNO2]}}=\dfrac{(0.0046)(0.0046)}{(0.0470)}=4.5×10^{−4} \nonumber\]

Ejercicio \(\PageIndex{5}\)

El pH de una solución de amoníaco doméstico, una solución de NH₃ 0.950-M, es 11.612. ¿Cuál es el K_b para NH₃?

Respuesta

\(K_b = 1.8 × 10^{−5}\)

Ejemplo \(\PageIndex{6}\): Concentraciones de equilibrio en una solución de un ácido débil

El ácido fórmico, HCO₂H, es el irritante que causa la reacción del cuerpo a las picaduras de hormigas.

El dolor de la picadura de una hormiga es causada por el ácido fórmico. (crédito: John Tann)

¿Cuál es la concentración de los iones hidronio y el pH en una solución de ácido fórmico 0.534-M?

\[\ce{HCO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HCO2-}(aq) \hspace{20px} K_\ce{a}=1.8×10^{−4} \nonumber\]

Solución

1. Determine x y las concentraciones de equilibrio. La expresión de equilibrio es:

\[\ce{HCO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HCO2-}(aq) \nonumber\]

La concentración del agua no aparece en la expresión de la constante de equilibrio, por eso no debemos considerar su cambio de concentración al configurar la tabla de ICE.

La tabla muestra las concentraciones iniciales (concentraciones antes de que el ácido se ioniza), los cambios en la concentración y las concentraciones de equilibrio que siguen (los datos dados en el problema aparecen en color):

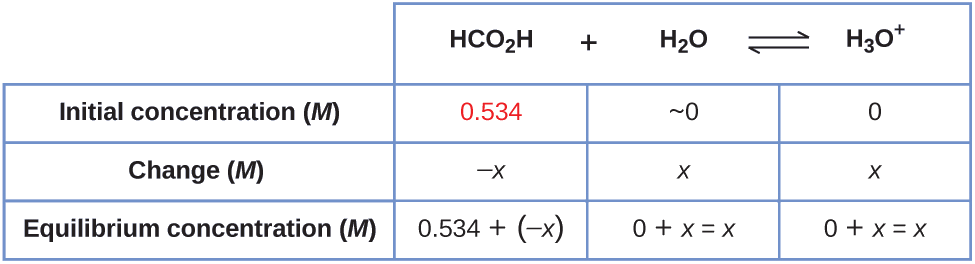
2. Resuelva para x y las concentraciones de equilibrio. En equilibrio:

\[\begin{align*} K_\ce{a} &=1.8×10^{−4}=\ce{\dfrac{[H3O+][HCO2- ]}{[HCO2H]}} \\[5pt] &=\dfrac{(x)(x)}{0.534−x}=1.8×10^{−4} \end{align*}\]

Ahora resuelva para x. Debido a que la concentración inicial del ácido es razonablemente grande y la constante K_a es muy pequeña, asumimos que x << 0.534, lo que nos permite simplificar el término del denominador como (0.534 - x) = 0.534. Esto da:

\[K_\ce{a}=1.8×10^{−4}=\dfrac{x^{2}}{0.534} \nonumber\]

Resuelva para x de la siguiente manera:

\[ x^2 =0.534×(1.8×10^{−4}) =9.6×10^{−5} \\[5pt] x =\sqrt{9.6×10^{−5}} \\[5pt] =9.8×10^{−3} \]

Para verificar la suposición de que \(x\) es pequeño en comparación con 0.534, calculamos:

\[\begin{align*} \dfrac{x}{0.534} &=\dfrac{9.8×10^{−3}}{0.534} \\[5pt] &=1.8×10^{−2} \, \textrm{(1.8% of 0.534)} \end{align*}\]

x es menos del 5% de la concentración inicial, la suposición es válida.

Encontramos la concentración de equilibrio del ion hidronio en esta solución de ácido fórmico a partir de su concentración inicial y el cambio en esa concentración como se indica en la última línea de la tabla:

\[\begin{align*} \ce{[H3O+]} &=~0+x=0+9.8×10^{−3}\:M. \\[5pt] &=9.8×10^{−3}\:M \end{align*}\]

El pH de la solución se puede encontrar tomando el logaritmo negativo de \(\ce{[H3O+]}\), entonces:

\(pH = −\log(9.8×10^{−3})=2.01\)

Ejercicio \(\PageIndex{6}\)

Solo una pequeña fracción de un ácido débil se ioniza en una solución acuosa. ¿Cuál es el porcentaje de ionización del ácido acético en una solución de ácido acético 0.100-M CH₃CO₂H?

\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \hspace{20px} K_\ce{a}=1.8×10^{−5} \nonumber\]

(Sugerencia: Determine \(\ce{[CH3CO2-]}\) a equilibrio.) Recuerde que el porcentaje de ionización es la fracción del ácido acético ionizado × 100, o \(\ce{\dfrac{[CH3CO2- ]}{[CH3CO2H]_{initial}}}×100\).

Respuesta

porcentaje de ionización = 1.3%

Los siguientes ejemplos muestran que la concentración de los productos producidos por la ionización de una base débil se pueden determinar mediante la misma serie de pasos utilizados para un ácido débil.

Ejemplo \(\PageIndex{7}\): Concentraciones de equilibrio en una solución de una base débil

Determine la concentración del ion de hidróxido en una solución de 0.25-M de trimetilamina, una base débil.

\[\ce{(CH3)3N}(aq)+\ce{H2O}(l)⇌\ce{(CH3)3NH+}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=6.3×10^{−5} \nonumber\]

Solución

Este problema requiere que calculemos una concentración de equilibrio determinando los cambios de concentración a medida que la ionización de una base va hacia el equilibrio. La solución se aborda de la misma manera que para la ionización del ácido fórmico en el Ejemplo \(\PageIndex{6}\). Los reactivos y los productos serán diferentes y los números serán diferentes, pero la lógica será la misma:

1. Determine x y las concentraciones de equilibrio. La tabla muestra los cambios y las concentraciones:

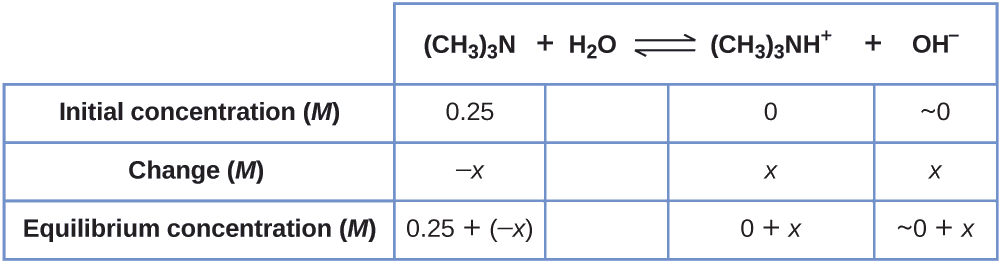
2. Resuelve para x y las concentraciones de equilibrio. En equilibrio:

\[K_\ce{b}=\ce{\dfrac{[(CH3)3NH+][OH- ]}{[(CH3)3N]}}=\dfrac{(x)(x)}{0.25−x=}6.3×10^{−5} \nonumber\]

Si suponemos que x es pequeño en relación con 0.25, entonces podemos reemplazar (0.25 - x) en la ecuación anterior con 0.25. Resolver la ecuación simplificada nos da:

\[x=4.0×10^{−3} \nonumber\]

Este cambio es menos de 5% de la concentración inicial (0.25), por eso esta suposición es justa.

Recuerde que, para este cálculo, x es igual a la concentración de equilibrio del ion hidróxido en la solución (vea la tabulación anterior):

\[(\ce{[OH- ]}=~0+x=x=4.0×10^{−3}\:M \nonumber\]

\[=4.0×10^{−3}\:M \nonumber\]

Luego, calcule el pOH en la siguiente manera:

\[\ce{pOH}=−\log(4.3×10^{−3})=2.40 \nonumber\]

Usando la relación introducida en la sección anterior de este capítulo:

\[\mathrm{pH + pOH=p\mathit{K}_w=14.00} \nonumber\]

permite el cálculo del pH:

\[\mathrm{pH=14.00−pOH=14.00−2.37=11.60} \nonumber\]

Revise el trabajo. Una comprobación de nuestra aritmética muestra que K_b = 6.3 × 10⁻⁵.

Ejercicio \(\PageIndex{7}\)

1. Muestre que el cálculo en el Paso 2 de este ejemplo da una x de 4.3 × 10⁻³ y el cálculo en el Paso 3 muestra Kb = 6.3 × 10⁻⁵.
2. Encuentre la concentración de ion hidróxido en una solución de amoníaco 0.0325-M, una base débil con un Kb de 1.76 × 10⁻⁵. Calcule el porcentaje de ionización de amoníaco, la fracción ionizada × 100, o \(\ce{\dfrac{[NH4+]}{[NH3]}}×100\)

Respuesta a

\(7.56 × 10^{−4}\, M\), 2.33%

Respuesta b

2.33%

Algunos ácidos y bases débiles se ionizan de tal manera que la suposición simplificadora de que x es pequeña en relación con la concentración inicial del ácido o la base es inapropiada. A medida que resolvemos para las concentraciones de equilibrio en tales casos, veremos que no podemos descuidar el cambio en la concentración inicial del ácido o la base, y debemos resolver las ecuaciones de equilibrio utilizando la ecuación cuadrática.

Ejemplo \(\PageIndex{8}\): Concentraciones de equilibrio en una solución de un ácido débil

El bisulfato de sodio, NaHSO₄, se usa en algunos limpiadores domésticos porque contiene el ion \(\ce{HSO4-}\), un ácido débil. ¿Cuál es el pH de una solución de 0.50-M de \(\ce{HSO4-}\)?

\[\ce{HSO4-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{SO4^2-}(aq) \hspace{20px} K_\ce{a}=1.2×10^{−2} \nonumber\]

Solución

Necesitamos determinar la concentración de equilibrio del ion hidronio que resulta de la ionización de \(\ce{HSO4-}\) para que podamos usar \(\ce{[H3O+]}\) para determinar el pH. Como en los ejemplos anteriores, podemos abordar la solución mediante los siguientes pasos:

1. Determine x y las concentraciones de equilibrio. Esta tabla muestra los cambios y las concentraciones:

2. Resuelva para x y las concentraciones

A medida que comenzamos a resolver para x, encontraremos que esto es más complicado que en los ejemplos anteriores. Mientras discutimos estas complicaciones, no debemos perder de vista el hecho de que todavía es el propósito de este paso determinar el valor de x.

A equilibrio:

\[K_\ce{a}=1.2×10^{−2}=\ce{\dfrac{[H3O+][SO4^2- ]}{[HSO4- ]}}=\dfrac{(x)(x)}{0.50−x} \nonumber\]

Si suponemos que x es pequeño y aproximado (0.50 - x) como 0.50, encontramos:

\[x=7.7×10^{−2} \nonumber\]

Cuando verificamos la suposición, confirmamos:

\[\dfrac{x}{\mathrm{[HSO_4^- ]_i}} \overset{?}{\le} 0.05 \nonumber\]

que para este sistema es

\[\dfrac{x}{0.50}=\dfrac{7.7×10^{−2}}{0.50}=0.15(15\%) \nonumber\]

El valor de \(x\) no es menos de 5% de 0.50, por eso la suposición no es válida. Necesitamos la fórmula cuadrática para encontrar \(x\).

La ecuación:

\[K_\ce{a}=1.2×10^{−2}=\dfrac{(x)(x)}{0.50−x} \nonumber\]

nos da

\[6.0×10^{−3}−1.2×10^{−2}x=x^{2+} \nonumber\]

o

\[x^{2+}+1.2×10^{−2}x−6.0×10^{−3}=0\ \nonumber\]

Esta ecuación se puede resolver usando la fórmula cuadrática. Para una ecuación de la forma

\[ax^{2+} + bx + c=0, \nonumber\]

x se da por la ecuación:

\[x=\dfrac{−b±\sqrt{b^{2+}−4ac}}{2a} \nonumber\]

En este problema, a = 1, b = 1.2 × 10⁻³, y c = −6.0 × 10⁻³.

Resolver para x da una raíz negativa (que no puede ser correcta ya que la concentración no puede ser negativa) y una raíz positiva:

\[x=7.2×10^{−2} \nonumber\]

Ahora determine la concentración de iones hidronio y el pH:

\[\ce{[H3O+]}=~0+x=0+7.2×10^{−2}\:M \nonumber\]

\[=7.2×10^{−2}\:M\]

El pH de esta solución es:

\[\mathrm{pH=−log[H_3O^+]=−log7.2×10^{−2}=1.14} \nonumber\]

Ejercicio \(\PageIndex{8}\)

1. Demuestre que la fórmula cuadrática nos da \(x = 7.2 × 10^{−2}\).
2. Calcule el pH de una soluciona de 0.010-M cafeína, una base débil.

\[\ce{C8H10N4O2}(aq)+\ce{H2O}(l)⇌\ce{C8H10N4O2H+}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=2.5×10^{−4} \nonumber\]

Sugerencia

Será necesario convertir [OH⁻] a \(\ce{[H3O+]}\) o pOH a pH hacia el final del cálculo.

Respuesta

pH 11.16

Las fortalezas relativas de los ácidos y las bases fuertes

Los ácidos fuertes, como HCl, HBr y HI, todos exhiben la misma fuerza en el agua. La molécula de agua es una base tan fuerte en comparación con las bases conjugadas Cl^-, Br⁻ e I^- que la ionización de estos ácidos fuertes es esencialmente completa en soluciones acuosas. En solventes menos básicos que el agua, vemos que HCl, HBr y HI difieren notablemente en su tendencia a ceder un protón al solvente. Por ejemplo, cuando se disuelve en el etanol (una base más débil que el agua), el grado de ionización aumenta en el siguiente orden HCl <HBr <HI, por lo que se demuestra que HI es el ácido más fuerte de estos ácidos. La incapacidad para discernir las diferencias de fuerza entre los ácidos fuertes disueltos en el agua se conoce como el efecto nivelador del agua.

El agua también ejerce un efecto nivelador sobre las fortalezas de las bases fuertes. Por ejemplo, el ion óxido, O₂⁻, y el ion amida, \(\ce{NH2-}\), son bases tan fuertes que reaccionan completamente con el agua:

\[\ce{O^2-}(aq)+\ce{H2O}(l)⟶\ce{OH-}(aq)+\ce{OH-}(aq)\]

\[\ce{NH2-}(aq)+\ce{H2O}(l)⟶\ce{NH3}(aq)+\ce{OH-}(aq)\]

En consecuencia, O₂⁻ y \(\ce{NH2-}\) parecen tener la misma fuerza de base en el agua; ambos dan un rendimiento del 100% de ion hidróxido.

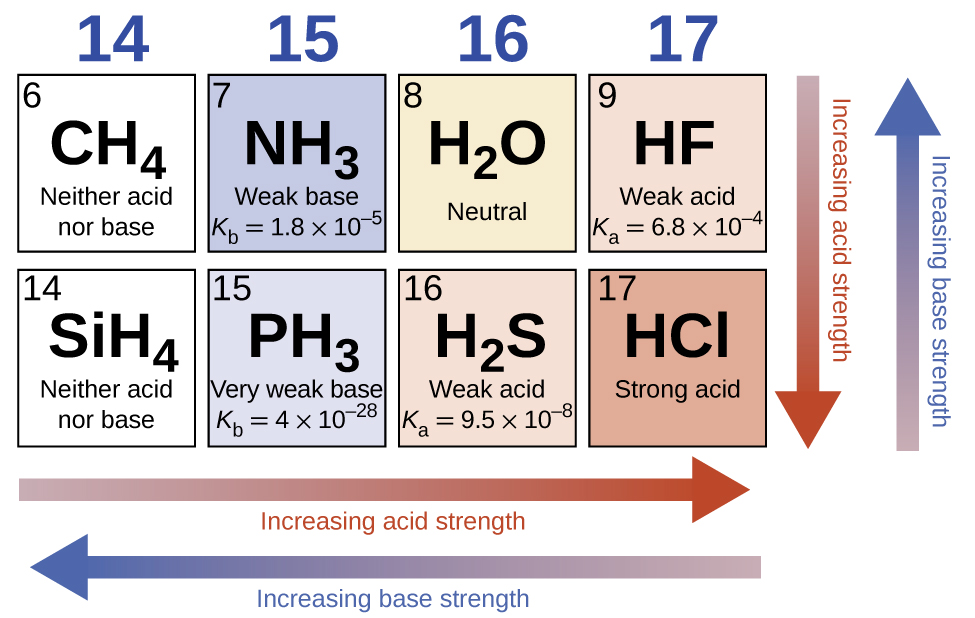
En ausencia de cualquier efecto de nivelación, la fuerza ácida de los compuestos binarios de hidrógeno con no metales (A) aumenta a medida que la fuerza del enlace H-A disminuye un grupo en la tabla periódica. Para el grupo 17, el orden de acidez creciente es HF <HCl <HBr <HI. Del mismo modo, para el grupo 16, el orden de aumento de la fuerza del ácido es H₂O <H₂S <H₂Se <H₂Te. A lo largo de una fila en la tabla periódica, la fuerza ácida de los compuestos de hidrógeno binarios aumenta al aumentar la electronegatividad del átomo no metálico porque aumenta la polaridad del enlace H-A. Por lo tanto, el orden de acidez creciente (para la eliminación de un protón) a través de la segunda fila es CH₄ <NH₃ <H₂O <HF; en la tercera fila, es SiH₄ <PH₃ <H₂S <HCl (vea Figura \(\PageIndex{6}\)).

Figura \(\PageIndex{6}\): A medida que se mueva de izquierda a derecha y hacia abajo en la tabla periódica, la fuerza del ácido aumenta. A medida que se mueva de derecha a izquierda y hacia arriba, la fuerza de la base aumenta.

Los compuestos que contienen el oxígeno y uno o mas grupos hidroxilos (OH) pueden ser acídicos, básicos, o anfótero, dependiendo de la posición del átomo central (E) en la tabla periódica, el átomo unido al grupo hidroxilo. Dichos compuestos tienen la fórmula general O_nE(OH)_m, y incluyen el ácido sulfúrico, O₂S(OH)₂, el ácido sulfuroso, OS(OH)₂, el ácido nítrico, O₂NOH, el ácido perclórico, O₃ClOH, el hidróxido de aluminio, Al(OH)₃, el hidróxido de calcio, Ca(OH)₂ e el hidróxido de potasio, KOH:

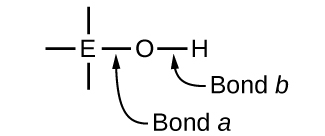
Si el átomo central, E, tiene una baja electronegatividad, su atracción para los electrones es baja. Existe poca tendencia para que el átomo central forme un enlace covalente fuerte con el átomo de oxígeno, y el enlace a entre el elemento y el oxígeno se rompe más fácilmente que el enlace b entre el oxígeno y el hidrógeno. Por lo tanto, el enlace a es iónico, los iones de hidróxido se liberan a la solución y el material se comporta como una base; este es el caso con Ca(OH)₂ y KOH. La baja electronegatividad es característica de los elementos más metálicos, por eso los elementos metálicos forman hidróxidos iónicos que son, por definición, compuestos básicos.

Si, por otro lado, el átomo E tiene una electronegatividad relativamente alta, atrae fuertemente los electrones que comparte con el átomo de oxígeno, lo que hace que el enlace sea relativamente covalente. El enlace oxígeno-hidrógeno, enlace b, se debilita porque los electrones se desplazan hacia E. El enlace b es polar y libera los iones de hidrógeno fácilmente a la solución, por lo que el material se comporta como un ácido. Las altas electronegatividades son características de los elementos más no metálicos. Por lo tanto, los elementos no metálicos forman compuestos covalentes que contienen grupos ácidos -OH que se llaman oxiácidos.

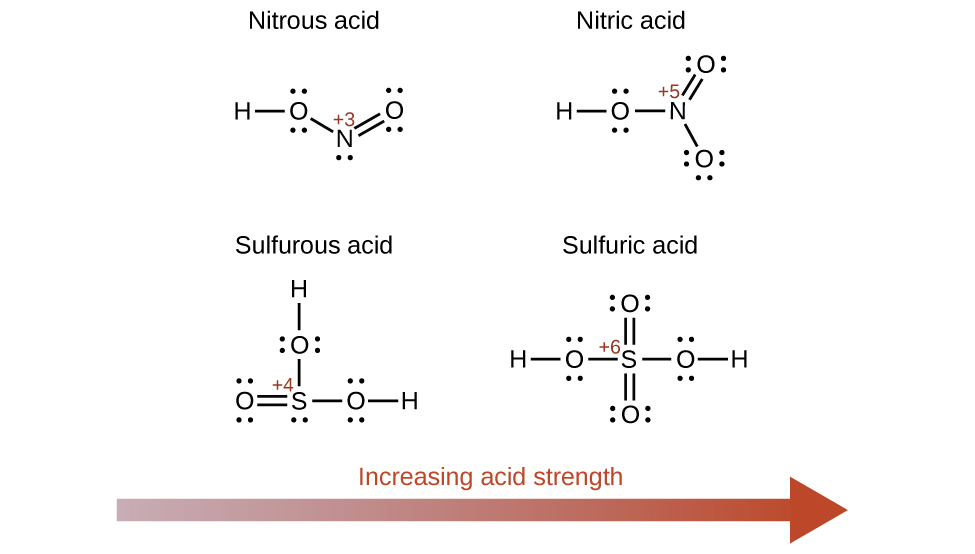
Aumentar el número de oxidación del átomo central E también aumenta la acidez de un oxácido porque esto aumenta la atracción de E por los electrones que comparte con el oxígeno y, por lo tanto, debilita el enlace O-H. El ácido sulfúrico, H₂SO₄ o O₂S(OH)₂ (con un número de oxidación de azufre de +6), es más acídico que el ácido sulfuroso, H₂SO₃ o OS(OH)₂ (con un número de oxidación de azufre de +4). Del mismo modo, el ácido nítrico, HNO₃ o O₂NOH (número de oxidación N = +5), es más acídico que el ácido nitroso, HNO₂ o ONOH (número de oxidación N = +3). En cada uno de estos pares, el número de oxidación del átomo central es mayor para el ácido más fuerte (Figura \(\PageIndex{7}\)).

Figura \(\PageIndex{7}\): A medida que el número de oxidación del átomo central E aumenta, la acidez también aumenta.

Los compuestos hidroxilados de los elementos con electronegatividades intermedias y números de oxidación relativamente altos (por ejemplo, los elementos cerca de la línea diagonal que separa los metales de los no metales en la tabla periódica) son usualmente anfóteros. Esto significa que los compuestos hidroxilados actúan como ácidos cuando reaccionan con las bases fuertes y como bases cuando reaccionan con los ácidos fuertes. El anfoterismo del hidróxido de aluminio, que comúnmente existe como el hidrato Al(H2O)3(OH)3, se refleja en su solubilidad tanto en los ácidos fuertes como en las bases fuertes. En bases fuertes, el hidróxido de aluminio hidratado relativamente insoluble, Al(H2O)3(OH)3, se convierte en el ion soluble, \(\ce{[Al(H2O)2(OH)4]-}\), cuando reacciona con el ion hidróxido:

\[[\ce{Al(H2O)3(OH)3}(aq)+\ce{OH-}(aq)⇌\ce{H2O}(l)+\ce{[Al(H2O)2(OH)4]-}(aq)\]

En esta reacción, se transfiere un protón desde una de las moléculas de H2O unidas por el aluminio a un ion hidróxido en solución. El compuesto Al(H2O)3(OH)3 actúa así como un ácido en estas condiciones. Por otro lado, cuando se disuelve en los ácidos fuertes, se convierte en el ion soluble \(\ce{[Al(H2O)6]^3+}\) reacciona con el ion hidronio:

\[\ce{3H3O+}(aq)+\ce{Al(H2O)3(OH)3}(aq)⇌\ce{Al(H2O)6^3+}(aq)+\ce{3H2O}(l)\]

En este caso, los protones se transfieren desde los iones hidronio en solución hacia Al(H₂O)₃(OH)₃, y el compuesto funcional como una base.

Resumen

Las concentraciones de los ácidos y las bases de Brønsted-Lowry en soluciones acuosas se pueden determinar por sus constantes de ionización de ácido o base. Los ácidos más fuertes forman bases conjugadas más débiles, y los ácidos más débiles forman bases conjugadas más fuertes. Por lo tanto, los ácidos fuertes están completamente ionizados en solución acuosa porque sus bases conjugadas son bases más débiles que el agua. Los ácidos débiles están solo parcialmente ionizados porque sus bases conjugadas son lo suficientemente fuertes como para competir exitosamente con el agua por la posesión de protones. Las bases fuertes reaccionan con el agua para cuantitativamente formar iones de hidróxido. Las bases débiles dan solo pequeñas cantidades de ion hidróxido. Las fuerzas de los ácidos binarios aumentan de izquierda a derecha a lo largo de un período de la tabla periódica (CH₄ <NH₃ <H₂O <HF), y aumentan en un grupo (HF <HCl <HBr <HI). Las fortalezas de los oxiácidos que contienen el mismo elemento central aumentan a medida que aumenta el número de oxidación del elemento (H₂SO₃ <H₂SO₄). Las fortalezas de los oxiácidos también aumentan a medida que aumenta la electronegatividad del elemento central [H₂SeO₄ <H₂SO₄].

Ecuaciones Clave

• \(K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}}\)
• \(K_\ce{b}=\ce{\dfrac{[HB+][OH- ]}{[B]}}\)
• \(K_a \times K_b = 1.0 \times 10^{−14} = K_w \,(\text{at room temperature})\)
• \(\textrm{Percent ionization}=\ce{\dfrac{[H3O+]_{eq}}{[HA]_0}}×100\)

Glosario

constante de ionización ácida (K_a)

constante de equilibrio para la ionización de un ácido dé

constante de ionización base (K_b)

constante de equilibrio para la ionización de una base débil

efecto nivelador del agua

cualquier ácido más fuerte que \(\ce{H3O+}\), o cualquier base más fuerte que OH− reaccionará con el agua para formar \(\ce{H3O+}\), o OH−, respectivamente; el agua actúa como una base para hacer que todos los ácidos fuertes parezcan igualmente fuertes, y actúa como un ácido para hacer que todas las bases fuertes parezcan igualmente fuertes

oxiácido

compuesto que contiene un grupo no metálico y uno o más grupos hidroxilo

porcentaje de ionización

relación de la concentración del ácido ionizado a la concentración de ácido inicial, multiplicado por 100

Contribuyentes

• Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."

• Ana Martinez ([e-mail]) contribuyó a la traducción de este texto.