19.3: Propiedades ópticas y magnéticas de los compuestos de coordinación
- Page ID
- 1968
Habilidades para desarrollar
- Resumir la premisa básica de la teoría del campo cristalino (CFT)
- Identificar las geometrías moleculares asociadas con varios patrones de división d-orbital
- Predecir las configuraciones electrónicas de orbitales d divididos para átomos o iones de metales de transición seleccionados
- Explicar las propiedades espectrales y magnéticas en términos de conceptos CFT
El comportamiento de los compuestos de coordinación no se puede explicar adecuadamente con las mismas teorías usadas para la química de los elementos del grupo principal. Las geometrías observadas de los complejos de coordinación no son consistentes con los orbitales hibridados en el metal central que se superponen con los orbitales del ligando, como lo predeciría la teoría del enlace de valencia. Los colores observados indican que los orbitales d a veces ocurren en diferentes niveles de energía en lugar de ser todos degenerados, es decir, de igual energía, como son los tres orbitales p. Para explicar las estabilidades, estructuras, colores y propiedades magnéticas de los complejos de metales de transición, se ha desarrollado un modelo de unión diferente. Así como la teoría del enlace de valencia explica muchos aspectos del enlace en la química del grupo principal, la teoría del campo cristalino es útil para comprender y predecir el comportamiento de los complejos de los metales de transición.
La teoría del campo cristalino
Para explicar el comportamiento observado de los complejos de metales de transición (por ejemplo, cómo resultan los colores), se ha desarrollado un modelo que involucra las interacciones electrostáticas entre los electrones de los ligandos y los electrones en los orbitales d no hibridados del átomo metálico central. Este modelo electrostático es la teoría del campo cristalino (CFT). Nos permite comprender, interpretar y predecir los colores, el comportamiento magnético y algunas estructuras de los compuestos de coordinación de los metales de transición.
CFT se enfoca en los electrones no enlazantes del ion metálico central en los complejos de coordinación, no en los enlaces de metal-ligando. Igual a la teoría del enlace de valencia, CFT cuenta solo una parte de la historia del comportamiento de los complejos. Sin embargo, le dice lo que la teoría del enlace de valencia no le dice. En su forma pura, CFT ignora cualquier enlace covalente entre ligandos e iones metálicos. Tanto el ligando como el metal se tratan como cargas puntuales infinitesimalmente pequeñas.
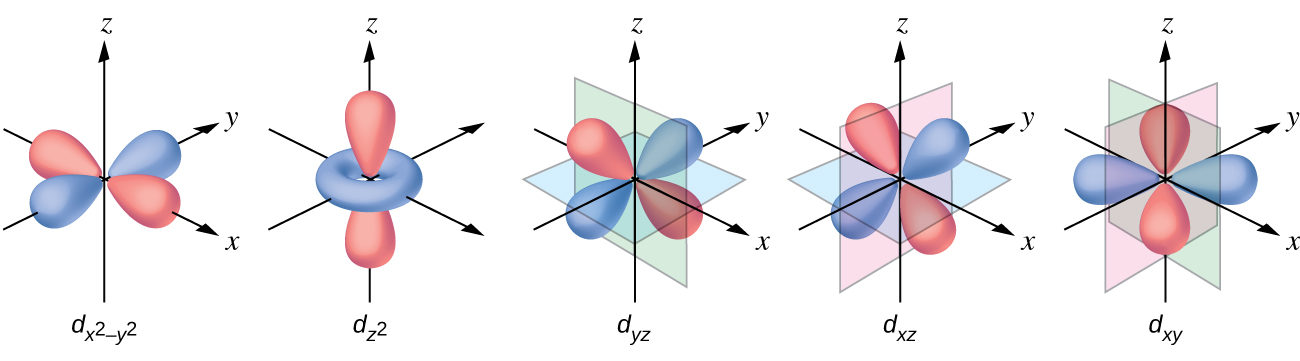
Todos los electrones son negativos, por eso los electrones donados por los ligandos repelerán los electrones del metal central. Consideremos el comportamiento de los electrones en los orbitales d sin hibridar en un complejo octaédrico. Los cinco orbitales d consisten en regiones con forma de lóbulo y están dispuestos en el espacio, como se muestra en la Figura \(\PageIndex{1}\). En un complejo octaédrico, los seis ligandos se coordinan a lo largo de los ejes.
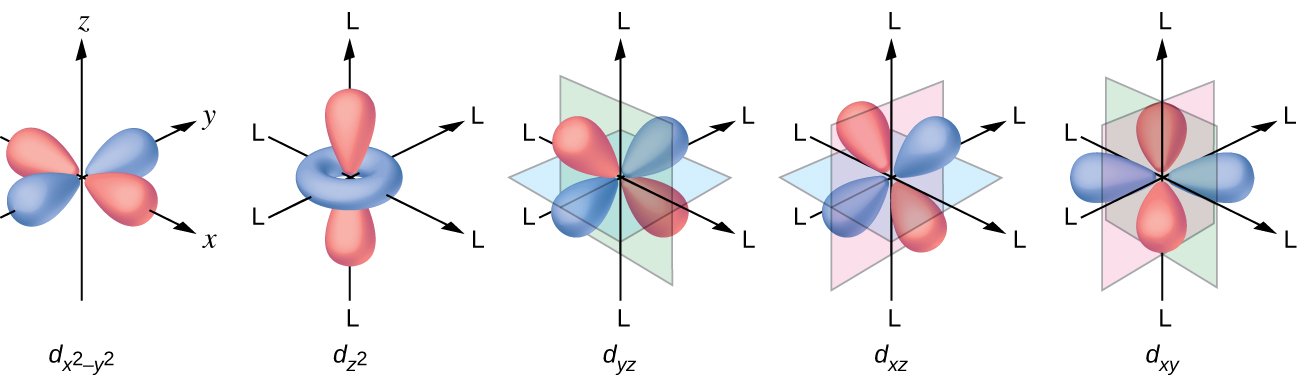
Figura \(\PageIndex{1}\): Aquí se muestran las características direccionales de los cinco orbitales d. Las porciones sombreadas indican la fase de los orbitales. Los ligandos (L) se coordinan a lo largo de los ejes. Para mayor claridad, los ligandos se han omitido del orbital \(d_{x^2−y^2}\) para que se puedan mostrar las etiquetas de los ejes.
En un ion metálico sin complejos en la fase gaseosa, los electrones se distribuyen entre los cinco orbitales d de acuerdo con la regla de Hund porque todos los orbitales tienen la misma energía. Sin embargo, cuando los ligandos se coordinan con un ion metálico, las energías de los orbitales d ya no son iguales.
En los complejos octaédricos, los lóbulos de dos de los cinco orbitales d, los orbitales \(d_{z^2}\) y \(d_{x^2−y^2}\), apuntan hacia los ligandos (Figura \(\PageIndex{1}\)). Estos dos orbitales se llaman orbitales eg (el símbolo en realidad se refiere a la simetría de los orbitales, pero lo usaremos como un nombre conveniente para estos dos orbitales en un complejo octaédrico). Los otros tres orbitales, los orbitales dxy, dxz y dyz, tienen lóbulos que apuntan entre los ligandos y se llaman los orbitales t2g (nuevamente, el símbolo realmente se refiere a la simetría de los orbitales). Cuando seis ligandos se acercan al ion metálico a lo largo de los ejes del octaedro, sus cargas puntuales repelen los electrones en los orbitales d del ion metálico. Sin embargo, las repulsiones entre los electrones en los orbitales eg (Los orbitales \(d_{z^2}\) y \(d_{x^2−y^2}\)) y los ligandos son mayores que las repulsiones entre los electrones en los orbitales t2g (los orbitales dzy, dxz y dyz) y los ligandos. Esto se debe a que los lóbulos de los orbitales eg apuntan directamente a los ligandos, mientras que los lóbulos de los orbitales t2g apuntan entre ellos. Así, los electrones en los orbitales eg del ion metálico en un complejo octaédrico tienen energías potenciales más altas que las de los electrones en los orbitales t2g. La diferencia de energía se puede representar como se muestra en la Figura \(\PageIndex{2}\).
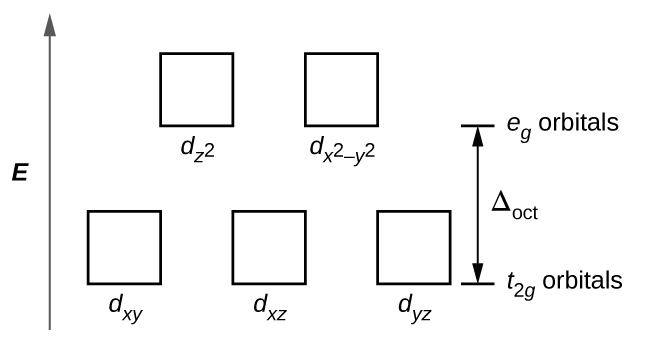
Figura \(\PageIndex{2}\): En los complejos octaédricos, los orbitales eg están desestabilizados (con mayor energía) en comparación con los orbitales t2g porque los ligandos interactúan más fuertemente con los orbitales d que están apuntando directamente.
La diferencia de energía entre los orbitales eg y t2g se llama una división del campo de cristal y está simbolizada por Δoct, donde oct significa octaédrico.
La magnitud de Δoct depende de muchos factores, incluida la caracteristica de los seis ligandos ubicados alrededor del ión metálico central, la carga en el metal y si el metal usa orbitales 3d, 4d o 5d. Los diferentes ligandos producen diferentes divisiones del campo de cristal. La creciente división del campo cristalino producida por los ligandos se expresa en la serie espectroquímica, una versión corta de la cual se da aquí:
\[\large \underset{\textrm{a few ligands of the spectrochemical series, in order of increasing field strength of the ligand}}{\xrightarrow{\ce{I- <Br- <Cl- <F- <H2O<C2O4^2- <NH3<\mathit{en}<NO2- <CN-}}}\]
En esta serie, los ligandos de la izquierda provocan pequeñas divisiones del campo de cristal y son ligandos de campo débil, mientras que los de la derecha provocan divisiones más grandes y son ligandos de campo fuerte. Por lo tanto, el valor de Δoct para un complejo octaédrico con ligandos de yoduro (I-) es mucho menor que el valor de Δoct para el mismo metal con ligandos de cianuro (CN-).
Los electrones en los orbitales d siguen el principio de aufbau ("llenan"), que dice que los orbitales se llenarán para dar la energía total más baja, al igual que en la química del grupo principal. Cuando dos electrones ocupan el mismo orbital, las cargas similares se repelen entre sí. La energía necesaria para emparejar dos electrones en un solo orbital se llama la energía de emparejamiento (P). Los electrones siempre ocuparán individualmente cada orbital en un conjunto degenerado antes de emparejarse. P es similar en magnitud a Δoct. Cuando los electrones llenan los orbitales d, las magnitudes relativas de Δoct y P determinan qué orbitales estarán ocupados.
En [Fe(CN)6]4−, el campo fuerte de seis ligandos de cianuro produce un Δoct grande. En estas condiciones, los electrones requieren menos energía para emparejarse que requieren para excitarse a los orbitales eg (Δoct> P). Los seis electrones 3d del par de iones Fe2+ en los tres orbitales t2g (Figura \(\PageIndex{3}\)). Los complejos en los que los electrones están emparejados debido a la gran división del campo cristalino se llaman los complejos de bajo espín porque se minimiza el número de electrones no emparejados (espines).
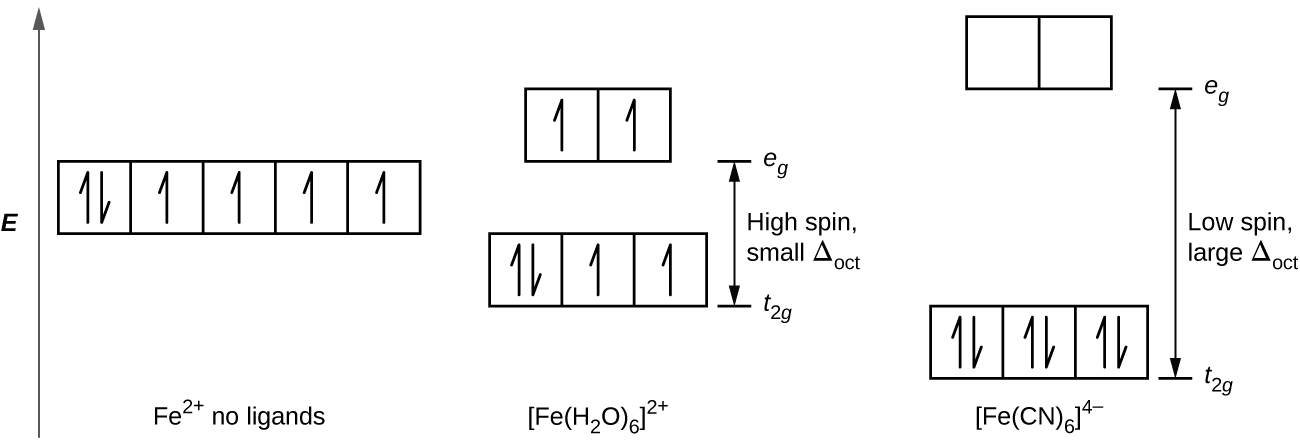
Figura \(\PageIndex{3}\): Los complejos de hierro (II) tienen seis electrones en los orbitales 5d. En la ausencia de un campo cristalino, los orbitales están degenerados. Para complejos de coordinación con ligandos de campo fuertes como [Fe(CN)6]4−, Δoct es mayor que P, y los electrones se emparejan en los orbitales t2g de menor energía antes de ocupar los orbitales, eg. En los ligandos de campo débil como H2O, la división del campo del ligando es menor que la energía de apareamiento, Δoct menor que P, por eso los electrones ocupan todos los orbitales d individualmente antes de que ocurra cualquier apareamiento.
En [Fe(H2O)6]2+, por otro lado, el campo débil de las moléculas de agua produce sólo una pequeña división del campo cristalino (Δoct <P). Debido a que se requiere menos energía para que los electrones ocupen los orbitales eg que para emparejarse, habrá un electrón en cada uno de los cinco orbitales 3d antes de que se emparejen. Para los seis d electrones en el centro del hierro (II) en [Fe(H2O)6]2+, habrá un par de electrones y cuatro electrones no apareados (Figura \(\PageIndex{3}\)). Los complejos como el ion [Fe(H2O)6]2+, en el que los electrones no están emparejados porque la división del campo cristalino no es lo suficientemente grande como para hacer que se emparejen, se llaman los complejos de alto espín porque el número de electrones desapareados (espines) se maximiza.
Un proceso de pensamiento similar muestra por qué el ion [Fe(CN)6]3− es un complejo de espín bajo con un solo electrón desapareado, mientras que los iones [Fe(H2O)6]3+ y [FeF6]3− son complejos de alto espín con cinco electrones desapareados.
Ejemplo \(\PageIndex{1}\): Los complejos de alta y baja espín
Prediga la cantidad de electrones desapareados
- K3[CrI6]
- [Cu(en)2(H2O)2]Cl2
- Na3[Co(NO2)6]
Solución
Los complejos son octaédricos.
- Cr3+ tiene una configuracion d 3. Estos electrones no estarán emparejados.
- Cu2+ es d 9, por eso habrá un electrón desapareado.
- Co3+ tiene electrones de valencia d 6, por eso la división del campo de cristal determinará cuántos electrones están emparejados. El nitrito es un ligando de campo fuerte, por eso el complejo tendrá un espín bajo. Seis electrones entrarán en los orbitales t2g, dejando a 0 sin aparear.
Ejercicio \(\PageIndex{1}\)
El tamaño de la división del campo cristalino solo influye la disposición de los electrones cuando se puede elegir entre emparejar los electrones y llenar los orbitales de mayor energía. ¿Para qué configuraciones de electrones d habrá una diferencia entre las configuraciones de espín alto y bajo en los complejos octaédricos?
- Respuesta
-
d4, d5, d6, y d7
Ejemplo \(\PageIndex{2}\): Teoría del campo cristalino para otras geometrías
La teoría del campo cristalino es aplicable a moléculas en geometrías diferentes de octaédrica. En los complejos octaédricos, recuerde que los lóbulos del grupo eg apuntan directamente a los ligandos. Para los complejos tetraédricos, los orbitales d permanecen en su lugar, pero ahora solo tenemos cuatro ligandos ubicados entre los ejes (Figura \(\PageIndex{4}\)). Ninguno de los orbitales apunta directamente a los ligandos tetraédricos. Sin embargo, el conjunto eg (a lo largo de los ejes cartesianos) se superpone con los ligandos menos que el conjunto t2g. Por analogía con el caso octaédrico, prediga el diagrama de energía para los orbitales d en un campo de cristal tetraédrico. Para evitar confusiones, el conjunto octaédrico, por ejemplo, se convierte en un conjunto e tetraédrico y el conjunto octaédrico t2g se convierte en un conjunto t2.
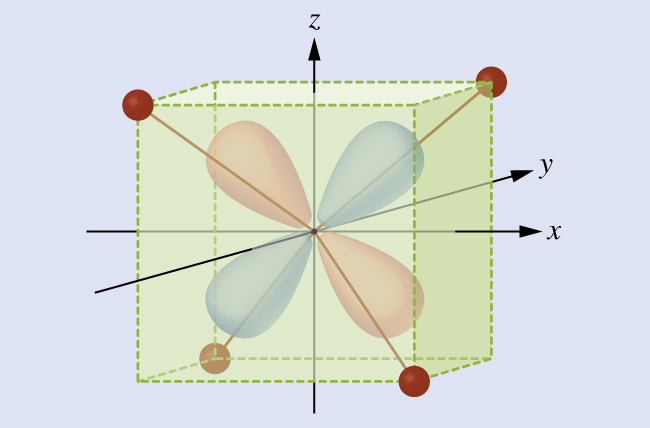
Figura \(\PageIndex{4}\): Este diagrama muestra la orientación de los ligandos tetraédricos con respecto al sistema de ejes de los orbitales.
Solución
Dado que la CFT se basa en la repulsión electrostática, los orbitales más cercanos a los ligandos se desestabilizarán y aumentarán de energía en relación con el otro conjunto de orbitales. La división es menor que para los complejos octaédricos porque la superposición es menor, por eso Δtet es usualmente pequeño \(\left(Δ_\ce{tet}=\dfrac{4}{9}Δ_\ce{oct}\right)\):
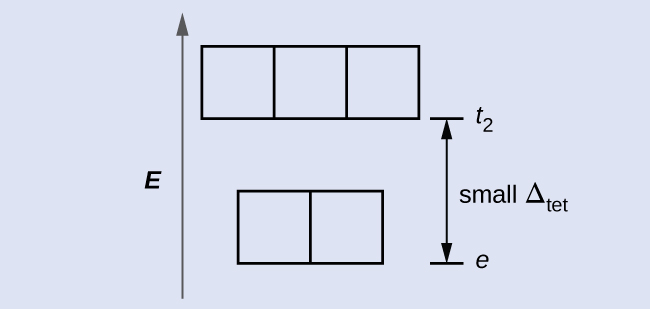
Ejercicio \(\PageIndex{2}\)
Explique cuántos pares de electrones no están apareados en un ion tetraédrico d4.
- Respuesta
-
4; porque Δtet es pequeño, todos los complejos tetraédricos son de alto espín y los electrones entran en los orbitales t2 antes de emparejarse
La otra geometría común es cuadrada plana. Se puede considerar una geometría plana cuadrada como una estructura octaédrica con un par de ligandos trans eliminados. Se supone que los ligandos eliminados están en el eje z. Esto cambia la distribución de los orbitales d, porque los orbitales en o cerca del eje z se vuelven más estables, y los que están en o cerca de los ejes x o y se vuelven menos estables. Esto causa que los conjuntos octaédricos de t2g y eg se dividan y den un patrón más complicado sin un Δoct simple. El patrón básico es:
Los momentos magnéticos de moléculas e iones
La evidencia experimental de las mediciones magnéticas apoya la teoría de los complejos de alto y bajo espín. Recuerde que las moléculas como el O2 que contienen los electrones desapareados son paramagnéticas. Las sustancias paramagnéticas se sienten atraídas por los campos magnéticos. Muchos complejos de metales de transición tienen electrones desapareados y por eso son paramagnéticos. Las moléculas como N2 e iones como Na+ y [Fe(CN)6]4− que no contienen electrones desapareados son diamagnéticas. Las sustancias diamagnéticas tienen una pequeña tendencia a ser repelidas por los campos magnéticos.
Cuando un electrón en un átomo o ion no está apareado, el momento magnético debido a su espín hace que todo el átomo o ion sea paramagnético. El tamaño del momento magnético de un sistema que contiene electrones no apareados está relacionado directamente con el número de electrones: cuanto mayor es el número de electrones no apareados, mayor es el momento magnético. Por lo tanto, el momento magnético observado se usa para determinar el número de electrones desapareados presentes. El momento magnético medido de espín bajo d6 [Fe(CN)6]4− confirma que el hierro es diamagnético, mientras que d6 [Fe(H2O)6]2+ de espín alto tiene cuatro electrones no apareados con un momento magnético que confirma esta disposición .
Los colores de los complejos de los metales de transición
Cuando los átomos o las moléculas absorben luz a la frecuencia adecuada, sus electrones se excitan a los orbitales de mayor energía. Para muchos átomos y moléculas del grupo principal, los fotones absorbidos están en el rango ultravioleta del espectro electromagnético, que no puede ser detectado por el ojo humano. Para los compuestos de coordinación, la diferencia de energía entre los orbitales d a veces permite que se absorban fotones en el rango visible.
El ojo humano percibe una mezcla de todos los colores, en las proporciones presentes en la luz del sol, como luz blanca. Los colores complementarios, los que se encuentran uno frente al otro en una rueda de colores, también se usan en la visión del color. El ojo percibe una mezcla de dos colores complementarios, en las proporciones adecuadas, como luz blanca. Asimismo, cuando falta un color en la luz blanca, el ojo ve su complemento. Por ejemplo, cuando los fotones rojos se absorben de la luz blanca, los ojos ven el color verde. Cuando los fotones violetas se eliminan de la luz blanca, los ojos ven el color amarillo limón. El color azul del ion [Cu(NH3)4]2+ resulta porque este ion absorbe la luz naranja y roja, dejando los colores complementarios de azul y verde (Figura \(\PageIndex{5}\)).
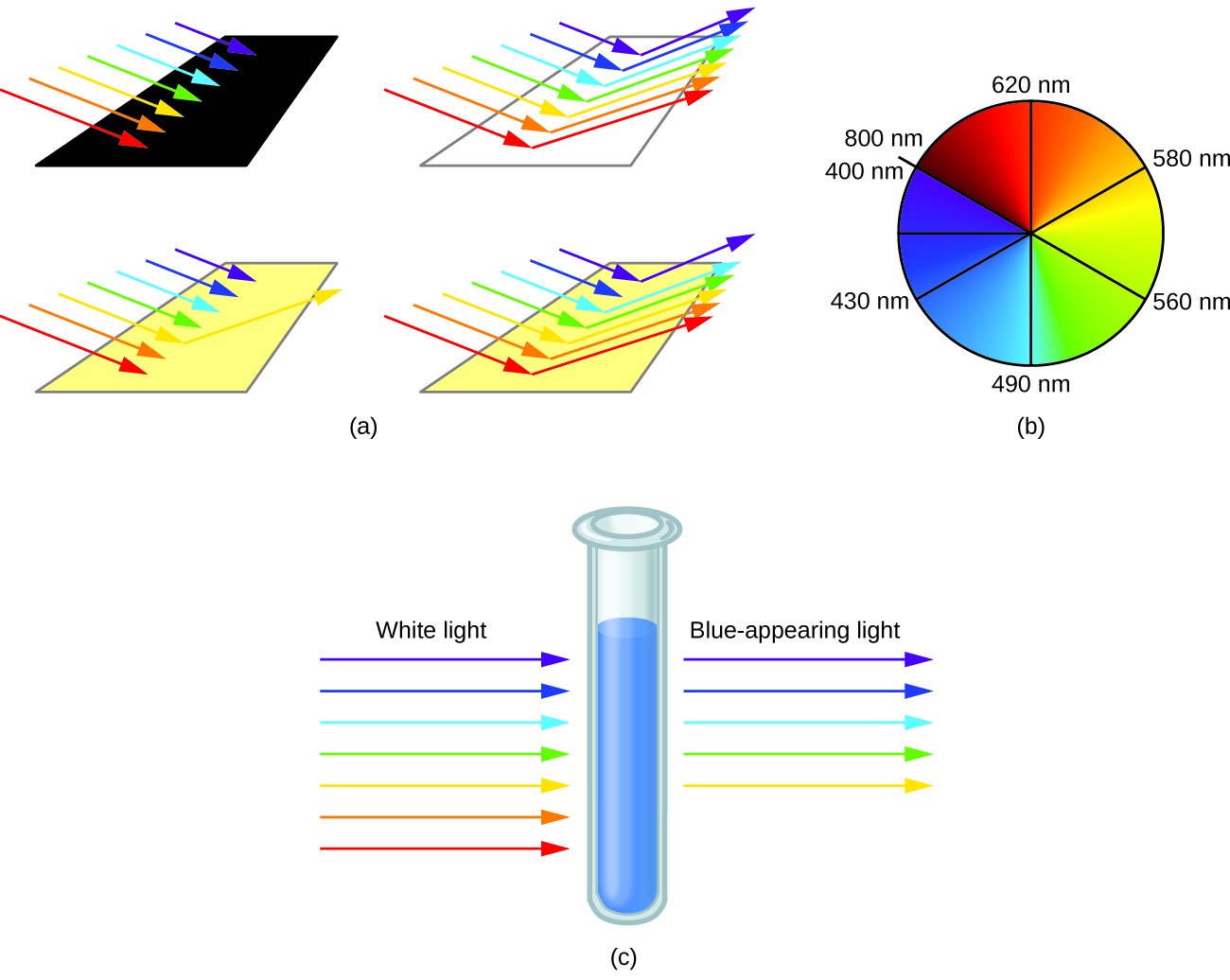
Figura \(\PageIndex{5}\): (a) Un objeto es negro si absorbe todos los colores de la luz. Si refleja todos los colores de la luz, es blanco. Un objeto tiene un color si absorbe todos los colores excepto uno, como esta tira amarilla. La tira también aparece amarilla si absorbe el color complementario de la luz blanca (en este caso, el índigo). (b) Los colores complementarios están ubicados directamente uno frente al otro en la rueda de colores. (c) Una solución de iones [Cu(NH3)4]2+ absorbe la luz roja y naranja, por eso la luz transmitida aparece como el color complementario, azul.
Ejemplo \(\PageIndex{3}\): Los colores de los complejos
El complejo octaédrico [Ti(H2O)6]3+ tiene un solo electrón d. Para excitar este electrón desde el orbital t2g del estado fundamental al orbital eg, este complejo absorbe luz de 450 a 600 nm. La absorbancia máxima corresponde a Δoct y se produce a 499 nm. Calcula el valor de Δoct en julios y prediga de qué color aparecerá la solución.
Solución
Usando la ecuación de Planck (consulte la sección sobre la energía electromagnética), calculamos:
\[v=\dfrac{c}{λ}\mathrm{\:so\:\dfrac{3.00×10^8\: m/s}{\dfrac{499\: nm×1\: m}{10^9\:nm}}=6.01×10^{14}\:Hz} \nonumber\]
\[E=hnu\mathrm{\:so\:6.63×10^{−34}\:\textrm{J⋅s}×6.01×10^{14}\:Hz=3.99×10^{−19}\:Joules/ion} \nonumber\]
Debido a que el complejo absorbe de 600 nm (naranja) a 450 (azul), se transmitirán las longitudes de onda índigo, violeta y roja, y el complejo aparecerá de color púrpura.
Ejercicio \(\PageIndex{3}\)
¿Un complejo que parece de color verde, absorbe fotones de qué longitudes de onda?
- Respuesta
-
rojo, 620–800 nm
Los cambios pequeños en las energías relativas de los orbitales entre los que los electrones están haciendo la transición pueden provocar cambios drásticos en el color de la luz absorbida. Por tanto, los colores de los compuestos de coordinación dependen de muchos factores. Como se muestra en la Figura \(\PageIndex{6}\), diferentes iones metálicos acuosos pueden tener diferentes colores. Además, diferentes estados de oxidación de un metal pueden producir diferentes colores, como se muestra para los complejos de vanadio en el enlace abajo.

Figura \(\PageIndex{6}\): Los orbitales d parcialmente llenos de los iones estables Cr3+ (aq), Fe3+ (aq) y Co2+ (aq) (izquierda, centro y derecha, respectivamente) producen varios colores. (crédito: Sahar Atwa)
Los ligandos específicos coordinados con el centro metálico también influyen el color de los complejos de coordinación. Por ejemplo, el complejo de hierro (II) [Fe(H2O)6]SO4 aparece de color azul verdoso porque el complejo de alto espín absorbe fotones en las longitudes de onda rojas (Figura \(\PageIndex{7}\)). A diferencia, el complejo de hierro (II) de bajo espín K4[Fe(CN)6] aparece de color amarillo pálido porque absorbe fotones violetas de mayor energía.

Figura \(\PageIndex{7}\): Tanto (a) el sulfato de hexaaquairon (II) como (b) el hexacianoferrato de potasio (II) contienen centros metálicos octaédricos de hierro d6 (II), pero absorben fotones en diferentes rangos del espectro visible.
En general, los ligandos de campo fuerte provocan una gran división en las energías de los orbitales d del átomo metálico central (Δoct grande). Los compuestos de coordinación de los metales de transición con estos ligandos son amarillos, naranjas o rojos porque absorben la luz violeta o azul de mayor energía. Por otro lado, los compuestos de coordinación de los metales de transición con los ligandos de campo débil a veces son de color azul-verde, azul o índigo porque absorben la luz amarilla, naranja o roja de menor energía.
Video \(\PageIndex{8}\): Mire este vídeo de la reducción de los complejos de vanadio para observar el efecto en el color causado por los cambios en los estados de oxidación.
Un compuesto de coordinación del ion Cu+ tiene una configuración d10 y todos los orbitales eg están llenos. Para excitar un electrón a un nivel superior, como el orbital 4p, se necesitan fotones de muy alta energía. Esta energía corresponde a las longitudes de onda muy cortas en la región ultravioleta del espectro. No se absorbe la luz visible por eso el ojo no ve ningún cambio y el compuesto parece blanco o incoloro. Por ejemplo, una solución que contiene [Cu(CN)2]- es incolora. Por otro lado, los complejos octaédricos de Cu2+ tienen una vacancia en los orbitales eg y los electrones se pueden excitar hasta este nivel. La longitud de onda (energía) de la luz absorbida corresponde a la parte visible del espectro, y los complejos de Cu2+ casi siempre son de color: azul, azul verdoso, violeta o amarillo (Figura \(\PageIndex{8}\)). Aunque CFT describe muchas propiedades de los complejos de coordinación, se requieren explicaciones de los orbitales moleculares (más allá del alcance introductorio proporcionado aquí) para comprender completamente el comportamiento de los complejos de coordinación.

Figura \(\PageIndex{8}\): (a) Los complejos de cobre (I) con configuraciones d10 como CuI tienden a ser incoloros, mientras que (b) los complejos de cobre (II) d9 como Cu(NO3)2·5H2O tienen colores brillantes.
Resumen
La teoría del campo cristalino considera las interacciones entre los electrones del metal y los ligandos como un simple efecto electrostático. La presencia de los ligandos cerca del ion metálico cambia las energías de los orbitales d del metal en relación con sus energías en el ion libre. Tanto el color como las propiedades magnéticas de un complejo se pueden atribuir a esta división del campo cristalino. La magnitud de la división (Δoct) depende de la característica de los ligandos unidos al metal. Los ligandos de campo fuerte producen grandes divisiones y favorecen los complejos de bajo espín, en los que los orbitales t2g se llenan por completo antes de que los electrones ocupen los orbitales eg. Los ligandos de campo débil favorecen la formación de los complejos de alto espín. Los orbitales t2g y eg se ocupan individualmente antes de que alguno esté doblemente ocupado.
Glosario
- división del campo cristalino (Δoct)
- diferencia de energía entre los orbitales t2g o eg o los orbitales t y e
- teoría del campo cristalino
- modelo que explica las energías de los orbitales en los metales de transición en términos de las interacciones electrostáticas con los ligandos, pero no incluye los enlaces de los ligandos metálicos
- orbitales eg
- conjunto de dos orbitales d que están orientados sobre los ejes cartesianos para los complejos de coordinación; en los complejos octaédricos, tienen mayor energía que los orbitales t2g
- isómeros geométricos
- isómeros que difieren en la forma en que los átomos se orientan en el espacio entre sí, lo que causa diferentes propiedades físicas y químicas
- complejo de alto espín
- complejo en el que los electrones maximizan el espín total por llenando todos los orbitales individualmente antes de emparejar dos electrones en los orbitales de menor energía
- complejo de baja espín
- complejo en el que los electrones minimizan el espín total de los electrones emparejandose en los orbitales de menor energía antes de llenar los orbitales de mayor energía
- energía de emparejamiento (P)
- energía requerida para colocar dos electrones con espines opuestos en un solo orbital
- serie espectroquímica
- clasificación de ligandos de acuerdo con la magnitud de la división del campo cristalino que causan
- ligando de campo fuerte
- ligando que causa divisiones más grandes del campo cristalino
- orbitales t2g
- conjunto de tres orbitales d alineados entre los ejes cartesianos para los complejos de coordinación; en los complejos octaédricos, su energía se reduce en comparación con los orbitales, por ejemplo, según CFT
- ligando de campo débil
- ligando que causa pequeñas divisiones del campo cristalino
Contribuyentes y atribuciones
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


