14.1: Adiciones Michael y eliminaciones beta
- Page ID
- 2419
14.1A: Overview of Michael addition and beta-elimination mechanisms
In chapter 11 we learned about nucleophilic carbonyl addition reactions, including the formation of hemiacetals, hemiketals, and Schiff bases. In all of these reactions, a nucleophile directly attacks a carbonyl carbon.

If, however, the electrophilic carbonyl is beta-unsaturated - if, in other words, it contains a double bond in the Cα-Cβ position, conjugated to the carbonyl - a different reaction pathway is possible. A resonance structure can be drawn in which the beta-carbon has a positive charge, meaning that the beta-carbon also has the potential to be an electrophilic target.
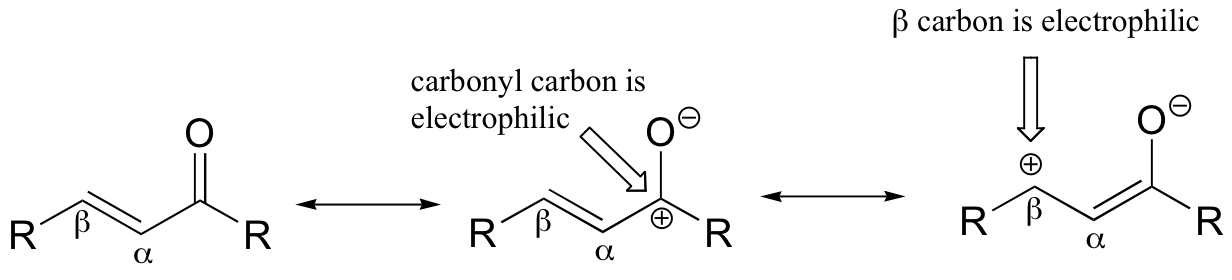
If a nucleophile attacks at the beta-carbon, an enol or enolate intermediate results (step 1 below). Usually, this intermediate collapses and the alpha-carbon is protonated (step 2). This type of reaction is known as a 'conjugate addition' or a 'Michael addition'.

The reverse of a Michael addition is called a 'beta-elimination':

This is often referred to as an 'E1cb' mechanism. The E stands for 'elimination'; the numeral 1 refers to the fact that, like the SN1 mechanism, it is a stepwise reaction with first order kinetics. The 'cb' designation refers to the intermediate, which is the conjugate base of the starting compound.
Because both Michael additions and E1cb reactions proceed through a resonance-stabilized carbanion intermediate, it is essential that a carbonyl group be located in an appropriate position. This requirement is evident in the beta-elimination below, which is part of the biosynthesis of aromatic amino acids. The elimination does not proceed directly, because there is no carbonyl available in the starting compound to stabilize a carbanion intermediate. Before elimination can occur, a hydroxyl group must be oxidized in step 1 to form a ketone (don't worry yet about how this first oxidation step works - we will learn all about this kind of reaction in section 16.4).
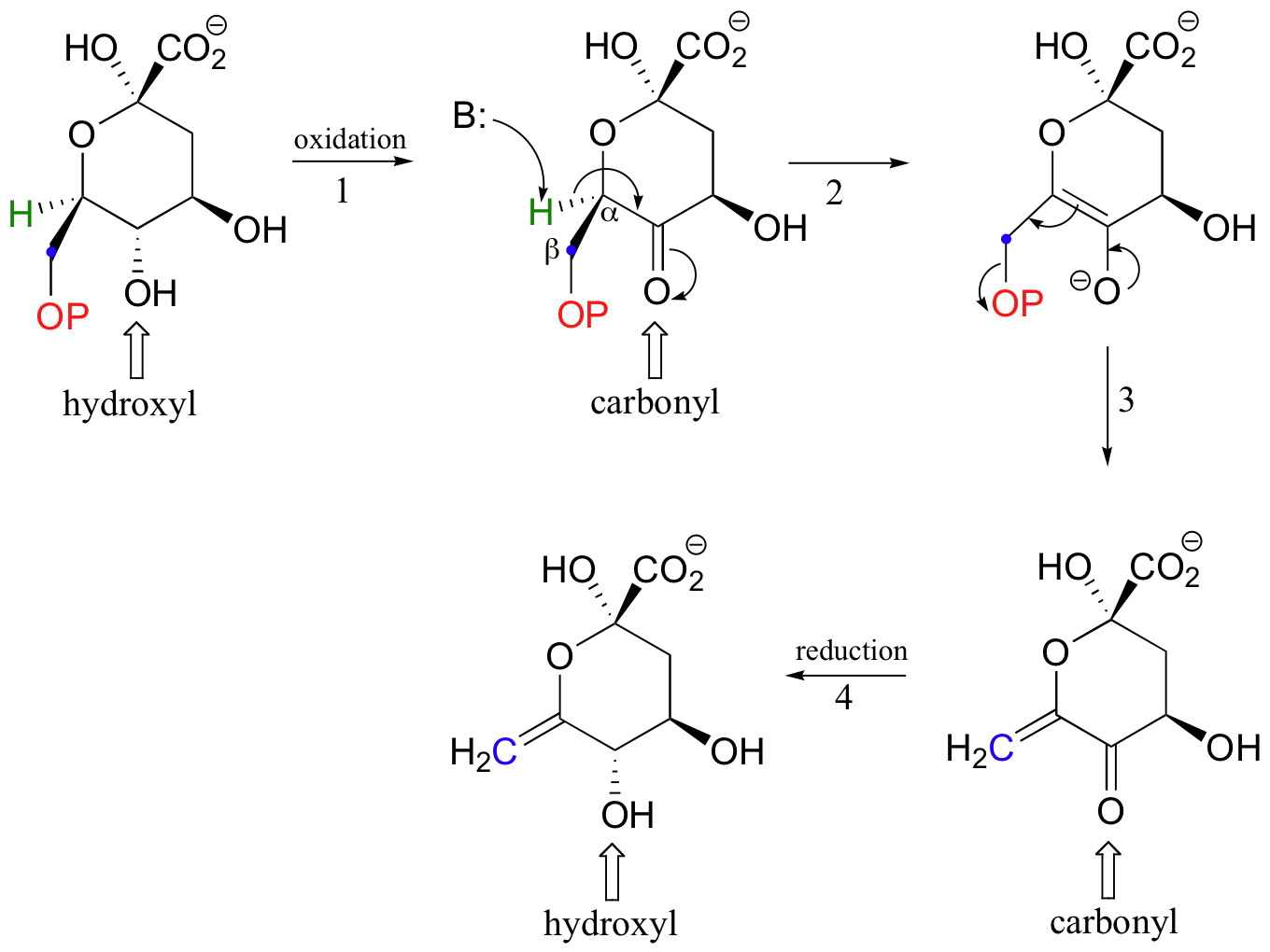
With the carbonyl group in place, the molecule is set up to undergo beta-elimination. Once the elimination is accomplished (steps 2 and 3), the ketone is converted back to an alcohol (step 4-this reduction reaction is also covered in section 16.4).
Alkene additions and beta-eliminations can also occur at positions that are not conjugated to an electron-withdrawing group such as a carbonyl. An electrophilic addition to an alkene, which is a very diferent addition mechanism, proceeds through a carbocation intermediate, and is the topic of section 15.2.
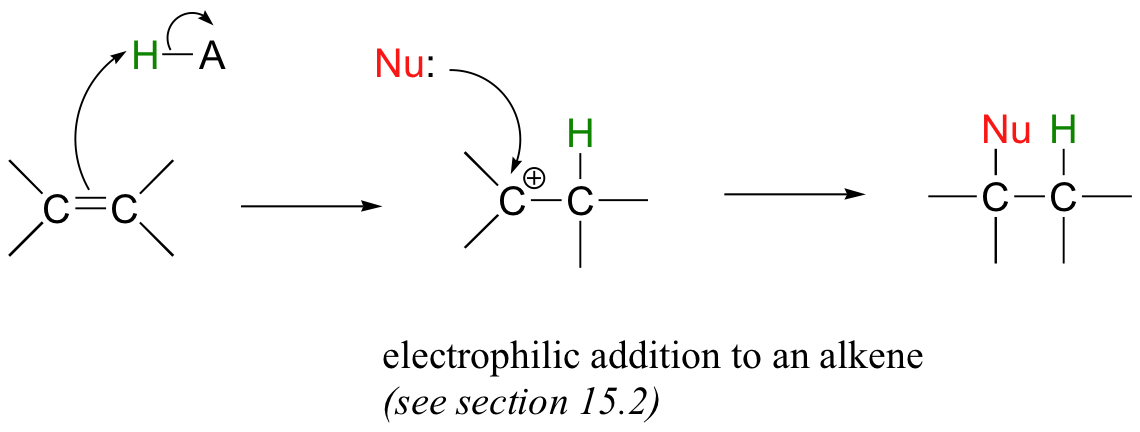
The so-called 'E1' and 'E2' elimination mechanisms, which are covered later in this chapter (section 14.3), also proceed without the need for an adjacent carbonyl group.

For now, we will concentrate on alkene addition and beta-elimination mechanisms that involve negatively-charged intermediates.
14.1B: Stereochemistry of Michael additions and β-eliminations
Addition to an alkene can follow two possible stereochemical courses: the nucleophilic group and the proton can add either to the same side of the plane of the alkene (a syn addition), or to opposite sides (an anti addition).

In the degradation pathway of fatty acids, the following conjugate addition takes place, catalyzed by enoyl-CoA hydratase. (Because it is a water molecule that is being added, this addition is often referred to a 'hydration' reaction).
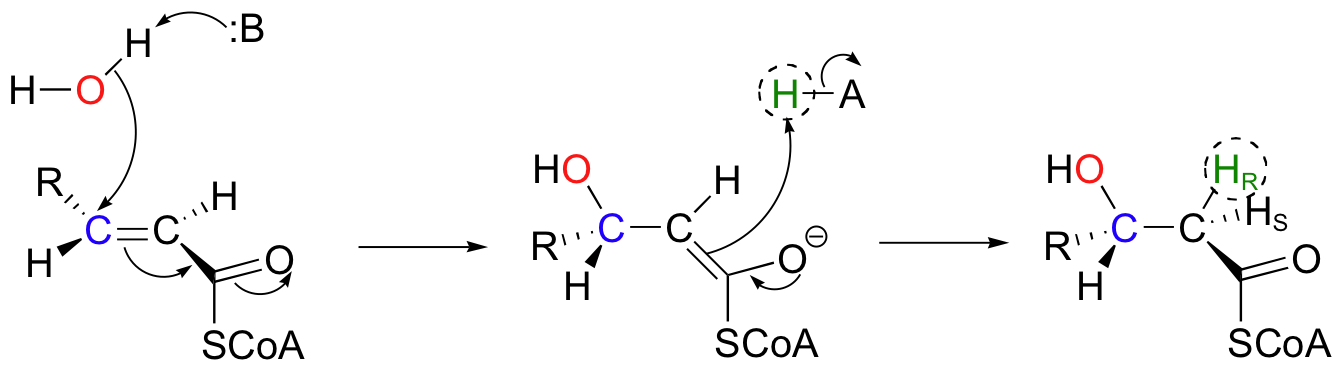
Notice the stereochemical details: this is a syn addition to a trans double bond, resulting in a (S)-3-hydroxy thioester. The pro-R hydrogen on Cα of the product is added in the reaction, while the pro-S hydrogen comes from the starting alkene.
Directing the stereochemical outcome of this addition reaction is an important part of the enzyme's job as a catalyst. Notice that addition of water to enoyl-CoA, the starting alkene for this reaction, could hypothetically occur by four different stereochemical pathways, two syn and two anti. This is easier to see if we imagine the reaction running in D2O, so that we can distinguish between the deuterium that is added to the double bond and the hydrogen that was already there.
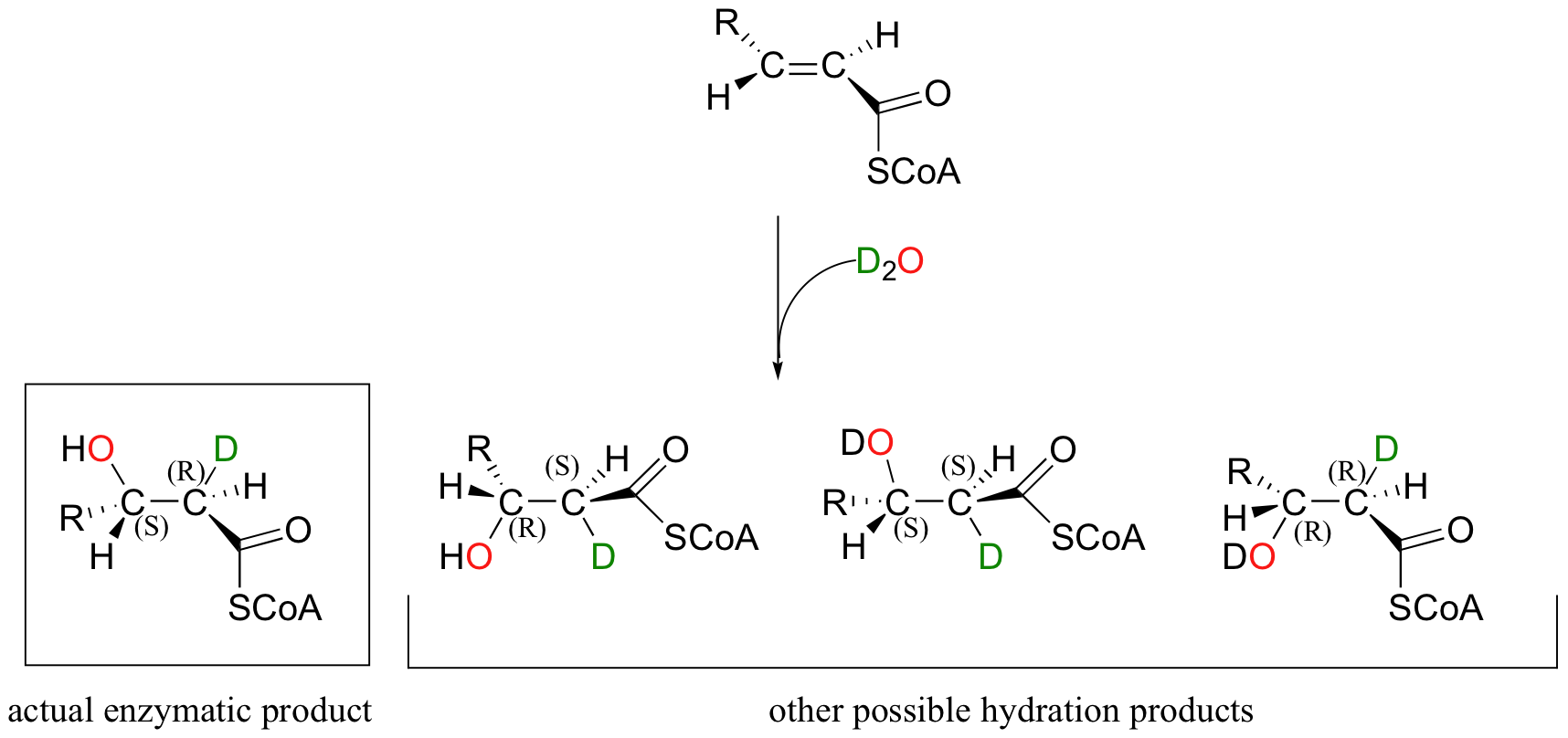
In order to ensure that the correct stereoisomer is formed, the enzyme must bind the substrate in the active with a very specific orientation relative to the nucleophilic water molecule and the proton donating group.
Next, we will consider an enzymatic dehydration reaction (elimination of water) that, without considering stereochemistry, would appear to be the reverse of the enoyl-CoA hydration reaction. The dehydration reaction is part of the metabolic pathway for the synthesis of fatty acids, whereas the hydration reaction is part of fatty acid degradation.
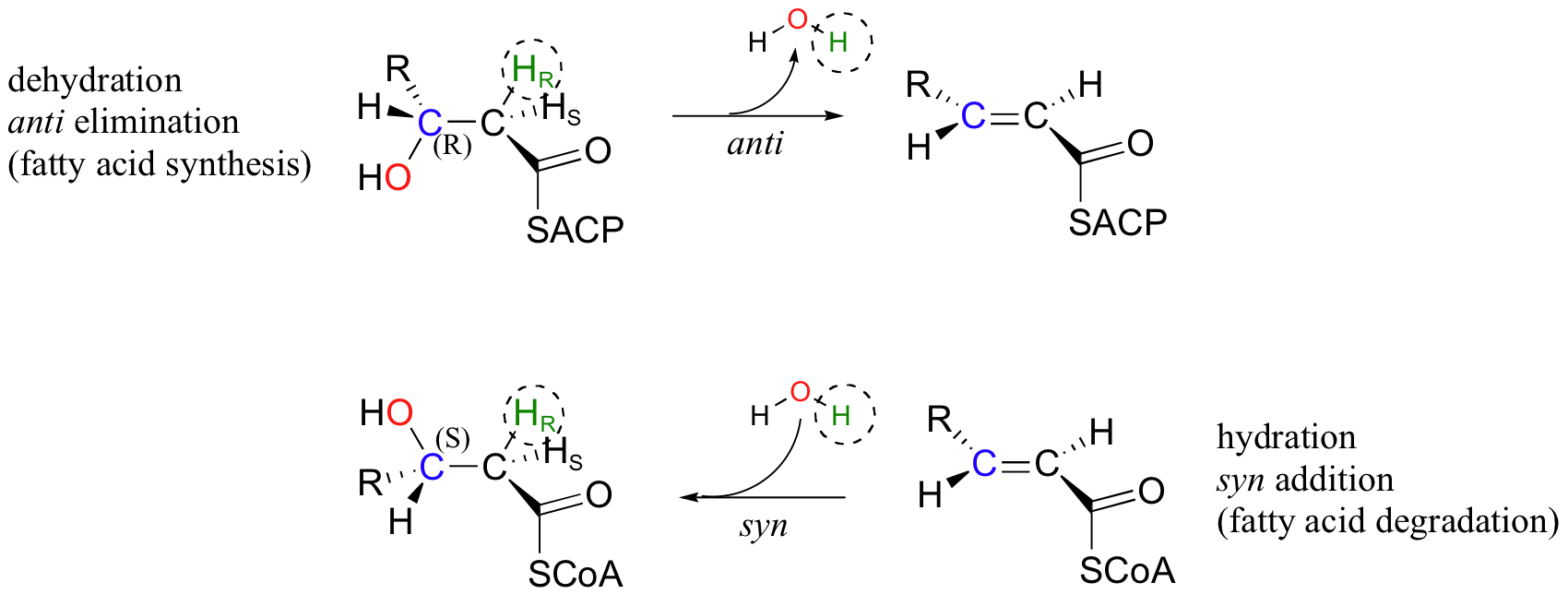
There are several differences between these two reactions that make it plain that they are not the exact reverse of one another, and are catalyzed by two different enzymes. First, the elimination reaction involves an ACP thioester (section 12.3), while the addition reaction involves an -SCoA thioester. Also, the elimination is anti, and starts with R stereochemistry at the beta-carbon, whereas the addition reaction is syn, and results in S stereochemistry at the beta-carbon. This is a nice illustration, in a stereochemical context, of a idea we have seen before: metabolic pathways going in opposite directions are usually not the exact reverse of one another. You will learn in your biochemistry class how this idea is extremely important in metabolic regulation.
14.1C: An NMR experiments to determine the stereochemistry of a Michael addition
In a step in the citric acid cycle, anti addition of water to the double bond in fumarate leads to (S)-malate.
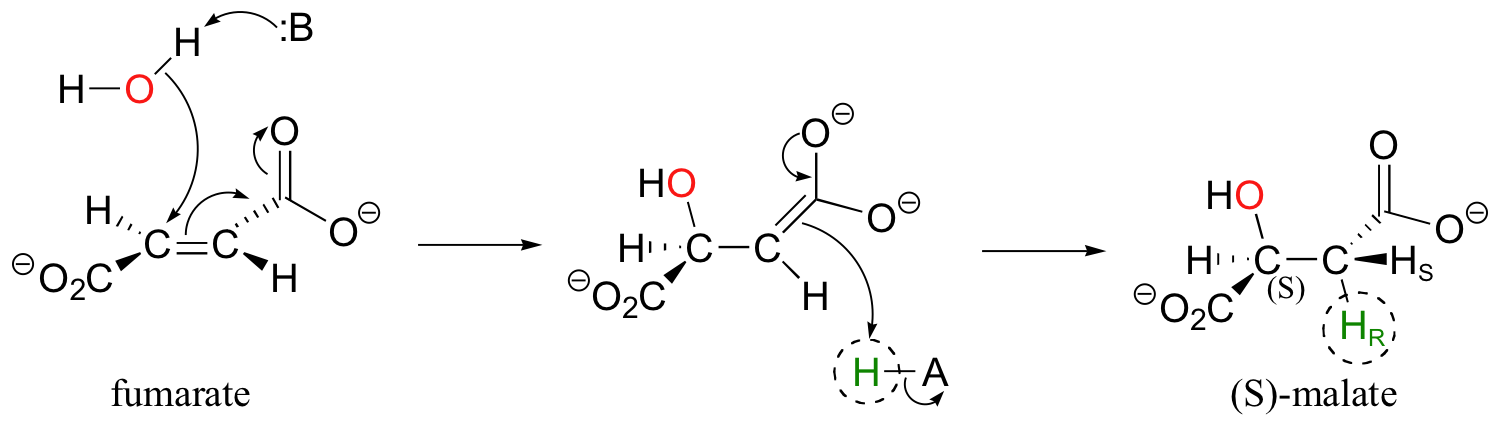
Fumarase, the enzyme catalyzing this reaction, was one of the first of its type for which the stereochemical outcome was experimentally determined. In the early 1960's researchers, who did not yet understand the stereochemical details of this reaction, incubated fumarate with fumarase enzyme in D2O. They then compared the 1H-NMR spectrum of the resulting C3-deuterated malate to those of laboratory-synthesized (2S, 3S)-3-deuteromalate (J. Am. Chem. Soc. 1961, 83, 3634).
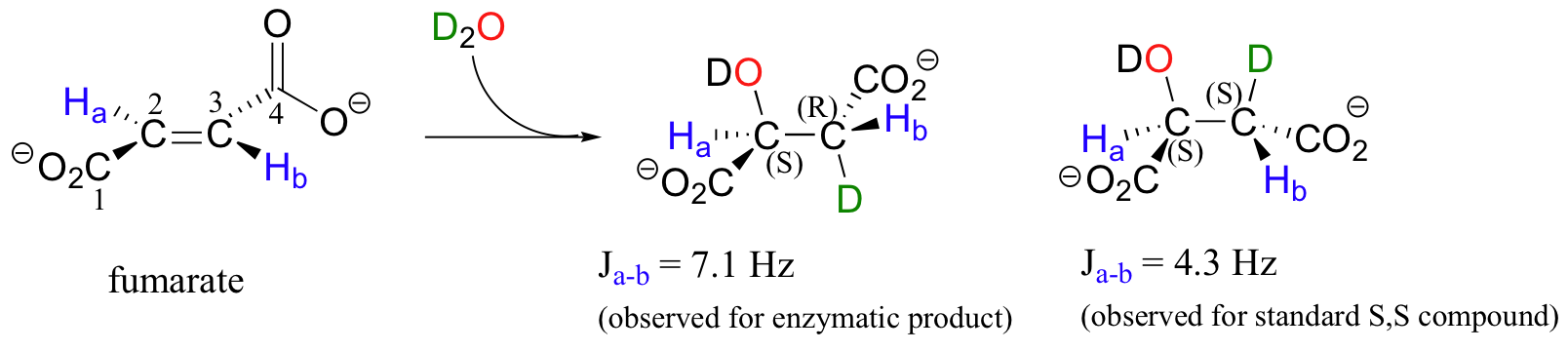
The spectrum of the enzymatically synthesized product was not the same as the laboratory synthesized (2S, 3S) standard; in particular, the coupling constant between the C2 and C3 protons (Ha and Hb in the above figure) was 4.3 Hz for the standard and 7.1 Hz for the enzymatic product. The stereochemistry at C2 of enzymatically synthesized malate was known to be S, so the researchers concluded that the enzymatic product in D2O had the (2S,3R) configuration, meaning that the addition of water had to be anti instead of syn. The (2S,3R) stereochemistry of the enzymatic product in D2O was verified years later in a study by a different research team (Biochem. Biophys. Res. Comm. 1983, 115, 1048).
14.1D: More examples of elimination and addition reactions
Enolates are the most common intermediate in E1cB eliminations, but, as in aldol reactions, imine-based mechanisms are also possible. Dehydroquinate, a metabolite in aromatic amino acid synthesis, is subjected to the following syn elimination which proceeds through imine and enamine intermediates.
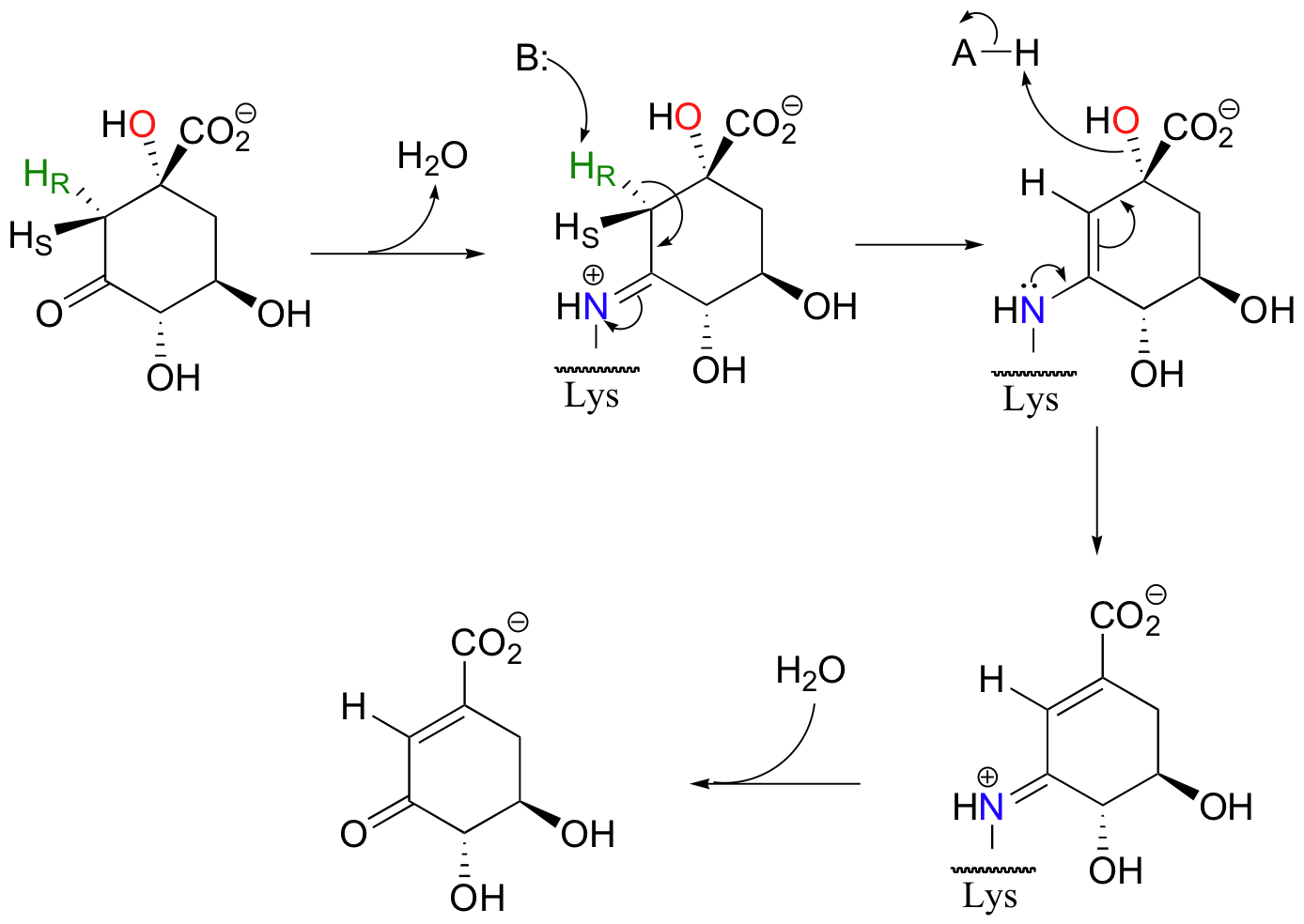
As with aldolases, an active site lysine supplies the necessary amine group for imine formation.
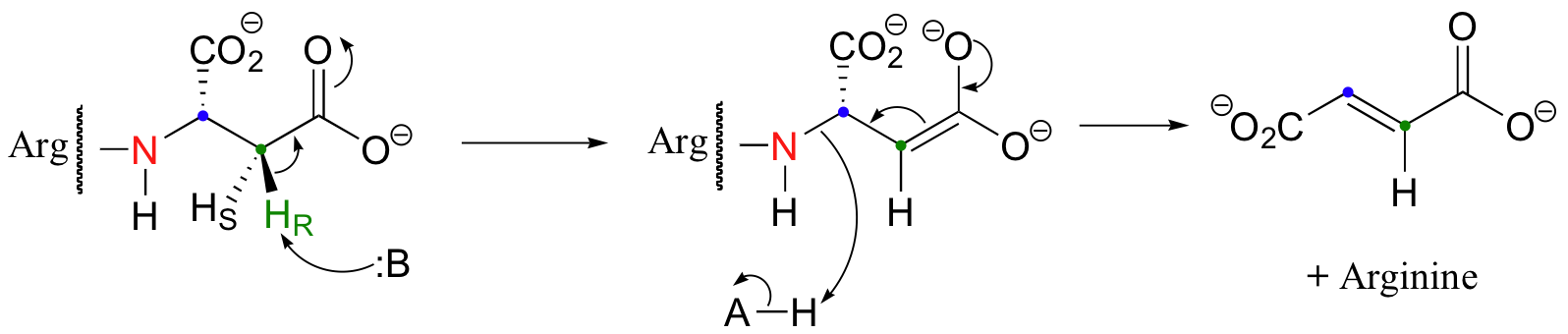
Thus far we have only seen additions and eliminations of water (ie. hydrations and dehydrations). Argininosuccinate lyase, an enzyme in the urea cycle (a series of reactions in which the amine group of amino acids is transferred to urea for elimination in the urine), catalyzes an anti elimination with arginine as the leaving group.
A very interesting linked elimination-addition reaction is catalyzed by aconitase, an enzyme in the citric acid cycle. In this reaction, a hydrogen and an adjacent hydroxyl group on citrate switch places, resulting in the formation of isocitrate, a constitutional isomer.
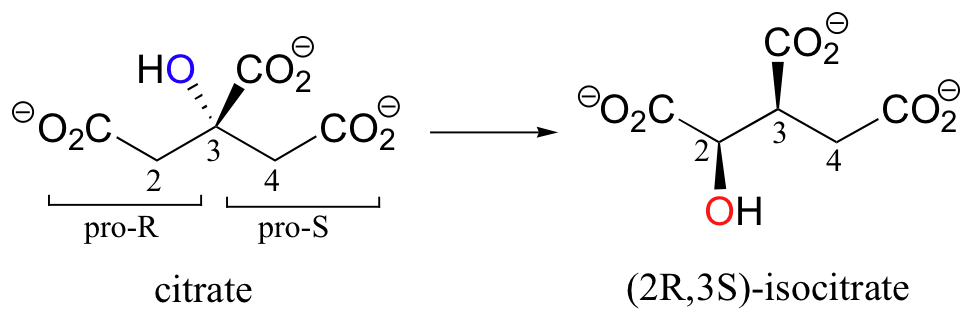
You may recall from section 3.10A that citrate is a prochiral molecule, with pro-R and pro-S 'arms' bonded to the central tetrahedral carbon. Because these 'arms' are prochiral, an enzyme is able to distinguish between the two, and the isomerization takes place specifically on the pro-R arm. The movement of the hydroxyl group is accomplished by elimination and then re-addition of water. In the elimination step, it is the pro-R hydrogen (on the pro-R arm) that is removed, meaning that this is an anti elimination.

Isotopic labeling experiments have shown that the pro-R proton removed from citrate is retained by the enzyme and added back to isocitrate, but the hydroxide comes from solvent water. Think about the implications of that last statement: the pro-R proton is removed from one side of C2, then the exact same proton is added to C3 on the opposite side! How did this proton move over and around so fast? This question has intrigued researchers for years. It now appears that, in fact, the proton does not move at all - rather, after the first elimination step is completed, the entire alkene intermediate flips over 180 degrees in the active site.
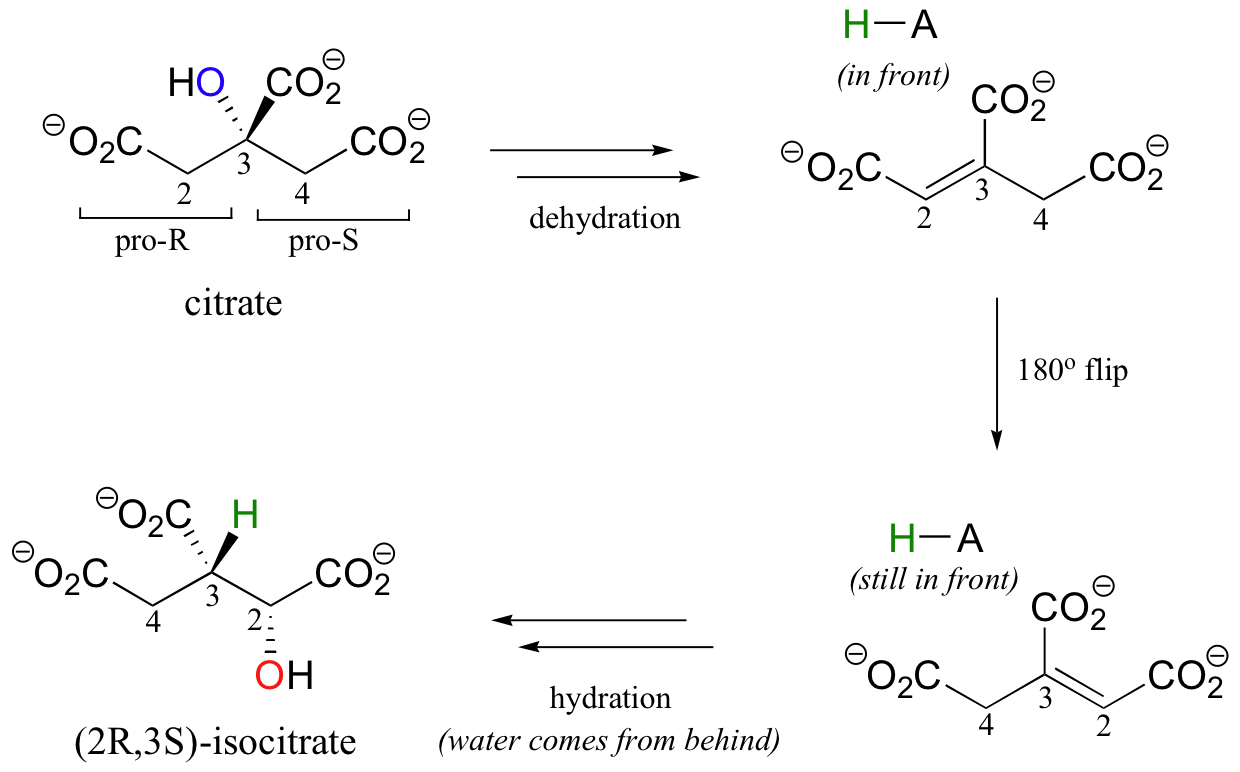
This allows the abstracted proton - which has been sitting on an active site acid-base residue - to be added to the correct carbon and the correct side of the double bond.
As a final E1cb example, it is worth noting that nonenzymatic aldol reactions (section 13.3) often do not stop at the beta-hydroxycarbonyl stage, but rather go on to a dehydration step:
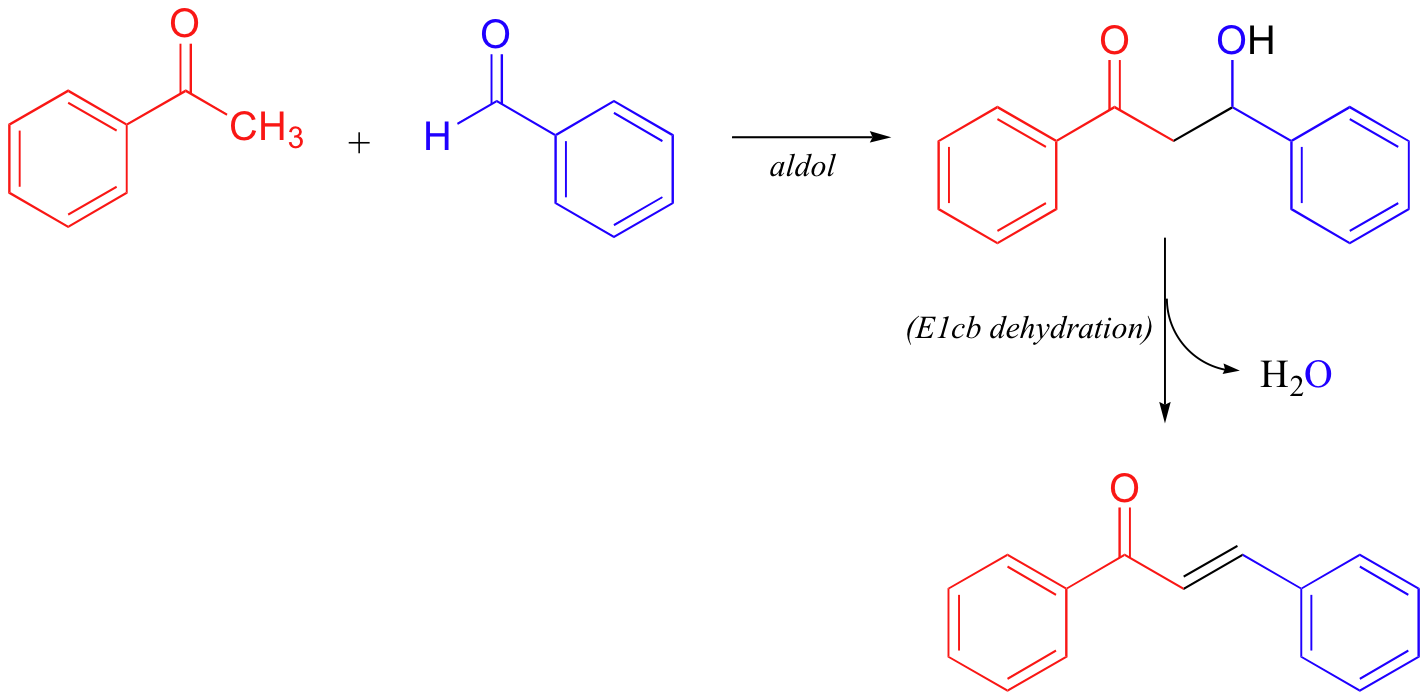
The dehydration step is especially likely in examples such as that depicted above, where the formation of an additional double bond results in an extended pi-bonding network.
A very well known and useful Michael addition reaction in laboratory synthesis is the Robinson annulation (the term ‘annulation’ comes from the Latin annulus, meaning ‘ring’. As you can see, this is a ring-forming reaction. Sir Robert Robinson was an English chemist who won the 1947 Nobel Prize in Chemistry).

A Robinson annulation reaction starts with a (base-promoted) Michael addition of an alpha-carbon nucleophile to an alpha-beta-unsaturated carbonyl, followed by an aldol condensation (to form the ring) and finally a dehydration. You will be invited to draw a complete mechanism for the above reaction (and to predict the starting materials or products of some other Robinson annulation reactions) in the end-of chapter problems.


