12.2: Las tasas de las reacciones químicas
- Page ID
- 1894
habilidades para desarrollar
- Definir la velocidad de las reacciones químicas
- Derivar las expresiones de tasa de la ecuación balanceada para una reacción química dada
- Calcular las tasas de una reacción a partir de los datos experimentales
Una tasa es una medida de cómo algunas propiedades varían con el tiempo. La velocidad es una tasa familiar que expresa la distancia recorrida por un objeto en un período de tiempo determinado. El salario es una tasa que representa la cantidad del dinero ganado por una persona que trabaja durante un período de tiempo determinado. Del mismo modo, la velocidad de una reacción química es una medida de la cantidad del reactivo que se consume, o cuánto producto se produce, por la reacción en un período de tiempo determinado.
La velocidad de la reacción es el cambio en la cantidad de un reactivo o producto por la unidad de tiempo. Por lo tanto, las velocidades de reacción se determinan midiendo la dependencia del tiempo de algunas propiedades que pueden estar relacionadas con las cantidades de reactivo o producto. Las tasas de reacciones que consumen o producen sustancias gaseosas, por ejemplo, se determinan convenientemente midiendo los cambios en el volumen o la presión. Para las reacciones que involucran una o más sustancias coloreadas, las tasas se pueden controlar mediante las mediciones de absorción de luz. Para las reacciones que involucran electrolitos acuosos, las tasas se pueden medir a través de cambios en la conductividad de una solución.
Para los reactivos y los productos en solución, sus cantidades relativas (concentraciones) se usan convenientemente para expresar las velocidades de la reacción. Si medimos la concentración de peróxido de hidrógeno, H2O2, en una solución acuosa, encontramos que cambia lentamente con el tiempo a medida que el H2O2 se descompone, de acuerdo con la ecuación:
La velocidad a la que se descompone el peróxido de hidrógeno se puede expresar en términos de la velocidad de cambio de su concentración, como se muestra aquí:
\[\begin{align*}
\ce{rate\: of\: decomposition\: of\: H_2O_2}
&=\mathrm{−\dfrac{change\: in\: concentration\: of\: reactant}{time\: interval}}\\[5pt]
&=−\dfrac{[\ce{H2O2}]_{t_2}−[\ce{H2O2}]_{t_1}}{t_2−t_1}\\[5pt]
&=−\dfrac{Δ[\ce{H2O2}]}{Δt}
\end{align*}\]
Esta representación matemática del cambio en la concentración de especies a lo largo del tiempo es la expresión de velocidad para la reacción. Los corchetes indican concentraciones molares, y el símbolo delta (Δ) indica "cambio en". Por lo tanto, \([\ce{H2O2}]_{t_1}\) representa la concentración molar de peróxido de hidrógeno en algún momento t1; igualmente, \([\ce{H2O2}]_{t_2}\) representa la concentración molar de peróxido de hidrógeno en un momento que sigue t2; y Δ [H2O2] representa el cambio en la concentración molar de peróxido de hidrógeno durante el intervalo de tiempo Δt (es decir, t2 - t1). Como la concentración de reactivo disminuye a medida que avanza la reacción, Δ[H2O2] es una cantidad negativa; colocamos un signo negativo delante de la expresión porque las velocidades de reacción son, por convención, cantidades positivas. La Figura \(\PageIndex{1}\) proporciona un ejemplo de datos recopilados durante la descomposición de H2O2.
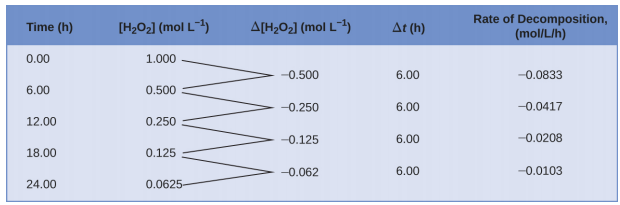
Para obtener los resultados tabulados para esta descomposición, se midió la concentración de peróxido de hidrógeno cada 6 horas en el transcurso de un día a una temperatura constante de 40 °C. Las tasas de reacción se calcularon para cada intervalo de tiempo dividiendo el cambio en la concentración por el incremento de tiempo correspondiente, como se muestra aquí para el primer período de 6 horas:
\[\dfrac{−Δ[\ce{H2O2}]}{Δt}=\mathrm{\dfrac{−(0.500\: mol/L−1.000\: mol/L)}{(6.00\: h−0.00\: h)}=0.0833\: mol\:L^{−1}\:h^{−1}}\]
Tenga en cuenta que las velocidades de reacción varían con el tiempo, disminuyendo a medida que avanza la reacción. Los resultados para el último período de 6 horas producen una velocidad de reacción de:
\[\dfrac{−Δ[\ce{H2O2}]}{Δt}=\mathrm{\dfrac{−(0.0625\:mol/L−0.125\:mol/L)}{(24.00\:h−18.00\:h)}=0.0104\:mol\:L^{−1}\:h^{−1}}\]
Este comportamiento indica que la reacción se ralentiza continuamente con el tiempo. El uso de las concentraciones al principio y al final de un período de tiempo durante el cual la velocidad de reacción está cambiando da como resultado el cálculo de una velocidad promedio para la reacción durante este intervalo de tiempo. En cualquier momento específico, la velocidad a la que se produce una reacción se conoce como la velocidad instantánea. La velocidad instantánea de una reacción en el "tiempo cero", cuando comienza la reacción, es su velocidad inicial. Considere la analogía de un automóvil que se desacelera cuando se acerca a una señal de alto. La velocidad inicial del vehículo, análoga al comienzo de una reacción química, sería la lectura del velocímetro en el momento en que el conductor comienza a presionar los frenos (t0). Unos momentos después, la tasa instantánea en un momento específico, llamada t1, sería algo más lenta, como lo indica la lectura del velocímetro en ese momento. A medida que pasa el tiempo, la tasa instantánea continuará cayendo hasta llegar a cero, cuando el automóvil (o reacción) se detiene. A diferencia de la velocidad instantánea, el velocímetro no indica la velocidad promedio del automóvil; pero se puede calcular como la relación entre la distancia recorrida y el tiempo requerido para detener completamente el vehículo (Δt). Al igual que el automóvil que desacelera, la velocidad promedio de una reacción química caerá en algún lugar entre sus velocidades iniciales y finales.
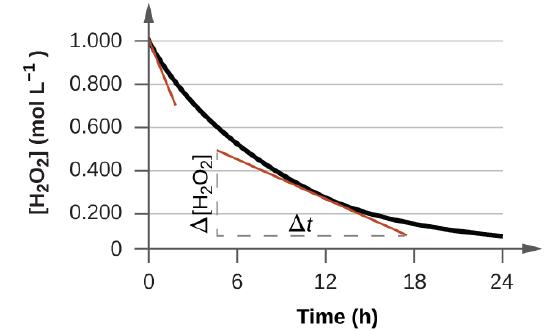
La velocidad instantánea de una reacción se puede determinar de dos maneras. Si las condiciones experimentales permiten la medición de los cambios de concentración en intervalos de tiempo muy cortos, entonces las tasas promedio calculadas como se describió anteriormente proporcionan aproximaciones razonablemente buenas de tasas instantáneas. Alternativamente, se puede usar un procedimiento gráfico que, en efecto, produzca los resultados que se obtendrían si fueran posibles mediciones de intervalos de tiempo cortos. Si hacemos un gráfico de la concentración de peróxido de hidrógeno contra al tiempo, la velocidad instantánea de descomposición de H2O2 en cualquier momento t viene dada por la pendiente de una línea recta que es tangente a la curva en ese momento (Figura \(\PageIndex{2}\)). Podemos usar el cálculo para evaluar las pendientes de tales líneas tangentes, pero el procedimiento para hacerlo está más allá del alcance de este capítulo.
TASAS DE REACCIÓN EN EL ANÁLISIS: TIRAS DE PRUEBA PARA EL URINÁLISIS
A veces, los médicos usan las tiras de prueba desechables para medir las cantidades de varias sustancias en la orina de un paciente (Figura \(\PageIndex{2}\)). Estas tiras reactivas contienen varios reactivos químicos, incrustados en pequeñas almohadillas en varios lugares a lo largo de la tira, que pasan por cambios de color al exponerse a concentraciones suficientes de sustancias específicas. Las instrucciones de uso de las tiras reactivas a veces enfatizan que el tiempo de lectura adecuado es crítico para obtener resultados óptimos. Este énfasis en el tiempo sugiere que los aspectos cinéticos de las reacciones químicas que ocurren en la tira de prueba son consideraciones importantes.
La prueba de glucosa urinaria se basa en un proceso de dos pasos representado por las ecuaciones químicas que se muestran aquí:
\[\ce{C6H12O6 + O2}\underset{\large\textrm{catalyst}}{\xrightarrow{\hspace{45px}}}\ce{C6H10O6 + H2O2} \label{eq1}\]
La ecuación \(\ref{eq1}\) representa la oxidación de la glucosa en la orina para producir la glucolactona y el peróxido de hidrógeno. El peróxido de hidrógeno producido posteriormente oxida el ion yoduro incoloro para producir el yodo de color marrón (Ecuación \(\ref{eq2}\)), que se puede detectar visualmente. Algunas tiras incluyen una sustancia adicional que reacciona con el yodo para producir un cambio de color más distintivo.
Las dos reacciones de prueba que se muestran arriba son inherentemente muy lentas, pero sus velocidades aumentan con la ayuda de las enzimas especiales incrustadas en la almohadilla de la tira de prueba. Este es un ejemplo de catálisis, un tema discutido más adelante en este capítulo. Una tira de prueba de glucosa típica para usar con orina requiere aproximadamente 30 segundos para completar las reacciones de formación de color. Leyendo el resultado demasiado pronto podría llevar a uno a concluir que la concentración de glucosa de la muestra de orina es más baja de lo que realmente es (un resultado falso negativo). Esperando demasiado tiempo para evaluar el cambio de color puede conducir a un falso positivo debido a la oxidación más lenta (no catalizada) del ion yoduro por otras sustancias que se encuentran en la orina.

Las tasas de reacción relativas
La velocidad de una reacción se puede expresar en términos del cambio en la cantidad de cualquier reactivo o producto, y se puede derivar simplemente de la estequiometría de la reacción. Considere la reacción representada por la siguiente ecuación:
\[\ce{2NH3}(g)⟶\ce{N2}(g)+\ce{3H2}(g)\]
Los factores estequiométricos derivados de esta ecuación se pueden usar para relacionar las velocidades de reacción de la misma manera que se usan para las cantidades de reactivo y producto relacionadas. La relación entre las velocidades de reacción expresadas en términos de producción de nitrógeno y consumo de amoníaco, por ejemplo, es:
\[\mathrm{−\dfrac{Δmol\: NH_3}{Δ\mathit t}×\dfrac{1\: mol\: N_2}{2\: mol\: NH_3}=\dfrac{Δmol\:N_2}{Δ\mathit t}}\]
Podemos expresar esto de manera más simple sin mostrar las unidades del factor estequiométrico:
\[−\dfrac{1}{2}\dfrac{\mathrm{Δmol\:NH_3}}{Δt}=\dfrac{\mathrm{Δmol\:N_2}}{Δt}\]
Tenga en cuenta que se ha agregado un signo negativo para tener en cuenta los signos opuestos de los dos cambios de cantidad (la cantidad de reactivo está disminuyendo mientras que la cantidad del producto está aumentando). Si los reactivos y productos están presentes en la misma solución, las cantidades molares se pueden reemplazar por concentraciones:
\[−\dfrac{1}{2}\dfrac{Δ[\ce{NH3}]}{Δt}=\dfrac{Δ[\ce{N2}]}{Δt}\]
De manera similar, la tasa de formación de H2 es tres veces la tasa de formación de N2 porque se forman tres moles de H2 durante el tiempo requerido para la formación de un mol de N2:
\[\dfrac{1}{3}\dfrac{Δ[\ce{H2}]}{Δt}=\dfrac{Δ[\ce{N2}]}{Δt}\]
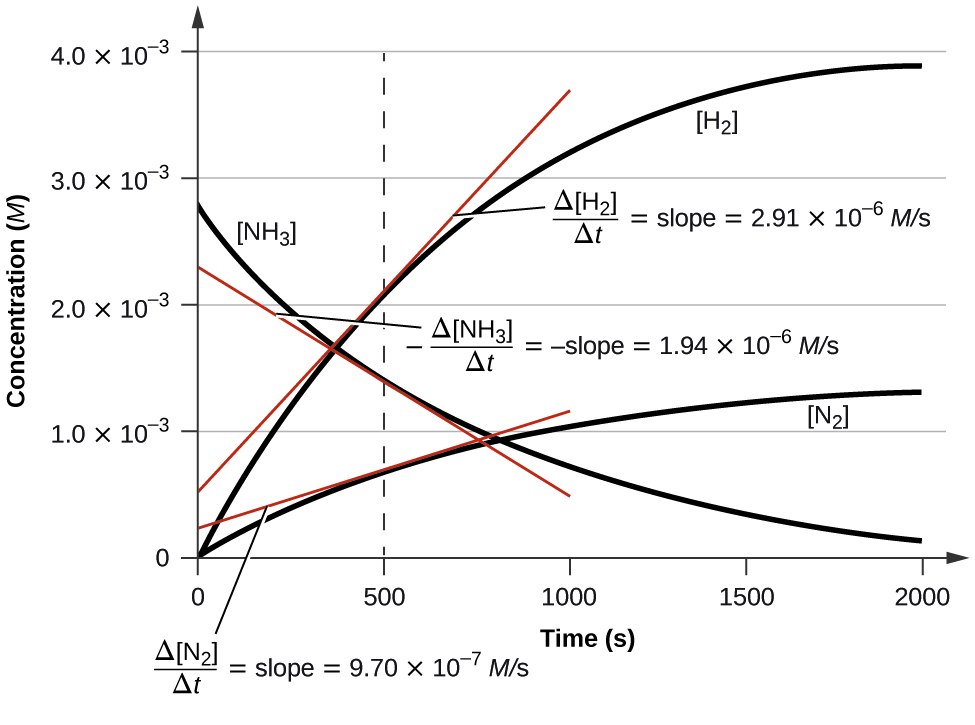
Figura \(\PageIndex{3}\) ilustra el cambio en las concentraciones a lo largo del tiempo para la descomposición del amoníaco en el nitrógeno e el hidrógeno a 1100 °C. Podemos ver por las pendientes de las tangentes dibujadas en t = 500 segundos que las tasas instantáneas del cambio en las concentraciones de los reactivos y los productos están relacionadas por sus factores estequiométricos. Se observa que la tasa de producción de hidrógeno, por ejemplo, es tres veces mayor que la de la producción del nitrógeno:
Ejemplo \(\PageIndex{1}\): EXPRESIONES PARA LAS TASAS DE REACCIÓN RELATIVAS
El primer paso en la producción del ácido nítrico es la combustión del amoníaco:
\[\ce{4NH3}(g)+\ce{5O2}(g)⟶\ce{4NO}(g)+\ce{6H2O}(g) \nonumber \]
Escriba las ecuaciones que relacionan las tasas de consumo de los reactivos y las tasas de formación de los productos.
Solución
Teniendo en cuenta la estequiometría de esta reacción homogénea, las tasas para el consumo de los reactivos y la formación de los productos son:
\[−\dfrac{1}{4}\dfrac{Δ[\ce{NH3}]}{Δt}=−\dfrac{1}{5}\dfrac{Δ[\ce{O2}]}{Δt}=\dfrac{1}{4}\dfrac{Δ[\ce{NO}]}{Δt}=\dfrac{1}{6}\dfrac{Δ[\ce{H2O}]}{Δt} \nonumber\]
Ejercicio \(\PageIndex{1}\)
La velocidad de formación de Br2 es 6.0 × 10−6 mol/L/s en una reacción descrita por la siguiente ecuación iónica neta:
\[\ce{5Br- + BrO3- + 6H+ ⟶ 3Br2 + 3H2O} \nonumber\]
Escriba las ecuaciones que relacionan las tasas de consumo de los reactivos y las tasas de formación de los productos.
- Respuesta
-
\[−\dfrac{1}{5}\dfrac{Δ[\ce{Br-}]}{Δt}=−\dfrac{Δ[\ce{BrO3-}]}{Δt}=−\dfrac{1}{6}\dfrac{Δ[\ce{H+}]}{Δt}=\dfrac{1}{3}\dfrac{Δ[\ce{Br2}]}{Δt}=\dfrac{1}{3}\dfrac{Δ[\ce{H2O}]}{Δt} \nonumber\]
Ejemplo \(\PageIndex{2}\)
Expresiones para la velocidad de la reacción para la descomposición del H2O2 El gráfico de la Figura \(\PageIndex{3}\) muestra la velocidad de la descomposición de H2O2 a lo largo del tiempo:
\[\ce{2H2O2 ⟶ 2H2O + O2} \nonumber\]
Basado en estos datos, se determina que la tasa de descomposición instantánea de H2O2 en t = 11.1 h es 3.20 × 10−2 mol/L/h, es decir:
\[−\dfrac{Δ[\ce{H2O2}]}{Δt}=\mathrm{3.20×10^{−2}\:mol\: L^{−1}\:h^{−1}} \nonumber\]
¿Cuál es la tasa de producción instantánea de H2O y O2?
Solución
Usando la estequiometría de la reacción, podemos determinar que:
Por eso:
y
\[\dfrac{Δ[\ce{O2}]}{Δt}=\mathrm{1.60×10^{−2}\:mol\:L^{−1}\:h^{−1}} \nonumber \]
Ejercicio \(\PageIndex{2}\)
Si la tasa de descomposición de amoníaco, NH3, a 1150 K es 2.10 × 10−6 mol/L/s, cuál es la tasa de producción de nitrógeno e hidrógeno?
- Respuesta
-
1.05 × 10−6 mol/L/s, N2 and 3.15 × 10−6 mol/L/s, H2.
Resumen
La velocidad de una reacción se puede expresar en términos de la disminución en la cantidad de un reactivo o el aumento en la cantidad de un producto por unidad de tiempo. Las relaciones entre diferentes expresiones de velocidad para una reacción dada se derivan directamente de los coeficientes estequiométricos de la ecuación que representa la reacción.
Glosario
- tasa promedio
- velocidad de una reacción química calculada como la proporción de un cambio medido en la cantidad o concentración de sustancia al intervalo de tiempo durante el cual ocurrió el cambio
- tasa inicial
- velocidad instantánea de una reacción química en t = 0 s (inmediatamente después de que la reacción haya comenzado)
- tasa instantánea
- velocidad de una reacción química en cualquier instante en el tiempo, determinada por la pendiente de la línea tangencial a un gráfico de concentración en función del tiempo
- tasa de reacción
- medida de la velocidad a la que ocurre una reacción química
- tasa de expresión
- Representación matemática que relaciona la velocidad de la reacción con los cambios en la cantidad, concentración o presión del reactivo o especie del producto por unidad de tiempo.
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


