1: Espectroscopia coherente y polarización no lineal
- Page ID
- 73695
Se tratará específicamente de la descripción de la espectroscopia no lineal coherente, que es el término utilizado para describir el caso en el que uno o más campos de entrada actúan coherentemente sobre los dipolos de la muestra para generar una polarización oscilante macroscópica. Esta polarización actúa como fuente para irradiar una señal que detectamos en una dirección bien definida. Esta clase incluye experimentos como sondas de bombeo, rejillas transitorias, ecos de fotones y métodos Raman coherentes. Sin embargo, comprender estos experimentos permite generalizar rápidamente a otras técnicas.
| Detección: | Coherente | Espontánea |
| \[ I_{coherent}\propto|\sum_i\mu_i|^2\nonumber\] | \[ I_{spont}\propto\sum_i|\mu_i|^2\nonumber\] | |
| Lineal |
Absorción
|
Fluorescencia, fosforescencia, Raman y dispersión de luz
|
| No lineal |
Absorción transitoria bomba-sonda, ecos de fotones, rejillas transitorias, CARS, dispersión Raman impulsiva |
Espectroscopia no lineal detectada por fluorescencia, es decir, bombeo de emisión estimulada, cambio de Stokes dependiente del tiempo |
Se emiten señales espontáneas y coherentes desde todas las muestras, sin embargo, la amplitud relativa de las dos depende de la escala de tiempo de desfase dentro de la muestra. Para las transiciones electrónicas en las que la desfase suele ser mucho más rápida que la vida útil radiativa, la emisión espontánea es el proceso de emisión dominante. Para el caso de transiciones vibracionales donde la relajación no radiativa es típicamente un proceso de picosegundos y la relajación radiativa es un proceso µs o más largo, no se observa emisión espontánea. La descripción de espectroscopias coherentes no lineales se basa en el cálculo de la polarización, P. La polarización es un momento dipolo colectivo macroscópico por unidad de volumen, y para un sistema molecular se expresa como una suma sobre el desplazamiento de todas las cargas para todas las moléculas que son interrogadas por la luz.
Suma sobre moléculas:
\[\bar P (\bar r) = \sum_m \bar \mu_m \delta ( \bar r - \bar R_m) \]
Suma sobre cargas en moléculas:
\[\bar \mu_m \equiv \sum_{\alpha} q_{m\alpha} (\bar r_{m\alpha} - \bar R_m) \]
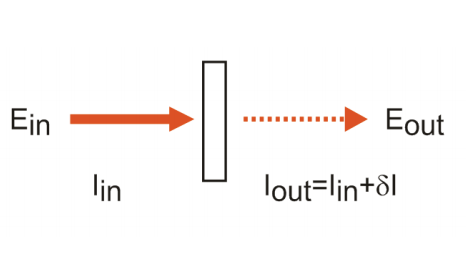
En espectroscopias coherentes, los campos de entrada E actúan para crear una distribución de carga macroscópica, coherentemente oscilante.
\[\bar P(\omega) = \chi \bar E (\omega) \]
según lo dictado por la susceptibilidad de la muestra. La polarización actúa como fuente para irradiar un nuevo campo electromagnético, al que denominamos la señal\(\bar E_{sig}\). (Recuerda que una carga acelerada irradia un campo eléctrico). En la aproximación del dipolo eléctrico, la polarización es un término en las densidades de corriente y carga que pones en las ecuaciones de Maxwell.
De nuestra descripción anterior de ondas electromagnéticas que se propagan libremente, la ecuación de onda para una onda transversal, plana era
\[\bar \nabla^2 \bar E(\bar r, t) - \frac{1}{c^2}\frac{\partial^2\bar E(\bar r, t)}{\partial t^2} = 0\]
lo que dio una solución para un campo oscilante sinusoidal con frecuencia ω propagándose en la dirección del detector de ondas k. En el presente caso, la polarización actúa como fuente − una carga acelerada − y podemos escribir
\[\bar \nabla^2 \bar E(\bar r, t) - \frac{1}{c^2}\frac{\partial^2\bar E(\bar r, t)}{\partial t^2} = \frac{4\pi}{c^2}\frac{\partial^2\bar P(\bar r, t)}{\partial t^2}\]
La polarización puede ser descrita por soluciones de la forma
\[\bar P (\bar r,t) = P(t)exp(i \bar k_{sig}' \cdot \bar r -i\omega_{sig}t) + c.c.\]
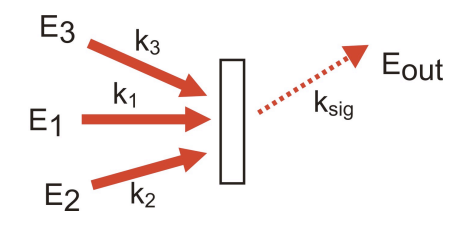
Como discutiremos más adelante, el vector de onda y la frecuencia de la polarización dependen de la frecuencia y el vector de onda de los campos incidentes.
\[\bar k_{sig} = \sum_n\pm \bar k_n\]
\[\omega_{sig} = \sum_n\pm \omega_n\]
Estas relaciones imponen impulso y conservación de energía para el problema. La polarización oscilante irradia un campo de señal coherente\(\bar E_{sig}\), en una dirección coincidente de vector de onda\(\bar k_{sig}\). Aunque un solo dipolo irradia como una distribución de campo sinθ relativa al desplazamiento de la carga, 1 para un conjunto de dipolos que han sido impulsados coherentemente por campos externos, P viene dado por (2.6) y la radiación del conjunto solo se suma constructivamente a lo largo \(\bar k_{sig}\). Para el campo radiado obtenemos
\[\bar E_{sig} (\bar r,t) = E_{sig}(\bar r,t)exp(i \bar k_{sig} \cdot \bar r -i\omega_{sig}t) + c.c.\]
Esta solución proviene de resolver (2.5) para una muestra delgada de longitud l, para lo cual la amplitud de la señal radiada crece y se vuelve direccional a medida que se propaga a través de la muestra. La señal emitida
\[\bar E_{sig}(t) = i\frac{2\pi\omega_s}{nc}l \bar P(t)sinc(\frac{\Delta kl}{2})e^{i\Delta kl/2} \]
Aquí observamos que la polarización oscilante es proporcional al campo de señal, aunque existe un desplazamiento de fase π/2 entre los dos\(\bar E_{sig}\propto i \bar P\), pues en la muestra la polarización está relacionada con el gradiente del campo. Δk es el desajuste onda-vector entre el vector de onda de la polarización\(\bar k_{sig}'\) y el campo radiado\(\bar k_{sig}\), que discutiremos más adelante.
Para el propósito de nuestro trabajo, obtenemos la polarización a partir del valor de expectativa del operador dipolo
\[\bar P(t) \Rightarrow \bar{\mu(t)}\]
El tratamiento que utilizaremos para la espectroscopia es semi-clásico, y sigue el formalismo que fue popularizado por Mukamel. 2 Como antes, nuestro hamiltoniano generalmente puede escribirse como
\[H = H_0 + V(t)\]
donde el sistema de materiales es descrito por H 0 y tratado cuántico mecánicamente, y los campos electromagnéticos V (t) son tratados clásicamente y toman la forma estándar
\[V(t)=-\bar \mu \cdot \bar E\]
Los campos sólo actúan para impulsar transiciones entre estados cuánticos del sistema. Tomamos que la interacción con los campos sea lo suficientemente débil como para poder tratar el problema con la teoría de la perturbación. Así, se utilizará la teoría de perturbación de orden n para describir la señal no lineal derivada de la interacción con n campos electromagnéticos.
- El patrón de radiación en el campo lejano para el campo eléctrico emitido por un dipolo alineado a lo largo del eje z es
\[E(r,\theta,\phi,t)=-\frac{p_0k^2}{4\pi\epsilon_0}\frac{\sin \theta}{r}\sin{(k \cdot r - \omega t)}\]
(escrito en coordenadas esféricas). Ver Jackson, Electrodinámica Clásica. - S. Mukamel, Principios de Espectroscopia Óptica No Lineal. (Oxford University Press, Nueva York, 1995).