1.1: Espectroscopia de Absorción Lineal

La absorción es el ejemplo más simple de una espectroscopia coherente. En la imagen semi-clásica, la polarización inducida por el campo electromagnético irradia un campo de señal que está desfasado con la luz transmitida. Para describir esto, toda la información relevante está en\(R(t)\) o\(\chi(\omega)\).

\[\bar P(t)=\int\limits_0^{\infty} d\tau R(\tau)E(t-\tau)\]

\[\bar P(\omega)=\chi(\omega) \bar E(\omega)\]

Comencemos con una descripción del espectro de absorción en el dominio de la frecuencia, que anteriormente encontramos que era proporcional a la parte imaginaria de la susceptibilidad,\(\chi′′\). ¹ Consideramos un campo monocromático incidente en la muestra que impulsa resonantemente dipolos en la muestra para crear una polarización, que posteriormente re-irradia un campo de señal (decaimiento de inducción libre). Para un campo de entrada, las condiciones de conservación de energía y momento lo dictan\(ω_{in} =ω_{sig}\) y\(k_{in} = k_{sig}\), es decir, un campo de señal de la misma frecuencia se propaga en la dirección del campo de excitación transmitido.

Figura\(\PageIndex{1}\): Absorción lineal con la señal propagándose en la misma dirección que la luz incidente.

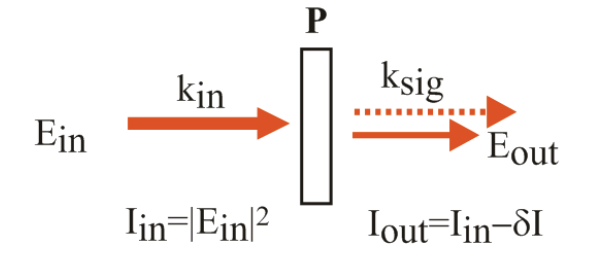
En la práctica, se mide un espectro de absorción caracterizando la disminución de transmisión dependiente de la frecuencia al sumar la muestra\(A = −\log I_{out}/I_{in}\). Para el caso perturbador, tomemos que el cambio de intensidad\(\delta I = I_{in} − I_{out}\) sea pequeño, para que\(A \approx \delta I\) y\(I_{in} \approx I_{out}\). Luego podemos escribir la intensidad medida después de la muestra como

\[\begin{align*} I_{out} &= |E_{out} + E_{sig}|^2 \\[4pt] &= |E_{out} + (iP)|^2 \\[4pt] &= |E_{out}+i\chi E_{in}|^2 \\[4pt] &\approx |E_{in} + i\chi E_{in}|^2 \\[4pt] &= |E_{in}|^2|1+i(\chi' + i\chi'')|^2 \\[4pt] &= I_{in}(1-2\chi''+\cdots) \\[4pt] \Rightarrow I_{out} &= I_{in}-\delta I \end{align*}\]

Aquí hemos hecho uso de la suposición de que\(|E_{in}| \gg |\chi| \). Vemos que como resultado del desplazamiento de fase entre la polarización y el campo radiado al que la absorbancia es proporcional\(\chi'' : \delta I = 2\chi'' I_{in} \).

Un enfoque de absorción en el dominio del tiempo se basa en la ecuación (2.1.1) y debe recuperar las relaciones con la función de autocorrelación dipolo que discutimos anteriormente. Igualando\(\bar P(t)\) con\(\bar {\mu(t)}\), podemos calcular la polarización en la imagen de la matriz de densidad como

\[\bar P(t) = Tr\left(\mu_I(t)\rho_I^{(1)}(t)\right) \]

donde la expansión de primer orden de la matriz de densidad es

\[\rho_I^{(1)}=-\frac{i}{\hbar}\int\limits_{-\infty}^{t} dt_1[V_I(t_1),\rho_{eq}]\]

Sustituyendo la eq. (2.13) encontramos

\[\begin{align*} \bar P(t) &= Tr\left(\mu_I(t)\frac{i}{\hbar}\int\limits_{-\infty}^{t} dt'[-\mu_I(t')E(t'),\rho_{eq}]\right) \\[4pt] &= -\frac{i}{\hbar}\int\limits_{-\infty}^{t} dt'E(t')Tr\left(\mu_I(t)\left[\mu_I(t'),\rho_{eq}\right]\right) \\[4pt] &= +\frac{i}{\hbar}\int\limits_{0}^{\infty} d\tau E(t-\tau ) Tr\left(\left[\mu_I(\tau),\mu_I(0)\right]\rho_{eq}\right) \end{align*}\]

En la última línea, cambiamos las variables al intervalo de tiempo\(\tau=t-t'\), y hicimos uso de la identidad\(\left[A,\left[B,C\right]\right] = \left[\left[A,B\right],C\right]\). Ahora comparando con la Eq. (2.1.1), vemos, como se esperaba

\[R(\tau)=\frac{i}{\hbar}\theta(\tau)Tr\left(\left[\mu_I(\tau),\mu_I(0)\right]\rho_{eq}\right)\]

Entonces la función de respuesta lineal es la suma de dos funciones de correlación, o más precisamente, la parte imaginaria de la función de correlación dipolo.

\[R(\tau)=\frac{i}{\hbar}\theta(\tau)\left(C(\tau)-C^*(\tau)\right)\]

\[C(\tau)=Tr\left(\mu_I(\tau)\mu_I(0)\rho_{eq}\right) \nonumber\]

\[C^*(\tau)=Tr\left(\mu_I(\tau)\rho_{eq}\mu_I(0)\right) \]

Además, como cabría esperar, cuando utilizamos un potencial impulsor impulsivo para inducir una caída de inducción libre (es decir,\(E(t-\tau)=E_0\delta(t-\tau)\)), la polarización es directamente proporcional a la función de respuesta, que puede ser transformada de Fourier para obtener la forma de línea de absorción.

1. Recuerde las siguientes relaciones de la susceptibilidad con la constante dieléctrica compleja\(\epsilon(\omega)\), el índice de refracción\(n(\omega)\) y el coeficiente de absorción\(\kappa(\omega)\):

\[\epsilon(\omega)=1+4\pi\chi(\omega) \nonumber\]

\[\sqrt{\epsilon(\omega)}=\tilde n(\omega)= n(\omega)+i\kappa(\omega) \nonumber\]