2.5: Espectroscopia no lineal de tercer orden

Ahora veamos ejemplos de teoría de perturbación diagramática aplicada a la espectroscopia no lineal de tercer orden. Las no linealidades de tercer orden describen la mayoría de los experimentos no lineales coherentes que se utilizan, incluyendo experimentos de bomba-sonda, rejillas transitorias, ecos de fotones, espectroscopía Raman coherente anti-Stokes (CARS) y mezcla degenerada de cuatro ondas (4WM). Estos experimentos son descritos por algunas o la totalidad de las ocho funciones de correlación que contribuyen a\(R^{(3)}\):

\[R^{(3)}=\left(\frac{i}{\hbar}\right)^3\sum_{\alpha=1}^4\left[R_\alpha - R^*_\alpha\right] \label{3.5.1}\]

Los diagramas y la respuesta correspondiente primero requieren que especifiquemos los estados propios del sistema. El caso más simple, que nos permite discutir una serie de ejemplos de espectroscopia de tercer orden es un sistema de dos niveles. Escribamos los diagramas y las funciones de correlación para un sistema de dos niveles comenzando en\(\rho_{aa}\), donde el operador dipolo se empareja\(|b\rangle\) y\(|a\rangle\).

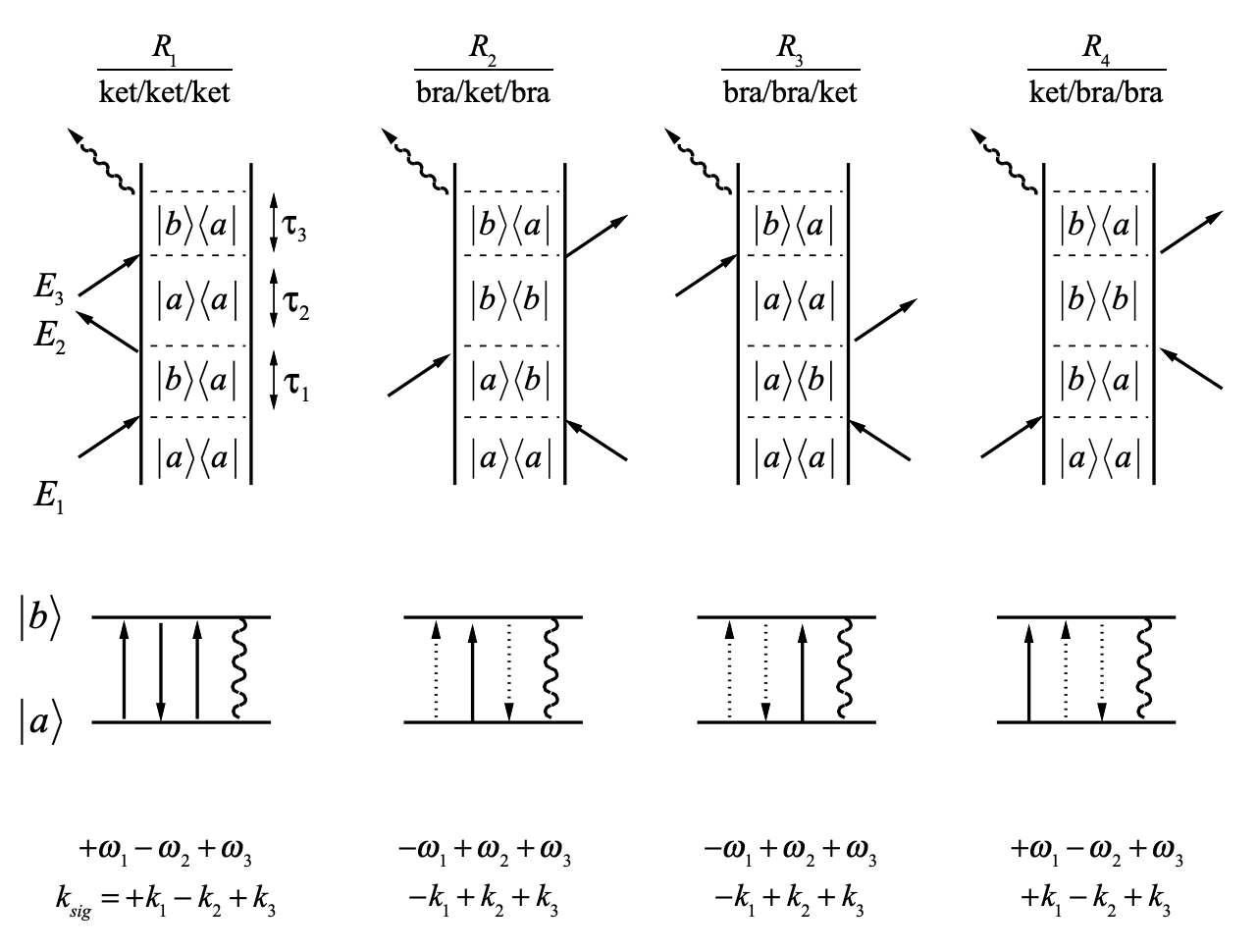
Como ejemplo, escribamos la función de correlación para _R2 obtenida del diagrama anterior. Este término es importante para comprender los experimentos de eco de fotones y contribuye a los experimentos de mezcla de cuatro ondas de bombeo y sonda degenerada.

\[\begin{aligned} R_{2} &=(-1)^{2} p_{a}\left(\mu_{b a}^{*}\right)\left[e^{-i \omega_{a b} \tau_{1}-\Gamma_{a b} \tau_{1}}\right]\left(\mu_{b a}\right)\left(e^{\cancel{-i \omega_{b b} \tau_{2}}-\Gamma_{b b} \tau_{2}}\right)\left(\mu_{a b}^{*}\right)\left[e^{-i \omega_{b a} \tau_{3}-\Gamma_{b a} \tau_{3}}\right]\left(\mu_{a b}\right) \\ &=p_{a}\left|\mu_{a b}\right|^{4} \exp \left[-i \omega_{b a}\left(\tau_{3}-\tau_{1}\right)-\Gamma_{b a}\left(\tau_{1}+\tau_{3}\right)-\Gamma_{b b}\left(\tau_{2}\right)\right] \end{aligned} \label{3.5.2}\]

Los diagramas muestran cómo las contribuciones del campo de entrada dictan la frecuencia del campo de señal y el evector de ondas. Reconociendo la dependencia de\(E_{sig}^{(3)} \sim P^{(3)} \sim R_2(E_1E_2E_3) \), estos se obtienen del producto de las contribuciones de campo incidentes

\[\begin{aligned} \bar E_1 \bar E_2 \bar E_3 &= \left(E_1^*e^{+i\omega_1t-i\bar k_1\cdot\bar r}\right)\left(E_2e^{-i\omega_2t+i\bar k_2\cdot r}\right)\left(E_3e^{+i\omega_3t-i\bar k_3\cdot\bar r_3}\right) \\ &\implies E_1^*E_2E_3e^{-\omega_{sig}t+i\bar k_{sig}\cdot\bar r} \end{aligned} \label{3.5.3}\]

\[\begin{aligned} \therefore \omega_{sig2} &= -\omega_1 + \omega_2 + \omega_3 \\ k_{sig2} &= -\bar k_1 +\bar k_2 +\bar k_3 \end{aligned} \label{3.5.4}\]

Ahora, comparemos esto con la respuesta obtenida de R ₄. Estos obtenemos

\[R_4=p_a|\mu_{ab}|^4exp\left[-i\omega_{ba}(\tau_3+\tau_1)-\Gamma_{ba}(\tau_1+\tau_3)-\Gamma_{bb}(\tau_2)\right] \label{3.5.5}\]

\[\begin{aligned} \omega_{sig4} &= +\omega_1 - \omega_2 + \omega_3 \\ k_{sig4} &= +\bar k_1 -\bar k_2 +\bar k_3 \end{aligned} \label{3.5.6}\]

_{Obsérvese que los términos R2 y R4 son idénticos, a excepción de la fase adquirida durante el periodo inicial:\(exp[i\phi]=exp[\pm i\omega_{ba}\tau_1]\).} El término R ₂ evoluciona en coherencias conjugadas durante los\(\tau_3\) periodos\(\tau_1\) y, mientras que el término R ₄ evoluciona en el mismo estado de coherencia durante ambos periodos:

	Coherencias en\(\tau_1\) y\(\tau_3\)	Fase adquirida en\(\tau_1\) y\(\tau_3\)
R 4	\(|b\rangle\langle a| \rightarrow |b\rangle\langle a| \)	\( e^{-i\omega_{ba}(\tau_1+\tau_3)} \)
R 2	\(|a\rangle\langle b| \rightarrow |b\rangle\langle a|\)	\( e^{-i\omega_{ba}(\tau_1-\tau_3)} \)

El término R ₂ tiene la propiedad de inversión de tiempo: la fase adquirida durante\(\tau_1\) se invierte en\(\tau_3\). Por esa razón el término se llama “rephasing”. Las señales de refase se seleccionan en experimentos de eco de fotones y se utilizan para distinguir los mecanismos de ampliación de línea y estudiar la difusión espectral. Para R ₄, la fase adquirida continuamente en\(\tau_1\) y\(\tau_3\), y este término se llama “no rephasing”. El análisis de R ₁ y R ₃ revela que estos términos son no-rephasing y rephasing, respectivamente.

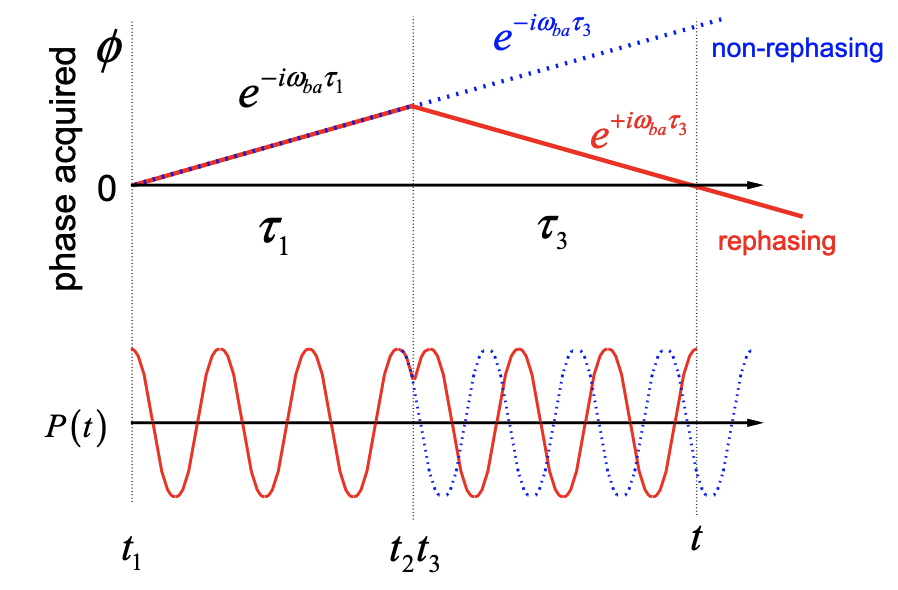
Para el presente caso de una espectroscopia de tercer orden aplicada a un sistema de dos niveles, observamos que las dos funciones de refase _R2 y _R3 tienen la misma frecuencia de emisión y evector de ondas, y por lo tanto ambas contribuirían por igual a una geometría de detección dada. Los dos términos difieren en qué estado poblacional se propagan durante la\(\tau_2\) variable. De igual manera, las funciones de no refase _R1 y _R4 tienen cada una la misma frecuencia de emisión y evector de onda, pero difieren según la\(\tau_2\) población. Para las transiciones entre más de dos estados del sistema, estos términos podrían estar separados por frecuencia o por ondas (ver apéndice). Dado que el par de refase _R2 y _R3 contribuyen por igual a una señal dispersa en la dirección −k ₁ + k ₂ + k ₃, también se les conoce como\(S_I\). El par de no refase R1 y R4 se dispersan en la dirección + k ₁ − k ₂ + k ₃ y se etiquetan como\(S_{II}\).

Nuestros hallazgos para las cuatro funciones de correlación independientes se resumen a continuación.

			\(\omega_{sig}\)	\(k_{sig}\)	\(\tau_2\)población
\(S_I\)	reescalonamiento	R 2	\(-\omega_1 +\omega_2 +\omega_3\)	\(-k_1 +k_2 +k_3\)	estado excitado
		R 3	\(-\omega_1 +\omega_2 +\omega_3\)	\(-k_1 +k_2 +k_3\)	estado de tierra
\(S_{II}\)	no reescalonamiento	R 1	\(+\omega_1 -\omega_2 +\omega_3\)	\(+k_1 -k_2 +k_3\)	estado de tierra
		R 4	\(+\omega_1 -\omega_2 +\omega_3\)	\(+k_1 -k_2 +k_3\)	estado excitado