4.4: ¿Cómo se pueden caracterizar las fluctuaciones y la difusión espectral?

La capacidad de refase del experimento de eco de fotones proporciona una manera de caracterizar la memoria de la frecuencia de transición de brecha de energía inicialmente excitada por el primer pulso. Para una forma de línea estática no homogénea, se conserva la memoria perfecta de las frecuencias de transición a través del experimento, mientras que el ensanchamiento homogéneo implica una desfase extremadamente rápida. Entonces, examinemos primero la polarización para un experimento de eco de fotones de dos pulsos en un sistema con ensanchamiento homogéneo e inhomogéneo variando\(\Delta/\Gamma_{eg}\). Trazando la polarización como proporcional a la respuesta en eq. (5.3.7):

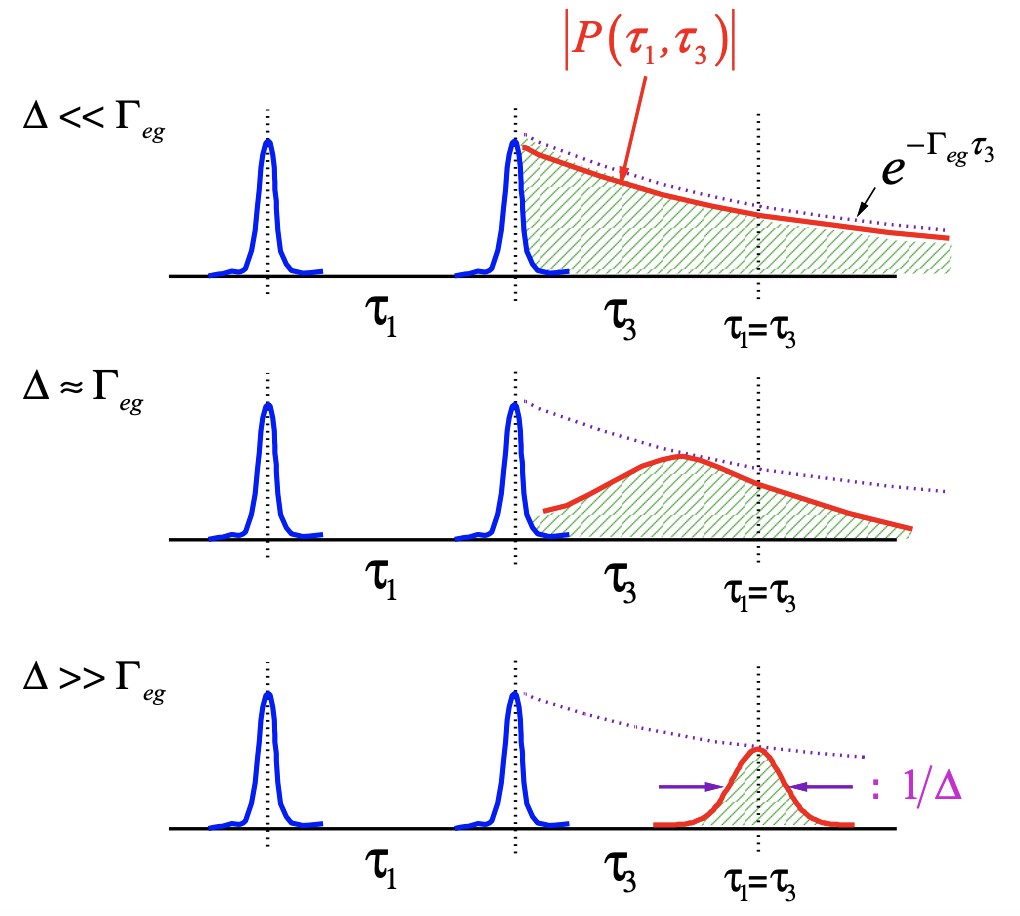
Vemos que siguiendo el tercer pulso, la polarización (línea roja) se amortigua\(\tau_3\) durante la desfase homogénea a una velocidad\(\Gamma_{eg}\), independientemente de Δ. Sin embargo, en el caso no homogéneo\(\Delta\gt\gt\Gamma_{eg}\), cualquier inhomogeneidad se vuelve a poner en fase\(\tau_1=\tau_3\). La forma de este eco es un Gaussiano con ancho ~ 1/ Δ. La forma de la polarización de eco es una competencia entre la amortiguación homogénea y la refase no homogénea.

Normalmente, se detecta la intensidad integrada del campo de eco radiado. Ajuste del retardo de pulso\(\tau_1=\tau\),

\[S(\tau)\propto\int_0^{\infty}d\tau_3|P^{(3)}(\tau,\tau_3)|^2 \label{5.4.1}\]

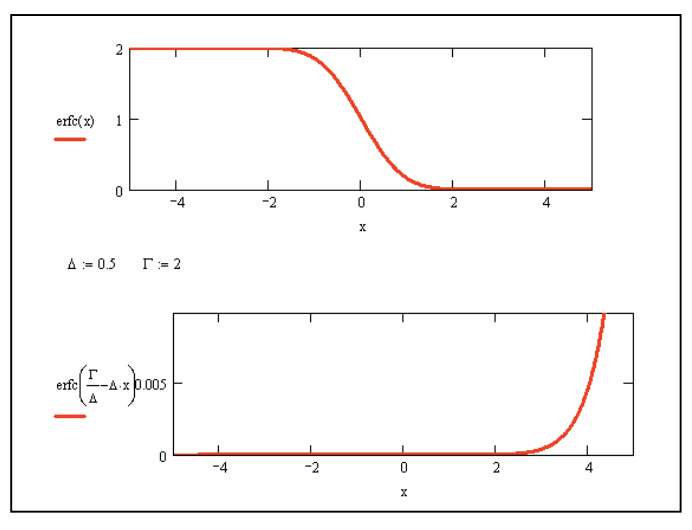
\[S(\tau)=exp\left(-4\Gamma_{eg}\tau-\frac{\Gamma_{eg}^2}{\Delta^2}\right)\cdot erfc\left(-\Delta\tau+\frac{\Gamma_{eg}}{\Delta}\right) \label{5.4.2}\]

donde\(erfc(x)=1-erf(x)\) está la función de error complementaria. Para los límites homogéneos e inhomogéneos de esta expresión encontramos

\[\Delta \lt\lt \Gamma_{eg} \Rightarrow S(\tau)\propto e^{-2\Gamma_{eg}\tau} \label{5.4.3}\]

\[\Delta \gt\gt \Gamma_{eg} \Rightarrow S(\tau)\propto e^{-4\Gamma_{eg}\tau} \label{5.4.4}\]

En cualquiera de los dos límites, la inhomogeneidad se elimina de la decaimiento medido. En el caso intermedio, observamos que el término principal en eq. (5.4.2) decae mientras que el segundo término se eleva con el tiempo. Esto refleja la competencia entre el amortiguamiento homogéneo y el reajuste no homogéneo. Como resultado, para el caso intermedio\((\Delta \approx \Gamma_{ab})\) encontramos que la señal integrada\(S(\tau)\) tiene una señal máxima para\(\tau\gt 0\).

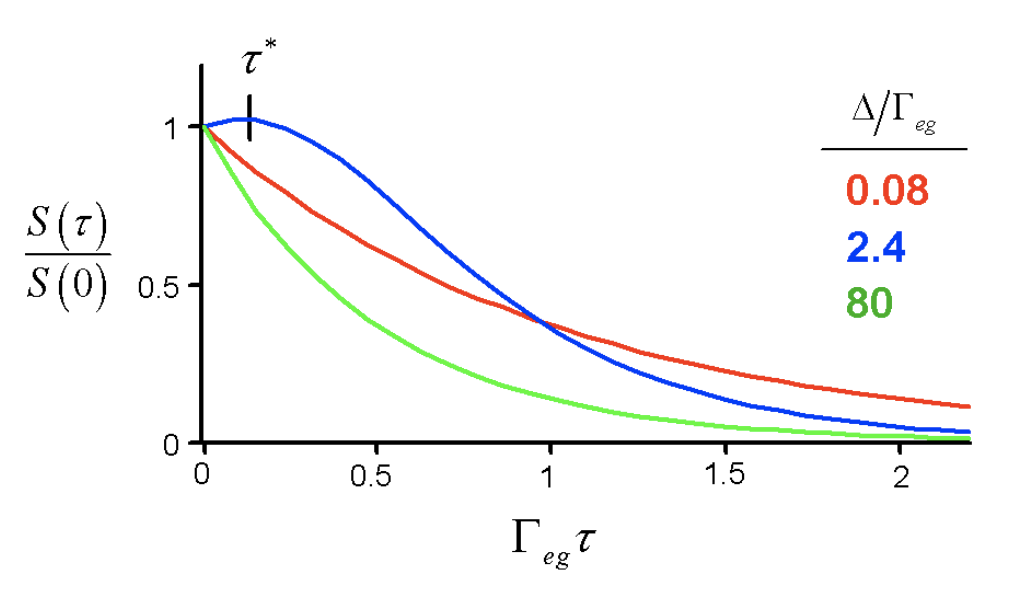
El retardo de la señal máxima,\(\tau^*\), se conoce como el desplazamiento de pico. La observación de un cambio de pico es una indicación de que existe una capacidad imperfecta para reformular. La desfase homogénea, es decir, fluctuaciones rápidas en la escala de tiempo de\(\tau\), están actuando para revolver la memoria de la fase de la coherencia creada inicialmente por el primer pulso.

De la misma manera, la difusión espectral (procesos que modulan aleatoriamente la brecha de energía en escalas de tiempo iguales o mayores que\(\tau\)) aleatoriza la fase. Destruye la capacidad de que se forme un eco refasando. Para caracterizar estos procesos a través de una función de correlación de brecha de energía, podemos realizar un experimento de eco de fotones de tres pulsos. El experimento de tres pulsos introduce un tiempo de espera\(\tau_2\) entre los dos períodos de coherencia, que actúa para definir una velocidad de obturación variable para el experimento. El sistema evoluciona como población durante este periodo, por lo que nominalmente no hay fase adquirida. Podemos ilustrar esto a través de una analogía de lentes:

Analogía de lentes: Para una distribución no homogénea de osciladores con diferentes frecuencias, definimos la fase adquirida durante un periodo de tiempo a través de\(e^{i\phi}=e^{i(\delta\omega_i t)}\)

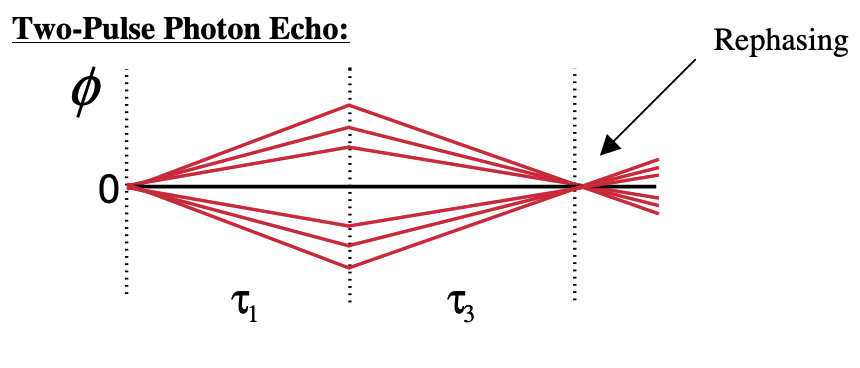
Ya que estamos en un estado poblacional durante\(\tau_2\), no hay evolución de fase. Ahora a esta imagen podemos agregar difusión espectral como una modulación aleatoria más lenta de la fase adquirida durante todos los periodos de tiempo. Si el sistema puede difundirse espectralmente durante\(\tau_2\), esto degrada la capacidad del sistema de refase y la formación de eco disminuye.

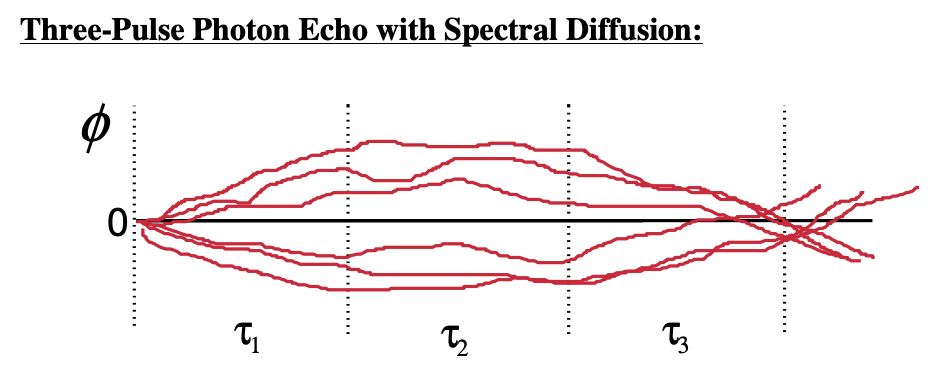
Dado que la difusión espectral destruye la refase, el sistema aparece cada vez más “homogéneo” a medida\(\tau_2\) que se incrementa. Experimentalmente, se observa cómo el cambio de pico del eco integrado cambia con el tiempo de espera\(\tau_2\). Se observará para cambiar hacia\(\tau^*=0\) como una función de\(\tau_2\).

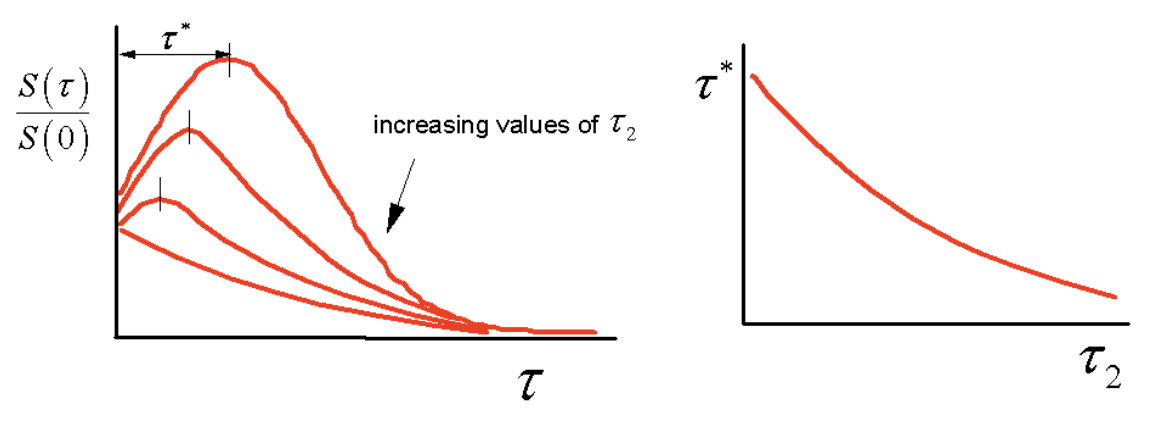
De hecho, se puede mostrar que el cambio de pico con\(\tau_2\) decae con una forma dada por la función de correlación para las interacciones sistema-baño:

\[\tau^*(\tau_2)\propto C_{eg}(\tau) \label{5.4.5}\]

Usando la función lineshape para el modelo estocástico\(g(t)=\Delta^2\tau_c^2\left[exp(-t/\tau_c)+t/\tau_c-1\right]\), se puede ver que por tiempos\(\tau_2\gt\tau_c\),

\[\tau^*(\tau_2)\propto exp(-\tau_2/\tau_c)\Rightarrow \left\langle\delta\omega_{eg}(\tau)\delta\omega_{eg}(0)\right\rangle \label{5.4.6}\]

Por lo tanto, las mediciones de desplazamiento de pico de eco son un método general para determinar la forma a\(C_{eg}(\tau)\) o\(C_{eg}''(\omega)\) o\(\rho(\omega)\). La escala de tiempo de medición está limitada solo por la vida de la población.