5.2: Espectroscopia 2D desde Respuesta de Tercer Orden

Última actualización
Guardar como PDF

Page ID: 73651

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Estos ejemplos indican que los experimentos de bomba-sonda de banda estrecha pueden usarse para construir espectros 2D, por lo que de hecho la respuesta no lineal de tercer orden debería describir espectros 2D. Para describir estos espectros, podemos pensar en la excitación como un proceso de tercer orden derivado de una secuencia de interacciones con los estados propios del sistema. Por ejemplo, tomando nuestro ejemplo inicial con tres niveles, uno de los factores contribuyentes es de la forma _R2:

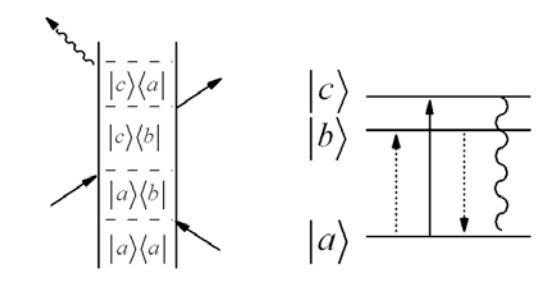
Ajuste\(\tau_2=0\) y descuidando la amortiguación, la función de respuesta es

\[R_2(\tau_1,\tau_3)=p_a|\mu_{ab}|^2|\mu_{ac}|^2e^{-i\omega_{ba}\tau_1-i\omega_{ca}\tau_3} \label{7.1}\]

El comportamiento del dominio del tiempo describe la evolución de un estado coherente a otro, impulsado por los campos de luz:

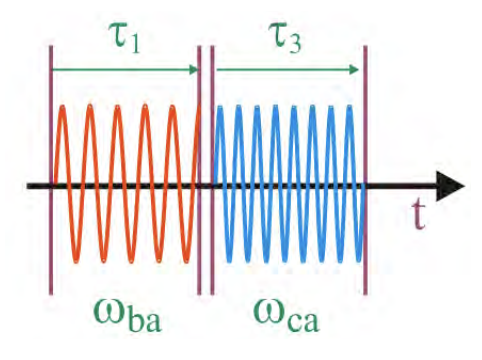
Una descripción más intuitiva se encuentra en el dominio de la frecuencia, la cual obtuvimos mediante la transformación de Fourier eq. (7.1):

\[\begin{aligned} \tilde R_2(\omega_1,\omega_3) &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{i\omega_1\tau_1+i\omega_3\tau_3}R_2(\tau_1,\tau_3)d\tau_1d\tau_3 \\ &=p_a|\mu_{ab}|^2|\mu_{ac}|^2\left\langle\delta(\omega_3-\omega_{ca})\delta(\omega_1-\omega_{ba})\right\rangle \\ &\equiv p_a|\mu_{ab}|^2|\mu_{ac}|^2P(\omega_3,\tau_2;\omega_1) \end{aligned} \label{7.2}\]

La función P se parece a la covarianza\(\langle xy \rangle\) que describe la correlación de dos variables x e y. De hecho, P es una función de probabilidad conjunta que describe la probabilidad de excitar el sistema\(\omega_{ba}\) y observar el sistema en\(\omega_{ca}\) (después de esperar un tiempo\(\tau_2\)). En particular, este diagrama describe el pico cruzado en la parte superior izquierda del ejemplo inicial que discutimos.