5.4: Caracterización de acoplamientos en espectros 2D
- Page ID
- 73680
Una de las características únicas de la espectroscopia 2D es la capacidad de caracterizar acoplamientos moleculares 1. Esto permite comprender las relaciones microscópicas entre diferentes objetos, y con el conocimiento del mecanismo de interacción, determinar la estructura o revelar la dinámica del sistema. Para entender cómo los espectros 2D reportan interacciones moleculares, discutiremos la espectroscopia usando un modelo para dos grados de libertad acoplados electrónicos o vibracionales. Dado que el espectro 2D informa sobre los estados propios del sistema acoplado, comprender el acoplamiento entre estados microscópicos requiere un modelo para los autoestados en base a las coordenadas interactuantes de interés. La espectroscopia lineal tradicional no proporciona suficientes restricciones para determinar de manera única estas variables, pero la espectroscopia 2D proporciona esta información a través de una caracterización de autoestados de dos cuánticos.
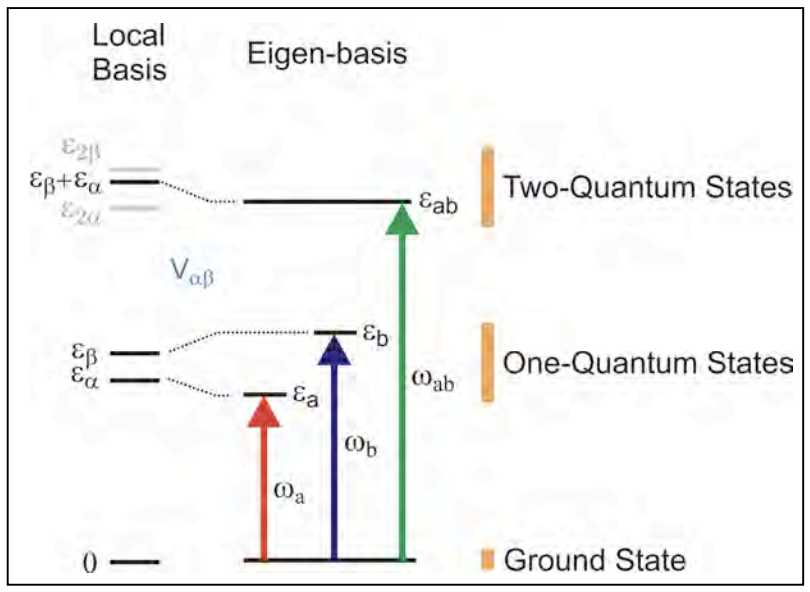
Dado que se necesita menos energía para excitar una coordenada si una coordenada acoplada ya tiene energía en ella, una caracterización de la energía del modo combinado con un cuántico de excitación en cada coordenada proporciona una ruta para obtener el acoplamiento. Este principio se basa en el uso de espectroscopía molecular de armónicos y bandas combinadas para desentrañar acoplamientos anarmónicos.
El lenguaje para las diferentes variables para el hamiltoniano de dos coordenadas acopladas varía considerablemente según la disciplina. Una variedad de términos que se utilizan se resumen a continuación. Usaremos los términos subrayados.
| Sistema Hamiltoniano\(H_S\) | Base local o sitio (i, j) | Base propia (a, b) | Eigenstates de un solo cuántico | Eigenstates de dos cuánticos |
|---|---|---|---|---|
| \ (H_S\) ">
Modo local Hamiltoniano Exciton Hamiltonian |
Sitios Modos locales |
Eigenstates Estados excitones Estados deslocalizados |
Fundamental v=0-1 Estados |
Modo combinado o banda Sobresonar Estados |
El modelo para dos coordenadas acopladas puede tomar muchas formas. Prestaremos especial atención a un hamiltoniano que describe el acoplamiento entre dos modos vibracionales locales i y j acoplados a través de una interacción bilineal de fuerza J:
\[\begin{aligned} H_{vib} &= H_i+H_j+V_{i,j} \\ &=\frac{p_i^2}{2m_i}+V(q_i)+\frac{p_j^2}{2m_j}+V(q_j)+Jq_iq_j \end{aligned} \label{9.1}\]
Una forma alternativa fundida en los operadores de escalera para estados vibracionales o electrónicos es el excitón Frenkel Hamiltoniano
\[H_{vib,harmonic}\approx\hbar\omega_i\left(a_i^\dagger a_i\right)+\hbar\omega_j\left(a_j^\dagger a_j\right)+J\left(a_i^\dagger a_j+a_i a_j^\dagger\right) \label{9.2}\]
\[H_{elec}=E_ia_i^\dagger a_i+E_ja_j^\dagger a_j+\left(J_{ij}a_i^\dagger a_j+c.c\right) \label{9.3}\]
La interacción bi-lineal es la forma más simple por la cual la energía de un estado depende del otro. Se puede pensar en ello como el término líder en la expansión del acoplamiento entre los dos estados locales. Los términos de expansión de orden superior se utilizan en otra forma común, el acoplamiento anarmónico cúbico entre los modos normales de vibración
\[H_{vib}=\left(\frac{p_i^2}{2m_i}+\frac{1}{2}k_iq_i^2+\frac{1}{6}g_{iii}q_i^2\right)+\left(\frac{p_j^2}{2m_j}+\frac{1}{2}k_jq_j^2+\frac{1}{6}g_{jjj}q_j^2\right)+\left(\frac{1}{2}g_{iij}q_i^2q_j+\frac{1}{2}g_{ijj}q_iq_j^2\right) \label{9.4}\]
En el caso de la eq. (9.2), los autoestados y los valores propios de energía para los estados unicuánticos se obtienen diagonalizando la matriz 2x2
\[H_S^{(1)}=\begin{pmatrix} E_{i=1} & J \\ J & E_{j=1} \end{pmatrix} \label{9.5}\]
\(E_{i=1}\)y\(E_{j=1}\) son las energías uno-cuánticas para los modos locales\(q_i\) y\(q_j\). Estos le dan al sistema valores propios de energía
\[E_{a/b}=\Delta E \pm\left(\Delta E^2+J^2\right)^{1/2} \label{9.6}\]
\[\Delta E=\frac{1}{2}\left(E_{i=1}-E_{j=1}\right) \label{9.7}\]
\(E_a\)y se\(E_b\) pueden observar en el espectro lineal, pero no son suficientes para desentrañar las tres variables (energías de sitio\(E_iE_j\) y acoplamiento J) relevantes para el hamiltoniano; se necesita más información.
Para fines de espectroscopía 2D, el acoplamiento se codifica en los autoestados de dos cuánticos. Dado que se necesita menos energía para excitar una vibración\(|i\rangle\) si un modo acoplado\(|j\rangle\) ya tiene energía, podemos caracterizar la fuerza de interacción de los estados propios del sistema determinando la energía del modo combinado en\(E_{ab}\) relación con la suma de los fundamentos:
\[\Delta_{ab}=E_a+E_b-E_{ab} \label{9.8}\]
En esencia, con una caracterización de\(E_{ab},E_a,E_b\) uno tiene tres variables que restringen\(E_i,E_j,J\). La relación entre\(\Delta_{ab}\) y J depende del modelo.
Trabajando específicamente con la ecuación vibracional hamiltoniana (9.1), hay tres dos estados cuánticos que deben ser considerados. Expresado como estados de producto en los dos modos locales estos son\(|i,j\rangle = |20\rangle, |02\rangle,\) y\(|11\rangle\). Los valores propios de dos energías cuánticas del sistema se obtienen diagonalizando la matriz 3x3
\[ H_S^{(2)}=\begin{pmatrix} E_{i=2} & 0 & \sqrt{2}J \\ 0 & E_{j=2} & \sqrt{2}J \\ \sqrt{2}J & \sqrt{2}J & E_{i=1}+E_{j=1} \end{pmatrix} \label{9.9}\]
Aquí\(E_{i=2}\) y\(E_{j=2}\) están las dos energías cuánticas para los modos locales\(q_i\) y\(q_j\). Estos se expresan comúnmente en términos de\(\delta E_i\), el desplazamiento anarmónico de la brecha de energía i =1-2 en relación con la energía uno-cuántica i =0-1:
\[\begin{aligned} \delta E_i &= \left(E_{i=1}-E_{i=0}\right)-\left(E_{i=2}-E_{i=1}\right) \\ \delta\omega_i &= \omega_{10}^i-\omega_{21}^i \end{aligned} \label{9.10}\]
Si bien existen soluciones analíticas a la eq. (9.9), es más informativo examinar soluciones en dos límites. En el límite de acoplamiento fuerte (\(J\lt\lt\Delta E\)), uno encuentra
\[\Delta_{ab}=J \label{9.11}\]
Para vibraciones con la misma anharmonía\(\delta E\) con acoplamiento débil entre ellas (\(J\lt\lt\Delta E\)), la teoría de perturbación rinde
\[\Delta_{a b}=\delta E \frac{J^{2}}{\Delta E^{2}} \label{9.12}\]
Este resultado es similar a la solución perturbadora para osciladores débilmente acoplados de la forma dada por la ecuación (9.4)
\[\Delta_{a b}=g_{i i j}^{2}\left(\frac{4 E_{i}}{E_{j}^{2}-4 E_{i}^{2}}\right)+g_{i j j}^{2}\left(\frac{4 E_{j}}{E_{i}^{2}-4 E_{j}^{2}}\right) \label{9.13}\]
Ejemplo\(\PageIndex{1}\): \(\ce{Rh(CO)2(acac)}\)
Entonces, ¿cómo se presentan estas variables en espectros 2D? Aquí es útil usar un ejemplo específico: las vibraciones carbonílicas fuertemente acopladas de\(\ce{Rh(CO)2(acac)}\) o RDC. Para fines de espectroscopia 2D con campos infrarrojos resonantes con las transiciones carbonilo, hay seis estados cuánticos (contando el estado fundamental) que deben ser considerados. El acoplamiento entre los dos tramos de CO degenerados conduce a estados propios simétricos y antisimétricos, a los que se hace referencia más comúnmente por sus designaciones de modo normal: las vibraciones simétricas y asimétricas de estiramiento. Para n=2 vibraciones acopladas, hay n (n−1) /2 = 3 autoestados de dos cuánticos. En la designación de modo normal, estos son los primeros armónicos de los modos simétrico y asimétrico y la banda de combinación. Esto conduce a un sistema de seis niveles para los estados propios del sistema, que designamos por el número de cuantos en el tramo simétrico y asimétrico:\(|00\rangle\)\(|10\rangle\),\(|s\rangle\)\(|a\rangle\) =\(|01\rangle\),\(|2s\rangle\) =\(|20\rangle\),\(|2a\rangle\) =\(|02\rangle\), y\(|sa\rangle\) =\(|11\rangle\). Para un sistema electrónico modelo, hay cuatro niveles esenciales que deben considerarse, ya que la estadística de Fermi no permite dos electrones en un mismo estado:\(|00\rangle\),\(|10\rangle\),\(|01\rangle\), y\(|11\rangle\).
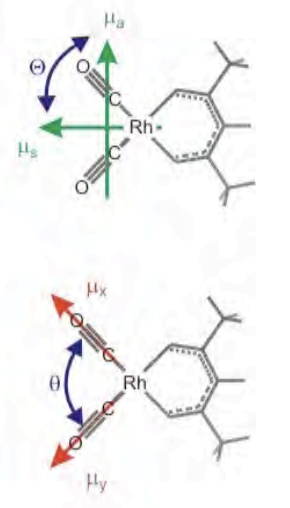
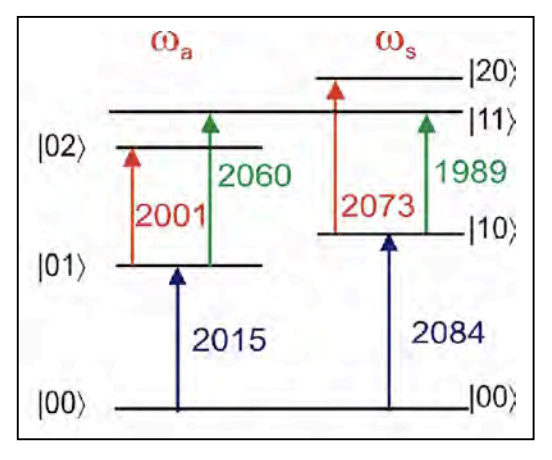
Ahora calculamos la respuesta no lineal de tercer orden para este sistema de seis niveles, asumiendo que toda la población se encuentra inicialmente en el estado básico. Describir un espectro de correlación 2D de doble resonancia o transformada de Fourier en las variables\(\omega_1\) e\(\omega_3\) incluir todos los términos relevantes para los experimentos bomba-sonda:\(-k_1 +k_2 +k_3\) (\(S_{I}\), rephasing) y\(k_1 - k_2 +k_3\) (\(S_{II}\), non-rephasing). Después de sumar muchas permutaciones de interacción usando el propagador fenomenológico, manteniendo solo dipolo permitido transiciones con ±1 cuántico, encontramos que esperamos ocho resonancias en un espectro 2D. Para el caso del espectro de refase\(S_I\)
\[\begin{aligned} S_I(\omega_1,\omega_3) &= \frac{2|\mu_{s,0}|^4}{\left[i(\omega_1+\omega_{s,0})+\Gamma_{s,0}\right]\left[i(\omega_3-\omega_{s,0})+\Gamma_{s,0}\right]} + \frac{2|\mu_{a,0}|^4}{\left[i(\omega_1+\omega_{a,0})+\Gamma_{a,0}\right]\left[i(\omega_3-\omega_{a,0})+\Gamma_{a,0}\right]} \\ &+ \frac{2|\mu_{a,0}|^2|\mu_{s,0}|^2}{\left[i(\omega_1+\omega_{s,0})+\Gamma_{s,0}\right]\left[i(\omega_3-\omega_{a,0})+\Gamma_{a,0}\right]} + \frac{2|\mu_{a,0}|^2|\mu_{s,0}|^2}{\left[i(\omega_1+\omega_{a,0})+\Gamma_{a,0}\right]\left[i(\omega_3-\omega_{s,0})+\Gamma_{b,0}\right]} \\ &- \frac{|\mu_{s,0}|^2|\mu_{2s,s}|^2}{\left[i(\omega_1+\omega_{s,0})+\Gamma_{s,0}\right]\left[i(\omega_3-\omega_{s,0}+\Delta_{s})+\Gamma_{2s,s}\right]} - \frac{|\mu_{a,0}|^2|\mu_{2a,a}|^2}{\left[i(\omega_1+\omega_{a,0})+\Gamma_{a,0}\right]\left[i(\omega_3-\omega_{a,0}+\Delta_{a})+\Gamma_{2a,a}\right]} \\ &-\frac{|\mu_{s,0}|^2|\mu_{as,s}|^2+\mu_{0,s}\mu_{a,0}\mu_{as,a}\mu_{s,as}}{\left[i(\omega_1+\omega_{s,0})+\Gamma_{s,0}\right]\left[i(\omega_3-\omega_{a,0}+\Delta_{as})+\Gamma_{as,s}\right]} - \frac{|\mu_{a,0}|^2|\mu_{as,a}|^2+\mu_{0,a}\mu_{s,0}\mu_{as,s}\mu_{a,as}}{\left[i(\omega_1+\omega_{a,0})+\Gamma_{a,0}\right]\left[i(\omega_3-\omega_{s,0}+\Delta_{as})+\Gamma_{as,a}\right]} \\ &\equiv {\bf 1+1'+2+2'+3+3'+4+4'} \end{aligned} \label{9.14}\]
Para discutir estos picos examinamos cómo aparecen en el espectro IR 2D de transformada de Fourier experimental de RDC, aquí trazados tanto en modo de absorción diferencial como en modo de valor absoluto. Observamos que hay ocho picos, etiquetados de acuerdo con los términos i eq. (9.14) de los que surgen. Cada pico especifica una secuencia de interacciones con los estados propios del sistema, con excitación en un particular\(\omega_1\) y detección dada\(\omega_3\). Observe que en la dimensión de excitación\(ω_1\) todos los picos se encuentran en una de las frecuencias fundamentales. A lo largo del eje de detección se observan\(\omega_3\) resonancias en las seis transiciones monocuánticas presentes en nuestro sistema.
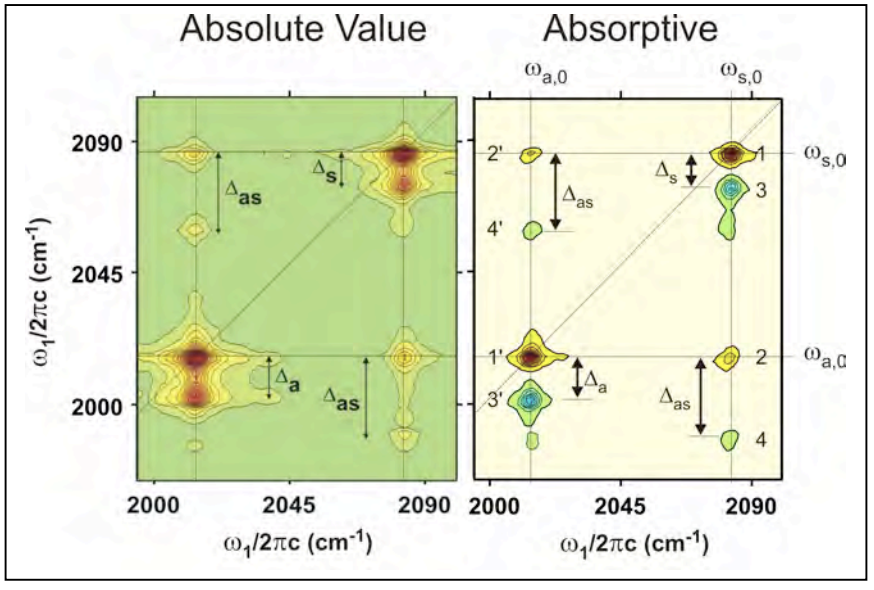
Más precisamente, hay cuatro características: dos diagonales y dos picos cruzados cada uno de los cuales se dividen en un par. Las características de pico diagonal y cruzado positivo representan la evolución en las transiciones fundamentales, mientras que las características negativas divididas surgen de la propagación en el colector de dos cuánticos. Los picos diagonales representan una secuencia de interacciones con el campo que deja la coherencia en la misma transición durante ambos periodos, donde como el pico dividido representa la promoción de lo fundamental a lo armónico durante la detección. El armónico se desplaza anarmónicamente, y por lo tanto la división entre los picos,\(\Delta_a,\Delta_s\),, da la anarmónica diagonal. Los picos cruzados surgen de la transferencia de excitación de uno fundamental a otro, mientras que el pico desplazado representa la promoción a la banda de combinación para la detección. La banda de combinación se desplaza en frecuencia debido al acoplamiento entre los dos modos, y por lo tanto la división entre los picos en las características fuera de la diagonal\(\Delta_{as}\) da la anarmonicidad fuera de la diagonal.
Observe por cada par dividido de picos, que en el límite en que la anarmónica se desvanece, los dos picos en cada característica se superpondrían. Dado que tienen signo opuesto, los picos interferirían destructivamente y desaparecerían para un sistema armónico. Esta es una manifestación de la regla de que una respuesta no lineal se desvanece para un sistema armónico. Entonces, de hecho, un espectro 2D tendrá firmas de cualquier tipo de interacciones vibracionales que conduzcan a una interferencia imperfecta entre estas dos contribuciones. La no linealidad del momento dipolar de transición conducirá a la cancelación imperfecta de los picos a nivel de amplitud, y el acoplamiento no lineal con un baño conducirá a diferentes formas de línea para las dos características.
Con una asignación de los picos en el espectro, se han mapeado las energías de los autoestados del sistema de uno y dos cuánticos. Estos valores propios actúan para limitar cualquier modelo que se utilizará para interpretar el sistema. Ahora se puede evaluar cómo los modelos para las vibraciones acopladas coinciden con los datos. Por ejemplo, al ajustar el espectro RDC al Hamiltoniano en eq. (9.1) para dos modos locales anarmónicos acoplados con un potencial de la forma\(V\left(q_{i}\right)=\frac{1}{2} k_{i} q_{i}^{2}+\frac{1}{6} g_{i i i} q_{i}^{3}\), obtenemos\(\hbar \omega_{10}^{i}=\hbar \omega_{10}^{j}=2074 \mathrm{~cm}^{-1}\),\(J_{i j}=35 \mathrm{~cm}^{-1}\), y\(g_{iii} = g_{jjj} = 172 \mathrm{~cm}^{-1}\). Alternativamente, podemos describir el espectro a través de la ecuación (9.4) como modos normales simétricos y asimétricos con anharmonía diagonal y fuera de diagonal. Esto lleva a\(\hbar \omega_{10}^{a}=2038 \mathrm{~cm}^{-1}\),\(\hbar \omega_{10}^{s}=2108 \mathrm{~cm}^{-1}\),\(g_{a a a}=g_{s s s}=32 \mathrm{~cm}^{-1}\), y\(g_{s s a}=g_{a a s}=22 \mathrm{~cm}^{-1}\). Siempre que se conozca el origen del acoplamiento y su dependencia espacial o angular, se pueden utilizar estos parámetros para obtener una estructura.
Referencias
1. Khalil M, Tokmakoff A. “Firmas de interacciones vibracionales en espectroscopía infrarroja bidimensional coherente”. Chem Phys. 2001; 266 (2-3) :213-30; Khalil M, Demirdöven N, Tokmakoff A. “Espectroscopia IR 2D coherente: Estructura molecular y dinámica en solución”. J Phys Chem A. 2003; 107 (27) :5258-79; Woutersen S, Hamm P. Espectroscopia vibracional bidimensional no lineal de péptidos. J Phys: Condis Mat. 2002; 14:1035-62.

