5.5: Espectroscopia bidimensional para caracterizar la difusión espectral

Un enfoque más intuitivo, aunque difícil, para caracterizar la difusión espectral es con una técnica de correlación bidimensional. Volviendo a nuestro ejemplo de un experimento de doble resonancia, describamos la respuesta de un lineshape no homogéneo con ancho\(\Delta\) y frecuencia media\(\langle\omega_{ab}\rangle\), que se compone de una distribución de transiciones homogéneas de ancho\(\Gamma\). Ahora someteremos el sistema a excitación por un campo de bombeo de banda estrecha, y sondearemos la absorción diferencial\(\Delta A\) en todas las frecuencias de la sonda. Luego repetimos esto para todas las frecuencias de bombeo:

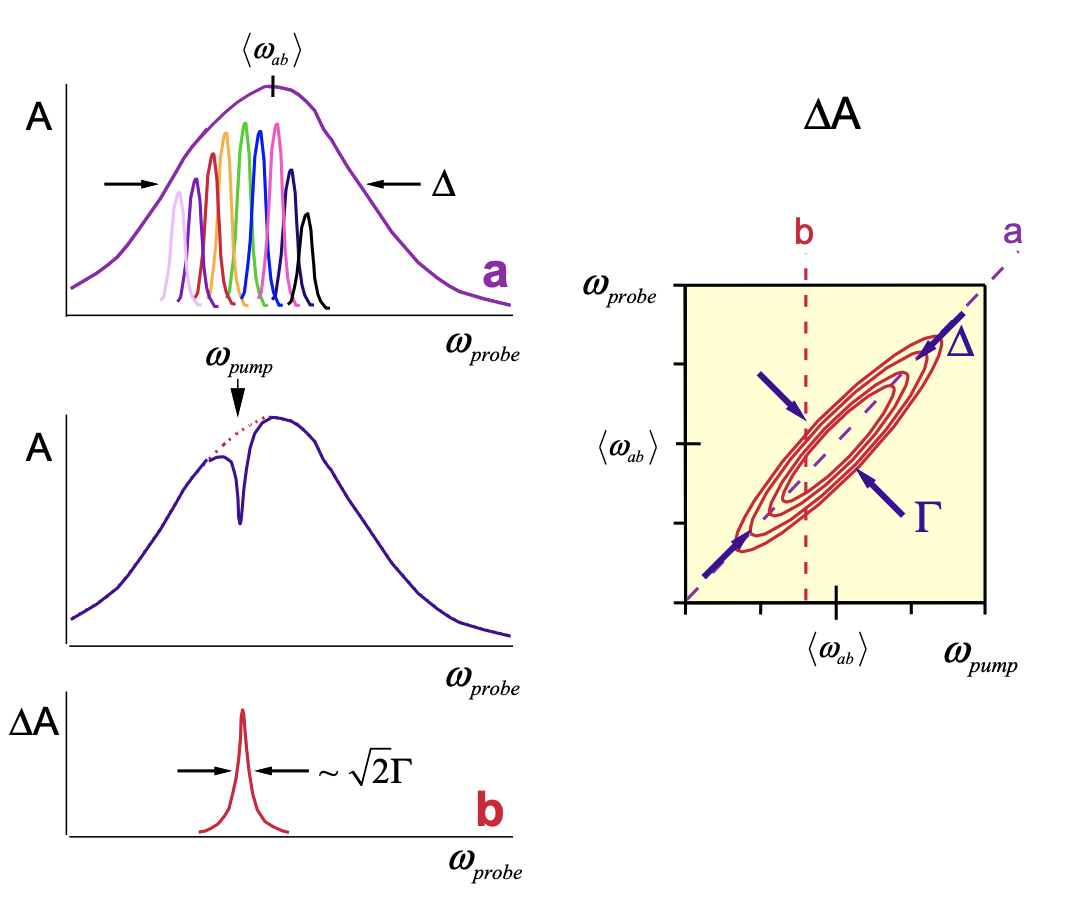
Al construir una representación bidimensional de este espectro de correlación, observamos que la forma de línea observada es alargada a lo largo del eje diagonal\((\omega_1=\omega_3)\). El ancho de línea diagonal está relacionado con el ancho no homogéneo\(\Delta\) mientras que el ancho antidiagonal\(\left[\omega_1+\omega_3=\langle\omega_{ab}\rangle/2\right]\) está determinado por el ancho de línea homogéneo\(\Gamma\).

Para el sistema que exhibe difusión espectral, reconocemos que podemos introducir un tiempo de espera\(\tau_2\) entre la excitación y la detección, lo que proporciona un periodo controlado durante el cual el sistema puede evolucionar. Se puede ver que cuando\(\tau_2\) varía de mucho menos a mucho mayor que el tiempo de correlación,\(\tau_c\), que el lineshape gradualmente se volverá simétrico.

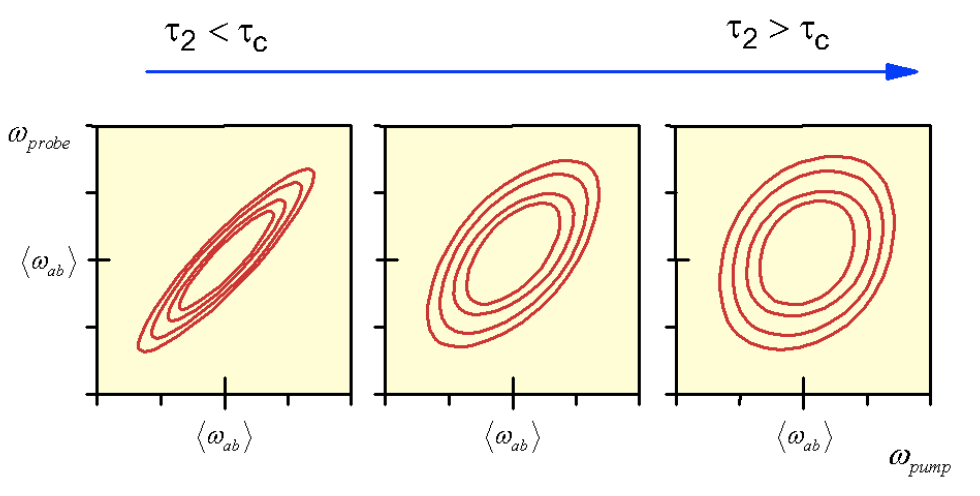
Esto refleja el hecho de que en tiempos prolongados el sistema excitado a cualquier frecuencia se puede observar en cualquier otra con probabilidad de equilibrio. Es decir, la correlación entre las frecuencias de excitación y detección se desvanece.

\[\begin{array}{l} \sum_{i j}\left\langle\delta\left(\omega_{1}-\omega_{e g}^{(i)}\right) \delta\left(\omega_{3}-\omega_{e g}^{(j)}\right)\right\rangle \\ \quad \rightarrow \sum_{i j}\left\langle\delta\left(\omega_{1}-\omega_{e g}^{(i)}\right)\right\rangle\left\langle\delta\left(\omega_{3}-\omega_{e g}^{(j)}\right)\right\rangle \end{array} \label{10.1}\]

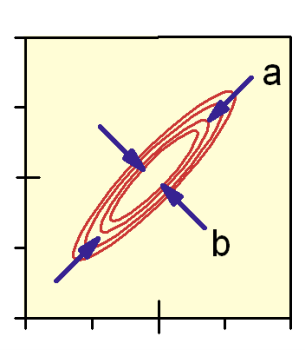Para caracterizar la función de correlación de brecha de energía, elegimos una métrica que describe el cambio como una función de\(\tau_2\). Por ejemplo, la elipticidad

\[E\left(\tau_{2}\right)=\frac{a^{2}-b^{2}}{a^{2}+b^{2}} \label{10.2}\]

es directamente proporcional a\(C_{eg}(\tau)\).

El experimento de eco de fotones es la versión en el dominio del tiempo de este experimento de doble resonancia o quema de agujeros. Si examinamos\(R_2\) en los límites no homogéneos y homogéneos, podemos trazar la envolvente de polarización en función de\(\tau_1\) y\(\tau_3\).

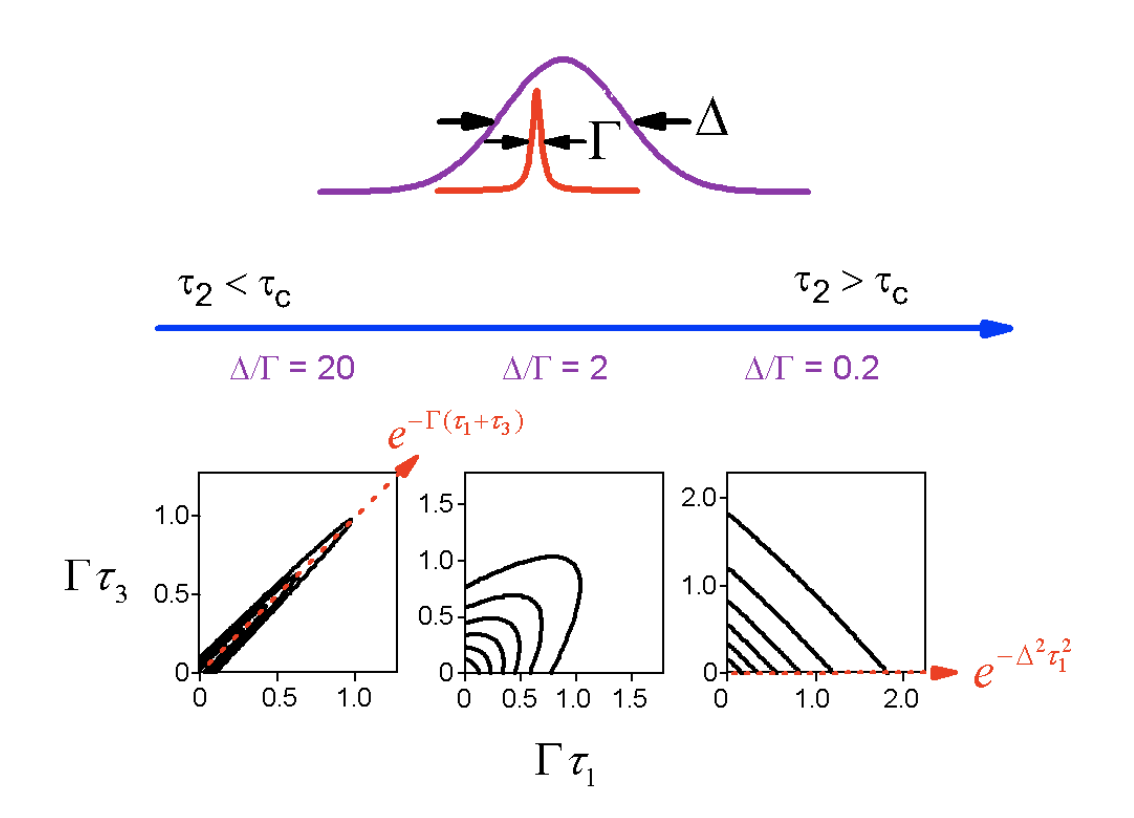
En el límite no homogéneo, una cresta de eco se descompone según\(e^{-\Gamma t}\) se extiende a lo largo\(\tau_1=\tau_3\). Decae con la distribución no homogénea en la dirección perpendicular. En el límite homogéneo, la respuesta es simétrica en las dos variables de tiempo. La transformación de Fourier permite que estas envolventes se expresen como las formas de línea anteriores. Aquí nuevamente\(\tau_2\) se encuentra una variable de control que nos permite caracterizar a\(C_{eg}(\tau)\) través del cambio en el perfil de eco o la forma de línea.