20.1: Estabilidad nuclear y desintegración radiactiva
- Page ID
- 72693
- Escribir y equilibrar ecuaciones nucleares
- Conocer los diferentes tipos de desintegración radiactiva.
- Para equilibrar una reacción nuclear.
La química nuclear es el estudio de reacciones que implican cambios en la estructura nuclear. El capítulo sobre átomos, moléculas e iones introdujo la idea básica de la estructura nuclear, que el núcleo de un átomo está compuesto por protones y, con la excepción de\(\ce{^1_1H}\), neutrones. Recordemos que el número de protones en el núcleo se llama el número atómico (\(Z\)) del elemento, y la suma del número de protones y el número de neutrones es el número de masa (\(A\)). Los átomos con el mismo número atómico pero diferentes números de masa son isótopos del mismo elemento. Cuando nos referimos a un solo tipo de núcleo, a menudo usamos el término nucleido y lo identificamos por la notación:
\[ \large \ce{^{A}_{Z}X} \label{Eq1a} \]
donde
- \(X\)es el símbolo del elemento,
- \(A\)es el número de masa, y
- \(Z\)es el número atómico.
A menudo, un nucleido es referenciado por el nombre del elemento seguido de un guión y el número de masa. Por ejemplo,\(\ce{^{14}_6C}\) se llama “carbono-14".
Los protones y neutrones, llamados colectivamente nucleones, están agrupados firmemente en un núcleo. Con un radio de aproximadamente 10 −15 metros, un núcleo es bastante pequeño en comparación con el radio de todo el átomo, que es de aproximadamente 10 −10 metros. Los núcleos son extremadamente densos en comparación con la materia a granel, promediando\(1.8 \times 10^{14}\) gramos por centímetro cúbico. Por ejemplo, el agua tiene una densidad de 1 gramo por centímetro cúbico, y el iridio, uno de los elementos más densos conocidos, tiene una densidad de 22.6 g/cm 3. Si la densidad de la tierra fuera igual a la densidad nuclear promedio, el radio de la tierra sería de solo unos 200 metros (el radio real de la tierra es aproximadamente\(6.4 \times 10^6\) metros, 30,000 veces mayor).
Los cambios de núcleos que resultan en cambios en sus números atómicos, números de masa o estados energéticos son reacciones nucleares. Para describir una reacción nuclear, utilizamos una ecuación que identifica los nucleidos involucrados en la reacción, sus números másicos y números atómicos, y las otras partículas involucradas en la reacción.
Ecuaciones Nucleares
Una ecuación de reacción química equilibrada refleja el hecho de que durante una reacción química, los enlaces se rompen y se forman, y los átomos se reordenan, pero los números totales de átomos de cada elemento se conservan y no cambian. Una ecuación equilibrada de reacción nuclear indica que hay un reordenamiento durante una reacción nuclear, pero de partículas subatómicas en lugar de átomos. Las reacciones nucleares también siguen las leyes de conservación, y se equilibran de dos maneras:
- La suma de los números de masa de los reactivos es igual a la suma de los números de masa de los productos.
- La suma de las cargas de los reactivos equivale a la suma de las cargas de los productos.
Si se conoce el número atómico y el número másico de todas las partículas menos una de las partículas en una reacción nuclear, podemos identificar la partícula equilibrando la reacción. Por ejemplo, podríamos determinar que\(\ce{^{17}_8O}\) es producto de la reacción nuclear de\(\ce{^{14}_7N}\) y\(\ce{^4_2He}\) si supiéramos que un protón,\(\ce{^1_1H}\), era uno de los dos productos. \(\PageIndex{1}\)El ejemplo muestra cómo podemos identificar un nucleido equilibrando la reacción nuclear.
La reacción de una partícula α con magnesio-25\( (\ce{^{25}_{12}Mg})\) produce un protón y un nucleido de otro elemento. Identificar el nuevo nucleido producido.
Solución
La reacción nuclear puede escribirse como:
\[\ce{^{25}_{12}Mg + ^4_2He \rightarrow ^1_1H + ^{A}_{Z}X} \nonumber \]
donde
- \(\ce A\)es el número de masa y
- \(\ce Z\)es el número atómico del nuevo nucleido,\(\ce X\).
Porque la suma de los números de masa de los reactivos debe ser igual a la suma de los números de masa de los productos:
\[\mathrm{25+4=A+1} \nonumber \]
por lo
\[ \mathrm{A=28} \nonumber \]
De igual manera, los cargos deben equilibrar, por lo que:
\[\mathrm{12+2=Z+1} \nonumber \]
por lo
\[\mathrm{Z=13} \nonumber \]
Consultar la tabla periódica: El elemento con carga nuclear = +13 es aluminio. Así, el producto es\(\ce{^{28}_{13}Al}\).
El nucleido se\(\ce{^{125}_{53}I}\) combina con un electrón y produce un nuevo núcleo y ninguna otra partícula masiva. ¿Cuál es la ecuación para esta reacción?
- Responder
-
\[\ce{^{125}_{53}I + ^0_{−1}e \rightarrow ^{125}_{52}Te} \nonumber \]
Los dos tipos generales de reacciones nucleares son las reacciones de desintegración nuclear y las reacciones de transmutación nuclear. En una reacción de desintegración nuclear, también llamada desintegración radiactiva, un núcleo inestable emite radiación y se transforma en el núcleo de uno o más de otros elementos. Los núcleos hijos resultantes tienen una masa menor y son más bajos en energía (más estables) que el núcleo parental que se desintegró. En contraste, en una reacción de transmutación nuclear, un núcleo reacciona con una partícula subatómica u otro núcleo para formar un núcleo producto que es más masivo que el material de partida. Como veremos, las reacciones de desintegración nuclear ocurren espontáneamente bajo todas las condiciones, pero las reacciones de transmutación nuclear ocurren sólo bajo condiciones muy especiales, como la colisión de un haz de partículas altamente energéticas con un núcleo objetivo o en el interior de las estrellas. Comenzamos esta sección considerando las diferentes clases de núcleos radiactivos, junto con sus características reacciones de desintegración nuclear y la radiación que emiten.
Las reacciones de desintegración nuclear ocurren espontáneamente en todas las condiciones, mientras que las reacciones de transmutación nuclear son inducidas.
Reacciones de desintegración nuclear
Así como usamos el número y tipo de átomos presentes para equilibrar una ecuación química, podemos usar el número y tipo de nucleones presentes para escribir una ecuación nuclear equilibrada para una reacción de desintegración nuclear. Este procedimiento también nos permite predecir la identidad del núcleo padre o hijo si se conoce la identidad de uno solo. Independientemente del modo de desintegración, el número total de nucleones se conserva en todas las reacciones nucleares.
Para describir las reacciones de desintegración nuclear, los químicos han extendido la\(^A _Z \textrm{X}\) notación de nucleidos para incluir emisiones radiactivas. En la tabla se\(\PageIndex{1}\) enumera el nombre y el símbolo de cada tipo de radiación emitida. La adición más notable es el positrón, una partícula que tiene la misma masa que un electrón pero una carga positiva más que una carga negativa.
| Identidad | Símbolo | Cargar | Masa (amu) |
|---|---|---|---|
| núcleo de helio | \(^4_2\alpha\) | +2 | 4.001506 |
| electrón | \(^0_{-1}\beta\)o\(\beta ^-\) | −1 | 0.000549 |
| fotón | \(_0^0\gamma\) | — | — |
| neutrones | \(^1_0\textrm n\) | 0 | 1.008665 |
| protón | \(^1_1\textrm p \) | +1 | 1.007276 |
| positrón | \(^0_{+1}\beta\)o\(\beta ^+\) | +1 | 0.000549 |
Al igual que la notación utilizada para indicar isótopos, el superíndice superior izquierdo en el símbolo para una partícula da el número de masa, que es el número total de protones y neutrones. Para un protón o un neutrón, A = 1. Debido a que ni un electrón ni un positrón contienen protones o neutrones, su número de masa es 0. Los números no deben tomarse literalmente, sin embargo, en el sentido de que estas partículas tienen masa cero; la expulsión de una partícula beta (un electrón) simplemente tiene un efecto insignificante sobre la masa de un núcleo.
De igual manera, el subíndice inferior izquierdo da la carga de la partícula. Debido a que los protones llevan una carga positiva, Z = +1 para un protón. En contraste, un neutrón no contiene protones y es eléctricamente neutro, por lo que Z = 0. En el caso de un electrón, Z = −1, y para un positrón, Z = +1. Debido a que los rayos γ son fotones de alta energía, tanto A como Z son 0. En algunos casos, se utilizan dos símbolos diferentes para partículas que son idénticas pero producidas de diferentes maneras. Por ejemplo, el símbolo\(^0_{-1}\textrm e\), que suele simplificarse a e −, representa un electrón libre o un electrón asociado a un átomo, mientras que el símbolo\(^0_{-1}\beta\), que a menudo se simplifica a β −, denota un electrón que se origina desde dentro del núcleo, que es un β partícula. De igual manera,\(^4_{2}\textrm{He}^{2+}\) se refiere al núcleo de un átomo de helio, y\(^4_{2}\alpha\) denota una partícula idéntica que ha sido expulsada de un núcleo más pesado.
Hay seis tipos fundamentalmente diferentes de reacciones de desintegración nuclear, y cada una libera un tipo diferente de partícula o energía. Las características esenciales de cada reacción se muestran en la Figura\(\PageIndex{1}\). Los más comunes son la desintegración alfa y beta y la emisión gamma, pero los otros son esenciales para comprender las reacciones de desintegración nuclear.
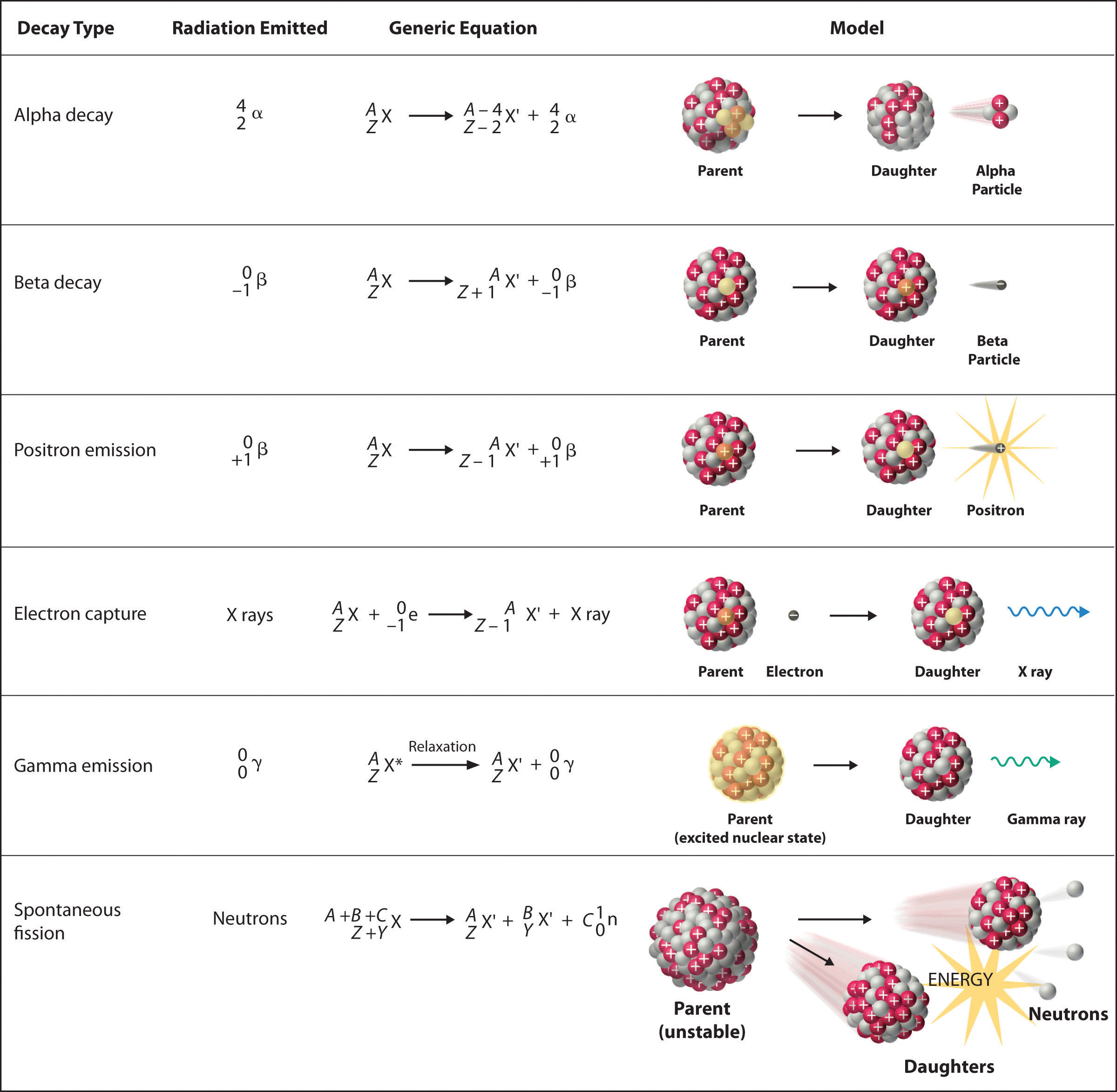
\(\alpha\)Decaimiento Alfa
Muchos núcleos con números de masa mayores a 200 sufren desintegración alfa (α), lo que resulta en la emisión de un núcleo de helio-4 como una partícula alfa (α),\(^4_{2}\alpha\). La reacción general es la siguiente:
\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A-4}_{Z-2} \textrm X'}+\underset{\textrm{alpha}\\ \textrm{particle}}{^4_2 \alpha}\label{Eq1} \]
El nucleido hijo contiene dos protones menos y dos neutrones menos que el padre. Así, la emisión de partículas αproduce un núcleo hijo con un número de masa A − 4 y una carga nuclear Z − 2 en comparación con el núcleo parental. El radio-226, por ejemplo, sufre desintegración alfa para formar radón-222:
\[^{226}_{88}\textrm{Ra}\rightarrow ^{222}_{86}\textrm{Rn}+^{4}_{2}\alpha\label{Eq2} \]
Debido a que los nucleones se conservan en esta y todas las demás reacciones nucleares, la suma de los números de masa de los productos, 222 + 4 = 226, equivale al número de masa del progenitor. De igual manera, la suma de los números atómicos de los productos, 86 + 2 = 88, equivale al número atómico del padre. Así se equilibra la ecuación nuclear.
Así como el número total de átomos se conserva en una reacción química, el número total de nucleones se conserva en una reacción nuclear.
\(\beta^-\)Decaimiento Beta
Los núcleos que contienen demasiados neutrones suelen sufrir desintegración beta (β), en la que un neutrón se convierte en protón y un electrón de alta energía que se expulsa del núcleo como una partícula β:
\[\underset{\textrm{unstable} \\ \textrm{neutron in} \\ \textrm{nucleus}}{^1_0 \textrm n}\rightarrow \underset{\textrm{proton} \\ \textrm{retained} \\ \textrm{by nucleus}}{^{1}_{1} \textrm p}+\underset{\textrm{beta particle} \\ \textrm{emitted by} \\ \textrm{nucleus}}{^0_{-1} \beta}\label{Eq3} \]
Por lo tanto, la reacción general para la desintegración beta es
\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z+1} \textrm X'}+\underset{\textrm{beta particle}}{^0_{-1} \beta}\label{Eq4} \]
Aunque la desintegración beta no cambia el número de masa del núcleo, sí resulta en un incremento de +1 en el número atómico debido a la adición de un protón en el núcleo hijo. Así, la desintegración beta disminuye la relación neutrón-protón, moviendo el núcleo hacia la banda de núcleos estables. Por ejemplo, el carbono-14 experimenta desintegración beta para formar nitrógeno-14:
\[^{14}_{6}\textrm{C}\rightarrow ^{14}_{7}\textrm{N}+\,^{0}_{-1}\beta \nonumber \]
Una vez más, se conserva el número de nucleones y se equilibran las cargas. Los núcleos padre e hijo tienen el mismo número de masa, 14, y la suma de los números atómicos de los productos es 6, que es el mismo que el número atómico del progenitor carbono-14.
\(\beta^+\)Emisión de positrones
Debido a que un positrón tiene la misma masa que un electrón pero carga opuesta, la emisión de positrones es lo opuesto a la desintegración beta. Así, la emisión de positrones es característica de núcleos pobres en neutrones, que se descomponen transformando un protón en un neutrón y emitiendo un positrón de alta energía:
\[^{1}_{1}\textrm{p}^+\rightarrow ^{1}_{0}\textrm{n}+\,^{0}_{+1}\beta^+\label{Eq6} \]
La reacción general para la emisión de positrones es por lo tanto
\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z-1} \textrm X'}+\underset{\textrm{positron}}{^0_{+1} \beta^+} \nonumber \]
Al igual que la desintegración beta, la emisión de positrones no cambia el número de masa del núcleo. En este caso, sin embargo, el número atómico del núcleo hijo es menor en 1 que el del progenitor. Así, la relación neutrón-protón ha aumentado, moviendo nuevamente el núcleo más cerca de la banda de núcleos estables. Por ejemplo, el carbono-11 experimenta emisión de positrones para formar boro-11:
\[^{11}_{6}\textrm{C}\rightarrow ^{11}_{5}\textrm{B}+\,^{0}_{+1}\beta^+ \nonumber \]
Los nucleones se conservan y las cargas se equilibran. El número de masa, 11, no cambia, y la suma de los números atómicos de los productos es 6, lo mismo que el número atómico del nucleido carbono-11 padre.
Captura de electrones
Un núcleo pobre en neutrones puede descomponerse por emisión de positrones o captura de electrones (EC), en la que un electrón en una capa interna reacciona con un protón para producir un neutrón:
\[^{1}_{1}\textrm{p} +\; ^{0}_{-1}\textrm{e}\rightarrow \, ^{1}_{0}\textrm n\label{Eq9} \]
Cuando un segundo electrón se mueve desde una capa externa para tomar el lugar del electrón de menor energía que fue absorbido por el núcleo, se emite una radiografía. Por lo tanto, la reacción general para la captura de electrones es
\[\underset{\textrm{parent}}{^A_Z \textrm X}+\underset{\textrm{electron}}{^0_{-1} \textrm e}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z-1} \textrm X'}+\textrm{x-ray} \nonumber \]
La captura de electrones no cambia el número de masa del núcleo porque tanto el protón que se pierde como el neutrón que se forma tienen un número de masa de 1. Al igual que con la emisión de positrones, sin embargo, el número atómico del núcleo hijo es menor en 1 que el del progenitor. Una vez más, la relación neutrón-protón ha aumentado, moviendo el núcleo hacia la banda de núcleos estables. Por ejemplo, el hierro-55 se descompone por captura de electrones para formar manganeso-55, que a menudo se escribe de la siguiente manera:
\[^{55}_{26}\textrm{Fe}\overset{\textrm{EC}}{\rightarrow}\, ^{55}_{25}\textrm{Mn}+\textrm{x-ray} \nonumber \]
Los números atómicos de los nucleidos padre e hijo difieren en la Ecuación 20.2.11, aunque los números de masa son los mismos. Para escribir una ecuación nuclear equilibrada para esta reacción, debemos incluir explícitamente el electrón capturado en la ecuación:
\[^{55}_{26}\textrm{Fe}+\,^{0}_{-1}\textrm{e}\rightarrow \, ^{55}_{25}\textrm{Mn}+\textrm{x-ray} \nonumber \]
Tanto la emisión de positrones como la captura de electrones generalmente se observan para nucleidos con bajas relaciones neutrón-protón, pero las tasas de desintegración para los dos procesos pueden ser muy diferentes.
\(\gamma\)Emisión Gamma
Muchas reacciones de desintegración nuclear producen núcleos hijos que se encuentran en un estado excitado nuclear, que es similar a un átomo en el que un electrón ha sido excitado a un orbital de mayor energía para dar un estado excitado electrónico. Así como un electrón en estado excitado electrónico emite energía en forma de fotón cuando vuelve al estado fundamental, un núcleo en estado excitado libera energía en forma de fotón cuando vuelve al estado fundamental. Estos fotones de alta energía son rayos γ. La emisión gamma (\(\gamma\)) puede ocurrir virtualmente instantáneamente, como ocurre en la desintegración alfa del uranio-238 a torio-234, donde el asterisco denota un estado excitado:
\[^{238}_{92}\textrm{U}\rightarrow \, \underset{\textrm{excited} \\ \textrm{nuclear} \\ \textrm{state}}{^{234}_{90}\textrm{Th*}} + ^{4}_{2}\alpha\xrightarrow {\textrm{relaxation}\,}\,^{234}_{90}\textrm{Th} + \ce{^0_0\gamma} \nonumber \]
Si ignoramos el evento de decaimiento que creó el núcleo excitado, entonces
\[^{234}_{88}\textrm{Th*} \rightarrow\, ^{234}_{88}\textrm{Th} + ^{0}_{0}\gamma \nonumber \]
o más generalmente,
\[^{A}_{Z}\textrm{X*} \rightarrow\, ^{A}_{Z}\textrm{X} + ^{0}_{0}\gamma \nonumber \]
La emisión gamma también puede ocurrir después de un retraso significativo. Por ejemplo, el tecnecio-99 m tiene una vida media de aproximadamente 6 horas antes de emitir un\(γ\) rayo para formar tecnecio-99 (la m es para metaestable). Debido a que los rayos γ son energía, su emisión no afecta ni al número másico ni al número atómico del nucleido hijo. Por lo tanto, la emisión de rayos gamma es el único tipo de radiación que no necesariamente implica la conversión de un elemento a otro, aunque casi siempre se observa junto con alguna otra reacción de desintegración nuclear.
Fsión espontánea
Sólo núcleos muy masivos con altas proporciones neutrón-protón pueden sufrir fisión espontánea, en la que el núcleo se rompe en dos piezas que tienen diferentes números atómicos y masas atómicas. Este proceso es más importante para los elementos transactinidas, con Z ≥ 104. La fisión espontánea va acompañada invariablemente de la liberación de grandes cantidades de energía, y suele ir acompañada también de la emisión de varios neutrones. Un ejemplo es la fisión espontánea de\(^{254}_{98}\textrm{Cf}\), que da una distribución de los productos de fisión; un posible conjunto de productos se muestra en la siguiente ecuación:
\[^{254}_{98}\textrm{Cf}\rightarrow \,^{118}_{46}\textrm{Pd}+\,^{132}_{52}\textrm{Te}+4^{1}_{0}\textrm{n} \nonumber \]
Una vez más, se conserva el número de nucleones. Así, la suma de los números de masa de los productos (118 + 132 + 4 = 254) es igual al número de masa del reactivo. De igual manera, la suma de los números atómicos de los productos [46 + 52 + (4 × 0) = 98] es la misma que el número atómico del nucleido padre.
Escribir una ecuación nuclear equilibrada para describir cada reacción.
- la desintegración beta de\(^{35}_{16}\textrm{S}\)
- la decadencia de\(^{201}_{80}\textrm{Hg}\) por captura de electrones
- la descomposición de\(^{30}_{15}\textrm{P}\) por emisión de positrones
Dado: nucleido radiactivo y modo de desintegración
Preguntado por: ecuación nuclear balanceada
Estrategia:
A Identificar los reactivos y los productos a partir de la información proporcionada.
B Utilice los valores de A y Z para identificar los componentes faltantes necesarios para equilibrar la ecuación.
Solución
a.
A Conocemos las identidades del reactivo y uno de los productos (una partícula β). Por lo tanto, podemos comenzar escribiendo una ecuación que muestre el reactivo y uno de los productos e indique el producto desconocido como\(^{A}_{Z}\textrm{X}\):\[^{35}_{16}\textrm{S}\rightarrow\,^{A}_{Z}\textrm{X}+\,^{0}_{-1}\beta \nonumber \]
B Debido a que tanto los protones como los neutrones deben conservarse en una reacción nuclear, el producto desconocido debe tener un número de masa de A = 35 − 0 = 35 y un número atómico de Z = 16 − (−1) = 17. El elemento con Z = 17 es cloro, por lo que la ecuación nuclear balanceada es la siguiente:\[^{35}_{16}\textrm{S}\rightarrow\,^{35}_{17}\textrm{Cl}+\,^{0}_{-1}\beta \nonumber \]
b.A Conocemos las identidades de ambos reactivos:\(^{201}_{80}\textrm{Hg}\) y un electrón interno,\(^{0}_{-1}\textrm{e}\). La reacción es la siguiente:\[^{201}_{80}\textrm{Hg}+\,^{0}_{-1}\textrm e\rightarrow\,^{A}_{Z}\textrm{X} \nonumber \]
B Se conservan tanto protones como neutrones, por lo que el número de masa del producto debe ser A = 201 + 0 = 201, y el número atómico del producto debe ser Z = 80 + (−1) = 79, que corresponde al elemento oro. La ecuación nuclear equilibrada es, por lo tanto\[^{201}_{80}\textrm{Hg}+\,^{0}_{-1}\textrm e\rightarrow\,^{201}_{79}\textrm{Au} \nonumber \]
c.A Como en la parte (a), se nos dan las identidades del reactivo y uno de los productos, en este caso, un positrón. Por lo tanto, la ecuación nuclear desequilibrada es\[^{30}_{15}\textrm{P}\rightarrow\,^{A}_{Z}\textrm{X}+\,^{0}_{+1}\beta \nonumber \]
B El número de masa del segundo producto es A = 30 − 0 = 30, y su número atómico es Z = 15 − 1 = 14, que corresponde al silicio. La ecuación nuclear equilibrada para la reacción es la siguiente:\[^{30}_{15}\textrm{P}\rightarrow\,^{30}_{14}\textrm{Si}+\,^{0}_{+1}\beta \nonumber \]
Escribir una ecuación nuclear equilibrada para describir cada reacción.
- \(^{11}_{6}\textrm{C}\)por emisión de positrones
- la desintegración beta del molibdeno-99
- la emisión de una partícula α seguida de la emisión gamma de\(^{185}_{74}\textrm{W}\)
- Responder a
-
\(^{11}_{6}\textrm{C}\rightarrow\,^{11}_{5}\textrm{B}+\,^{0}_{+1}\beta\)
- Respuesta d
-
\(^{99}_{42}\textrm{Mo}\rightarrow\,^{99m}_{43}\textrm{Tc}+\,^{0}_{-1}\beta\)
- Respuesta c
-
\(^{185}_{74}\textrm{W}\rightarrow\,^{181}_{72}\textrm{Hf}+\,^{4}_{2}\alpha +\,^{0}_{0}\gamma\)
Predecir el tipo de cambio nuclear que experimenta cada nucleido inestable cuando decae.
- \(^{45}_{22}\textrm{Ti}\)
- \(^{242}_{94}\textrm{Pu}\)
- \(^{12}_{5}\textrm{B}\)
- \(^{256}_{100}\textrm{Fm}\)
Dado: nucleido
Preguntado por: tipo de desintegración nuclear
Estrategia:
Con base en la relación neutrón-protón y el valor de Z, predecir el tipo de reacción de desintegración nuclear que producirá un nucleido más estable.
Solución
- Este nucleido tiene una relación neutrón-protón de sólo 1.05, que es mucho menor que el requisito de estabilidad para un elemento con un número atómico en este rango. Los núcleos que tienen bajas relaciones neutrón-protón se descomponen al convertir un protón en un neutrón. Las dos posibilidades son la emisión de positrones, que convierte un protón en un neutrón y un positrón, y la captura de electrones, que convierte un protón y un electrón central en un neutrón. En este caso, se observan ambos, con emisión de positrones ocurriendo alrededor del 86% del tiempo y captura de electrones alrededor del 14% del tiempo.
- Los núcleos con Z > 83 son demasiado pesados para ser estables y suelen sufrir desintegración alfa, lo que disminuye tanto el número másico como el número atómico. Por lo tanto,\(^{242}_{94}\textrm{Pu}\) se espera que la desintegración por emisión alfa.
- Este nucleido tiene una relación neutrón-protón de 1.4, que es muy alta para un elemento ligero. Los núcleos con altas relaciones neutrón-protón se descomponen al convertir un neutrón en un protón y un electrón. El electrón se emite como una partícula β, y el protón permanece en el núcleo, provocando un aumento en el número atómico sin cambio en el número de masa. Por lo tanto, predecimos que\(^{12}_{5}\textrm{B}\) sufrirá desintegración beta.
- Se trata de un nucleido masivo, con un número atómico de 100 y un número de masa mucho mayor que 200. Los nucleidos con A ≥ 200 tienden a descomponerse por emisión alfa, e incluso los núcleos más pesados tienden a sufrir fisión espontánea. Por lo tanto, predecimos que\(^{256}_{100}\textrm{Fm}\) se desintegrará por uno o ambos de estos dos procesos. De hecho, decae tanto por fisión espontánea como por emisión alfa, en una proporción 97:3.
Predecir el tipo de cambio nuclear que experimenta cada nucleido inestable cuando decae.
- \(^{32}_{14}\textrm{Si}\)
- \(^{43}_{21}\textrm{Sc}\)
- \(^{231}_{91}\textrm{Pa}\)
- Responder a
-
decaimiento beta
- Respuesta d
-
emisión de positrones o captura de electrones
- Respuesta c
-
desintegración alfa
Serie de desintegración radiactiva
Los núcleos de todos los elementos con números atómicos mayores a 83 son inestables. Así, todos los isótopos de todos los elementos más allá del bismuto en la tabla periódica son radiactivos. Debido a que la desintegración alfa disminuye Z en solo 2, y la emisión de positrones o la captura de electrones disminuye Z en solo 1, es imposible que cualquier nucleido con Z > 85 se descomponga a un nucleido hijo estable en un solo paso, excepto por fisión nuclear. En consecuencia, los isótopos radiactivos con Z > 85 generalmente se descomponen en un núcleo hijo que es radiactivo, que a su vez se descompone en un segundo núcleo hijo radiactivo, y así sucesivamente, hasta que finalmente resulta un núcleo estable. Esta serie de alfa secuencial- y reacciones de desintegración beta se llama serie de desintegración radiactiva. La más común es la serie de desintegración de uranio-238, que produce plomo-206 en una serie de 14 reacciones secuenciales de desintegración alfa y beta (Figura\(\PageIndex{2}\)). Si bien se puede escribir una serie de desintegración radiactiva para casi cualquier isótopo con Z > 85, solo otras dos ocurren de forma natural: la desintegración del uranio-235 a plomo-207 (en 11 pasos) y torio-232 a plomo-208 (en 10 pasos). Se sabe que una cuarta serie, la desintegración del neptunio-237 a bismuto-209 en 11 pasos, ocurrió en la Tierra primitiva. Con una vida media de “solo” 2.14 millones de años, todo el neptunio-237 presente cuando se formó la Tierra decayó hace mucho tiempo, y hoy todo el neptunio en la Tierra es sintético.
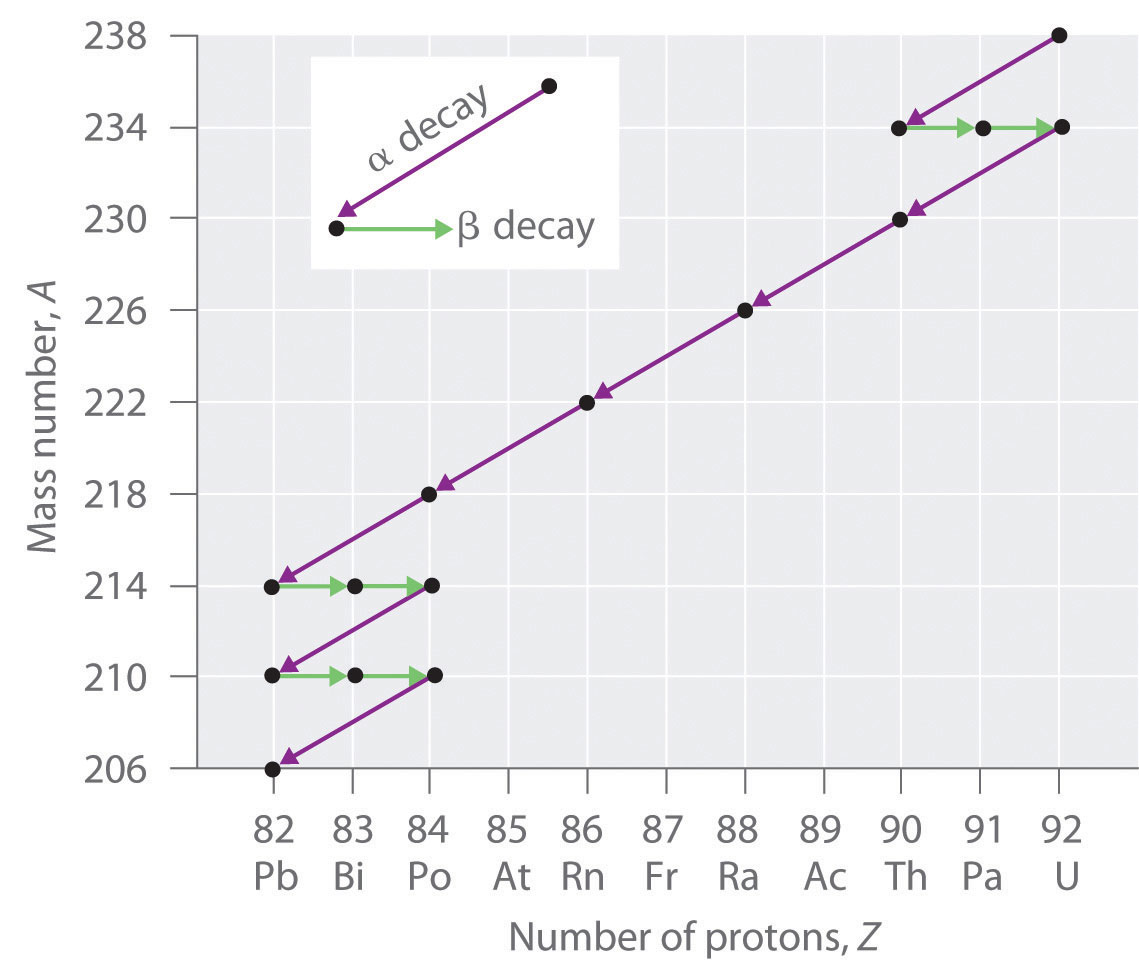
Debido a estas series de desintegración radiactiva, pequeñas cantidades de isótopos muy inestables se encuentran en minerales que contienen uranio o torio. Estos isótopos raros e inestables deberían haberse decaído hace mucho tiempo a núcleos estables con un número atómico menor, y ya no se encontrarían en la Tierra. Debido a que son generados continuamente por la desintegración del uranio o torio, sin embargo, sus cantidades han alcanzado un estado estacionario, en el que su tasa de formación es igual a su tasa de descomposición. En algunos casos, la abundancia de los isótopos hijos se puede utilizar para fechar un material o identificar su origen.
Reacciones nucleares inducidas
El descubrimiento de la radiactividad a finales del siglo XIX demostró que algunos núcleos se transforman espontáneamente en núcleos con un número diferente de protones, produciendo así un elemento diferente. Cuando los científicos se dieron cuenta de que estos isótopos radiactivos naturales se descomponían al emitir partículas subatómicas, se dieron cuenta de que, en principio, debería ser posible llevar a cabo la reacción inversa, convirtiendo un núcleo estable en otro núcleo más masivo bombardeándolo con partículas subatómicas en un reacción de transmutación nuclear.
La primera reacción exitosa de transmutación nuclear fue realizada en 1919 por Ernest Rutherford, quien demostró que las partículas α emitidas por el radio podían reaccionar con núcleos de nitrógeno para formar núcleos de oxígeno. Como se muestra en la siguiente ecuación, se emite un protón en el proceso:
\(^{4}_{2}\alpha + \, ^{14}_{7}\textrm{N} \rightarrow \,^{17}_{8}\textrm{O}+\,^{1}_{1}\textrm{p}\label{Eq17}\)
Los experimentos de transmutación nuclear de Rutherford llevaron al descubrimiento del neutrón. Encontró que bombardear el núcleo de un elemento blanco ligero con una partícula α generalmente convirtió el núcleo objetivo en un producto que tenía un número atómico mayor en 1 y un número de masa mayor en 3 que el núcleo objetivo. Dicho comportamiento es consistente con la emisión de un protón después de la reacción con la partícula α. Objetivos muy ligeros como Li, Be y B reaccionaron de manera diferente, sin embargo, emitiendo un nuevo tipo de radiación altamente penetrante en lugar de un protón. Debido a que ni un campo magnético ni un campo eléctrico podían desviar estas partículas de alta energía, Rutherford concluyó que eran eléctricamente neutras. Otras observaciones sugirieron que la masa de la partícula neutra era similar a la masa del protón. En 1932, James Chadwick (Premio Nobel de Física, 1935), quien en ese momento era estudiante de Rutherford, nombró neutrones a estas partículas neutras y propuso que eran bloques de construcción fundamentales del átomo. La reacción que Chadwick utilizó inicialmente para explicar la producción de neutrones fue la siguiente:
\[^{4}_{2}\alpha + \, ^{9}_{4}\textrm{Be} \rightarrow \,^{12}_{6}\textrm{C}+\,^{1}_{0}\textrm{n}\label{Eq18} \]
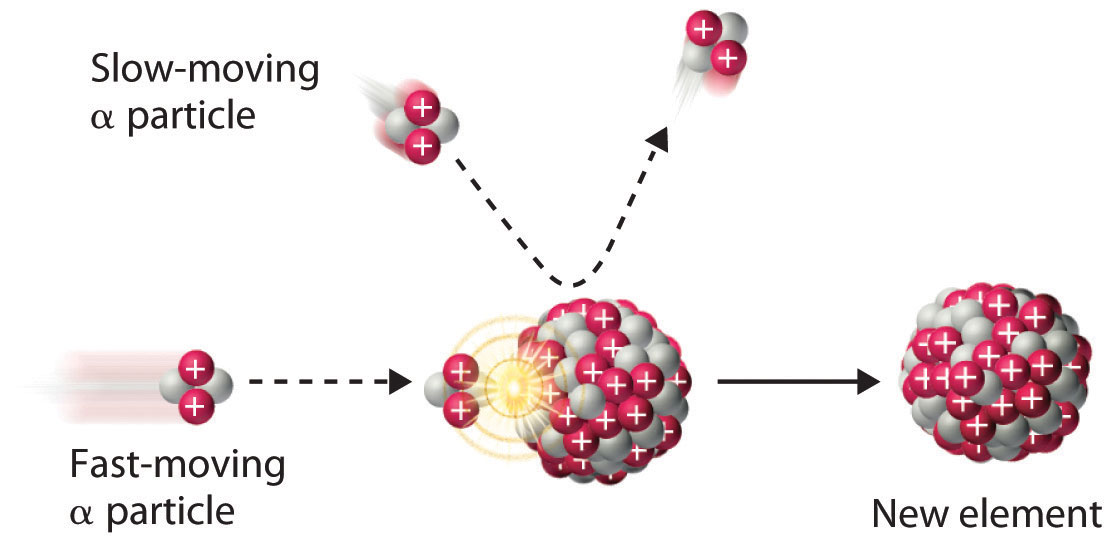
Debido a que las partículas α y los núcleos atómicos están cargados positivamente, las fuerzas electrostáticas hacen que se repelan entre sí. Solo las partículas α con energía cinética muy alta pueden superar esta repulsión y colisionar con un núcleo (Figura\(\PageIndex{3}\)). Los neutrones no tienen carga eléctrica, sin embargo, por lo que no son repelidos por el núcleo. De ahí que el bombardeo con neutrones sea una forma mucho más fácil de preparar nuevos isótopos de los elementos más ligeros. De hecho, el carbono-14 se forma naturalmente en la atmósfera al bombardear el nitrógeno-14 con neutrones generados por los rayos cósmicos:
\[^{1}_{0}\textrm{n} + \, ^{14}_{7}\textrm{N} \rightarrow \,^{14}_{6}\textrm{C}+\,^{1}_{1}\textrm{p}\label{Eq19} \]
En 1933, Frédéric Joliot e Iréne Joliot-Curie (hija de Marie y Pierre Curie) prepararon el primer isótopo radiactivo artificial bombardeando aluminio-27 con partículas α. Por cada 27 Al que reaccionaron, se liberó un neutrón. Identificar el nucleido producto y escribir una ecuación nuclear balanceada para esta reacción de transmutación.
Dado: reactivos en una reacción de transmutación nuclear
Preguntado por: nucleido de producto y ecuación nuclear balanceada
Estrategia:
A Con base en los reactivos y un producto, identificar el otro producto de la reacción. Utilizar la conservación de masa y carga para determinar los valores de Z y A del nucleido producto y así su identidad.
B Escribe la ecuación nuclear balanceada para la reacción.
Solución
A Bombardear un elemento con partículas α generalmente produce un elemento con un número atómico que es 2 mayor que el número atómico del núcleo objetivo. Así se espera que el aluminio (Z = 13) se convierta en fósforo (Z = 15). Con un neutrón liberado, la conservación de la masa requiere que el número de masa del otro producto sea 3 mayor que el número de masa del objetivo. En este caso, el número de masa del objetivo es 27, por lo que el número de masa del producto será 30. El segundo producto es, por lo tanto, fósforo-30,\(^{30}_{15}\textrm{P}\).
B La ecuación nuclear equilibrada para la reacción es la siguiente:
\[^{27}_{13}\textrm{Al} + \, ^{4}_{2}\alpha \rightarrow \,^{30}_{15}\textrm{P}+\,^{1}_{0}\textrm{n} \nonumber \]
Debido a que todos los isótopos del tecnecio son radiactivos y tienen semividas cortas, no existe en la naturaleza. Sin embargo, el tecnecio puede prepararse mediante reacciones de transmutación nuclear. Por ejemplo, bombardear un objetivo molibdeno-96 con núcleos de deuterio\((^{2}_{1}\textrm{H})\) produce tecnecio-97. Identificar el otro producto de la reacción y escribir una ecuación nuclear equilibrada para esta reacción de transmutación.
- Responder
-
neutrones,\(^{1}_{0}\textrm{n}\);\(^{96}_{42}\textrm{Mo} + \, ^{2}_{1}\textrm{H} \rightarrow \,^{97}_{43}\textrm{Tc}+\,^{1}_{0}\textrm{n}\):
Señalamos anteriormente en esta sección que los nucleidos muy pesados, correspondientes a Z ≥ 104, tienden a descomponerse por fisión espontánea. Los nucleidos con valores ligeramente menores de Z, como los isótopos de uranio (Z = 92) y plutonio (Z = 94), no experimentan fisión espontánea a ninguna tasa significativa. Algunos isótopos de estos elementos, sin embargo, como\(^{235}_{92}\textrm{U}\) y\(^{239}_{94}\textrm{Pu}\) experimentan fisión nuclear inducida cuando son bombardeados con neutrones de energía relativamente baja, como se muestra en la siguiente ecuación para uranio-235 y en la Figura\(\PageIndex{4}\):
\[^{235}_{92}\textrm{U} + \, ^{1}_{0}\textrm{n} \rightarrow \,^{236}_{92}\textrm{U}\rightarrow \,^{141}_{56}\textrm{Ba}+\,^{92}_{36}\textrm{Kr}+3^{1}_{0}\textrm{n}\label{Eq20} \]
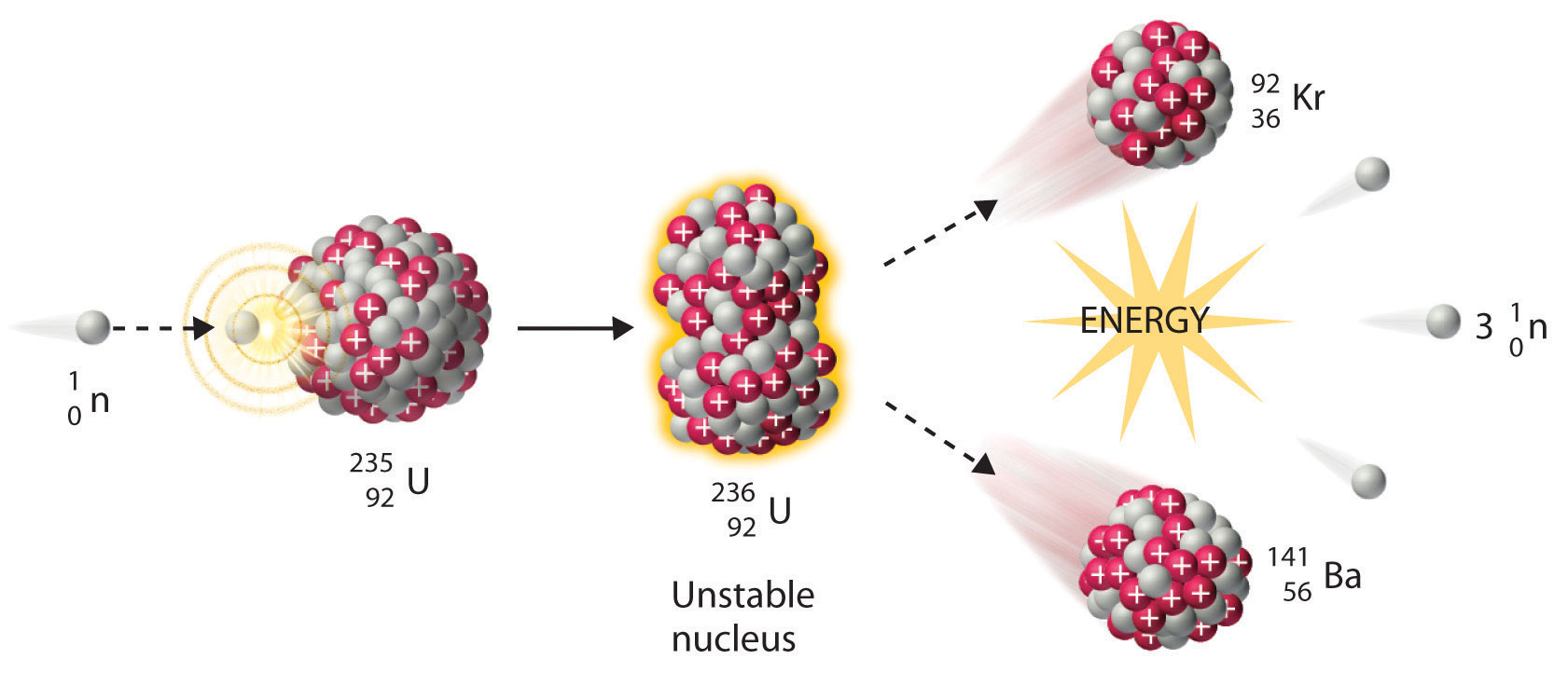
Cualquier isótopo que pueda sufrir una reacción de fisión nuclear cuando se bombardea con neutrones se denomina isótopo fisionable.
Durante la fisión nuclear, el núcleo suele dividirse asimétricamente en lugar de en dos partes iguales, como se muestra en la Figura\(\PageIndex{4}\). Además, cada evento de fisión de un nucleido dado no da los mismos productos; se han identificado más de 50 modos de fisión diferentes para el uranio-235, por ejemplo. En consecuencia, la fisión nuclear de un nucleido fisionable nunca puede ser descrita por una sola ecuación. En cambio, como se muestra en la Figura\(\PageIndex{5}\), se obtiene una distribución de muchos pares de productos de fisión con diferentes rendimientos, pero la relación de masa de cada par de productos de fisión producidos por un solo evento de fisión es siempre aproximadamente 3:2.
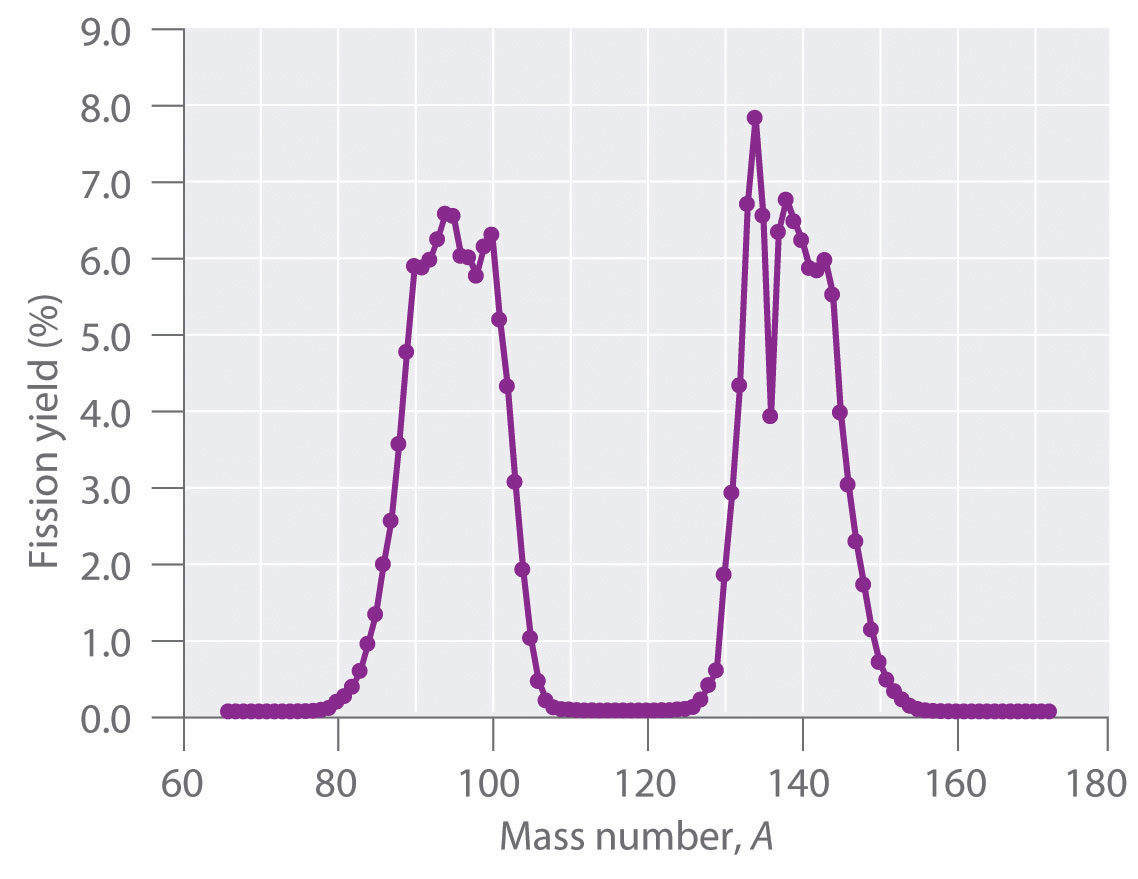
Síntesis de elementos transuranios
El uranio (Z = 92) es el elemento natural más pesado. En consecuencia, todos los elementos con Z > 92, los elementos transuránicos, son artificiales y se han preparado bombardeando núcleos diana adecuados con partículas más pequeñas. El primero de los elementos transuránicos que se prepararon fue el neptunio (Z = 93), el cual se sintetizó en 1940 bombardeando un objetivo de 238 U con neutrones. Como se muestra en la Ecuación 20.21, esta reacción ocurre en dos etapas. Inicialmente, un neutrón se combina con un núcleo de 238 U para formar 239 U, que es inestable y experimenta desintegración beta para producir 239 Np:
\(^{238}_{92}\textrm{U} + \, ^{1}_{0}\textrm{n} \rightarrow \,^{239}_{92}\textrm{U}\rightarrow \,^{239}_{93}\textrm{Np}+\,^{0}_{-1}\beta\label{Eq21}\)
La posterior desintegración beta de 239 Np produce el segundo elemento transuranio, el plutonio (Z = 94):
\(^{239}_{93}\textrm{Np} \rightarrow \,^{239}_{94}\textrm{Pu}+\,^{0}_{-1}\beta\label{Eq22}\)
Bombardear el objetivo con núcleos más masivos crea elementos que tienen números atómicos significativamente mayores que los del núcleo objetivo (Tabla\(\PageIndex{2}\)). Tales técnicas han dado como resultado la creación de los elementos superpesados 114 y 116, los cuales se encuentran en o cerca de la “isla de estabilidad”.
| \(^{239}_{94}\textrm{Pu}+\,^{4}_{2}\alpha \rightarrow \,^{242}_{96}\textrm{Cm}+\,^{1}_{0}\textrm{n}\) |
|---|
| \ (^ {239} _ {94}\ textrm {Pu} +\, ^ {4} _ {2}\ alfa\ fila derecha\, ^ {242} _ {96}\ textrm {Cm} +\, ^ {1} _ {0}\ textrm {n}\)” style="text-align:justify; ">\(^{239}_{94}\textrm{Pu}+\,^{4}_{2}\alpha \rightarrow \,^{241}_{95}\textrm{Am}+\,^{1}_{1}\textrm{p}+\,^{1}_{0}\textrm{n}\) |
| \ (^ {239} _ {94}\ textrm {Pu} +\, ^ {4} _ {2}\ alfa\ fila derecha\, ^ {242} _ {96}\ textrm {Cm} +\, ^ {1} _ {0}\ textrm {n}\)” style="text-align:justify; ">\(^{242}_{96}\textrm{Cm}+\,^{4}_{2}\alpha \rightarrow \,^{243}_{97}\textrm{Bk}+\,^{1}_{1}\textrm{p}+2^{1}_{0}\textrm{n}\) |
| \ (^ {239} _ {94}\ textrm {Pu} +\, ^ {4} _ {2}\ alfa\ fila derecha\, ^ {242} _ {96}\ textrm {Cm} +\, ^ {1} _ {0}\ textrm {n}\)” style="text-align:justify; ">\(^{253}_{99}\textrm{Es}+\,^{4}_{2}\alpha \rightarrow \,^{256}_{101}\textrm{Md}+\,^{1}_{0}\textrm{n}\) |
| \ (^ {239} _ {94}\ textrm {Pu} +\, ^ {4} _ {2}\ alfa\ fila derecha\, ^ {242} _ {96}\ textrm {Cm} +\, ^ {1} _ {0}\ textrm {n}\)” style="text-align:justify; ">\(^{238}_{92}\textrm{U}+\,^{12}_{6}\textrm{C} \rightarrow \,^{246}_{98}\textrm{Cf}+4^{1}_{0}\textrm{n}\) |
| \ (^ {239} _ {94}\ textrm {Pu} +\, ^ {4} _ {2}\ alfa\ fila derecha\, ^ {242} _ {96}\ textrm {Cm} +\, ^ {1} _ {0}\ textrm {n}\)” style="text-align:justify; ">\(^{252}_{98}\textrm{Cf}+\,^{10}_{5}\textrm{B} \rightarrow \,^{256}_{103}\textrm{Lr}+6^{1}_{0}\textrm{n}\) |
Un dispositivo llamado acelerador de partículas se utiliza para acelerar las partículas cargadas positivamente a las velocidades necesarias para superar las repulsiones electrostáticas entre ellas y los núcleos objetivo mediante el uso de campos eléctricos y magnéticos. Operacionalmente, el acelerador de partículas más simple es el acelerador lineal (Figura\(\PageIndex{6}\)), en el que se inyecta un haz de partículas en un extremo de un tubo largo evacuado. La rápida alternancia de la polaridad de los electrodos a lo largo del tubo hace que las partículas se aceleren alternativamente hacia una región de carga opuesta y sean repelidas por una región con la misma carga, lo que resulta en una tremenda aceleración a medida que la partícula viaja por el tubo. Un acelerador lineal moderno como el Acelerador Lineal de Stanford (SLAC) en la Universidad de Stanford tiene aproximadamente 2 millas de largo.
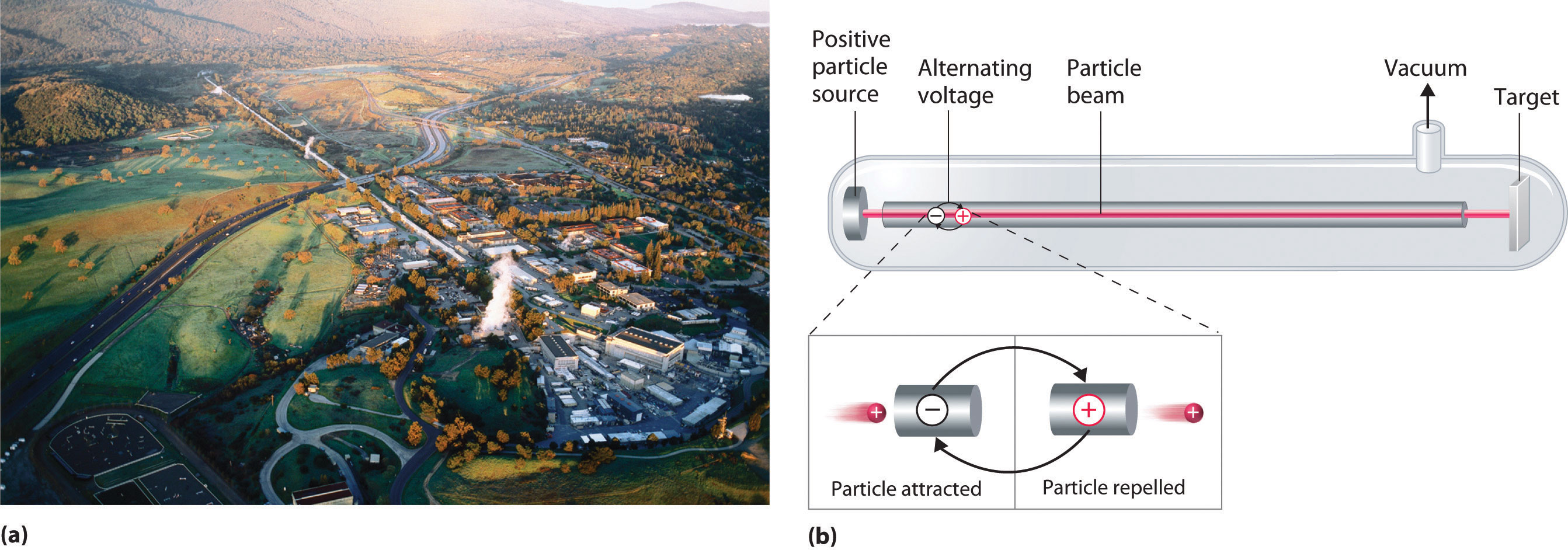
Para lograr el mismo resultado en menos espacio, un acelerador de partículas llamado ciclotrón obliga a las partículas cargadas a viajar en una trayectoria circular en lugar de una lineal. Las partículas se inyectan en el centro de un anillo y se aceleran alternando rápidamente la polaridad de dos grandes electrodos en forma de D por encima y por debajo del anillo, lo que acelera las partículas hacia afuera a lo largo de una trayectoria en espiral hacia el objetivo.
La longitud de un acelerador lineal y el tamaño de los electrodos en forma de D en un ciclotrón limitan severamente la energía cinética que las partículas pueden alcanzar en estos dispositivos. Estas limitaciones se pueden superar mediante el uso de un sincrotrón, un híbrido de los dos diseños. Un sincrotrón contiene un tubo evacuado similar al de un acelerador lineal, pero el tubo es circular y puede tener más de una milla de diámetro. Las partículas cargadas son aceleradas alrededor del círculo por una serie de imanes cuyas polaridades se alternan rápidamente.
Resumen y llave para llevar
- Las reacciones de desintegración nuclear ocurren espontáneamente en todas las condiciones y producen núcleos hijos más estables, mientras que las reacciones de transmutación nuclear se inducen y forman un núcleo producto que es más masivo que el material de partida.
En las reacciones de desintegración nuclear (o desintegración radiactiva), el núcleo parental se convierte en un núcleo hijo más estable. Los núcleos con demasiados neutrones se descomponen al convertir un neutrón en protón, mientras que los núcleos con muy pocos neutrones se descomponen al convertir un protón en un neutrón. Los núcleos muy pesados (con A ≥ 200 y Z > 83) son inestables y tienden a descomponerse emitiendo una partícula α. Cuando un nucleido inestable sufre desintegración radiactiva, se conserva el número total de nucleones, al igual que la carga positiva total. Se conocen seis tipos diferentes de reacciones de desintegración nuclear. La desintegración alfa da como resultado la emisión de una partícula α\(^4 _2 \alpha\),, y produce un núcleo hijo con un número de masa que es menor en 4 y un número atómico que es menor en 2 que el núcleo padre. La desintegración beta convierte un neutrón en protón y emite un electrón de alta energía, produciendo un núcleo hijo con el mismo número de masa que el padre y un número atómico que es mayor en 1. La emisión de positrones es lo opuesto a la desintegración beta y convierte un protón en un neutrón más un positrón. La emisión de positrones no cambia el número de masa del núcleo, pero el número atómico del núcleo hijo es menor en 1 que el progenitor. En la captura de electrones (EC), un electrón en una capa interna reacciona con un protón para producir un neutrón, con emisión de una radiografía. El número de masa no cambia, pero el número atómico de la hija es menor en 1 que el padre. En emisión gamma, un núcleo hijo en estado excitado nuclear experimenta una transición a un estado de menor energía al emitir un rayo γ. Núcleos muy pesados con altas proporciones neutrón-protón pueden sufrir fisión espontánea, en la que el núcleo se rompe en dos piezas que pueden tener diferentes números atómicos y masas atómicas con la liberación de neutrones. Muchos núcleos muy pesados se descomponen a través de una serie de desintegración radiactiva, una sucesión de alguna combinación de alfa- y reacciones de desintegración beta. En las reacciones de transmutación nuclear, un núcleo objetivo es bombardeado con partículas subatómicas energéticas para dar un núcleo producto que es más masivo que el original. Todos los elementos transuránicos —elementos con Z > 92— son artificiales y deben prepararse mediante reacciones de transmutación nuclear. Estas reacciones se llevan a cabo en aceleradores de partículas como aceleradores lineales, ciclotrones y sincrotrones.
Ecuaciones Clave
desintegración alfa
\[^A_Z \textrm X\rightarrow \, ^{A-4}_{Z-2} \textrm X'+\,^4_2 \alpha \nonumber \]
decaimiento beta
\[^A_Z \textrm X\rightarrow \, ^{A}_{Z+1} \textrm X'+\,^0_{-1} \beta \nonumber \]
emisión de positrones
\[^A_Z \textrm X\rightarrow \, ^{A}_{Z-1} \textrm X'+\,^0_{+1} \beta \nonumber \]
captura de electrones
\[^A_Z \textrm X+\,^{0}_{-1} \textrm e\rightarrow \, ^{A}_{Z-1} \textrm X'+\textrm{x-ray} \nonumber \]
emisión gamma
\[^A_Z \textrm{X*}\rightarrow \, ^{A}_{Z} \textrm X+\,^0_{0} \gamma \nonumber \]

