6.2: Estructura Electrónica de Complejos (Parte 1)

Es necesario aprender algunos conceptos para comprender la estructura, el espectro, el magnetismo y la reactividad de los complejos que dependen de las configuraciones de d electrones. En particular, la teoría de la estructura electrónica es importante.

Teoría del campo de ligandos

La teoría del campo de ligandos es una de las teorías más útiles para dar cuenta de la estructura electrónica de los complejos. Se originó en la aplicación de la teoría del campo cristalino de los cristales iónicos a sistemas complejos metálicos.

Seis complejos octaédricos coordinados

Los orbitales de cinco d de los cationes de metales de transición son degenerados y tienen igual energía.

Figura\(\PageIndex{4}\): Cambio de la energía electrónica tras la formación compleja.

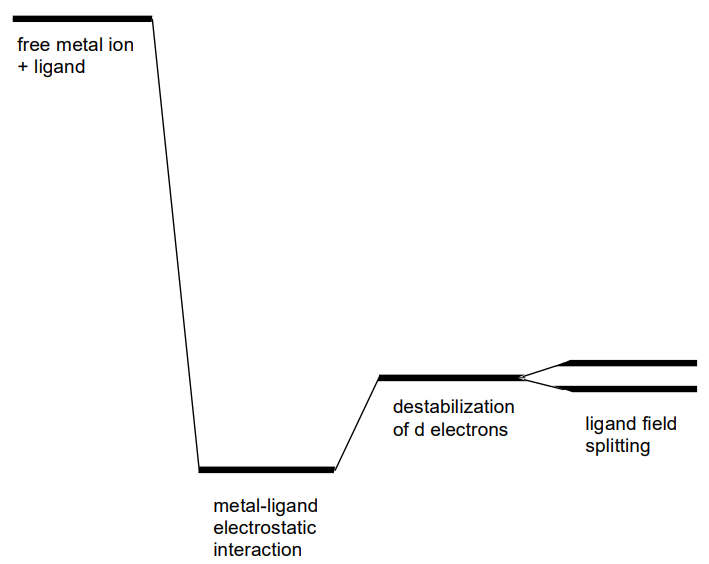
El campo eléctrico negativo esférico alrededor de un catión metálico da como resultado que el nivel de energía total sea menor que el de un catión libre debido a las interacciones electrostáticas. La interacción repulsiva entre los electrones en los orbitales metálicos y el campo eléctrico negativo desestabiliza el sistema y compensa en cierta medida la estabilización (Figura\(\PageIndex{4}\)).

Figura\(\PageIndex{5}\): Posiciones del ligando en la coordenada cartesiana con un ion metálico en el origen.

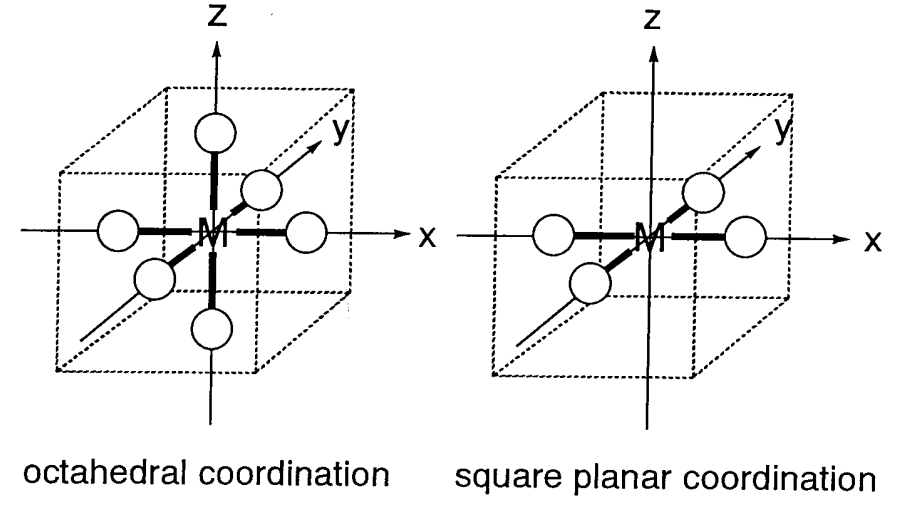
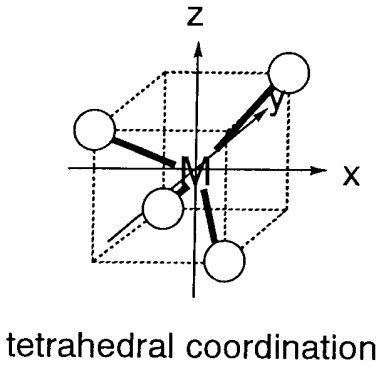
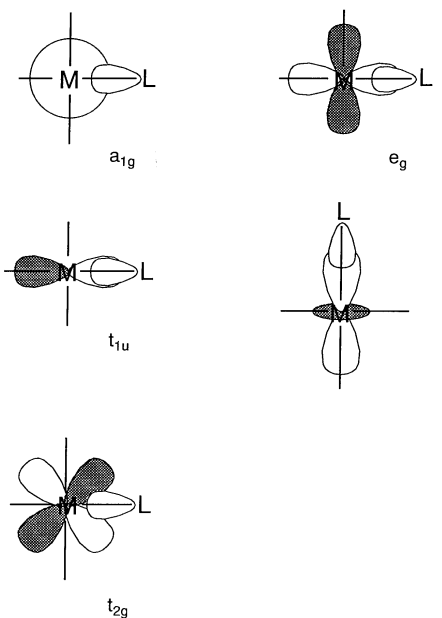
Supongamos que en lugar de un campo negativo esférico uniforme, el campo es generado por seis ligandos que se coordinan octaédricamente con un metal central. El campo negativo de los ligandos se denomina campo de ligandos. La carga negativa, en el caso de ligandos aniónicos, o un extremo negativo (par solitario), en el caso de ligandos neutros, ejercen una fuerza repulsiva sobre los orbitales metálicos d que es anisotrópica dependiendo de la dirección de los orbitales. La posición del catión metálico se toma como origen y se construyen las coordenadas cartesianas (Figura\(\PageIndex{5}\)). Luego, los orbitales d _{x ² -y} 2 y d _{z ²} se alinean a lo largo de las direcciones de los ejes y los orbitales d _xy, d _{yz y d xz} se dirigen entre los ejes. Si se colocan ligandos en los ejes, la interacción repulsiva es mayor para los orbitales eg (d _{x ² -y ²}, d _{z ²}) que para los orbitales t _2g (d _xy, d _yz, d _xz), y el e _g los orbitales se desestabilizan y los orbitales t _2g se estabilizan en igual medida. En la siguiente discusión, solo es esencial la diferencia de energía entre los orbitales t _2g y e _g y la energía promedio de estos orbitales se toma como el cero de energía. Si la diferencia de energía entre los dos orbitales e _g y tres t _2g se establece en\(\Delta_{o}\), el nivel de energía de los orbitales eg es +3/5\(\Delta_{o}\) y el de los orbitales t _2g es -2/5\(\Delta_{o}\) (Figura\(\PageIndex{6}\)). (también se\(\Delta_{o}\) puede expresar como 10 Dq. En este caso, el nivel de energía de los orbitales eg es +6 Dq y el de los orbitales t _2g -4 Dq.)

Figura\(\PageIndex{6}\): División del campo de ligandos en complejos tetraédricos y octaédricos.

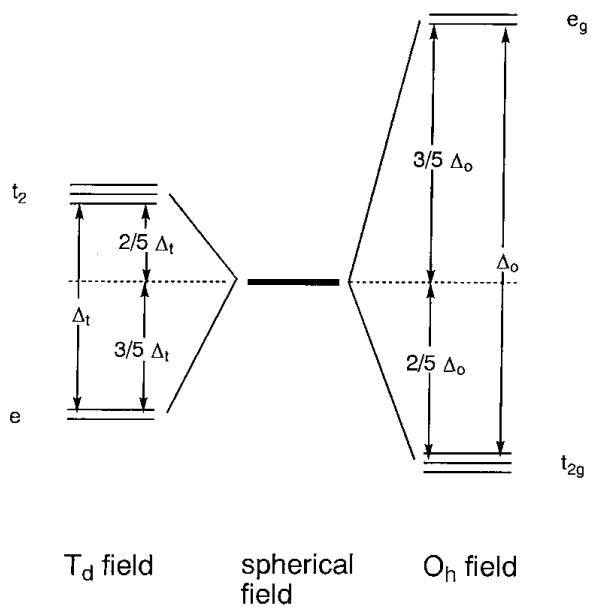
Los iones de metales de transición tienen electrones de 0 a 10 d y cuando los orbitales d divididos se llenan desde un nivel de energía más bajo, se obtiene la configuración de electrones t _2g ^x e _g ^y correspondiente a cada ion. Con el nivel de energía cero elegido como el nivel de energía promedio, la energía de la configuración de electrones en relación con la energía cero se vuelve

\[LFSE = (-0.4x + 0.6y) \Delta_{o}\]

Este valor se denomina energía de estabilización del campo del ligando. La configuración electrónica con menor valor (teniendo en cuenta el signo menos) es más estable. LFSE es un parámetro importante para explicar algunas propiedades de los complejos de metales de transición de bloque d.

Se requiere una condición distinta al nivel de energía orbital para explicar el llenado de electrones que se están poblando en los orbitales divididos t _2g y e _g,. Dos electrones pueden ocupar un orbital con espines antiparalelos pero se produce una fuerte repulsión electrostática entre dos electrones en el mismo orbital. Esta interacción repulsiva se llama energía de emparejamiento, P.

Cuando el número de electrones d es menor a tres, la energía de emparejamiento se minimiza cargando los electrones en el orbital t _2g con espines paralelos. A saber, las configuraciones de electrones que surgen son t _2g ¹, t _2g ² o t _2g ³.

Dos posibilidades surgen cuando el cuarto electrón ocupa cualquiera de los orbitales t _2g o e _g. El orbital de menor energía t _2g es favorable pero la ocupación del mismo orbital da lugar a la energía de apareamiento, P. La energía total se vuelve

\[-0.4 \Delta_{o} \times 4 + P = - 1.6 \Delta_{o} + P\]

Si el cuarto electrón ocupa el orbital energéticamente desfavorable e _g, la energía total se vuelve

\[-0.4 \Delta_{o} \times 3 + 0.6 \Delta-{o} = - 0.6 \Delta_{o}\]

La elección de la configuración electrónica depende de cuál de los valores anteriores sea mayor. Por lo tanto, si\(\Delta_{o}\) > P, t _2g ⁴ es favorecido y esto se llama el caso de campo fuerte o la configuración de electrones de espín bajo. Si\(\Delta_{o}\) < P, t _2g ³ e _g ¹ es favorecido y esto se llama el caso de campo débil o la configuración de electrones de espín alto. Se requiere una elección similar para los complejos octaédricos d ⁵, d ⁶ y d ⁷, y en el caso de campo fuerte, las configuraciones t _{2g ⁵, t 2g} ⁶ o t _2g ⁶ e _g ¹ son favorecieron, mientras que en el caso de campo débil, se favorecen las configuraciones t _2g ³ e _g ², t _{2g ⁴ e g 2, o t 2g e g} ². El parámetro de división del campo del ligando\(\Delta_{o}\) se decide por la naturaleza de los ligandos y el metal, mientras que la energía de emparejamiento, P, es casi constante y muestra solo una ligera dependencia de la identidad del metal.

Complejos planos cuadrados

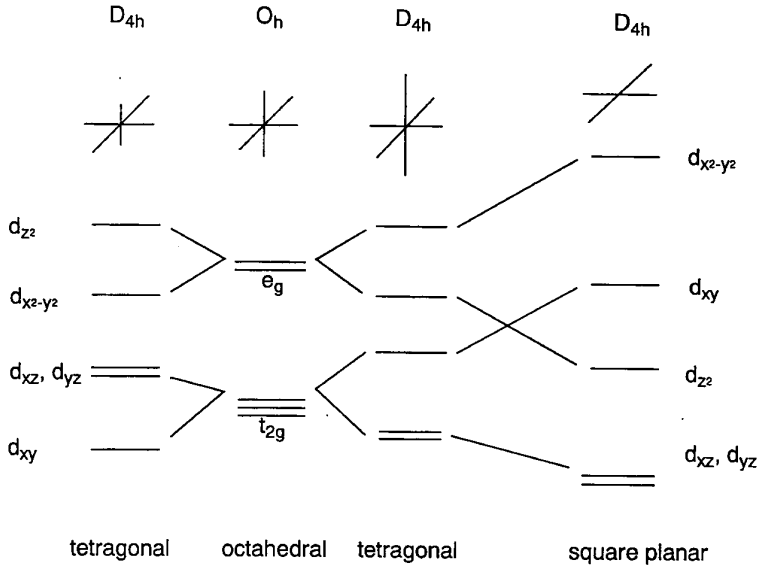
Los complejos con cuatro ligandos en un plano que contiene el metal central se denominan complejos planos cuadrados. Es más fácil comprender los niveles de energía electrónica de los orbitales d en complejos planos cuadrados partiendo de los de los complejos octaédricos hexacoordinados. Colocando los seis ligandos a lo largo de los ejes cartesianos, los dos ligandos en el eje z se eliminan gradualmente del metal central y finalmente solo quedan cuatro ligandos en el plano x, y. La interacción de los dos ligandos de coordenadas z con los orbitales d _{z ²}, d _xz y d _yz se vuelve más pequeña y los niveles de energía de estos ligandos disminuyen. Por otro lado, los cuatro ligandos restantes se acercan al metal y los niveles de energía d _{x ^{2 -y 2}} y d _xy suben como resultado de la eliminación de los dos ligandos. Esto da como resultado que el orden de los niveles de energía de cinco d orbitales sea d _xz, d _yz < d _{z ²} < d _xy << d _{x ² -y ²} (Figura\(\PageIndex{7}\)). Los complejos Rh ^{+, Ir +}, Pd ²⁺, Pt ^{2 +} y Au ³⁺ con una configuración d ⁸ tienden a formar estructuras planas cuadradas porque ocho electrones ocupan los orbitales inferiores dejando el mayor d _{x ² -y} ² orbitales vacíos.

Figura\(\PageIndex{7}\): Cambio de la energía orbital de complejos octaédricos a planos cuadrados.

Complejos tetraédricos

Los complejos tetraédricos tienen cuatro ligandos en los ápices de un tetraedro alrededor del metal central. [CoX ₄] ^2- (X = Cl, Br, I), Ni (CO) ₄, etc. son todos ejemplos de complejos de 4-coordinación (Figura\(\PageIndex{5}\)). Cuando se coloca un metal sobre el origen de los ejes cartesianos, como en los complejos octaédricos, e orbitales (d _{x ² -y ²}, d _{z ²}) están distantes de los ligandos y t ₂ orbitales (d _xy, d _yz, d _xz) están más cerca ligandos. En consecuencia, la repulsión electrónica es mayor para los orbitales t ₂, los cuales se desestabilizan en relación con los orbitales e. El campo de ligandos ejercido por cuatro ligandos divide los orbitales degenerados cinco veces del metal central en dos conjuntos degenerados e y tres veces degenerados t ₂ (Figura\(\PageIndex{6}\)). El conjunto t ₂ tiene energía de +2/5\(\Delta_{t}\) y el conjunto e -3/5\(\Delta_{t}\) con una división de campo de ligando de\(\Delta_{t}\). Como el número de ligandos es 4/6 = 2/3 del de los complejos octaédricos hexacoordinados, y el solapamiento de los ligandos con los orbitales es menor, y la división del ligando\(\Delta_{t}\) es aproximadamente la mitad de\(\Delta_{o}\). En consecuencia, solo se conocen configuraciones de electrones de alto espín en los complejos tetraédricos. Las energías de división del campo del ligando calculadas por el método anterior se muestran en la Tabla\(\PageIndex{2}\).

Tabla Energía de estabilización de campo de\(\PageIndex{2}\) ligando (LFSE)

		Octaédrica				Tetraédrico
		Campo fuerte (LS)		Campo débil (HS)
d ^n	Ejemplo	n	\(\Delta_{o}\)	n	\(\Delta_{o}\)	n	\(\Delta_{t}\)
d ^1	Ti ^3 ^+	1	0.4	1	0.4	1	0.6
d ^2	V ^3+	2	0.8	2	0.8	2	1.2
d ^3	Cr ^3 ^+, V ^2+	3	1.2	3	1.2	3	0.8
d ^4	Cr ^2+, Mn ^3 ^+	2	1.6	4	0.6	4	0.4
d ^5	Mn ^2 ^+, Fe ^3+	1	2.0	5	0	5	0
d ^6	Fe ^2 ^+, Co ^3+	0	2.4	4	0.4	4	0.6
d ^7	Co ^2 ^+	1	1.8	3	0.8	3	1.2
d ^8	Ni ^2 ^+	2	1.2	2	1.2	2	0.8
d ^9	Cu ^2 ^+	1	0.6	1	0.6	1	0.4
d ^10	Cu ^1+	0	0	0	0	0	0

Efecto Jahn-Teller

Cuando los orbitales de una molécula poliatómica no lineal altamente simétrica son degenerados, la degeneración se resuelve distorsionando el marco molecular para lograr una simetría más baja y, por lo tanto, una menor energía. Este es el efecto Jahn-Teller y se observa un ejemplo típico en la distorsión tetragonal de una estructura de coordinación octaédrica de complejos hexacoordinados de Cu ^{2 +}.

Figura\(\PageIndex{8}\): Separación de Jahn-Teller en un ion Cu ²⁺.

Figura\(\PageIndex{9}\): Relación entre los orbitales de metal y ligando durante la formación de\(\sigma\) enlaces.

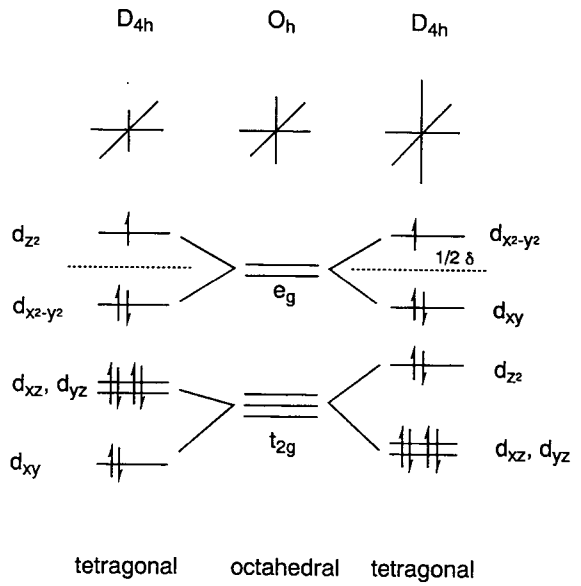
Tienen configuraciones d ⁹ y los orbitales e _g en la estructura octaédrica están ocupados por tres electrones. Si los orbitales e _g se dividen y dos electrones ocupan el orbital inferior y un electrón el orbital superior, el sistema gana energía de la mitad de la diferencia de energía,\(\delta\), de dos orbitales divididos. Por lo tanto, una distorsión tetragonal en el eje z se vuelve favorable.