2.8: Resolver desigualdades de valores absolutos
- Page ID
- 51812
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, usted será capaz de:
- Resolver ecuaciones de valor absoluto
- Resuelve desigualdades de valor absoluto con “menos que”
- Resolver desigualdades de valor absoluto con “mayor que”
- Resolver aplicaciones con valor absoluto
Antes de comenzar, toma este cuestionario de preparación.
- Evaluar: \(−|7|\).
Si te perdiste este problema, revisa [link]. - Rellene \(<,>,<,>,\) o \(=\) para cada uno de los siguientes pares de números.
ⓐ \(|−8|\text{___}−|−8|\) ⓑ \(12\text{___}−|−12|\) ⓒ \(|−6|\text{___}−6\) ⓓ \(−(−15)\text{___}−|−15|\)
Si te perdiste este problema, revisa [link]. - Simplificar: \(14−2|8−3(4−1)|\).
Si te perdiste este problema, revisa [link].
Resolver ecuaciones de valor absoluto
A medida que nos preparamos para resolver ecuaciones de valor absoluto, revisamos nuestra definición de valor absoluto.
El valor absoluto de un número es su distancia desde cero en la línea numérica.
El valor absoluto de un número n se escribe como \(|n|\) y \(|n|\geq 0\) para todos los números.
Los valores absolutos son siempre mayores o iguales a cero.
Aprendimos que tanto un número como su opuesto están a la misma distancia de cero en la línea numérica. Dado que tienen la misma distancia de cero, tienen el mismo valor absoluto. Por ejemplo:
- \(−5\) está a 5 unidades de distancia de 0, por lo que \(|−5|=5\).
- \(5\) está a 5 unidades de distancia de 0, por lo que \(|5|=5\).
La figura \(\PageIndex{1}\) ilustra esta idea.
Para la ecuación |x|=5, |x|=5, estamos buscando todos los números que hagan de esta una declaración verdadera. Estamos buscando los números cuya distancia desde cero es 5. Acabamos de ver que tanto 5 como −5−5 son cinco unidades desde cero en la línea numérica. Ellos son las soluciones a la ecuación.
\(\begin{array} {ll} {\text{If}} &{|x|=5} \\ {\text{then}} &{x=−5\text{ or }x=5} \\ \end{array}\)
La solución se puede simplificar a una sola declaración por escrito \(x=\pm 5\). Se lee esto, “x es igual a positivo o negativo 5”.
Podemos generalizar esto a la siguiente propiedad para ecuaciones de valor absoluto.
Para cualquier expresión algebraica, u, y cualquier número real positivo, a,
\[\begin{array} {ll} {\text{if}} &{|u|=a} \\ {\text{then}} &{u=−a \text{ or }u=a} \\ \nonumber \end{array}\]
Recuerda que un valor absoluto no puede ser un número negativo.
Resolver:
- \(|x|=8\)
- \(|y|=−6\)
- \(|z|=0\)
- Solución a
-
\(\begin{array} {ll} {} &{|x|=8} \\ {\text{Write the equivalent equations.}} &{x=−8 \text{ or } x=8} \\ {} &{x=\pm 8} \\ \end{array}\)
- Solución b
-
\(\begin{array} {ll} {} &{|y|=−6} \\ {} &{\text{No solution}} \\ \end{array}\)
Dado que un valor absoluto es siempre positivo, no hay soluciones a esta ecuación. - Solución c
-
\(\begin{array} {ll} {} &{|z|=0} \\ {\text{Write the equivalent equations.}} &{z=−0\text{ or }z=0} \\ {\text{Since }−0=0,} &{z=0} \\ \end{array}\)
Ambas ecuaciones nos dicen que z=0z=0 y así solo hay una solución.
Resolver:
- \(|x|=2\)
- \(|y|=−4\)
- \(|z|=0\)
- Contesta a
-
\(\pm 2\)
- Respuesta b
-
no hay solución
- Respuesta c
-
0
Resolver:
- \(|x|=11\)
- \(|y|=−5\)
- \(|z|=0\)
- Contesta a
-
\(\pm 11\)
- Respuesta b
-
no hay solución
- Respuesta c
-
0
Para resolver una ecuación de valor absoluto, primero aislamos la expresión del valor absoluto utilizando los mismos procedimientos que usamos para resolver ecuaciones lineales. Una vez que aislamos la expresión del valor absoluto la reescribimos como las dos ecuaciones equivalentes.
Cómo resolver ecuaciones de valor absoluto
Resolver \(|5x−4|−3=8\).
- Solución
-
Resolver: \(|3x−5|−1=6\).
- Contestar
-
\(x=4, \space x=−\frac{2}{3}\)
Resolver: \(|4x−3|−5=2\).
- Contestar
-
\(x=−1,\space x=\frac{5}{2}\)
Los pasos para resolver una ecuación de valor absoluto se resumen aquí.
- Aislar la expresión de valor absoluto.
- Escribe las ecuaciones equivalentes.
- Resuelve cada ecuación.
- Revisa cada solución.
Resolver \(2|x−7|+5=9\).
- Solución
-
\(2|x−7|+5=9\) Aislar la expresión de valor absoluto. \(2|x−7|=4\) \(|x−7|=2\) Escribe las ecuaciones equivalentes. \(x−7=−2\) o \(x−7=2\) Resuelve cada ecuación. \(x=5\) o \(x=9\) Chequear:
Resolver: \(3|x−4|−4=8\).
- Contestar
-
\(x=8,\space x=0\)
Resolver: \(2|x−5|+3=9\).
- Contestar
-
\(x=8,\space x=2\)
Recuerda, ¡un valor absoluto siempre es positivo!
Resolver: \(|\frac{2}{3}x−4|+11=3\).
- Solución
-
\(\begin{array} {ll} {} &{|\frac{2}{3}x−4|=−8} \\ {\text{Isolate the absolute value term.}} &{|\frac{2}{3}x−4|=−8} \\ {\text{An absolute value cannot be negative.}} &{\text{No solution}} \\ \end{array}\)
Resolver: \(|\frac{3}{4}x−5|+9=4\).
- Contestar
-
Sin solución
Resolver: \(|\frac{5}{6}x+3|+8=6\).
- Contestar
-
Sin solución
Algunas de nuestras ecuaciones de valor absoluto podrían ser de la forma \(|u|=|v|\) donde u y v son expresiones algebraicas. Por ejemplo, \(|x−3|=|2x+1|\).
¿Cómo los resolveríamos? Si dos expresiones algebraicas son iguales en valor absoluto, entonces son iguales entre sí o negativas entre sí. La propiedad para ecuaciones de valor absoluto dice que para cualquier expresión algebraica, u, y un número real positivo, a, if \(|u|=a\), entonces \(u=−a\) o \(u=a\).
Esto nos dice que
\ (\ begin {array} {llll}
{\ texto {if}} & {|u|=|v|} & {} & {} & {}
\ {\ texto {entonces}} & {|u|=v} & {\ text {o}} & {|u|=−v}
\\ {\ text {and so}} & {u=v\ text {o} u = −v} & {\ text {or}} & {u=−v\ text {o} u = − (−v)}
\\ end {array}\)
Esto nos lleva a la siguiente propiedad para ecuaciones con dos valores absolutos.
Para cualquier expresión algebraica, u y v ,
\[\begin{array} {ll} {\text{if}} &{|u|=|v|} \\ {\text{then}} &{u=−v\text{ or }u=v} \\ \nonumber \end{array}\]
Cuando tomamos lo contrario de una cantidad, debemos tener cuidado con los signos y agregar paréntesis donde sea necesario.
Resolver: \(|5x−1|=|2x+3|\).
- Solución
-
\(\begin{array} {ll} {} &{} &{|5x−1|=|2x+3|} &{} \\ {} &{} &{} &{} \\ {\text{Write the equivalent equations.}} &{5x−1=−(2x+3)} &{\text{or}} &{5x−1=2x+3} \\ {} &{5x−1=−2x−3} &{\text{or}} &{3x−1=3} \\ {\text{Solve each equation.}} &{7x−1=−3} &{} &{3x=4} \\ {} &{7x=−2} &{} &{x=43} \\ {} &{x=−27} &{\text{or}} &{x=43} \\ {\text{Check.}} &{} &{} &{} \\ {\text{We leave the check to you.}} &{} &{} &{} \\ \end{array}\)
Resolver: \(|7x−3|=|3x+7|\).
- Contestar
-
\(x=−\frac{2}{5}, \space x=\frac{5}{2}\)
Resolver: \(|6x−5|=|3x+4|\).
- Contestar
-
\(x=3, x=19\)
Resuelve Desigualdades de Valor Absoluto con “Menos Que”
Veamos ahora lo que sucede cuando tenemos una desigualdad de valores absolutos. Todo lo que hemos aprendido sobre la solución de desigualdades sigue vigente, pero debemos considerar cómo impacta el valor absoluto en nuestro trabajo. Nuevamente veremos nuestra definición de valor absoluto. El valor absoluto de un número es su distancia desde cero en la línea numérica. Para la ecuación \(|x|=5\), vimos que tanto 5 como \(−5\) son cinco unidades desde cero en la línea numérica. Ellos son las soluciones a la ecuación.
\[\begin{array} {lll} {} &{|x|=5} &{} \\ {x=−5} &{\text{or}} &{x=5} \\ \nonumber \end{array}\]
¿Qué pasa con la desigualdad \(|x|\leq 5\)? ¿Dónde están los números cuya distancia es menor o igual a 5? Sabemos \(−5\) y 5 son ambas cinco unidades de cero. Todos los números entre \(−5\) y 5 son menos de cinco unidades a partir de cero (Figura \(\PageIndex{2}\)).
De una manera más general, podemos ver que si \(|u|\leq a\), entonces \(−a\leq u\leq a\) (Figura \(\PageIndex{3}\)).
Este resultado se resume aquí.
Para cualquier expresión algebraica, u, y cualquier número real positivo, a,
\[ \text{if} \quad |u|<a, \quad \text{then} \space −a<u<a \\ \text{if} \quad |u|\leq a, \quad \text{then} \space−a\leq u\leq a \nonumber\]
Después de resolver una desigualdad, a menudo es útil revisar algunos puntos para ver si la solución tiene sentido. La gráfica de la solución divide la línea numérica en tres secciones. Elige un valor en cada sección y sumértalo en la desigualdad original para ver si hace que la desigualdad sea verdadera o no. Si bien esta no es una comprobación completa, a menudo ayuda a verificar la solución.
Resolver \(|x|<7\). Grafica la solución y escribe la solución en notación de intervalos.
- Solución
-
Escribe la desigualdad equivalente. Grafica la solución. Escribe la solución usando notación de intervalos. Comprobar:
Para verificar, verifique un valor en cada sección de la línea numérica que muestre la solución. Elija números como −8, −8, 1 y 9.
Grafica la solución y escribe la solución en notación de intervalos: \(|x|<9\).
- Contestar
-
Grafica la solución y escribe la solución en notación de intervalos: \(|x|<1\).
- Contestar
-
Resolver \(|5x−6|\leq 4\). Grafica la solución y escribe la solución en notación de intervalos.
- Solución
-
Paso 1. Aislarla expresión de valor absoluto.
Está aislado.\(|5x−6|\leq 4\) Paso 2. Escribela desigualdad compuesta equivalente. \(−4\leq 5x−6\leq 4\) Paso 3. Resolverla desigualdad compuesta. \(2\leq 5x\leq 10\)
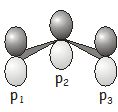
\(\frac{2}{5}\leq x\leq 2\)Paso 4. Graficala solución. 
Paso 5. Escribela solución usando notación de intervalos. \([\frac{2}{5}, 2]\)
Cheque: El cheque se deja a usted.
Resolver \(|2x−1|\leq 5\). Grafica la solución y escribe la solución en notación de intervalos:
- Contestar
-
Resolver \(|4x−5|\leq 3\). Grafica la solución y escribe la solución en notación de intervalos:
- Contestar
-
- Aislar la expresión de valor absoluto.
- Escribe la desigualdad compuesta equivalente.
\[\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{−a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{−a\leq u\leq a} \\ \nonumber \end{array}\]
- Resolver la desigualdad compuesta.
- Grafica la solución
- Escribe la solución usando notación de intervalos.
Resuelve Desigualdades de Valor Absoluto con “Mayor que”
¿Qué sucede con las desigualdades de valor absoluto que tienen “mayor que”? Nuevamente veremos nuestra definición de valor absoluto. El valor absoluto de un número es su distancia desde cero en la línea numérica.
Empezamos con la desigualdad \(|x|\leq 5\). Vimos que los números cuya distancia es menor o igual a cinco desde cero en la línea numérica eran \(−5\) y 5 y todos los números entre \(−5\) y 5 (Figura \(\PageIndex{4}\)).
Ahora queremos mirar la desigualdad \(|x|\geq 5\). ¿Dónde están los números cuya distancia desde cero es mayor o igual a cinco?
Nuevamente ambos \(−5\) y 5 son cinco unidades desde cero y así se incluyen en la solución. Los números cuya distancia desde cero es mayor que cinco unidades serían menores \(−5\) y mayores que 5 en la línea numérica (Figura \(\PageIndex{5}\)).
De una manera más general, podemos ver que si \(|u|\geq a\), entonces \(u\leq −a\) o \(u\leq a\). Ver Figura.
Este resultado se resume aquí.
Para cualquier expresión algebraica, u, y cualquier número real positivo, a,
\[\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\quad \text{then } u<−a \text{ or } u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\quad \text{then } u\leq −a \text{ or } u\geq a} \\ \nonumber \end{array}\]
Resolver \(|x|>4\). Grafica la solución y escribe la solución en notación de intervalos.
- Solución
-
\(|x|>4\) Escribe la desigualdad equivalente. \(x<−4\) o \(x>4\) Grafica la solución. 
Escribe la solución usando notación de intervalos. \((−\inf ,−4)\cup (4,\inf )\) Comprobar: Para verificar, verifique un valor en cada sección de la línea numérica que muestre la solución. Elija números como −6, −6, 0 y 7.
Resolver \(|x|>2\). Grafica la solución y escribe la solución en notación de intervalos.
- Contestar
-
Resolver \(|x|>1\). Grafica la solución y escribe la solución en notación de intervalos.
- Contestar
-
Resolver \(|2x−3|\geq 5\). Grafica la solución y escribe la solución en notación de intervalos.
- Solución
-
\(|2x−3|\geq 5\) Paso 1. Aislarla expresión de valor absoluto. Está aislado. Paso 2. Escribela desigualdad compuesta equivalente. \(2x−3\leq −5\) o \(2x−3\geq 5\) Paso 3. Resolverla desigualdad compuesta. \(2x\leq −2\) o \(2x\geq 8\)
\(x\leq −1\) o \(x\geq 4\)Paso 4. Graficala solución. 
Paso 5. Escribela solución usando notación de intervalos. \((−\inf ,−1]\cup [4,\inf )\)
Cheque: El cheque se deja a usted.
Resolver \(|4x−3|\geq 5\). Grafica la solución y escribe la solución en notación de intervalos.
- Contestar
-
Resolver \(|3x−4|\geq 2\). Grafica la solución y escribe la solución en notación de intervalos.
- Contestar
-
- Aislar la expresión de valor absoluto.
- Escribe la desigualdad compuesta equivalente.
\ [\ begin {array} {lll}
{|u| >a} & {\ quad\ text {es equivalente a}} & {u<−a\ quad\ texto {o}\ quad u>a}
\\ {|u|\ geq a} & {\ quad\ text {es equivalente a}} & {u\ leq −a\ quad\ text {o}\ quad u\ geq a}
\\ {|u| >a} & {\ quad\ text {es equivalente a}} & {u<−a\ quad\ text {o}\ quad u>a}
\\ {|u|\ geq a} & {\ quad\ text {es equivalente a}} & {u\ leq −a\ quad\ text {o}\ quad u\ geq a}
\\\ nonumber\ end {array}\] - Resolver la desigualdad compuesta.
- Grafica la solución
- Escribe la solución usando notación de intervalos.
Resolver aplicaciones con valor absoluto
Las desigualdades de valor absoluto se utilizan a menudo en el proceso de fabricación. Se debe hacer un artículo con especificaciones casi perfectas. Por lo general hay una cierta tolerancia de la diferencia con respecto a las especificaciones que se permite. Si la diferencia con respecto a las especificaciones excede la tolerancia, se rechaza el artículo.
\[|\text{actual-ideal}|\leq \text{tolerance} \nonumber\]
El diámetro ideal de una varilla necesaria para una máquina es de 60 mm. El diámetro real puede variar del diámetro ideal por \(0.075\) mm. ¿Qué rango de diámetros será aceptable para el cliente sin que se rechace la varilla?
- Solución
-
\(\begin{array} {ll} {} &{\text{Let }x=\text{ the actual measurement}} \\ {\text{Use an absolute value inequality to express this situation.}} &{|\text{actual-ideal}|\leq \text{tolerance}} \\ {} &{|x−60|\leq 0.075} \\ {\text{Rewrite as a compound inequality.}} &{−0.075\leq x−60\leq 0.075} \\ {\text{Solve the inequality.}} &{59.925\leq x\leq 60.075} \\ {\text{Answer the question.}} &{\text{The diameter of the rod can be between}} \\ {} &{59.925 mm \text{ and } 60.075 mm.} \\ \end{array}\)
El diámetro ideal de una varilla necesaria para una máquina es de 80 mm. El diámetro real puede variar del diámetro ideal en 0.009 mm. ¿Qué rango de diámetros será aceptable para el cliente sin que se rechace la varilla?
- Contestar
-
El diámetro de la varilla puede estar entre 79.991 y 80.009 mm.
El diámetro ideal de una varilla necesaria para una máquina es de 75 mm. El diámetro real puede variar del diámetro ideal en 0.05 mm. ¿Qué rango de diámetros será aceptable para el cliente sin que se rechace la varilla?
- Contestar
-
El diámetro de la varilla puede estar entre 74.95 y 75.05 mm.
Acceda a este recurso en línea para instrucción adicional y práctica con la solución de ecuaciones lineales de valores absolutos y desigualdades.
- Resolver ecuaciones y desigualdades lineales de valores absolutos
Conceptos Clave
- Valor Absoluto
El valor absoluto de un número es su distancia desde 0 en la línea numérica.
El valor absoluto de un número n se escribe como \(|n|\) y \(|n|\geq 0\) para todos los números.
Los valores absolutos son siempre mayores o iguales a cero. - Ecuaciones de Valor Absoluto
Para cualquier expresión algebraica, u, y cualquier número real positivo, a,
\(\begin{array} {ll} {\text{if}} &{\quad |u|=a} \\ {\text{then}} &{\quad u=−a \text{ or } u=a} \\ \end{array}\)
Recuerda que un valor absoluto no puede ser un número negativo. - Cómo Resolver Ecuaciones de Valor Absoluto
- Aislar la expresión de valor absoluto.
- Escribe las ecuaciones equivalentes.
- Resuelve cada ecuación.
- Revisa cada solución.
- Ecuaciones con dos valores absolutos
Para cualquier expresión algebraica, uy v,
\(\begin{array} {ll} {\text{if}} &{\quad |u|=|v|} \\ {\text{then}} &{\quad u=−v \text{ or } u=v} \\ \end{array}\) - Desigualdades de Valor Absoluto con \(<\) o \(\leq\)
Para cualquier expresión algebraica, u , y cualquier número real positivo, a ,
\(\begin{array} {llll} {\text{if}} &{\quad |u|=a} &{\quad \text{then}} &{−a<u<a} \\ {\text{if}} &{\quad |u|\leq a} &{\quad \text{then}} &{−a\leq u\leq a} \\ \end{array}\) - Cómo Resolver Desigualdades de Valor Absoluto con \(<\) o \(\leq\)
- Aislar la expresión de valor absoluto.
- Escribe la desigualdad compuesta equivalente.
\(\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{\quad −a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{\quad −a\leq u\leq a} \\ \end{array}\) - Resolver la desigualdad compuesta.
- Grafica la solución
- Escribir la solución usando notación de intervalos
- Desigualdades de Valor Absoluto con \(>\) o \(\geq\)
Para cualquier expresión algebraica, u , y cualquier número real positivo, a ,
\(\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\text{then } u<−a\text{ or }u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\text{then } u\leq −a\text{ or }u\geq a} \\ \end{array}\) - Cómo Resolver Desigualdades de Valor Absoluto con \(>\) o \(\geq\)
- Aislar la expresión de valor absoluto.
- Escribe la desigualdad compuesta equivalente.
\(\begin{array} {lll} {|u|>a} &{\quad \text{is equivalent to}} &{\quad u<−a\text{ or }u>a} \\ {|u|\geq a} &{\quad \text{is equivalent to}} &{\quad u\leq −a\text{ or }u\geq a} \\ \end{array}\) - Resolver la desigualdad compuesta.
- Grafica la solución
- Escribir la solución usando notación de intervalos