Capítulo 9 Ejercicios de revisión
- Page ID
- 51789
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ejercicios de revisión de capítulos
Resolver ecuaciones cuadráticas usando la propiedad de raíz cuadrada
En los siguientes ejercicios, resuelve usando la Propiedad Raíz Cuadrada.
- \(y^{2}=144\)
- \(n^{2}-80=0\)
- \(4 a^{2}=100\)
- \(2 b^{2}=72\)
- \(r^{2}+32=0\)
- \(t^{2}+18=0\)
- \(\frac{2}{3} w^{2}-20=30\)
- \(5 c^{2}+3=19\)
- Contestar
-
1. \(y=\pm 12\)
3. \(a=\pm 5\)
5. \(r=\pm 4 \sqrt{2} i\)
7. \(w=\pm 5 \sqrt{3}\)
En los siguientes ejercicios, resuelve usando la Propiedad Raíz Cuadrada.
- \((p-5)^{2}+3=19\)
- \((u+1)^{2}=45\)
- \(\left(x-\frac{1}{4}\right)^{2}=\frac{3}{16}\)
- \(\left(y-\frac{2}{3}\right)^{2}=\frac{2}{9}\)
- \((n-4)^{2}-50=150\)
- \((4 c-1)^{2}=-18\)
- \(n^{2}+10 n+25=12\)
- \(64 a^{2}+48 a+9=81\)
- Contestar
-
1. \(p=-1,9\)
3. \(x=\frac{1}{4} \pm \frac{\sqrt{3}}{4}\)
5. \(n=4 \pm 10 \sqrt{2}\)
7. \(n=-5 \pm 2 \sqrt{3}\)
Resuelve ecuaciones cuadráticas completando el cuadrado
En los siguientes ejercicios, completa la plaza para hacer un trinomio cuadrado perfecto. Después escribe el resultado como un binomial cuadrado.
- \(x^{2}+22 x\)
- \(m^{2}-8 m\)
- \(a^{2}-3 a\)
- \(b^{2}+13 b\)
- Contestar
-
1. \((x+11)^{2}\)
3. \(\left(a-\frac{3}{2}\right)^{2}\)
En los siguientes ejercicios, resuelve completando la plaza.
- \(d^{2}+14 d=-13\)
- \(y^{2}-6 y=36\)
- \(m^{2}+6 m=-109\)
- \(t^{2}-12 t=-40\)
- \(v^{2}-14 v=-31\)
- \(w^{2}-20 w=100\)
- \(m^{2}+10 m-4=-13\)
- \(n^{2}-6 n+11=34\)
- \(a^{2}=3 a+8\)
- \(b^{2}=11 b-5\)
- \((u+8)(u+4)=14\)
- \((z-10)(z+2)=28\)
- Contestar
-
1. \(d=-13,-1\)
3. \(m=-3 \pm 10 i\)
5. \(v=7 \pm 3 \sqrt{2}\)
7. \(m=-9,-1\)
9. \(a=\frac{3}{2} \pm \frac{\sqrt{41}}{2}\)
11. \(u=-6 \pm 2 \sqrt{2}\)
Resuelve Ecuaciones Cuadráticas de la Forma \(ax^{2}+bx+c=0\) Completando el Cuadrado
En los siguientes ejercicios, resuelve completando la plaza.
- \(3 p^{2}-18 p+15=15\)
- \(5 q^{2}+70 q+20=0\)
- \(4 y^{2}-6 y=4\)
- \(2 x^{2}+2 x=4\)
- \(3 c^{2}+2 c=9\)
- \(4 d^{2}-2 d=8\)
- \(2 x^{2}+6 x=-5\)
- \(2 x^{2}+4 x=-5\)
- Contestar
-
1. \(p=0,6\)
3. \(y=-\frac{1}{2}, 2\)
5. \(c=-\frac{1}{3} \pm \frac{2 \sqrt{7}}{3}\)
7. \(x=\frac{3}{2} \pm \frac{1}{2} i\)
En los siguientes ejercicios, resuelve mediante el uso de la Fórmula Cuadrática.
- \(4 x^{2}-5 x+1=0\)
- \(7 y^{2}+4 y-3=0\)
- \(r^{2}-r-42=0\)
- \(t^{2}+13 t+22=0\)
- \(4 v^{2}+v-5=0\)
- \(2 w^{2}+9 w+2=0\)
- \(3 m^{2}+8 m+2=0\)
- \(5 n^{2}+2 n-1=0\)
- \(6 a^{2}-5 a+2=0\)
- \(4 b^{2}-b+8=0\)
- \(u(u-10)+3=0\)
- \(5 z(z-2)=3\)
- \(\frac{1}{8} p^{2}-\frac{1}{5} p=-\frac{1}{20}\)
- \(\frac{2}{5} q^{2}+\frac{3}{10} q=\frac{1}{10}\)
- \(4 c^{2}+4 c+1=0\)
- \(9 d^{2}-12 d=-4\)
- Contestar
-
1. \(x=\frac{1}{4}, 1\)
3. \(r=-6,7\)
5. \(v=\frac{-1 \pm \sqrt{21}}{8}\)
7. \(m=\frac{-4 \pm \sqrt{10}}{3}\)
9. \(a=\frac{5}{12} \pm \frac{\sqrt{23}}{12} i\)
11. \(u=5 \pm \sqrt{21}\)
13. \(p=\frac{4 \pm \sqrt{5}}{5}\)
15. \(c=-\frac{1}{2}\)
En los siguientes ejercicios, determine el número de soluciones para cada ecuación cuadrática.
-
- \(9 x^{2}-6 x+1=0\)
- \(3 y^{2}-8 y+1=0\)
- \(7 m^{2}+12 m+4=0\)
- \(5 n^{2}-n+1=0\)
-
- \(5 x^{2}-7 x-8=0\)
- \(7 x^{2}-10 x+5=0\)
- \(25 x^{2}-90 x+81=0\)
- \(15 x^{2}-8 x+4=0\)
- Contestar
-
1.
- \(1\)
- \(2\)
- \(2\)
- \(2\)
En los siguientes ejercicios, identifique el método más apropiado (Factoring, Raíz cuadrada o Fórmula cuadrática) a utilizar para resolver cada ecuación cuadrática. No resuelva.
-
- \(16 r^{2}-8 r+1=0\)
- \(5 t^{2}-8 t+3=9\)
- \(3(c+2)^{2}=15\)
-
- \(4 d^{2}+10 d-5=21\)
- \(25 x^{2}-60 x+36=0\)
- \(6(5 v-7)^{2}=150\)
- Contestar
-
1.
- Factor
- Fórmula cuadrática
- Raíz Cuadrada
Resolver ecuaciones en forma cuadrática
En los siguientes ejercicios, resuelve.
- \(x^{4}-14 x^{2}+24=0\)
- \(x^{4}+4 x^{2}-32=0\)
- \(4 x^{4}-5 x^{2}+1=0\)
- \((2 y+3)^{2}+3(2 y+3)-28=0\)
- \(x+3 \sqrt{x}-28=0\)
- \(6 x+5 \sqrt{x}-6=0\)
- \(x^{\frac{2}{3}}-10 x^{\frac{1}{3}}+24=0\)
- \(x+7 x^{\frac{1}{2}}+6=0\)
- \(8 x^{-2}-2 x^{-1}-3=0\)
- Contestar
-
1. \(x=\pm \sqrt{2}, x=\pm 2 \sqrt{3}\)
3. \(x=\pm 1, x=\pm \frac{1}{2}\)
5. \(x=16\)
7. \(x=64, x=216\)
9. \(x=-2, x=\frac{4}{3}\)
Resolver aplicaciones de ecuaciones cuadráticas
En los siguientes ejercicios, resuelva utilizando el método de factoring, el principio de raíz cuadrada, o la fórmula cuadrática. Redondee sus respuestas a la décima más cercana, si es necesario.
- Encuentra dos números impares consecutivos cuyo producto es \(323\).
- Encuentra dos números pares consecutivos cuyo producto sea \(624\).
- Una pancarta triangular tiene un área de centímetros \(351\) cuadrados. La longitud de la base es dos centímetros más larga que cuatro veces la altura. Encuentra la altura y longitud de la base.
- Julius construyó una vitrina triangular para su colección de monedas. La altura de la vitrina es de seis pulgadas menos del doble del ancho de la base. El área del de la parte posterior de la caja es de pulgadas \(70\) cuadradas. Encuentra la altura y el ancho de la caja.
- Un mosaico de azulejos en forma de triángulo recto se utiliza como la esquina de una vía rectangular. La hipotenusa del mosaico son \(5\) los pies. Un lado del mosaico es el doble de largo que el otro lado. ¿Cuáles son las longitudes de los lados? Redondear a la décima más cercana.
Figura 9.E.1
6. Una pieza rectangular de madera contrachapada tiene una diagonal que mide dos pies más que el ancho. La longitud de la madera contrachapada es el doble del ancho. ¿Cuál es la longitud de la diagonal de la madera contrachapada? Redondear a la décima más cercana.
7. El paseo frontal desde la calle hasta la casa de Pam tiene una superficie de pies \(250\) cuadrados. Su longitud es dos menos de cuatro veces su ancho. Encuentra el largo y ancho de la acera. Redondear a la décima más cercana.
8. Para la fiesta de graduación de Sophia, se dispondrán varias mesas del mismo ancho de extremo a extremo para dar mesa de servir con un área total de pies \(75\) cuadrados. El largo total de las mesas será dos más de tres veces el ancho. Encuentra el largo y ancho de la mesa para servir para que Sophia pueda comprar el mantel de tamaño correcto. Redondear la respuesta a la décima más cercana.
9. Se lanza una pelota verticalmente en el aire con una velocidad de \(160\) pies/seg. Usa la fórmula \(h=-16 t^{2}+v_{0} t\) para determinar cuándo la pelota estará a \(384\) pies del suelo. Redondear a la décima más cercana.
10. La pareja tomó un pequeño avión para un rápido vuelo hasta el país vinícola para una cena romántica y luego regresó a casa. El avión voló un total de \(5\) horas y cada trayecto el viaje fue de \(360\) kilómetros. Si el avión volaba a \(150\) mph, ¿cuál fue la velocidad del viento que afectó al avión?
11. Ezra subió en kayak por el río y luego regresó en un tiempo total de \(6\) horas. El viaje fue \(4\) kilómetros por trayecto y la corriente era difícil. Si Roy kayak a una velocidad de \(5\) mph, ¿cuál fue la velocidad de la corriente?
12. Dos manitas pueden hacer una reparación domiciliaria en \(2\) horas si trabajan juntos. Uno de los hombres toma \(3\) horas más que el otro hombre para terminar el trabajo por sí mismo. ¿Cuánto tiempo tarda cada manitas en hacer la reparación del hogar individualmente?
- Contestar
-
2. Dos números pares consecutivos cuyo producto \(624\) es \(24\) y \(26\), y \(−24\) y \(−26\).
4. El alto es \(14\) pulgadas y el ancho es \(10\) pulgadas.
6. La longitud de la diagonal es de \(3.6\) pies.
8. El ancho de la mesa de servir es de \(4.7\) pies y el largo es de \(16.1\) pies.
Figura 9.E.2 10. La velocidad del viento fue de \(30\) mph.
12. Un hombre tarda \(3\) horas y al otro hombre \(6\) horas para terminar la reparación solo.
Graficar funciones cuadráticas usando propiedades
En los siguientes ejercicios, grafica por punto de trazado.
- Gráfica \(y=x^{2}-2\)
- Gráfica \(y=-x^{2}+3\)
- Contestar
-
2.
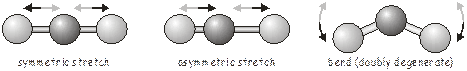
Figura 9.E.3
En los siguientes ejercicios, determine si las siguientes parábolas se abren hacia arriba o hacia abajo.
-
- \(y=-3 x^{2}+3 x-1\)
- \(y=5 x^{2}+6 x+3\)
-
- \(y=x^{2}+8 x-1\)
- \(y=-4 x^{2}-7 x+1\)
- Contestar
-
2.
- Up
- Down
En los siguientes ejercicios, encuentra
- La ecuación del eje de simetría
- El vértice
- \(y=-x^{2}+6 x+8\)
- \(y=2 x^{2}-8 x+1\)
- Contestar
-
2. \(x=2\) ; \((2,-7)\)
En los siguientes ejercicios, encuentra los \(x\)- y \(y\)-interceptos.
- \(y=x^{2}-4x+5\)
- \(y=x^{2}-8x+15\)
- \(y=x^{2}-4x+10\)
- \(y=-5x^{2}-30x-46\)
- \(y=16x^{2}-8x+1\)
- \(y=x^{2}+16x+64\)
- Contestar
-
2. \(\begin{array}{l}{y :(0,15)} \\ {x :(3,0),(5,0)}\end{array}\)
4. \(\begin{array}{l}{y :(0,-46)} \\ {x : \text { none }}\end{array}\)
6. \(\begin{array}{l}{y :(0,-64)} \\ {x :(-8,0)}\end{array}\)
Graficar funciones cuadráticas usando propiedades
En los siguientes ejercicios, grafica mediante el uso de sus propiedades.
- \(y=x^{2}+8 x+15\)
- \(y=x^{2}-2 x-3\)
- \(y=-x^{2}+8 x-16\)
- \(y=4 x^{2}-4 x+1\)
- \(y=x^{2}+6 x+13\)
- \(y=-2 x^{2}-8 x-12\)
- Contestar
-
2.
Figura 9.E.4 4.
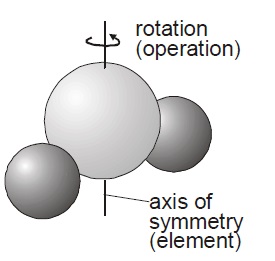
Figura 9.E.5 6.
Figura 9.E.6
En los siguientes ejercicios, encuentra el valor mínimo o máximo.
- \(y=7 x^{2}+14 x+6\)
- \(y=-3 x^{2}+12 x-10\)
- Contestar
-
2. El valor máximo es \(2\) cuando \(x=2\).
En los siguientes ejercicios, resuelve. Redondeo responde a la décima más cercana.
- Se lanza una bola hacia arriba desde el suelo con una velocidad inicial de \(112\) pies/seg. Usa la ecuación cuadrática \(h=-16 t^{2}+112 t\) para encontrar cuánto tiempo tardará la pelota en alcanzar la altura máxima, y luego encontrar la altura máxima.
- Una guardería encierra un área rectangular a lo largo del lado de su edificio para que los niños jueguen al aire libre. Necesitan maximizar el área usando \(180\) pies de esgrima en tres lados del patio. La ecuación cuadrática \(A=-2 x^{2}+180 x\) da el área \(A\),, del patio para la longitud, \(x\), del edificio que bordeará el patio. Encuentra la longitud del edificio que debe bordear el patio para maximizar el área, y luego encontrar el área máxima.
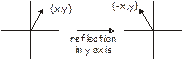
- Contestar
-
2. La longitud adyacente al edificio es de \(90\) pies dando un área máxima de pies \(4,050\) cuadrados.
Graficar funciones cuadráticas usando transformaciones
En los siguientes ejercicios, grafica cada función usando un desplazamiento vertical.
- \(g(x)=x^{2}+4\)
- \(h(x)=x^{2}-3\)
- Contestar
-
2.
Figura 9.E.8
En los siguientes ejercicios, grafica cada función usando un desplazamiento horizontal.
- \(f(x)=(x+1)^{2}\)
- \(g(x)=(x-3)^{2}\)
- Contestar
-
2.
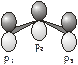
Figura 9.E.9
En los siguientes ejercicios, grafica cada función utilizando transformaciones.
- \(f(x)=(x+2)^{2}+3\)
- \(f(x)=(x+3)^{2}-2\)
- \(f(x)=(x-1)^{2}+4\)
- \(f(x)=(x-4)^{2}-3\)
- Contestar
-
2.
Figura 9.E.10 4.
Figura 9.E.11
En los siguientes ejercicios, grafica cada función.
- \(f(x)=2x^{2}\)
- \(f(x)=-x^{2}\)
- \(f(x)=\frac{1}{2} x^{2}\)
- Contestar
-
2.
Figura 9.E.12
En los siguientes ejercicios, reescribe cada función en el \(f(x)=a(x-h)^{2}+k\) formulario completando el cuadrado.
- \(f(x)=2 x^{2}-4 x-4\)
- \(f(x)=3 x^{2}+12 x+8\)
- Contestar
-
1. \(f(x)=2(x-1)^{2}-6\)
En los siguientes ejercicios,
- Reescribe cada función en \(f(x)=a(x−h)^{2}+k\) forma
- Gráficalo mediante transformaciones
- \(f(x)=3 x^{2}-6 x-1\)
- \(f(x)=-2 x^{2}-12 x-5\)
- \(f(x)=2 x^{2}+4 x+6\)
- \(f(x)=3 x^{2}-12 x+7\)
- Contestar
-
1.
- \(f(x)=3(x-1)^{2}-4\)
Figura 9.E.13
3.
- \(f(x)=2(x+1)^{2}+4\)
Figura 9.E.14
En los siguientes ejercicios,
- Reescribe cada función en \(f(x)=a(x−h)^{2}+k\) forma
- Gráfiquela usando propiedades
- \(f(x)=-3 x^{2}-12 x-5\)
- \(f(x)=2 x^{2}-12 x+7\)
- Contestar
-
1.
- \(f(x)=-3(x+2)^{2}+7\)
Figura 9.E.15
En los siguientes ejercicios, escribe la función cuadrática en \(f(x)=a(x−h)^{2}+k\) forma.
Figura 9.E.16
Figura 9.E.17
- Contestar
-
1. \(f(x)=(x+1)^{2}-5\)
Resolver desigualdades cuadráticas
En los siguientes ejercicios, resuelve gráficamente y escribe la solución en notación de intervalos.
- \(x^{2}-x-6>0\)
- \(x^{2}+4 x+3 \leq 0\)
- \(-x^{2}-x+2 \geq 0\)
- \(-x^{2}+2 x+3<0\)
- Contestar
-
1.
Figura 9.E.18- \((-\infty,-2) \cup(3, \infty)\)
3.
Figura 9.E.19- \([-2,1]\)
En los siguientes ejercicios, resuelve cada desigualdad algebraicamente y escribe cualquier solución en notación de intervalos.
- \(x^{2}-6 x+8<0\)
- \(x^{2}+x>12\)
- \(x^{2}-6 x+4 \leq 0\)
- \(2 x^{2}+7 x-4>0\)
- \(-x^{2}+x-6>0\)
- \(x^{2}-2 x+4 \geq 0\)
- Contestar
-
1. \((2,4)\)
3. \([3-\sqrt{5}, 3+\sqrt{5}]\)
5. ninguna solución
Prueba de práctica
- Utilice la Propiedad Raíz Cuadrada para resolver la ecuación cuadrática \(3(w+5)^{2}=27\).
- Use Completar el Cuadrado para resolver la ecuación cuadrática \(a^{2}-8 a+7=23\).
- Utilice la fórmula cuadrática para resolver la ecuación cuadrática \(2 m^{2}-5 m+3=0\).
- Contestar
-
1. \(w=-2, w=-8\)
3. \(m=1, m=\frac{3}{2}\)
Resuelve las siguientes ecuaciones cuadráticas. Utilice cualquier método.
- \(2 x(3 x-2)-1=0\)
- \(\frac{9}{4} y^{2}-3 y+1=0\)
- Contestar
-
2. \(y=\frac{2}{3}\)
Utilice el discriminante para determinar el número y tipo de soluciones de cada ecuación cuadrática.
- \(6 p^{2}-13 p+7=0\)
- \(3 q^{2}-10 q+12=0\)
- Contestar
-
2. \(2\) complejo
Resuelve cada ecuación.
- \(4 x^{4}-17 x^{2}+4=0\)
- \(y^{\frac{2}{3}}+2 y^{\frac{1}{3}}-3=0\)
- Contestar
-
2. \(y=1, y=-27\)
Para cada parábola, encuentra
- En qué dirección se abre
- La ecuación del eje de simetría
- El vértice
- El \(x\)-y \(y\)-intercepta
- El valor máximo o mínimo
- \(y=3 x^{2}+6 x+8\)
- \(y=-x^{2}-8 x+16\)
- Contestar
-
2.
- abajo
- \(x=-4\)
- \((-4,0)\)
- \(y: (0,16); x: (-4,0)\)
- valor mínimo de \(-4\) cuando \(x=0\)
Gráfica cada función cuadrática usando interceptos, el vértice y la ecuación del eje de simetría.
- \(f(x)=x^{2}+6 x+9\)
- \(f(x)=-2 x^{2}+8 x+4\)
- Contestar
-
2.
Figura 9.E.20
En los siguientes ejercicios, grafica cada función utilizando transformaciones.
- \(f(x)=(x+3)^{2}+2\)
- \(f(x)=x^{2}-4 x-1\)
- Contestar
-
2.
Figura 9.E.21
En los siguientes ejercicios, resuelve cada desigualdad algebraicamente y escribe cualquier solución en notación de intervalos.
- \(x^{2}-6 x-8 \leq 0\)
- \(2 x^{2}+x-10>0\)
- Contestar
-
2. \(\left(-\infty,-\frac{5}{2}\right) \cup(2, \infty)\)
Modele la situación con una ecuación cuadrática y resuelva por cualquier método.
- Encuentra dos números pares consecutivos cuyo producto sea \(360\).
- La longitud de una diagonal de un rectángulo es tres más que la anchura. La longitud del rectángulo es tres veces la anchura. Encuentra la longitud de la diagonal. (Redondee a la décima más cercana.)
- Contestar
-
2. Se lanza un globo de agua hacia arriba a una velocidad de \(86\) pies/seg. Usando la fórmula \(h=-16 t^{2}+86 t\) encuentra cuánto tiempo tardará el globo en alcanzar la altura máxima, y luego encuentra la altura máxima. Redondear a la décima más cercana.