2.1: Ley de Pascal
- Page ID
- 153140
Describir la Ley de Pascal y la fórmula utilizada para relacionar fuerza, presión y área. Resolver para F en términos de p y A. Resolver para p en términos de F y A. Resolver para A en términos de F y p.
Enumere las unidades comunes de fuerza, presión y área.
Determinar la equivalencia para psi, Pa y barra.
Si el área se mantiene constante, determine cómo los cambios en la presión afectan a la fuerza.
Si la presión se mantiene constante, determine cómo los cambios en el área afectan a la fuerza.
Si el área se mantiene constante, determine cómo los cambios en la fuerza afectan la presión.
Si la fuerza se mantiene constante, determine cómo los cambios en el área afectan la presión.
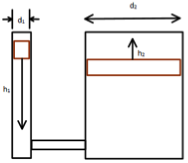 Dado un sistema de multiplicación de fuerza con las siguientes dimensiones:
Dado un sistema de multiplicación de fuerza con las siguientes dimensiones:
d 1 = 3/4 in
F 1 = 120 lbf
h 1 = 4 in
d 2 = 1 ¼ in
Calcular A 1, p, V 1, A 2, F 2, h 2, energía adentro, energía afuera
Comente las diferencias entre el extremo de la tapa y el extremo de la varilla de un cilindro de doble efecto con respecto al área funcional.
Explique por qué la presión necesaria para retraer es mayor que la presión necesaria para extenderse con la misma fuerza para un cilindro de doble efecto.
Explique por qué la fuerza de extensión es mayor que la fuerza de retracción dado el mismo límite de presión para un cilindro de doble efecto.
Dado el cilindro X con las siguientes dimensiones:
d cap = 2 7/8 in
d varilla = 7/8 in
Calcular p ext y p ret para el cilindro X dado que el sistema tiene la tarea de mover un objeto de 1350lbf.
Calcule F ExtMax y F RetMax para el cilindro X dado que el sistema está limitado a 640 psi.



