3.1: Señales Digitales y Puertas
- Page ID
- 154412
Si bien el sistema de numeración binaria es una abstracción matemática interesante, aún no hemos visto su aplicación práctica a la electrónica. Este capítulo está dedicado precisamente a eso: prácticamente aplicar el concepto de bits binarios a los circuitos. Lo que hace que la numeración binaria sea tan importante para la aplicación de la electrónica digital es la facilidad en la que los bits pueden ser representados en términos físicos. Debido a que un bit binario solo puede tener uno de dos valores diferentes, ya sea 0 o 1, cualquier medio físico capaz de conmutar entre dos estados saturados puede usarse para representar un bit. En consecuencia, cualquier sistema físico capaz de representar bits binarios es capaz de representar cantidades numéricas y potencialmente tiene la capacidad de manipular esos números. Este es el concepto básico que subyace a la computación digital.
Los circuitos electrónicos son sistemas físicos que se prestan bien a la representación de números binarios. Los transistores, cuando funcionan en sus límites de polarización, pueden estar en uno de dos estados diferentes: ya sea de corte (sin corriente controlada) o de saturación (corriente máxima controlada). Si un circuito transistor está diseñado para maximizar la probabilidad de caer en cualquiera de estos estados (y no operar en el modo lineal, o activo), puede servir como una representación física de un bit binario. Una señal de voltaje medida en la salida de dicho circuito también puede servir como una representación de un solo bit, un voltaje bajo que representa un “0” binario y un voltaje (relativamente) alto que representa un “1” binario. Tenga en cuenta el siguiente circuito de transistores:
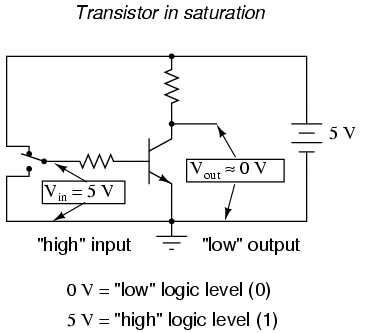
En este circuito, el transistor se encuentra en un estado de saturación en virtud de la tensión de entrada aplicada (5 voltios) a través del interruptor de dos posiciones. Debido a que está saturado, el transistor baja muy poco voltaje entre colector y emisor, resultando en un voltaje de salida de (prácticamente) 0 voltios. Si estuviéramos usando este circuito para representar bits binarios, diríamos que la señal de entrada es un “1” binario y que la señal de salida es un “0” binario. Cualquier voltaje cercano al voltaje de suministro completo (medido en referencia a tierra, por supuesto) se considera un “1” y la falta de voltaje se considera un “0”. Los términos alternativos para estos niveles de voltaje son altos (lo mismo que un “1” binario) y bajo (lo mismo que un “0” binario). Un término general para la representación de un bit binario por una tensión de circuito es el nivel lógico.
Al mover el switch a la otra posición, aplicamos un binario “0” a la entrada y recibimos un binario “1” en la salida:
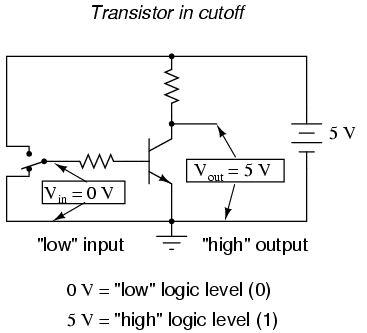
Lo que hemos creado aquí con un solo transistor es un circuito generalmente conocido como puerta lógica, o simplemente puerta. Una puerta es un tipo especial de circuito amplificador diseñado para aceptar y generar señales de voltaje correspondientes a 1 y 0 binarios. Como tal, las puertas no están destinadas a ser utilizadas para amplificar señales analógicas (señales de voltaje entre 0 y voltaje completo). Utilizadas juntas, se pueden aplicar múltiples puertas a la tarea de almacenamiento de números binarios (circuitos de memoria) o manipulación (circuitos de computación), representando la salida de cada puerta un bit de un número binario de varios bits. Apenas cómo se hace esto es un tema para un capítulo posterior. En este momento es importante enfocarse en el funcionamiento de portones individuales.
La puerta que se muestra aquí con el transistor único se conoce como un inversor, o NO puerta porque emite la señal digital exactamente opuesta como lo que es entrada. Por conveniencia, los circuitos de puerta generalmente están representados por sus propios símbolos en lugar de por sus transistores y resistencias constituyentes. El siguiente es el símbolo para un inversor:
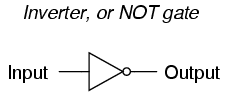
Aquí se muestra un símbolo alternativo para un inversor:
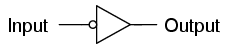
Observe la forma triangular del símbolo de puerta, muy parecida a la de un amplificador operacional. Como se dijo antes, los circuitos de puerta en realidad son amplificadores. El círculo pequeño o “burbuja” que se muestra en el terminal de entrada o salida es estándar para representar la función de inversión. Como podría sospechar, si tuviéramos que quitar la burbuja del símbolo de puerta, dejando solo un triángulo, el símbolo resultante ya no indicaría inversión, sino meramente amplificación directa. Tal símbolo y tal puerta realmente existen, y se llama búfer, el tema de la siguiente sección.
Al igual que un símbolo de amplificador operacional, las conexiones de entrada y salida se muestran como cables simples, siendo el punto de referencia implícito para cada señal de voltaje “tierra”. En los circuitos de puerta digital, la tierra es casi siempre la conexión negativa de una sola fuente de voltaje (fuente de alimentación). Las fuentes de alimentación dobles o “divididas” rara vez se utilizan en circuitos de puerta. Debido a que los circuitos de puerta son amplificadores, requieren una fuente de energía para operar. Al igual que los amplificadores operativos, las conexiones de suministro de energía para puertas digitales a menudo se omiten del símbolo por simplicidad. Si tuviéramos que mostrar todas las conexiones necesarias para operar esta puerta, el esquema se vería así:
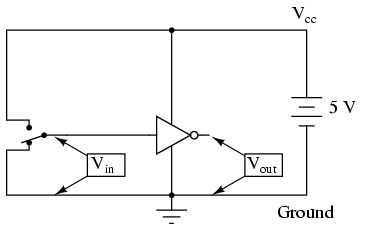
Los conductores de la fuente de alimentación rara vez se muestran en los esquemas del circuito de puerta, incluso si las conexiones de la fuente de alimentación en cada puerta son Minimizando líneas en nuestro esquema, obtenemos esto:
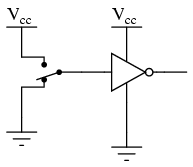
“V cc” significa el voltaje constante suministrado al colector de un circuito de transistor de unión bipolar, en referencia a tierra. Esos puntos en un circuito de puerta marcados por la etiqueta “V cc” están todos conectados al mismo punto, y ese punto es el terminal positivo de una fuente de voltaje de CC, generalmente de 5 voltios.
Como veremos en otras secciones de este capítulo, existen bastantes tipos diferentes de puertas lógicas, la mayoría de las cuales tienen múltiples terminales de entrada para aceptar más de una señal. La salida de cualquier puerta depende del estado de su (s) entrada (s) y su función lógica.
Expresar funciones de circuito de puerta con tablas de verdad
Una forma común de expresar la función particular de un circuito de puerta se llama tabla de verdad. Las tablas de verdad muestran todas las combinaciones de condiciones de entrada en términos de estados de nivel lógico (ya sea “alto” o “bajo”, “1” o “0” para cada terminal de entrada de la puerta), junto con el nivel lógico de salida correspondiente, ya sea “alto” o “bajo”. Para el circuito inversor, o NO, que acaba de ilustrarse, la tabla de la verdad es muy simple de hecho:
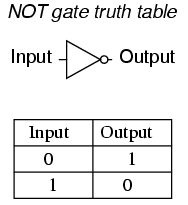
Las mesas de verdad para puertas más complejas son, por supuesto, más grandes que la que se muestra para la puerta NOT. La tabla de verdad de una puerta debe tener tantas filas como posibilidades para combinaciones de entrada únicas. Para una puerta de entrada única como la puerta NOT, solo hay dos posibilidades, 0 y 1. Para una puerta de dos entradas, hay cuatro posibilidades (00, 01, 10 y 11), y así cuatro filas a la tabla de verdad correspondiente. Para una puerta de tres entradas, hay ocho posibilidades (000, 001, 010, 011, 100, 101, 110 y 111), y así se necesita una tabla de verdad con ocho filas. El matemáticamente inclinado se dará cuenta de que el número de filas de la tabla de verdad necesarias para una puerta es igual a 2 elevado a la potencia del número de terminales de entrada.
Revisar
- En los circuitos digitales, los valores binarios de bit de 0 y 1 están representados por señales de voltaje medidas en referencia a un punto de circuito común llamado tierra. La ausencia de voltaje representa un “0” binario y la presencia de voltaje de suministro completo de CC representa un “1” binario.
- Una puerta lógica, o simplemente puerta, es una forma especial de circuito amplificador diseñado para la entrada y salida de voltajes de nivel lógico (voltajes destinados a representar bits binarios). Los circuitos de puerta se representan más comúnmente en un esquema por sus propios símbolos únicos en lugar de por sus transistores y resistencias constituyentes.
- Al igual que con los amplificadores operativos, las conexiones de la fuente de alimentación a las puertas a menudo se omiten en diagramas esquemáticos en aras de la simplicidad.
- Una tabla de verdad es una forma estándar de representar las relaciones de entrada/salida de un circuito de puerta, enumerando todas las posibles combinaciones de niveles lógicos de entrada con sus respectivos niveles lógicos de salida.


