11.1: Secuencia de Recuento Binario

Última actualización
Guardar como PDF

Page ID: 154416

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

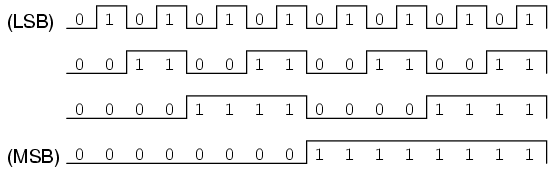
Si examinamos una secuencia de conteo binario de cuatro bits de 0000 a 1111, un patrón definido será evidente en las “oscilaciones” de los bits entre 0 y 1:

Observe cómo el bit menos significativo (LSB) conmuta entre 0 y 1 para cada paso en la secuencia de conteo, mientras que cada bit siguiente conmuta a la mitad de la frecuencia del anterior. El bit más significativo (MSB) solo conmuta una vez durante toda la secuencia de conteo de dieciséis pasos: en la transición entre 7 (0111) y 8 (1000).

Si quisiéramos diseñar un circuito digital para “contar” en binario de cuatro bits, todo lo que tendríamos que hacer es diseñar una serie de circuitos divisores de frecuencia, dividiendo cada circuito la frecuencia de un pulso de onda cuadrada por un factor de 2:

Los biestables J-K son ideales para esta tarea, ya que tienen la capacidad de “alternar” su estado de salida al comando de un pulso de reloj cuando las entradas J y K se hacen “altas” (1):

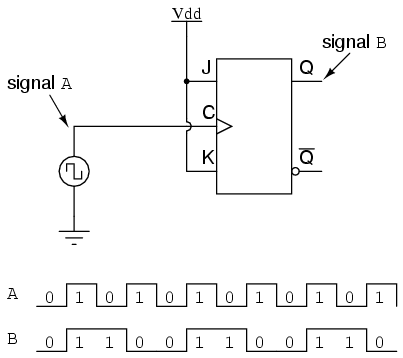
Si consideramos que las dos señales (A y B) en este circuito representan dos bits de un número binario, siendo la señal A el LSB y siendo la señal B el MSB, vemos que la secuencia de conteo es hacia atrás: de 11 a 10 a 01 a 00 y de nuevo a 11. Aunque podría no estar contando en la dirección que podríamos haber asumido, ¡al menos cuenta!

Las siguientes secciones exploran diferentes tipos de circuitos de contador, todos hechos con flip-flops J-K, y todos basados en la explotación del modo de operación toggle de ese flip-flop.

Revisar

Las secuencias de conteo binario siguen un patrón de división de frecuencia de octava: la frecuencia de oscilación para cada bit, de LSB a MSB, sigue un patrón de división por dos. En otras palabras, el LSB oscilará a la frecuencia más alta, seguido del siguiente bit a la mitad de la frecuencia del LSB, y el siguiente bit a la mitad de la frecuencia del bit anterior, etc.
Se pueden construir circuitos que “cuenten” en una secuencia binaria, usando flip-flops J-K establecidos en el modo “toggle”.