4.6: Logaritmos
- Page ID
- 153841
Definición de un logaritmo
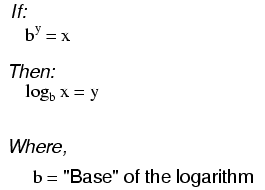
“log” denota un logaritmo común (base = 10), mientras que “ln” denota un logaritmo natural (base = e).
Propiedades de logaritmos
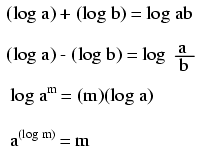
Estas propiedades de logaritmos son útiles para realizar operaciones complejas de multiplicación y división. Son un ejemplo de algo llamado función de transformación, por lo que un tipo de operación matemática se transforma en otro tipo de operación matemática que es más simple de resolver. Usando una tabla de cifras logarítmicas, se pueden multiplicar o dividir números sumando o restando sus logaritmos, respectivamente. luego buscar esa cifra logaritmo en la tabla y ver cuál es el producto final o cociente.
Las reglas de cálculo funcionan sobre este principio de logaritmos realizando multiplicación y división a través de la suma y resta de distancias en la diapositiva.
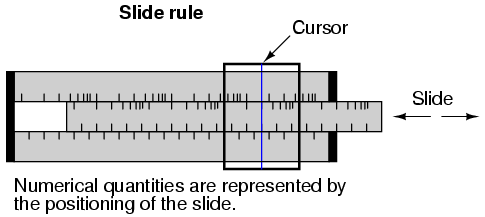
Las marcas en las escalas de una regla de cálculo están espaciadas de manera logarítmica, de modo que un posicionamiento lineal de la escala o cursor da como resultado una indicación no lineal como se lee en la (s) escala (s). Sumar o restar longitudes en estas escalas logarítmicas da como resultado una indicación equivalente al producto o cociente, respectivamente, de esas longitudes.
La mayoría de las reglas de cálculo también estaban equipadas con escalas especiales para funciones trigonométricas, potencias, raíces y otras funciones aritméticas útiles.


