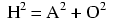5.1: Trigonometría de Triángulo Recto
- Page ID
- 154106
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
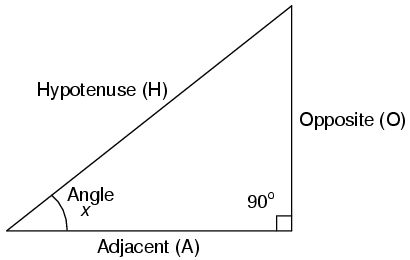
Un triángulo rectángulo se define como tener un ángulo exactamente igual a 90 o (un ángulo recto).
Identidades trigonométricas

H es la Hipotenusa, siendo siempre opuesta al ángulo recto. Relativo al ángulo x, O es el Opuesto y A es el Adyacente.
Las funciones “arco” como “arcsin”, “arccos” y “arctan” son los complementos de las funciones trigonométricas normales. Estas funciones devuelven un ángulo para una entrada de relación. Por ejemplo, si la tangente de 45 o es igual a 1, entonces el “arcotangente” (arctan) de 1 es 45 o. Las funciones “Arco” son útiles para encontrar ángulos en un triángulo rectángulo si se conocen las longitudes de los lados.
El teorema de Pitágoras