6.4: Derivadas de Funciones de Potencia de e

Última actualización
Guardar como PDF

Page ID: 154016

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ejemplo Derivadas de e

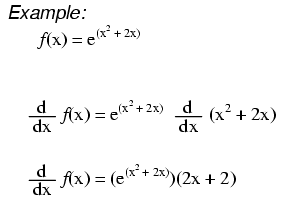
Constante de proporcionalidad

Cuando decimos que una relación o fenómeno es “exponencial”, estamos dando a entender que cierta cantidad —corriente eléctrica, ganancias, población— aumenta más rápidamente a medida que crece la cantidad. En otras palabras, la tasa de cambio con respecto a una variable dada es proporcional al valor de esa variable. Esto significa que la derivada de una función exponencial es igual a la función exponencial original multiplicada por una constante (k) que establece proporcionalidad.

La constante de proporcionalidad es igual al logaritmo natural de la base del exponente:

Se deduce, entonces, que si el logaritmo natural de la base es igual a uno, la derivada de la función será igual a la función original. Esto es exactamente lo que sucede con las funciones de potencia de e: el logaritmo natural de e es 1, y consecuentemente, la derivada de e ^x es e ^x.

La regla de la “cadena”

Cuando la expresión exponencial es algo distinto a simplemente x, aplicamos la regla de la cadena: Primero tomamos la derivada de toda la expresión, luego la multiplicamos por la derivada de la expresión en el exponente.

Esta técnica se puede utilizar para encontrar la tasa de cambio de la corriente del diodo con respecto al voltaje del diodo.

La siguiente ecuación proporciona una relación aproximada entre el voltaje a través de un diodo ($V_D$) y la corriente a través de un diodo ($I_D$):

(Consulte la página sobre diodos y rectificadores para obtener más información sobre la ecuación de corriente-voltaje de diodo; también, tenga en cuenta que ($I_S$) es una constante, no una variable). Para encontrar la tasa de cambio de corriente con respecto al voltaje, tomamos la derivada:

Por lo tanto, a un valor dado de voltaje de diodo ($V_D$), un aumento incremental en el voltaje creará un aumento en la corriente igual a $$\ frac {I_S} {0.026} e^\ frac {V_D} {0.026}\]