1.4: Cálculos simples de circuitos de CA
- Page ID
- 153416
En el transcurso de los próximos capítulos, aprenderá que las mediciones y cálculos de circuitos de CA pueden complicarse mucho debido a la naturaleza compleja de la corriente alterna en circuitos con inductancia y capacitancia. Sin embargo, con circuitos simples (figura a continuación) que involucran nada más que una fuente de alimentación de CA y resistencia, las mismas leyes y reglas de CC se aplican de manera simple y directa.
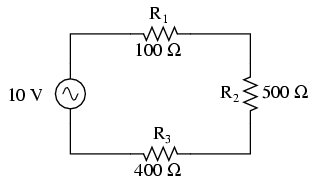
Los cálculos de circuitos de CA para circuitos resistivos son los mismos que para CC.
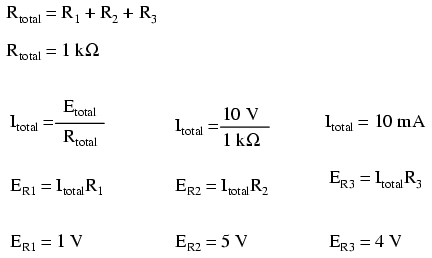
Las resistencias en serie aún se suman, las resistencias paralelas siguen disminuyendo y las Leyes de Kirchhoff y Ohm siguen siendo ciertas. En realidad, como descubriremos más adelante, estas reglas y leyes siempre son ciertas, es solo que tenemos que expresar las cantidades de voltaje, corriente y oposición a la corriente en formas matemáticas más avanzadas. Sin embargo, con circuitos puramente resistivos, estas complejidades de CA no tienen consecuencias prácticas, por lo que podemos tratar los números como si estuviéramos tratando con cantidades simples de CC.
Debido a que todas estas relaciones matemáticas siguen siendo ciertas, podemos hacer uso de nuestro conocido método de “tabla” de organizar los valores del circuito al igual que con DC:
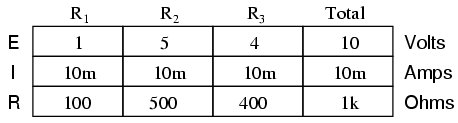
Aquí se debe dar una advertencia importante: todas las mediciones de voltaje y corriente de CA deben expresarse en los mismos términos (pico, pico a pico, promedio o RMS). Si el voltaje de la fuente se da en voltios de CA pico, entonces todas las corrientes y voltajes calculados posteriormente se moldean en términos de unidades de pico. Si el voltaje de la fuente se da en voltios RMS de CA, entonces todas las corrientes y voltajes calculados también se emiten en unidades RMS de CA. Esto es válido para cualquier cálculo basado en las leyes de Ohm, las leyes de Kirchhoff, etc. A menos que se indique lo contrario, todos los valores de voltaje y corriente en los circuitos de CA generalmente se supone que son RMS en lugar de pico, promedio o pico a pico. En algunas áreas de la electrónica, se suponen mediciones de pico, pero en la mayoría de las aplicaciones (especialmente la electrónica industrial) la suposición es RMS.
- REVISIÓN:
Todas las viejas reglas y leyes de CC (Leyes de Voltaje y Corriente de Kirchhoff, Ley de Ohm) siguen siendo válidas para AC. Sin embargo, con circuitos más complejos, es posible que necesitemos representar las cantidades de CA en forma más compleja. Más sobre esto después, ¡lo prometo!
El método de “tabla” para organizar los valores de los circuitos sigue siendo una herramienta de análisis válida para circuitos de CA.


