6.2: Resonancia simple en paralelo (circuito de tanque)
- Page ID
- 153285
Resonancia en un Circuito de Tanques
Se experimentará una condición de resonancia en un circuito de tanque (Figura a continuación) cuando las reactancias del condensador y el inductor sean iguales entre sí. Debido a que la reactancia inductiva aumenta al aumentar la frecuencia y la reactancia capacitiva disminuye al aumentar la frecuencia, solo habrá una frecuencia donde estas dos reactancias serán iguales.
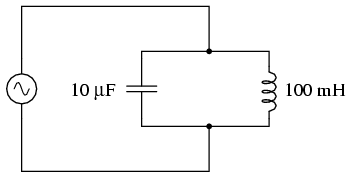
Circuito resonante paralelo simple (circuito de tanque).
En el circuito anterior, tenemos un condensador de 10 µF y un inductor de 100 mH. Como conocemos las ecuaciones para determinar la reactancia de cada una a una frecuencia dada, y estamos buscando ese punto donde las dos reactancias sean iguales entre sí, podemos establecer las dos fórmulas de reactancia iguales entre sí y resolver la frecuencia algebraicamente:

Entonces ahí lo tenemos: una fórmula para decirnos la frecuencia resonante de un circuito tanque, dados los valores de inductancia (L) en Henrys y capacitancia (C) en Faradios. Conectando los valores de L y C en nuestro circuito de ejemplo, llegamos a una frecuencia resonante de 159.155 Hz.
Cálculo de impedancias individuales
Lo que sucede en la resonancia es bastante interesante. Con reactancias capacitivas e inductivas iguales entre sí, la impedancia total aumenta hasta el infinito, lo que significa que el circuito del tanque no extrae corriente de la fuente de alimentación de CA. Podemos calcular las impedancias individuales del condensador de 10 µF y el inductor de 100 mH y trabajar a través de la fórmula de impedancia paralela para demostrar esto matemáticamente:
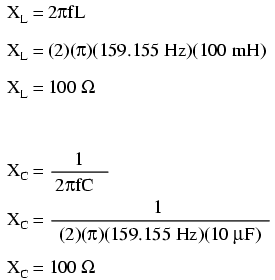
Como habrás adivinado, elegí estos valores de componentes para dar impedancias de resonancia que eran fáciles de trabajar (100 Ω incluso).
Fórmula de impedancia paralela
Ahora, usamos la fórmula de impedancia paralela para ver qué sucede con el total\(Z\):
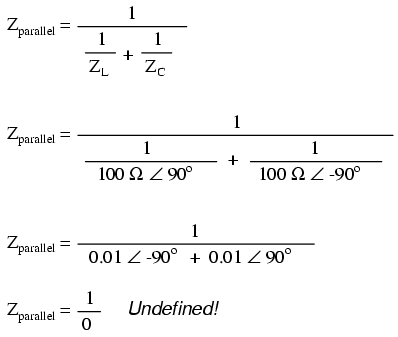
\[ Z_{parallel} = \dfrac{1}{\dfrac{1}{Z_L} + \dfrac{1}{Z_C}}\]
Parcela de simulación SPICE
No podemos dividir ningún número por cero y llegar a un resultado significativo, pero podemos decir que el resultado se acerca a un valor de infinito a medida que las dos impedancias paralelas se acercan entre sí. Lo que esto significa en términos prácticos es que, la impedancia total de un circuito tanque es infinita (comportándose como un circuito abierto) en resonancia. Podemos trazar las consecuencias de esto en un amplio rango de frecuencias de fuente de alimentación con una simulación SPICE corta: (Figura abajo)
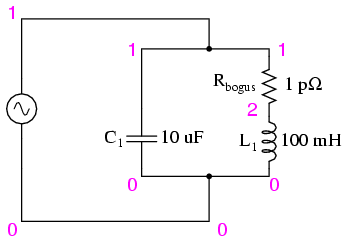
Circuito resonante sutitable para simulación SPICE.
La resistencia de 1 pico-ohmio (1 pΩ) se coloca en este análisis SPICE para superar una limitación de SPICE: es decir, que no puede analizar un circuito que contenga un bucle directo de fuente de inductor-voltaje. (Figura abajo) Se eligió un valor de resistencia muy bajo para tener un efecto mínimo en el comportamiento del circuito.
Esta simulación SPICE traza la corriente del circuito en un rango de frecuencia de 100 a 200 Hz en veinte pasos pares (100 y 200 Hz inclusive). La magnitud actual en la gráfica aumenta de izquierda a derecha, mientras que la frecuencia aumenta de arriba a abajo. La corriente en este circuito toma una fuerte caída alrededor del punto de análisis de 157.9 Hz, que es el punto de análisis más cercano a nuestra frecuencia de resonancia predicha de 159.155 Hz. Es en este punto que la corriente total de la fuente de alimentación cae a cero.
La gráfica del postprocesador gráfico “Nuez moscada”
La gráfica anterior se produce a partir del archivo de circuito de especias anterior (*.cir), el comando (.plot) en la última línea que produce la gráfica de texto en cualquier impresora o terminal. Una trama de mejor aspecto es producida por el postprocesador gráfico “nuez moscada”, parte del paquete de especias. El spice anterior (*.cir) no requiere el comando plot (.plot), aunque no hace daño. Los siguientes comandos producen la siguiente gráfica: (Figura abajo)
Del aviso de nuez moscada:
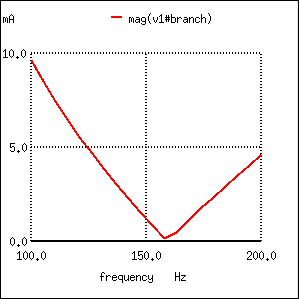
Nuez moscada produce parcela de corriente I (v1) para circuito resonante paralelo.
Parcelas de Bode
Por cierto, la salida gráfica producida por este análisis por computadora SPICE se conoce más generalmente como una gráfica de Bode. Dichas gráficas trazan amplitud o desplazamiento de fase en un eje y frecuencia en el otro. La pendiente de una curva gráfica de Bode caracteriza la “respuesta de frecuencia” de un circuito, o cuán sensible es a los cambios en la frecuencia.
Revisar
- La resonancia ocurre cuando las reactancias capacitivas e inductivas son iguales entre sí.
- Para un circuito de tanque sin resistencia (R), la frecuencia resonante se puede calcular con la siguiente fórmula:
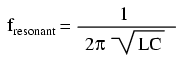
- La impedancia total de un circuito LC paralelo se acerca al infinito cuando la frecuencia de la fuente de alimentación se acerca a la resonancia.
- Una gráfica de Bode es una gráfica que traza la amplitud o fase de la forma de onda en un eje y la frecuencia en el otro.


