6.4: Aplicaciones de Resonancia

Última actualización
Guardar como PDF

Page ID: 153284

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Hasta el momento, el fenómeno de la resonancia parece ser una curiosidad inútil, o a lo sumo una molestia a evitar (¡especialmente si la resonancia en serie produce un cortocircuito en nuestra fuente de voltaje de CA!). Sin embargo, este no es el caso. La resonancia es una propiedad muy valiosa de los circuitos de CA reactivos, empleados en una variedad de aplicaciones.

Un uso para la resonancia es establecer una condición de frecuencia estable en circuitos diseñados para producir señales de CA. Por lo general, se utiliza un circuito paralelo (tanque) para este propósito, con el condensador y el inductor conectados directamente entre sí, intercambiando energía entre sí. Así como un péndulo se puede usar para estabilizar la frecuencia de las oscilaciones de un mecanismo de reloj, también se puede usar un circuito de tanque para estabilizar la frecuencia eléctrica de un circuito oscilador de CA. Como se señaló anteriormente, la frecuencia establecida por el circuito del tanque depende únicamente de los valores de L y C, y no de las magnitudes de voltaje o corriente presentes en las oscilaciones: (Figura a continuación)

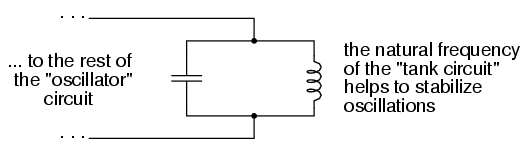
El circuito resonante sirve como fuente de frecuencia estable.

Otro uso para la resonancia es en aplicaciones donde se desean los efectos de una impedancia muy incrementada o disminuida a una frecuencia particular. Un circuito resonante puede ser utilizado para “bloquear” (presente alta impedancia hacia) una frecuencia o rango de frecuencias, actuando así como una especie de “filtro” de frecuencia para forzar ciertas frecuencias fuera de una mezcla de otras. De hecho, estos circuitos particulares se llaman filtros, y su diseño constituye una disciplina de estudio por sí solo: (Figura a continuación)

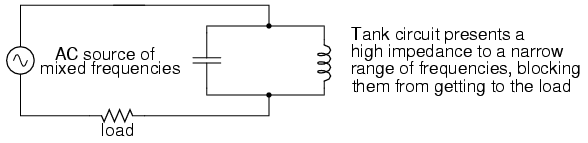
El circuito resonante sirve como filtro.

En esencia, así es como funcionan los circuitos sintonizadores de receptores de radio analógicos para filtrar, o seleccionar, una frecuencia de estación de la mezcla de diferentes señales de frecuencia de estación de radio interceptadas por la antena.

REVISAR

La resonancia se puede emplear para mantener las oscilaciones del circuito de CA a una frecuencia constante, así como un péndulo se puede usar para mantener una velocidad de oscilación constante en un mecanismo de cronometraje.
La resonancia se puede explotar por sus propiedades de impedancia: ya sea aumentando drásticamente o disminuyendo la impedancia para ciertas frecuencias. Los circuitos diseñados para filtrar ciertas frecuencias de una mezcla de diferentes frecuencias se denominan filtros.