1.1: Ángulos

Última actualización
Guardar como PDF

Page ID: 151403

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

¿Cuál es el problema con los ángulos de todos modos?

Antes incluso de entrar en trigonometría, necesitamos discutir los ángulos. No te preocupes. Las cosas no se van a poner demasiado locas. Lo prometo. Repasemos primero lo básico.

Titulación. Trescientos sesenta de la circunferencia de un círculo. También es la unidad por la que medimos los ángulos.

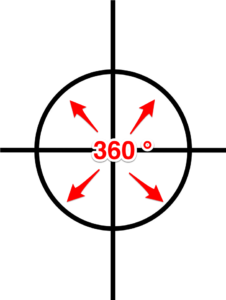
Figura 1. Grados

Ángulo. Este es el espacio entre dos líneas que se cruzan.

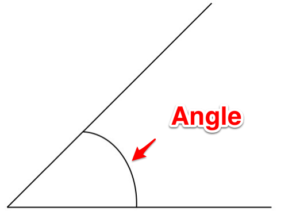
Figura 2. Ángulo

Ángulos complementarios. Se trata de dos ángulos cuya suma equivale a 90 grados.

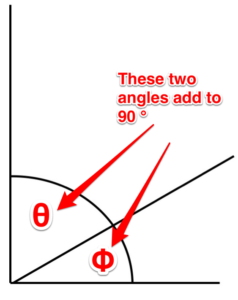
Figura 3. Ángulo complementario

Ángulos suplementarios. Se trata de dos ángulos cuya suma equivale a 180 grados.

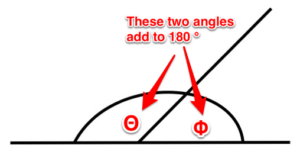
Figura 4. Ángulo suplementario

Ángulo agudo. Un ángulo que es menor a 90 grados.

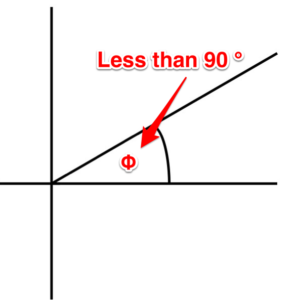
Figura 5. Ángulo agudo

Ángulo obtuso. Un ángulo que es mayor a 90 grados.

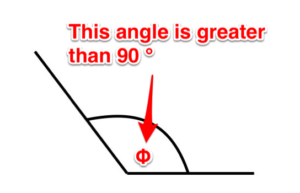
Figura 6. Ángulo obtuso

Ángulos similares. Es posible que los triángulos tengan lados de diferentes tamaños pero compartan los mismos ángulos de tamaño. Estos se llaman ángulos similares.

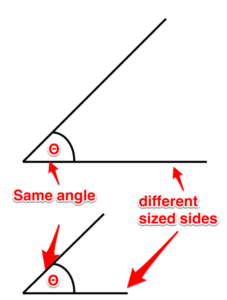
Figura 7. Ángulos similares

Ángulo recto. Este es un ángulo que es de 90 grados.

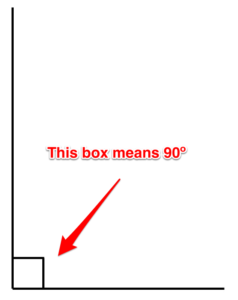
Figura 8. Ángulo recto

Hay un montón de información sobre ángulos en los que no necesitamos meternos. Recuerda: Trata de no complicar demasiado las cosas. Solo concéntrate en lo básico y estarás bien.