1.2: Triángulos

Última actualización
Guardar como PDF

Page ID: 151434

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Por qué los triángulos son importantes

El aprendizaje de la teoría eléctrica requiere el estudio de los triángulos. Más específicamente: triángulos rectos. Antes de cavar demasiado en el triángulo rectángulo, repasemos dos puntos clave sobre los triángulos.

Todos los triángulos tienen tres lados. (Presente este hecho bajo la categoría “Gracias Capitán Obvio”.)
Todos los triángulos contienen 180 grados.

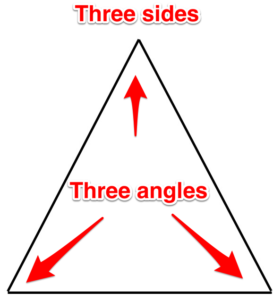
Figura 9. Triángulo

Diferentes triángulos

El triángulo rectángulo es el triángulo más común que se utilizará en la teoría eléctrica. Es una buena idea tener una comprensión básica de otros triángulos también. Aquí hay algunos triángulos comunes con los que te encontrarás en la trigonometría.

Triángulo isósceles. Este triángulo tiene dos lados que son iguales, y dos ángulos que son iguales.

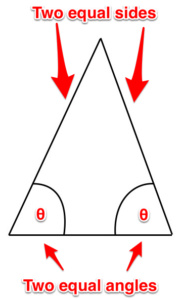
Figura 10. Triángulo isósceles

Triángulo equilátero. Los tres lados de este triángulo son iguales, y sus tres ángulos también son iguales.

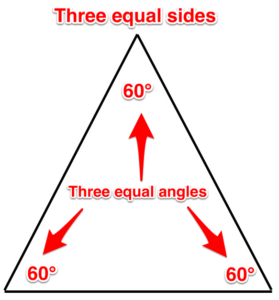
Figura 11. Triángulo equilátero

Triángulos similares. Cada uno de estos triángulos tiene lados de diferentes tamaños, pero comparten los mismos ángulos de tamaño.

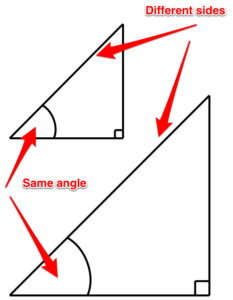
Figura 12. Triángulos similares

Entonces, ¿qué pasa con estos triángulos rectos de los que hablabas?

Un triángulo rectángulo es un triángulo que tiene un ángulo recto (igual a 90 grados). Esto quiere decir que los otros dos ángulos son complementarios, es decir, deben sumar a 90 grados.

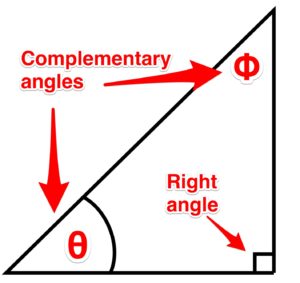
Figura 13. Ángulos complementarios.

Ok, entonces, ¿qué tiene que ver un triángulo rectángulo con lo eléctrico?

Bastante en realidad. En el mundo de la teoría eléctrica, tendremos que sumar valores. Llamamos a estas unidades vectores (más sobre el concepto de vectores en un capítulo posterior). Estos vectores se dirigen cada uno en una dirección diferente. De hecho, están a 90 grados el uno del otro. Cuando los sumamos, la suma de estos dos vectores termina siendo el punto entre los dos lados.

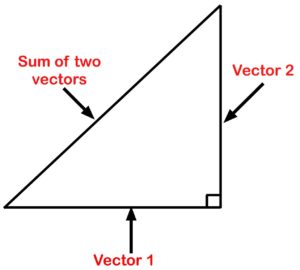
Figura 14. Triángulo vectorial

Debido a que no se dirigen en la misma dirección (van en direcciones que están a 90 grados entre sí) no podemos sumarlas normalmente. Tienen que agregarse vectorialmente. ¿Cómo se hace esto? Me alegra que lo hayas preguntado.