1.6: Triángulos de potencia e impedancia
- Page ID
- 151418
¿Qué está pasando aquí?
Este es el punto en el que voy a pedirte que tomes mi mano y confíes en mí. Bien, no tienes que tomarme la mano, pero sí tienes que confiar en mí. Vamos a empezar a usar algunos términos antes de entrar totalmente en la teoría detrás de ellos. Prometo que profundizaremos en estos conceptos en futuras lecciones.
Triángulos de impedancia
Cuando se trata de circuitos de CC lo único que se opone a la corriente es la resistencia en el circuito.
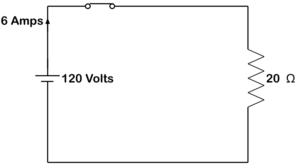
Figura 20. Circuito resistivo de CC
Como aprenderemos en unidades posteriores, AC agrega un componente que también se opone a la corriente. Esto se llama reactancia y corre 90 grados a la resistencia del circuito. Esto significa que no es posible sumarlos aritméticamente; tiene que hacerse usando el teorema de Pitágoras. Cuando se suman estos dos juntos, se obtiene una oposición total al flujo de corriente llamada impedancia.
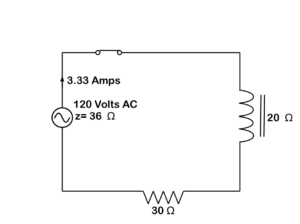
Figura 21. Circuito inductivo de CC
El triángulo que se crea al sumar la resistencia a la reactancia se conoce como triángulo de impedancia.

Figura 22. Triángulo de impedancia
En un triángulo de impedancia, la resistencia (r) está siempre en la parte inferior del triángulo, la reactancia (x) siempre va de lado y la hipotenusa es siempre la impedancia (z).
Triángulos de potencia
Cuando se trata de un circuito puramente resistivo, la potencia que se disipa es en forma de calor o luz y se mide en vatios y se conoce como potencia verdadera o activa. Es un producto de I 2 R.
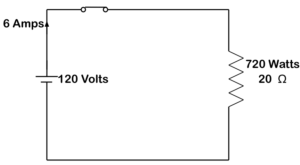
Figura 23. Circuito de potencia resistiva
En un circuito de CA con inductancia, los vatios siguen presentes. También hay una potencia reactiva presente a medida que la corriente pasa a través de la reactancia. Esta potencia se llama potencia reactiva y también se llama potencia sin vatio o cuadratura. Su unidad es la Vars.
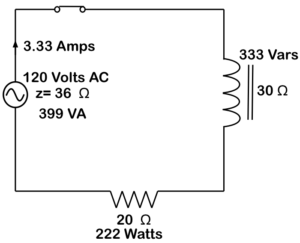
Figura 24. Circuito de potencia inductiva
Al igual que el triángulo de impedancia, no podemos simplemente sumar las dos potencias juntas para obtener potencia general. Deben agregarse usando el teorema de Pitágoras. Su suma es igual a la potencia aparente (VA).

Figura 25. Triángulo de poder
A la hora de calcular la potencia reactiva, todavía podemos usar las fórmulas de potencia. Sólo tenemos que utilizarlos con reactancia en lugar de resistencia.
- I 2 X = Vars
- E 2 (voltaje del inductor) /X = Vars
- I x E (voltaje inductor) = Vars
Recuerda
Al construir un triángulo de impedancia o potencia, el componente resistivo siempre va en la parte inferior del triángulo y el componente reactivo siempre va en el lado.


