2.13: Algoritmos y estructuras de datos
- Page ID
- 55105
Habiendo aprendido tantos conceptos de programación —variables y los datos a los que se refieren, funciones, bucles, etc.— sería una pena no hablar de algunos de los métodos sorprendentes y elegantes que habilitan. Los estudiantes de informática pasan años aprendiendo sobre estos temas, y los temas de este capítulo subyacen a gran parte de la bioinformática.
Comenzaremos con algoritmos, que según un libro clásico sobre el tema —Introducción a los algoritmos de Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest y Clifford Stein— son:
cualquier procedimiento computacional bien definido que tome algún valor, o conjunto de valores, como entrada y produzca algún valor, o conjunto de valores, como salida.
Con una definición tan amplia, toda la codificación Python que hemos hecho podría clasificarse con precisión como práctica en algoritmos. La palabra “algoritmo”, por cierto, deriva del nombre del matemático persa del siglo VIII al-Khwārizmī, quien desarrolló enfoques sistemáticos para resolver ecuaciones (entre otros logros). Aunque la mayor parte del código funcional puede caracterizarse como un algoritmo, los algoritmos generalmente implican algo más que recopilar datos y se emparejan con problemas bien definidos, proporcionando una especificación de qué son las entradas válidas y cuáles deben ser las salidas correspondientes. Algunos ejemplos de problemas incluyen:
- Dada una lista de
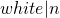 números en orden arbitrario, devuélvala o una copia de la misma en orden ordenado. (El problema de la “clasificación”.)
números en orden arbitrario, devuélvala o una copia de la misma en orden ordenado. (El problema de la “clasificación”.) - Dada una lista de
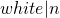 números en orden ordenado y un número de consulta
números en orden ordenado y un número de consulta q, devuelveTruesiqestá presente en la lista yFalsesi no lo está. (El problema de la “búsqueda”.) - Dadas dos cadenas de longitud
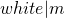 y
y 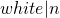 , alinearlas una contra la otra (insertando guiones donde sea necesario para hacerlas de la misma longitud) para maximizar una partitura basada en las coincidencias de caracteres. (El problema de “alineación de cadenas”).
, alinearlas una contra la otra (insertando guiones donde sea necesario para hacerlas de la misma longitud) para maximizar una partitura basada en las coincidencias de caracteres. (El problema de “alineación de cadenas”).

Claramente, algunos problemas, como el problema de alineación de cuerdas, son de especial interés para los científicos de la vida. Otros, como clasificar y buscar, son ubicuos. No importa a quién le importe el problema, un buen algoritmo para resolverlo debería hacerlo de manera eficiente. Por lo general, “eficientemente” significa “en poco tiempo”, aunque con los grandes conjuntos de datos producidos por las modernas tecnologías de secuenciación de ADN, a menudo también significa “usar una pequeña cantidad de memoria”.
La mayoría de los problemas bioinformáticos como la alineación de cuerdas requieren métodos bastante sofisticados construidos a partir de conceptos más simples, por lo que comenzaremos con el tema introductorio habitual para el diseño y análisis de algoritmos: la clasificación. Después de todo, alguien tuvo que escribir la función sort () de Python para listas, y forma una buena base para el estudio.
Considera una pequeña lista de cinco números, en orden sin clasificar.

¿Qué código podríamos escribir para ordenar estos números? Sea lo que sea, podría tener sentido ponerlo en una función que tome una lista sin clasificar y devuelva una copia de la misma en orden ordenado (para mantenerse consistente con el uso de Python del principio de separación de comando-consulta). Para comenzar, haremos una copia de la lista, y luego tendremos la función simplemente “arreglar” algunos de los números fuera de orden en esta copia mirando una ventana deslizante de tamaño 2, pares de números adyacentes, y cambiando su ubicación si están fuera de servicio.

El simple hecho de arreglar un puñado de pares de esta manera no dará como resultado que se ordene la lista, pero debería ser obvio que debido a que los pares de arreglos se superponen, el número más grande habrá encontrado su camino hasta la última posición. En cierto sentido, “burbujeó” hasta la cima. Si tuviéramos que repetir este proceso, el número de segundo a mayor también debe encontrar su camino hacia el lugar correcto. De hecho, si repetimos este proceso tantas veces como haya números, la lista estará completamente ordenada.


Este algoritmo de clasificación se conoce cariñosamente como “bubblesort”. En un sentido rudo, ¿cuántas operaciones realizará este algoritmo, en el peor de los casos, para una lista de tamaño![]() ? Supongamos que la sentencia if siempre encuentra
? Supongamos que la sentencia if siempre encuentra True, y los números necesitan ser intercambiados. En este caso, cada operación del bucle interno requiere cinco o así “pasos de tiempo” (cuatro asignaciones y una verificación if). El bucle interno corre![]() tiempos (si hay
tiempos (si hay![]() números), que a su vez se repiten
números), que a su vez se repiten![]() veces en el bucle externo. El paso de copia para producir la nueva lista
veces en el bucle externo. El paso de copia para producir la nueva lista c_nums también usa![]() pasos, por lo que el número total de operaciones básicas es, más o menos,
pasos, por lo que el número total de operaciones básicas es, más o menos,
\ [n (n-1) 5 + n = 5n^ {\ textcolor {blanco} {\ sombrero {\ textcolor {negro} {2}}} - 4n\.\]” title="Rendido por Quicklatex.com” src=” https://bio.libretexts.org/@api/deki...a1f374d_l3.png "/>
Sin embargo, al analizar el tiempo de ejecución de un algoritmo, solo nos importan las “cosas grandes”.
Notación de orden
Al calcular el tiempo de ejecución de un algoritmo, solo nos importan los términos de orden superior, y tendemos a ignorar constantes que no están relacionadas con el “tamaño” de la entrada. Decimos que el tiempo de ejecución es orden del término de orden más alto (sin constantes), que denotamos con mayúscula![]() :
:![]() is
is![]()
Leemos esto como “cinco![]() al cuadrado menos cuatro
al cuadrado menos cuatro![]() es orden
es orden![]() al cuadrado” o “cinco
al cuadrado” o “cinco![]() al cuadrado menos cuatro
al cuadrado menos cuatro![]() es grande oh
es grande oh![]() cuadrado”. Debido a que este tiempo de ejecución habla de un algoritmo en particular, también podríamos decir “bubblesort es orden
cuadrado”. Debido a que este tiempo de ejecución habla de un algoritmo en particular, también podríamos decir “bubblesort es orden![]() al cuadrado”. La notación Big-O implica que, aproximadamente, un algoritmo se ejecutará en un tiempo menor o igual que la ecuación interpretada como una función del tamaño de entrada, en el peor de los casos (ignorando constantes y términos pequeños).
al cuadrado”. La notación Big-O implica que, aproximadamente, un algoritmo se ejecutará en un tiempo menor o igual que la ecuación interpretada como una función del tamaño de entrada, en el peor de los casos (ignorando constantes y términos pequeños).
El análisis en el peor de los casos supone que tenemos mala suerte con cada entrada, pero en muchos casos el algoritmo podría funcionar más rápido en la práctica. Entonces, ¿por qué hacemos análisis en el peor de los casos? Primero, le da al usuario de un algoritmo una garantía: nadie quiere escuchar que el software podría usar cierta cantidad de tiempo. Segundo, si bien a veces es posible hacer análisis de casos promedio, requiere conocimiento de la distribución de los datos de entrada en la práctica (lo cual es raro) o técnicas de análisis más sofisticadas.
¿Por qué usamos la notación de orden para caracterizar el tiempo de ejecución del algoritmo, dejando pequeños términos y constantes? En primer lugar, aunque antes dijimos que cada operación básica es un “paso de computadora”, eso no es realmente cierto: la línea c_nums [index + 1] = leftnum requiere tanto una adición como una asignación. Pero nadie quiere contar cada ciclo de CPU individualmente, especialmente si el resultado no va a cambiar la forma en que comparamos dos algoritmos para grandes conjuntos de datos, que es el propósito principal de la notación de orden. Dejar términos constantes y términos de orden inferior tiene buen sentido matemático en estos casos. Para entrada lo suficientemente grande (es decir, todos![]() mayores que algún tamaño
mayores que algún tamaño ![]() ), incluso términos que parecen que harían una gran diferencia resultan no importar, como demuestra la siguiente comparación hipotética.
), incluso términos que parecen que harían una gran diferencia resultan no importar, como demuestra la siguiente comparación hipotética.
\ [\ begin {alineado} 0.01n^ {\ textcolor {blanco} {\ sombrero {\ textcolor {negro} {2}}} - 100n &> 200n^ {\ textcolor {blanco} {\ sombrero {\ textcolor {negro} {1.5}}} + 20n,\ texto {para} n >\ texto {algunos} c,\\ O (n^ {2} &) >O (n^ {1.5}),\\\ text {Tiempo Alg A} &>\ texto {Tiempo Alg B (para entradas grandes).} \ end {aligned}\]” title="Renderizado por Quicklatex.com” src=” https://bio.libretexts.org/@api/deki...0c800bc_l3.png "/>
(Técnicamente en lo anterior O (n^ {\ textcolor {blanco} {\ sombrero {\ textcolor {negro} {1.5}}}})" title="Procesado por Quicklatex.com" height="24" width="256" style="vertical-align: -4px;" src="https://bio.libretexts.org/@api/deki...67bc088_l3.png"> hay un abuso de notación; deberíamos decir que
![]() se
se![]() basa en la definición de la notación.) En este caso,
basa en la definición de la notación.) En este caso,![]() es mayor que
es mayor que![]() cuando
cuando![]() es mayor a 400,024,000 (que es el de este ejemplo
es mayor a 400,024,000 (que es el de este ejemplo ![]() ).
).
Entonces, aunque la notación de orden parece una forma difusa de ver la eficiencia de un algoritmo, es una forma rigurosamente definida y razonable de hacerlo. [1] Debido a que algunos lenguajes de programación son más rápidos que otros, pero solo por un factor constante (quizás el código C compilado es 100 veces más rápido que Python), ¡un buen algoritmo implementado en un lenguaje lento a menudo supera a un algoritmo mediocre implementado en un lenguaje rápido!
Ahora bien, un tiempo de ejecución de![]() no es muy bueno: el tiempo que se tarda en ordenar una lista de números crecerá cuadráticamente con el tamaño de la lista.
no es muy bueno: el tiempo que se tarda en ordenar una lista de números crecerá cuadráticamente con el tamaño de la lista.

![]() no es genial, pero para el problema de clasificación podemos hacerlo mejor, y volveremos al estudio de algoritmos y clasificación un poco más tarde. Primero, desviemos y hablemos de formas interesantes en las que podemos organizar los datos, utilizando variables y los objetos a los que se refieren.
no es genial, pero para el problema de clasificación podemos hacerlo mejor, y volveremos al estudio de algoritmos y clasificación un poco más tarde. Primero, desviemos y hablemos de formas interesantes en las que podemos organizar los datos, utilizando variables y los objetos a los que se refieren.
Estructuras de datos
Una estructura de datos es una organización para una recopilación de datos que idealmente permite un acceso rápido y ciertas operaciones sobre los datos. Ya hemos visto un par de estructuras de datos en Python: listas y diccionarios. Dada tal estructura, podríamos hacer preguntas como:
- ¿La estructura de datos mantiene sus elementos en un orden específico (como el orden ordenado)? Si usamos
.append ()para agregar elementos a las listas, las listas se mantienen en el orden en que se agregan los elementos. Si quisiéramos que la lista se mantuviera ordenada, tendríamos que asegurarnos de que los nuevos elementos se inserten en el lugar correcto. - ¿Cuánto tiempo se tarda en agregar un nuevo elemento? Para las listas de Python, el método
.append ()opera en el tiempo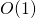 , es decir, se puede agregar un solo elemento al final, y el tiempo empleado no depende de qué tan grande sea la lista. Desafortunadamente, esto no será cierto si necesitamos mantener la lista ordenada, porque insertar en el medio requiere reorganizar la forma en que se almacenan los datos.
, es decir, se puede agregar un solo elemento al final, y el tiempo empleado no depende de qué tan grande sea la lista. Desafortunadamente, esto no será cierto si necesitamos mantener la lista ordenada, porque insertar en el medio requiere reorganizar la forma en que se almacenan los datos. - ¿Cuánto tiempo se tarda en encontrar el elemento más pequeño? Porque usando
.append ()agrega elementos al final de la lista, a menos que mantengamos la lista ordenada, necesitamos buscar en toda la lista el elemento más pequeño. Esta operación lleva tiempo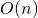 , donde
, donde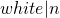 está la longitud de la lista. Sin embargo, si la lista está ordenada, solo toma
está la longitud de la lista. Sin embargo, si la lista está ordenada, solo toma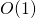 tiempo mirar al frente de la misma.
tiempo mirar al frente de la misma.
Hay compensaciones que podemos hacer al pensar en cómo usar las estructuras de datos. Supongamos, por ejemplo, que queríamos encontrar rápidamente el elemento más pequeño de una lista, incluso cuando se le agreguen elementos. Una posibilidad sería ordenar la lista después de cada adición; si lo hiciéramos, entonces el elemento más pequeño estaría siempre en el índice 0 para una rápida recuperación. Pero esto es mucho trabajo, ¡y el tiempo total dedicado a clasificar comenzaría a superar los beneficios de mantener la lista ordenada en primer lugar! Aún mejor, podríamos escribir una función que (1) inserte el nuevo elemento hasta el final y luego (2) lo burbujee hacia atrás a su ubicación correcta; solo se necesitaría uno de esos burbujeos para cada inserción, pero cada uno es una![]() operación (a menos que de alguna manera podamos garantizar que solo se agreguen elementos grandes).
operación (a menos que de alguna manera podamos garantizar que solo se agreguen elementos grandes).

Encontrar el artículo más pequeño es fácil, ya que sabemos que siempre está presente en el índice 0.
| Estructura | Insertar un artículo | Obtener el más pequeño |
|---|---|---|
| Lista Simple Ordenada | 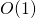 |
En cambio, hagamos algo mucho más creativo y construyamos nuestra propia estructura de datos desde cero. Si bien esta estructura de datos es un gran problema de crear por solo un pequeño beneficio, tiene sus usos y sirve como un bloque de construcción para muchas otras estructuras sofisticadas.
Listas Enlazadas Ordenadas
Nuestra estructura de datos, llamada “lista enlazada ordenada”, mantendrá una colección de artículos en orden ordenado, y hará el trabajo de insertar nuevos elementos en la ubicación correcta en ese orden. Estos elementos podrían ser enteros, flotantes o cadenas, cualquier cosa que pueda compararse con el operador < (que, recordar, compara cadenas en orden lexicográfico; como se discutió en capítulos anteriores, incluso podemos definir nuestros propios tipos de objetos que son comparables con > implementando . __lt__ (),. __eq__ () y métodos similares).
Para lograr esta tarea, vamos a hacer un uso intensivo de clases y objetos, y el hecho de que una variable (incluso una variable de instancia) es un nombre que hace referencia a un objeto.
La estrategia será tener dos tipos de objetos: el primero, al que llamaremos LinkedList, será el tipo principal de objeto con el que interactuarán nuestros programas (al igual que interactuamos con objetos Cromosoma en capítulos anteriores, mientras que los objetos SNP fueron tratados por los objetos Cromosómicos). El objeto LinkedList tendrá métodos como .insert_item () y .get_smaller (). Los otros objetos serán de tipo Node, y cada uno de estos tendrá una variable de instancia self.item que hará referencia al ítem almacenado por un Nodo individual. Entonces, dibujando solo los objetos en la RAM, nuestra lista ordenada enlazada de tres elementos (4, 7 y 9) podría verse así:

(Es poco probable que los objetos estén bien organizados de esta manera en RAM; los estamos mostrando en una línea solo para ilustración). Las flechas en esta figura indican que después de crear un nuevo objeto LinkedList llamado itemlist, esta variable es un nombre que hace referencia a un objeto, y cada objeto Node tiene una variable de instancia self.item que se refiere a un objeto “data” de algún tipo, como un entero o cadena. [2]
Ahora bien, si esta colección de objetos existiera como se muestra, no sería tan útil. Nuestro programa solo sería capaz de interactuar con el objeto itemlist, y de hecho no hay variables que se refieran a los objetos Node individuales, por lo que se eliminarían a través de la recolección de basura.
Aquí está el truco: si una variable de instancia es solo una variable (y por lo tanto una referencia a un objeto), podemos darle a cada objeto Node una variable de instancia self.next_n que hará referencia al siguiente nodo en la línea. Del mismo modo, el objeto LinkedList tendrá una variable de instancia self.first_n que hará referencia a la primera.

El último objeto Node self.next_n se refiere a None, un marcador de posición que podemos usar para permitir que una variable haga referencia a “nada aquí”. En realidad, None será el valor inicial para self.next_n cuando se cree un nuevo nodo, y tendremos que agregar métodos para get_next_n () y set_next_n () que nos permitan obtener o cambiar la variable next_n de Node a voluntad. La variable first_n de LinkedLists se inicializará de manera similar como None en el constructor.
Supongamos que tenemos esta estructura de datos en su lugar, y queremos agregar el número 2; este sería el nuevo elemento “más pequeño”. Para ello necesitaríamos ejecutar itemlist.insert_item (2), y este método consideraría las siguientes preguntas para manejar todos los casos posibles para insertar un ítem (usando if-statements):
- ¿Es
self.first_nigual aNone? Si es así, entonces el nuevo elemento es el único elemento, así que cree un nuevoNodoque contenga el nuevo elemento y establezcaself.first_nen ese nodo. - Si
self.first_nno es igual aNone:- ¿El nuevo artículo es más pequeño que el artículo de
self.first_n? Si es así, entonces (1) crea un nuevoNodoque contenga el nuevo elemento, (2) establezca sunext_nenself.first_n, y luego (3) establezcaself.first_nen el nuevo nodo. Aquí hay una ilustración para este caso:
- De lo contrario, el nuevo nodo no va entre el objeto
LinkedListy el primer objetoNode. En este caso, podríamos tratar el objetoself.first_ncomo si fuera él mismo unLinkedList, si tan solo tuviera un método.insert_item ().
- ¿El nuevo artículo es más pequeño que el artículo de
Este caso (b) es realmente el corazón de la estrategia de lista enlazada: cada objeto Node también tendrá un método .insert_item (). Además, el insert_item () de cada nodo seguirá la misma lógica que la anterior: si self.next_n es None, el nuevo nodo va tras ese nodo. Si no, el nodo necesita determinar si el nuevo nodo debe ir entre él y el siguiente nodo, o si debe “pasar el dólar” al nodo siguiente en la línea.
Ahora podemos pasar al código. Primero, aquí está el código para la clase LinkedList.

Las líneas resaltadas anteriormente son las ilustradas en el paso 2a y son cruciales; en particular, el orden en que se establecen las diversas variables marca la diferencia. ¿Qué pasaría si self.first_n = newnode fuera llamado antes newnode.set_next (self.first_n)? Perderíamos todas las referencias al resto de la lista: itemlist.first_n se referiría a newnode, .next_n del nuevo nodo se referiría a None, y ninguna variable se referiría al nodo que contiene 3 —se perdería en RAM y eventualmente basura colectado.
Como se mencionó anteriormente, la clase para un Nodo es bastante similar. De hecho, es posible construir listas enlazadas con un solo tipo de objeto, pero esto requeriría un nodo “ficticio” para representar una lista vacía de todos modos (tal vez almacenando None en su self.item).

Nuestra nueva estructura de datos es relativamente fácil de usar y se mantiene ordenada muy bien:

Métodos de lista enlazada
Esta idea de “pasar el dólar” entre nodos es bastante inteligente, y nos permite escribir consultas sofisticadas sobre nuestra estructura de datos con facilidad. Supongamos que quisiéramos preguntar si un ítem dado ya está presente en la lista.
Para resolver un problema como este, podemos pensar en cada nodo como implementar un procedimiento de decisión (usando un método, como .is_item_present (query)). El objeto de interfaz LinkedList devolvería False si su self.first_n es None (para indicar que la lista está vacía, por lo que el elemento de consulta no puede estar presente). Si su self.first_n no es None, llama a self.first_n.is_item_present (query), esperando que ese nodo devuelva True o False.

Para un nodo, el procedimiento de decisión es solo un poco más complejo:
- Compruebe si
self.itemes igual a laconsulta. Si es así, unTruepuede ser devuelto de manera segura. - De lo contrario:
- Si
self.next_nesNone, entonces se puede devolverFalse, porque si el buck se pasó al final de la lista, ningún nodo ha coincidido con laconsulta. - Si sí existe
self.next_n, por otro lado, solo pasa el dólar por la línea, y confía en la respuesta para volver, que se puede devolver.
- Si

Aquí hay una demostración rápida del uso (todo el script se puede encontrar en el archivo linkedlist.py):

Observe la similitud en todos estos métodos: cada nodo determina primero si puede responder al problema; si es así, calcula y devuelve la respuesta. Si no es así, comprueba si hay un nodo al que pasar el problema, y si existe, se pasa el dólar. Observe que en cada pase de dólar el método que se llama es el mismo, solo se le llama para un objeto diferente. Y cada vez que el “problema” general se hace más pequeño a medida que disminuye el número de nodos que quedan para pasar el dólar a.
¿Cuánto tiempo se tarda en insertar un ítem en una lista que ya es de longitud![]() ? Debido a que el nuevo elemento podría tener que ir al final de la lista, es posible que el dólar deba pasar
? Debido a que el nuevo elemento podría tener que ir al final de la lista, es posible que el dólar deba pasar![]() tiempos, lo que significa que una inserción es
tiempos, lo que significa que una inserción es ![]() . ¿Y qué hay de conseguir el elemento más pequeño? En el método
. ¿Y qué hay de conseguir el elemento más pequeño? En el método .get_smaller () de LinkedList, solo necesita determinar si self.first_n es None, y si no, devuelve el elemento almacenado en ese nodo. Porque no hay dólar que pasa, el tiempo lo es ![]() .
.
| Estructura | Insertar un artículo | Obtener el más pequeño |
|---|---|---|
| Lista Simple Ordenada | ||
| Lista Enlazada Ordenada | 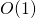 |
La creación de la estructura de listas enlazadas ordenadas no nos consiguió superar mucho una lista más sencilla mantenida en orden ordenada a través de burbujeo, pero las ideas implementadas aquí allanan el camino para soluciones mucho más sofisticadas.
Ejercicios
- ¿Cuánto tiempo tomaría insertar
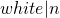 secuencias en una lista de Python y luego al final ordenarlas con bubblesort en el peor de los casos (usando notación de orden)?
secuencias en una lista de Python y luego al final ordenarlas con bubblesort en el peor de los casos (usando notación de orden)? - ¿Cuánto tiempo tardaría en insertar
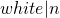 elementos en una lista enlazada ordenada que comience vacía, en el peor de los casos (usando notación de orden)? (Tenga en cuenta que la primera inserción es rápida, pero el segundo elemento puede tomar dos pasadas de compensación, el tercero puede tomar tres, y así sucesivamente).
elementos en una lista enlazada ordenada que comience vacía, en el peor de los casos (usando notación de orden)? (Tenga en cuenta que la primera inserción es rápida, pero el segundo elemento puede tomar dos pasadas de compensación, el tercero puede tomar tres, y así sucesivamente). - Agregue los métodos “pass the buck” a las clases
LinkedListyNodeque dan como resultado que cada elemento se imprima en orden. - Escriba métodos de “pasar el dólar” que provoquen que se imprima la lista de artículos, pero en orden inverso.
- Agregue métodos a las clases
LinkedListyNodepara que la lista enlazada pueda convertirse en una lista normal (en cualquier orden, aunque el orden inverso es lo más natural). Por ejemplo,print (itemlist.collect_to_list ())debería imprimir algo como['9', '3', '7'].
Divide y conquista
Hasta ahora, tanto el algoritmo (bubblesort) como la estructura de datos (lista enlazada ordenada) que hemos estudiado han sido de naturaleza lineal. Aquí, veremos cómo estas ideas se pueden extender de manera “bifurcada”.
Consideremos la lista enlazada ordenada de la última sección, la cual fue definida por una clase “controladora” (la LinkedList) y un número de Nodos casi idénticos, cada uno con una referencia a un objeto Node “next” en la línea. Siempre y cuando se siguieran ciertas reglas (por ejemplo, que la lista se mantuviera en orden ordenado), esto permitió que cada nodo tomara decisiones locales que dieron como resultado respuestas globales a las preguntas.
¿Y si le damos a cada nodo un poco más de potencia? En lugar de una sola variable de instancia self.next_n, ¿y si hubiera dos: una self.left_n y una self.right_n? Necesitaremos una regla correspondiente para mantener las cosas organizadas: los artículos más pequeños van hacia la izquierda y los artículos más grandes (o de igual tamaño) van hacia la derecha. Esta estructura de datos es el árbol binario bien conocido.

La ilustración anterior se ve bastante más complicada. Pero si inspeccionamos esta estructura de cerca, es bastante similar a la lista enlazada: [3] hay una clase controladora de BinaryTree, y en lugar de una variable de instancia self.first_n, tiene una variable de instancia llamada self.root_n, porque el nodo al que hace referencia es la “raíz” del árbol. Antes de que se haya insertado algún elemento, self.root_n será Ninguno. Al insertar un ítem, si self.root_n es None, el nuevo ítem va allí; de lo contrario, el buck se pasa necesariamente a self.root_n. Veremos por qué en un momento.

Ahora, para la clase Node, necesitaremos un constructor, así como métodos “get” y “set” tanto para left_n como right_n, que inicialmente se establecen en None.

¿Qué pasa con el método .insert_item () de un nodo? ¿Qué tipo de proceso de toma de decisiones debe suceder? El proceso es incluso más simple que para una lista enlazada ordenada. Si cada nodo siempre sigue la regla de que los elementos más pequeños se pueden encontrar a la izquierda y los elementos más grandes o iguales siempre se pueden encontrar a la derecha, entonces los nuevos elementos siempre se pueden insertar en la parte inferior del árbol. En el árbol de arriba, por ejemplo, un nodo que contiene 8 se colocaría a la derecha de (y “debajo”) del nodo que contiene 7. El proceso de decisión para un nodo es así como sigue:
- ¿El nuevo artículo para insertar es menor que nuestro
self.item? Si es así, el nuevo artículo va a la izquierda:- ¿Es
self.left_nigual aNone? Si es así, entonces necesitamos crear un nuevo nodo que contenga el nuevo elemento, y establecerself.left_nen ese nodo. - Si no, podemos pasar el dólar a
self.left_n.
- ¿Es
- De lo contrario, el artículo debe ser mayor o igual a
self.item, por lo que debe ir a la derecha:- ¿Es
self.right_nigual aNone? Si es así, entonces necesitamos crear un nuevo nodo que contenga el nuevo elemento, y establecerself.right_nen ese nodo. - Si no, podemos pasarle el dólar a
self.right_n.
- ¿Es
En la figura anterior de un árbol, 8 iría a la derecha de 7, 6 iría a la izquierda de 7, 18 iría a la derecha de 11, y así sucesivamente. La lógica para insertar un nuevo elemento es, por lo tanto, bastante simple, desde el punto de vista de un nodo:

El método restante a considerar es el .get_smaller () del árbol. En el caso de una lista enlazada, el ítem más pequeño (si estaba presente) era el primer nodo de la lista, y así se podía acceder sin pasar buck. Pero en el caso de un árbol binario, esto no es cierto: el elemento más pequeño se puede encontrar hasta la izquierda. El código para .get_smaller () en la clase Tree y la clase Node correspondiente refleja esto.


En el caso de un nodo, si self.left_n es None, entonces el ítem de ese nodo debe ser el más pequeño, porque puede suponer que el mensaje solo se pasó alguna vez hacia él a la izquierda. Código de uso similar al de la lista enlazada demuestra que esta maravillosa estructura (binarytree.py) realmente funciona:

La pregunta más interesante es: ¿cuánto tiempo se tarda en insertar un nuevo elemento en un árbol que ya contiene![]() elementos? La respuesta depende de la forma del árbol. Supongamos que el árbol es bonito y “tupido”, lo que significa que todos los nodos excepto los de la parte inferior tienen nodos a su izquierda y derecha.
elementos? La respuesta depende de la forma del árbol. Supongamos que el árbol es bonito y “tupido”, lo que significa que todos los nodos excepto los de la parte inferior tienen nodos a su izquierda y derecha.

El tiempo que se tarda en insertar un artículo es el número de veces que se necesita pasar el dólar para llegar al fondo del árbol. En este caso, en cada nodo, el número total de nodos en consideración se reduce a la mitad; primero ![]() , luego
, luego ![]() , luego
, luego ![]() , y así sucesivamente, hasta que haya un solo lugar al que el nuevo ítem podría ir. ¿Cuántas veces se
, y así sucesivamente, hasta que haya un solo lugar al que el nuevo ítem podría ir. ¿Cuántas veces se![]() puede dividir un número por la mitad hasta alcanzar un valor de 1 (o menor)? La fórmula es
puede dividir un número por la mitad hasta alcanzar un valor de 1 (o menor)? La fórmula es ![]() . Se necesita la misma cantidad de tiempo para encontrar el objeto más pequeño para un árbol tupido, porque la longitud hacia abajo por el lado izquierdo es la misma que cualquier otro camino hacia una “hoja” en el árbol.
. Se necesita la misma cantidad de tiempo para encontrar el objeto más pequeño para un árbol tupido, porque la longitud hacia abajo por el lado izquierdo es la misma que cualquier otro camino hacia una “hoja” en el árbol.
| Estructura | Insertar un artículo | Obtener el más pequeño |
|---|---|---|
| Lista Simple Ordenada | ||
| Lista Enlazada Ordenada | ||
| Árbol binario “tupida” | 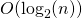 |
En general, el logaritmo de![]() es mucho más pequeño que
es mucho más pequeño que![]() él mismo, por lo que un árbol binario cambia algo de velocidad en la búsqueda del elemento más pequeño para la velocidad en la inserción.
él mismo, por lo que un árbol binario cambia algo de velocidad en la búsqueda del elemento más pequeño para la velocidad en la inserción.
Obsérvese, sin embargo, que la forma de un árbol depende del orden en que se inserten los elementos; por ejemplo, si se inserta 10 en un árbol vacío, seguido de 9, el 9 irá a la izquierda. Más insertando 8 lo pondrá todo el camino a la izquierda de 9. Así, es posible que un árbol no sea de hecho tupido, sino muy desequilibrado. Para un ejemplo extremo, si los números de![]() se insertaran en ese orden, el árbol se vería así:
se insertaran en ese orden, el árbol se vería así:

En este caso, el árbol se ha degenerado en una lista enlazada de orden inverso. Entonces, el tiempo de inserción (para 1, por ejemplo) es ![]() , y encontrar el elemento más pequeño también lo es, porque el árbol está muy desequilibrado en dirección hacia la izquierda. Desafortunadamente, en la práctica, no podemos garantizar el orden en que se insertarán los datos, y tales series de inserciones consecutivas no son infrecuentes en los datos del mundo real.
, y encontrar el elemento más pequeño también lo es, porque el árbol está muy desequilibrado en dirección hacia la izquierda. Desafortunadamente, en la práctica, no podemos garantizar el orden en que se insertarán los datos, y tales series de inserciones consecutivas no son infrecuentes en los datos del mundo real.
Las estructuras más sofisticadas llamadas árboles binarios “balanceados” tienen modificaciones en sus métodos de inserción que aseguran que el árbol se mantenga tupido, sin importar en qué orden se inserten los elementos. Esto es complicado, ya que requiere manipular la estructura del árbol después de las inserciones, pero la manipulación de la estructura en sí no puede tardar demasiado o se pierde el beneficio de la inserción. Ejemplos de árboles binarios balanceados incluyen los llamados árboles rojo-negros, y los árboles AVL (que llevan el nombre de Georgy Adelson-Velsky y Evgenii Landis, quienes los describieron por primera vez).
| Estructura | Insertar un artículo | Obtener el más pequeño |
|---|---|---|
| Lista Simple Ordenada | ||
| Lista Enlazada Ordenada | ||
| Árbol binario “tupida” | ||
| Árbol binario “no tupida” | ||
| Árbol binario balanceado | 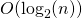 |
En la práctica, no hacemos una distinción entre árboles binarios “tupidos” y “unbushy”: los árboles simples de búsqueda binaria son tanto![]() para
para .insert_item () como para .get_smaller (), porque no podemos garantizar bushiness (recordemos que asumimos el peor de los casos al analizar un algoritmo) . Por lo tanto, las aplicaciones reales utilizan árboles AVL, árboles rojo-negros u otras estructuras de datos más sofisticadas.
Ejercicios
- Agregue los métodos “pass the buck” a
BinaryTreey su claseNodepara.print_in_order ()y.print_reverse_order (), haciendo que los elementos se impriman en orden ordenado e inverso, respectivamente. - Agrega métodos
.count_nodes ()que devuelven el número total de elementos almacenados en el árbol. ¿Cuánto tiempo lleva, en notación de orden? ¿Depende esto de si el árbol es tupido o no? Si es así, ¿cuál sería el tiempo de ejecución de un árbol tupido versus un árbol no tupido? - Agrega métodos
.count_leaves ()que devuelven el número total de “leaves” (nodos conNoneenleft_nyright_n). - Los árboles de búsqueda binarios se llaman así porque pueden determinar de manera fácil y eficiente si un elemento de consulta está presente. Agregue métodos
.is_item_present ()que devuelvenTruesi existe un elemento de consulta en el árbol yFalseen caso contrario (similar aLinkedList.is_item_present ()). ¿Cuánto tiempo lleva, en notación de orden? ¿Depende esto de si el árbol es tupido o no? Si es así, ¿cuál sería el tiempo de ejecución de un árbol tupido versus un árbol no tupido? - Modifique el código de árbol binario para que los elementos duplicados no se puedan almacenar en nodos separados.
Volver a Clasificación
Anteriormente dejamos el tema de la clasificación habiendo desarrollado bubblesort, un![]() método para ordenar una simple lista de ítems. Ciertamente podemos hacerlo mejor.
método para ordenar una simple lista de ítems. Ciertamente podemos hacerlo mejor.
Una de las características interesantes del método insert_item () utilizado por los nodos tanto en el árbol como en la lista enlazada es que este método, para cualquier nodo dado, se llama a sí mismo, pero en otro nodo. En realidad, no hay múltiples copias del método almacenadas en la RAM; más bien, se comparte un solo método entre ellos, y solo el parámetro self está cambiando realmente. Entonces, este método (que es solo una función asociada a una clase) en realidad se está llamando a sí mismo.
De manera relacionada, resulta que cualquier función (no asociada a un objeto) puede llamarse a sí misma. Supongamos que quisiéramos calcular la función factorial, definida como
\ [factorial (n) = n\ times (n-1)\ times (n-2)\ times\ dots\ times2\ times1\.\]” title="Rendido por Quicklatex.com” src=” https://bio.libretexts.org/@api/deki...8200ba4_l3.png "/>
Una de las características más interesantes de la función factorial es que se puede definir en términos de sí misma:
\ [factorial (n) =\ begin {cases} 1,\\ n\ times factorial (n-1),\ end {cases}\ begin {aligned} &\ text {if} n = 1,\\ &\ text {de lo contrario.} \ end {aligned}\]” title="Renderizado por Quicklatex.com” src=” https://bio.libretexts.org/@api/deki...c10a9a6_l3.png "/>
Si quisiéramos calcular factorial (7), una forma lógica de pensar sería: “primero, voy a computar el factorial de 6, luego multiplicarlo por 7”. Esto reduce el problema a la computación factorial (6), que lógicamente podemos resolver de la misma manera. Eventualmente vamos a querer calcular factorial (1), y darnos cuenta de que es solo 1. El código sigue esta lógica impecablemente:

Por sorprendente que pueda ser, este bit de código realmente funciona. [4] La razón es que el parámetro n es una variable local, y así en cada llamada de la función es independiente de cualquier otra variable n que pueda existir. [5] La llamada a factorial (7) tiene una n igual a 7, que llama factorial (6), que a su vez obtiene su propia n igual a 6, y así sucesivamente. Cada llamada espera en la línea subanswer = factorial (n-1), y solo cuando se alcanza factorial (1) los retornos comienzan a filtrarse de nuevo en la cadena de llamadas. Debido a que llamar a una función es una operación rápida (![]() ), el tiempo que se tarda en calcular
), el tiempo que se tarda en calcular factorial (n) es ![]() , uno por cada llamada y suma calculada en cada nivel.
, uno por cada llamada y suma calculada en cada nivel.

Esta estrategia, una función que se llama a sí misma, se llama recursión. Por lo general, hay al menos dos casos considerados por una función recursiva: (1) el caso base, que devuelve una respuesta inmediata si los datos son lo suficientemente simples, y (2) el caso recursivo, que calcula una o más subrespuestas y las modifica para devolver la respuesta final. En el caso recursivo, los datos sobre los que operar deben acercarse “más” al caso base. Si no lo hacen, entonces la cadena de llamadas nunca terminará.
Aplicar recursividad a ordenar elementos es relativamente sencillo. La parte más difícil será determinar qué tan rápido corre para una lista de tallas ![]() . Ilustraremos la estrategia general con un algoritmo llamado
. Ilustraremos la estrategia general con un algoritmo llamado quicksort, descrito por primera vez en 1960 por Tony Hoare.
Para una estrategia general, implementaremos la ordenación recursiva en una función llamada quicksort (). Lo primero que hay que verificar es si la lista es de longitud 1 o 0: si es así, simplemente podemos devolverla ya que ya está ordenada. (Este es el caso base del método recursivo.) Si no, elegiremos un elemento “pivot” de la lista de entrada; normalmente, este será un elemento aleatorio, pero usaremos el primer elemento como pivote para empezar. A continuación, dividiremos la lista de entrada en tres listas: lt, que contiene los elementos menores que el pivote; eq, que contiene los elementos iguales al pivote; y gt, que contiene elementos mayores que el pivote. A continuación, ordenaremos lt y gt para producir lt_sorting y gt_sorting. La respuesta, entonces, es una nueva lista que contiene primero los elementos de lt_sorting, luego los elementos de eq, y finalmente los elementos de gt_sorting.
Las partes interesantes del código a continuación son las líneas resaltadas: ¿cómo ordenamos lt y gt para producir lt_sorting y gt_sorting?

Podríamos usar la función ordenada () incorporada de Python, pero eso es claramente trampa. Podríamos usar bubblesort, pero al hacerlo, nuestra función sufriría el mismo límite de tiempo que para bubblesort (decimos “límite de tiempo” porque la notación de orden esencialmente proporciona un límite superior en el uso del tiempo). La respuesta es usar recursión: porque lt y gt deben ser ambos más pequeños que la lista de entrada, como subproblemas se están acercando al caso base, ¡y podemos llamar a quicksort () en ellos!

Intentemos analizar el tiempo de ejecución de quicksort (): ¿será mejor que, igual o peor que bubblesort? Al igual que con los árboles binarios cubiertos anteriormente, resulta que la respuesta es “depende”.
Primero, consideraremos cuánto tiempo tarda la función en ejecutarse, sin contar las subllamadas a quicksort (), en una lista de tamaño ![]() . El primer paso es escoger un pivote, que es rápido. A continuación, dividimos la lista de entrada en tres sublistas. Debido a que agregar a una lista es rápido, pero todos los
. El primer paso es escoger un pivote, que es rápido. A continuación, dividimos la lista de entrada en tres sublistas. Debido a que agregar a una lista es rápido, pero todos los![]() elementos deben agregarse a uno de los tres, el tiempo que se pasa en esta sección es
elementos deben agregarse a uno de los tres, el tiempo que se pasa en esta sección es ![]() . Después de las subllamadas, las versiones ordenadas de las listas deben agregarse a la lista de
. Después de las subllamadas, las versiones ordenadas de las listas deben agregarse a la lista de respuestas, y debido a![]() que hay cosas que agregar, también hay tiempo
que hay cosas que agregar, también hay tiempo ![]() . Así, sin contar las subllamadas recursivas, el tiempo de ejecución es
. Así, sin contar las subllamadas recursivas, el tiempo de ejecución es![]() más
más![]() que es
que es ![]() .
.
Pero ese no es el final de la historia, no podemos simplemente ignorar el tiempo que se tarda en ordenar las sublistas, aunque sean más pequeñas. Por el bien del argumento, supongamos que siempre tenemos “suerte”, y el pivote pasa a ser el elemento mediano de la lista de entrada, así que len (lt) y len (gt) son ambos aproximadamente ![]() . Podemos visualizar la ejecución de las llamadas a funciones como una especie de “árbol de llamadas”, donde el tamaño de los nodos representa qué tan grande es la lista de entrada.
. Podemos visualizar la ejecución de las llamadas a funciones como una especie de “árbol de llamadas”, donde el tamaño de los nodos representa qué tan grande es la lista de entrada.

Aquí, el “nodo” superior representa el trabajo realizado por la primera llamada; antes de que pueda terminar, debe llamar para ordenar la lista lt en la segunda capa, que nuevamente debe llamar para ordenar su propia lista lt, y así sucesivamente, hasta la capa inferior, donde se alcanza un caso base. El camino de ejecución se puede rastrear en la figura a lo largo de la línea. Para analizar el tiempo de ejecución del algoritmo, podemos señalar que la cantidad de trabajo realizado en cada capa es ![]() , por lo que la cantidad total de trabajo es este valor multiplicado por el número de capas. En el caso de que los pivotes dividan las listas aproximadamente por la mitad, el resultado es el mismo que el número de capas en el árbol binario tupido:
, por lo que la cantidad total de trabajo es este valor multiplicado por el número de capas. En el caso de que los pivotes dividan las listas aproximadamente por la mitad, el resultado es el mismo que el número de capas en el árbol binario tupido: ![]() . Así, en este escenario idealizado, el tiempo total de ejecución es
. Así, en este escenario idealizado, el tiempo total de ejecución es ![]() , que es mucho mejor que el
, que es mucho mejor que el![]() de bubblesort. [6]
de bubblesort. [6]

Esta ecuación supone que los pivotes dividen las listas de entrada más o menos a la mitad, lo que es probable que sea el caso (en promedio), si elegimos los pivotes al azar. Pero no elegimos al azar; usamos nums [0]. ¿Qué pasaría si la entrada a la lista pasara a estar ya ordenada? En este caso, el pivote siempre sería el primer elemento, lt siempre estaría vacío, y gt tendría un elemento menos. El “árbol de trabajo” también sería diferente.

En este caso “desafortunado”, el trabajo en cada nivel es aproximadamente ![]() , y así sucesivamente, por lo que el trabajo total es
, y así sucesivamente, por lo que el trabajo total es![]()
![]()
![]()
![]()
cuál es
![]() . ¿Significa esto que en el peor de los casos
. ¿Significa esto que en el peor de los casos quicksort () es tan lento como bubblesort? Desgraciadamente, sí. Pero algunas personas muy inteligentes han analizado quicksort () (asumiendo que el elemento pivote se elige al azar, en lugar de usar el primer elemento) y han demostrado que en el caso promedio el tiempo de ejecución es ![]() , y las posibilidades de un rendimiento significativamente peor son astronómicamente pequeñas. Además, un método similar conocido como “mergesort” opera garantizando una división uniforme 50/50 (de otro tipo).
, y las posibilidades de un rendimiento significativamente peor son astronómicamente pequeñas. Además, un método similar conocido como “mergesort” opera garantizando una división uniforme 50/50 (de otro tipo).
| Algorithm | Caso promedio | Peor de los casos |
|---|---|---|
| Bubblesort | ||
| Quicksort | ||
| Mergesort | 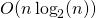 |
Usando selección aleatoria para pivot, quicksort () es rápido en la práctica, aunque también se utilizan frecuentemente algoritmos mergesort y similares. (.sort () y de Python usan una variante de mergesort llamada “Timsort.”) Aunque como se mencionó anteriormente, el análisis del peor de los casos es más frecuente en el análisis de algoritmos, sort ()quicksort () es una de las pocas excepciones a esta regla.
Estas discusiones sobre algoritmos y estructuras de datos pueden parecer esotéricas, pero deberían ilustrar la belleza y creatividad posibles en la programación. Además, los métodos definidos recursivamente y las sofisticadas estructuras de datos subyacen a muchos métodos en bioinformática, incluyendo el alineamiento de secuencias por pares, el alineamiento guiado por referencias y los modelos ocultos de Markov.
Ejercicios
- El primer paso para escribir
mergesort ()es escribir una función llamadamerge (); debe tomar dos listas ordenadas (juntas que comprenden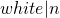 elementos) y devolver una versión ordenada fusionada. Por ejemplo,
elementos) y devolver una versión ordenada fusionada. Por ejemplo, merge ([1, 2, 4, 5, 8, 9, 10, 15], [2, 3, 6, 11, 12, 13])debe devolver la lista[1, 2, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 15], y debe hacerlo en el tiempo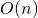 , donde
, donde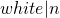 está el número total de elementos de ambas listas. (Tenga en cuenta que
está el número total de elementos de ambas listas. (Tenga en cuenta que .append ()en una lista de Python es tiempo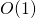 , al igual que las expresiones matemáticas como
, al igual que las expresiones matemáticas como c = a + b, pero otras operaciones de lista como.insert ()no lo son.)La función
mergesort ()primero debe dividir la lista de entrada en dos piezas de tamaño casi igual (por ejemplo,first_half = input_list [0:len (input_list) /2]); estas se pueden ordenar recursivamente conmergesort (), y finalmente la funciónmerge ()se puede usar para combinar las piezas ordenadas en una sola respuesta. Si todos los pasos en la función (sin contar las llamadas recursivas) son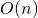 , entonces el tiempo total será
, entonces el tiempo total será 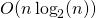 .
. Implementar merge ()ymergesort (). - Los números de Fibonacci (1, 1, 2, 3, 5, 8, 13, etc.) son, como los factoriales, definidos recursivamente:
\ [\ text {Fib} (n) =\ begin {cases} 1\\ 1\\\ text {Fib} (n - 1) +\ text {Fib} (n - 2)\ end {cases}\ begin {aligned} &\ text {if} n = 1,\\ &\ text {if} n = 2,\\ &\ text {de lo contrario.} \ end {aligned}\]” title="Renderizado por Quicklatex.com” src=” https://bio.libretexts.org/@api/deki...6eb643b_l3.png "/>
Escribe una función recursiva
fib ()que devuelva el número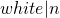 th de Fibonacci (
th de Fibonacci (fib (1)debería devolver1,fib (3)debería devolver2,fib (10)debería devolver55). - A continuación, escriba una función llamada
fib_loop ()que devuelva el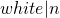 th Fibonacci usando un bucle simple. ¿Cuál es el tiempo de ejecución, en notación de orden, en términos de
th Fibonacci usando un bucle simple. ¿Cuál es el tiempo de ejecución, en notación de orden, en términos de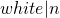 ? Compara cuánto tiempo se tarda en calcular
? Compara cuánto tiempo se tarda en calcular fib (35)versusfib_loop (35), y luego pruebafib (40)versusfib_loop (40). ¿Por qué crees quefib ()tarda tanto más? Intente dibujar los “árboles de llamada” parafib (1),fib (2),fib (3),fib (4),fib (5)yfib (6). ¿Podrías adivinar cuál es el tiempo de ejecución de esta función en notación de orden? ¿Te imaginas alguna manera de acelerarlo?
- Al analizar un algoritmo en Python, sin embargo, no todas las líneas son un solo paso computacional. Por ejemplo, Python tiene una función incorporada de sort
()para ordenar, y aunque no es tan lenta como bubblesort, toma mucho más de un paso ordenar millones de números. Si un algoritmo hace uso de una función comosorting (), también se debe considerar el tiempo de ejecución de esa (basado en el tamaño de la entrada dada). Una función que llama a nuestra función bubblesort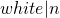 times, por ejemplo, se ejecutaría en el tiempo
times, por ejemplo, se ejecutaría en el tiempo 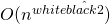 .
. - No hay ninguna razón por la que un objeto
Nodetampoco pueda contener otra información. Por ejemplo, los nodos podrían tener unself.snppara contener un objetoSNPtambién, siendoself.itemla ubicación del SNP, por lo que los SNP se almacenan en orden de sus ubicaciones. - Si ignoramos todas las referencias de los
nodos self.left_n(es decir, todo el lado izquierdo del árbol), entonces la rutaself.right_nde arriba a abajo a la derecha es una lista enlazada ordenada! Del mismo modo, la ruta de arriba a la inferior izquierda es una lista enlazada con clasificación inversa. - Los factoriales se pueden calcular fácilmente (y un poco más eficientemente) con un bucle, pero estamos más interesados en ilustrar el concepto de una función de autollamada.
- Adicionalmente, las operaciones de definir una función y ejecutarla son disjuntas, por lo que no hay nada que impida que una función se defina en términos de sí misma.
- Esta prueba es una prueba orientada visualmente, y no terriblemente rigurosa. Una prueba más formalizada desarrollaría lo que se conoce como una relación de recurrencia para el comportamiento del algoritmo, en forma de
, a resolver
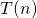 , representando el tiempo que se tarda en ordenar
, representando el tiempo que se tarda en ordenar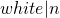 los ítems.
los ítems.


