9.4: Probabilidad y Análisis de Chi-Cuadrado

Observaciones de Mendel

Probabilidad: Cuadrados de Punnett pasados

Los Cuadrados Punnett son convenientes para predecir el resultado de cruces monohíbridos o dihíbridos. La expectativa de dos progenitores heterocigóticos es 3:1 en un solo cruce de rasgo o 9:3:3:1 en un cruce de dos rasgos. Realizar un cruce de tres o cuatro rasgos se vuelve muy desordenado. En estas instancias, es mejor seguir las reglas de probabilidad. Probabilidad es la probabilidad de que ocurra un evento expresada como una fracción o porcentaje. En el caso de un cruce monohíbrido, razón 3:1 significa que existe una probabilidad\(\frac{3}{4}\) (0.75) del fenotipo dominante con una probabilidad\(\frac{1}{4}\) (0.25) de un fenotipo recesivo.

Un solo dado tiene una probabilidad de 1 en 6 de ser un valor específico. En este caso, existe\(\frac{1}{6}\) la probabilidad de rodar un 3. Se entiende que enrollar un segundo troquel simultáneamente no está influenciado por el primero y por lo tanto es independiente. Este segundo dado también tiene\(\frac{1}{6}\) posibilidades de ser un 3.

Podemos entender estas reglas de probabilidad aplicándolas al cruce dihíbrido y dándonos cuenta de que llegamos al mismo resultado que los 2 monohíbridos Punnett Squares como con el único dihíbrido Punnett Square.

Este método de línea bifurcada para calcular la probabilidad de descendencia con diversos genotipos y fenotipos se puede escalar y aplicar a más características.

La prueba de Chi-Cuadrado

El estadístico χ ² se utiliza en genética para ilustrar si hay desviaciones de los resultados esperados de los alelos en una población. El supuesto general de cualquier prueba estadística es que no hay desviaciones significativas entre los resultados medidos y los pronosticados. Esta falta de desviación se denomina hipótesis nula (H ₀). El estadístico X ² utiliza una tabla de distribución para comparar los resultados con diferentes niveles de probabilidades o valores críticos. Si el valor X ² es mayor que el valor a una probabilidad específica, entonces se ha rechazado la hipótesis nula y se observó una desviación significativa de los valores predichos. Usando las leyes de Mendel, podemos contar fenotipos después de un cruce para compararlos con los predichos por probabilidades (o un Punnett Square).

Para poder utilizar la tabla, se debe determinar la rigurosidad de la prueba. Cuanto menor sea el valor p, más estrictas serán las estadísticas. También se calculan los Grados de Libertad (DF) para determinar qué valor en la tabla usar. Grados de Libertad es el número de clases o categorías que hay en las observaciones menos 1. dF=n-1

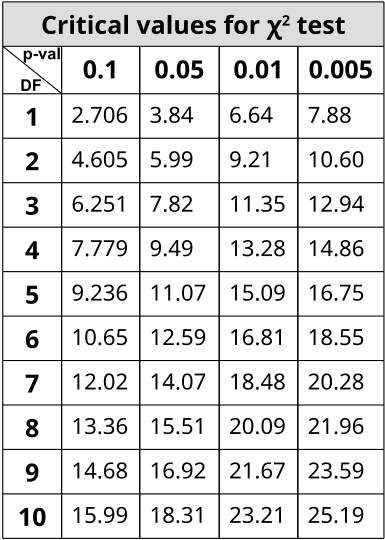
En el ejemplo del color y textura del grano de maíz, hay 4 clases: Púrpura y Suave, Morado y Arrugada, Amarillo y Suave, Amarillo y Arrugada. Por lo tanto, DF = 4 — 1 = 3 y eligiendo p < 0.05 para ser el umbral de significancia (rechazo de la hipótesis nula), el X ² debe ser mayor a 7.82 para estar desviándose significativamente de lo esperado. Con este ejemplo cruzado dihíbrido, se espera una relación de 9:3:3:1 en fenotipos donde 1/16 de la población son recesivos tanto para textura como para color, mientras que\(\frac{9}{16}\) de la población muestra tanto color como textura como dominante. \(\frac{3}{16}\)será dominante para un fenotipo mientras recesivo para el otro y el resto\(\frac{3}{16}\) será la combinación opuesta.

Con esto en mente, podemos predecir o tener resultados esperados usando estas proporciones. Tomando un recuento total de 200 eventos en una población, 9/16 (200) =112.5 y así sucesivamente. Formalmente, el valor de χ ² se genera sumando todas las combinaciones de:

\[\frac{(Observed-Expected)^2}{Expected}\]

Prueba de Chi-Cuadrado: ¿Esta Moneda Es Justa o Ponderada? (Actividad)

1. Todos en la clase deben voltear una moneda 2x y registrar el resultado (asume que la clase es 24).
2. Se espera que las monedas justas aterricen 50% cabezas y 50% colas.
   • El 50% de 48 resultados deben ser 24.
   • 24 cabezas y 24 colas ya están escritas en la columna “Esperado”.
3. Como clase, compile los resultados en la columna “Observado” (total de 48 volteos de monedas).
4. En la última columna, restar las cabezas esperadas de las cabezas observadas y cuadrarlas, luego dividirlas por el número de cabezas esperadas.
5. En la última columna, restar las colas esperadas de las colas observadas y cuadrarlas, luego dividirlas por el número de colas esperadas.
6. Suma los valores juntos de la última columna para generar el valor X ².
7. Compare el valor con el valor a 0.05 con DF=1.
   • Hay 2 clases o categorías (cabeza o cola), por lo que DF = 2 — 1 = 1.
   • ¿Los volteos de monedas fueron justos (no se desviaron significativamente de 50:50)?

Digamos que los tirados de monedas arrojaron 26 Cabezas y 22 Colas. ¿Podemos suponer que la moneda fue injusta? Si lanzamos una moneda un número impar de veces (por ejemplo 51), entonces esperaríamos que los resultados arrojarían 25.5 (50%) Cabezas y 25.5 (50%) Tails. Pero esto no es una posibilidad. Esto es cuando la prueba X ² es importante ya que delinea si 26:25 o 30:21 etc. están dentro de la probabilidad de una moneda justa.

Prueba de Chi-Cuadrado de Coloración y Textura del Núcleo en una Población F ₂ (Actividad)

1. A partir de los recuentos, se puede suponer qué fenotipos son dominantes y recesivos.
2. Rellene la categoría “Observado” con los recuentos correspondientes.
3. Rellene la “Relación Esperada” con 9/16, 3/16 o 1/16.
4. El número total del evento contado fue de 200, por lo que multiplicar la “Relación Esperada” x 200 para generar los campos “Número Esperado”.
5. Calcular el\(\frac{(Observed-Expected)^2}{Expected}\) para cada combinación de fenotipos
6. Sumar todos\(\frac{(Observed-Expected)^2}{Expected}\) los valores juntos para generar el valor X ² y comparar con el valor de la tabla donde DF=3.
7. ¿Rechazamos la Hipótesis Nula o fueron los números observados como esperábamos aproximadamente 9:3:3:1?
   • ¿Qué significaría si se rechazara la Hipótesis Nula? ¿Se puede explicar un caso en el que hemos observado valores que están significativamente alterados de lo que se espera?