13: Los efectos de la selección vinculada
- Page ID
- 58087
La deriva genética no es la única fuente de aleatoriedad en la dinámica de los alelos. Los alelos también experimentan fluctuaciones aleatorias en la frecuencia debido a que están presentes en un conjunto de antecedentes genéticos aleatorios con diferentes ajustes. Por ejemplo, cuando un alelo beneficioso surge a través de una sola mutación, surge sobre un fondo genético particular, es decir, un haplotipo particular (Figura\ ref {fig:HIV_Sweep} A). Imagínese esta mutación surgiendo en una región sin recombinación, o en un organismo donde el intercambio genético es raro. Si nuestro alelo benéfico se establece en la población, es decir, escapa de pérdida por deriva genética en esas primeras generaciones, comenzará a aumentar en frecuencia rápidamente. A medida que aumenta en frecuencia, también lo harán los alelos que sucedieron estar presentes en el haplotipo en el que surgió la mutación (si esos otros alelos son neutros o al menos no demasiado deletéreos). Estos otros alelos están llegando a 'autostop' a lo largo. Los alelos que no están en ese fondo particular son barridos de la población, por lo que el efecto neto de este barrido selectivo es eliminar la diversidad genética de la población. La diversidad eventualmente se recuperará, a medida que surjan nuevas mutaciones y algunas vayan variando lentamente en frecuencia. Pero a corto plazo, los barridos selectivos eliminan la variación genética de las poblaciones.
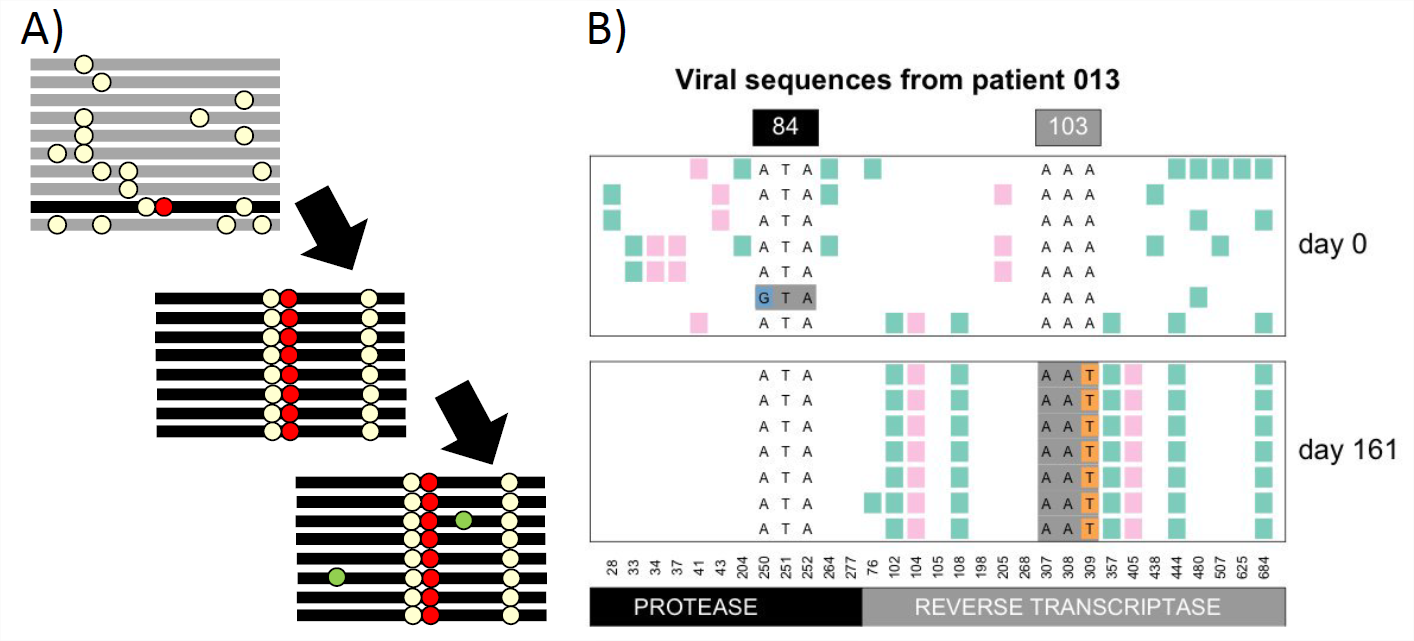
illiams548198 han visualizado barridos selectivos en VIH. En la Figura\ ref {fig:VIH_barrido} B) vemos un conjunto de haplotipos de VIH muestreados de un paciente antes y después de un barrido selectivo de una mutación farmacorresistente. El paciente está tomando un inhibidor de la retrotransposasa (Efavirenz), pero lamentablemente en 161 días ha surgido y se ha extendido una mutación farmacorresistente que cambia la proteína retrotransposasa del VIH. Observe cómo un haplotipo particular ahora se fija en la muestra, y queda poca diversidad genética, debido al efecto autostop del fuerte barrido selectivo de este alelo.
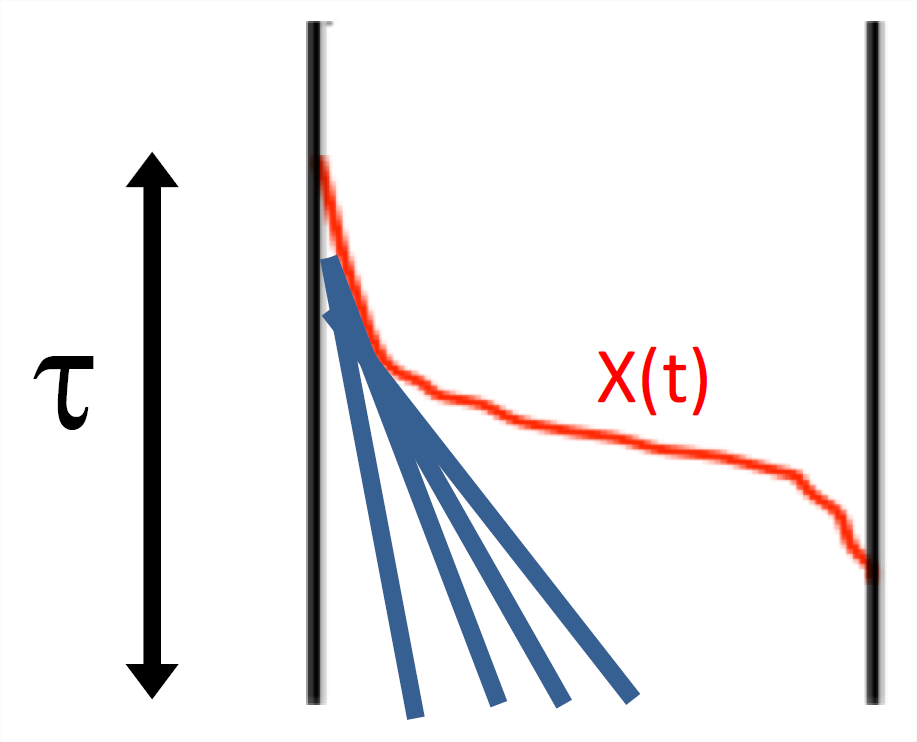
Para comprender mejor el autostop, primero imaginemos examinar la variación en un locus completamente vinculado a nuestro locus seleccionado, justo después de que nuestro barrido alcanzara la fijación. Los alelos neutros muestreados en este locus deben rastrear sus linajes ancestrales hasta el alelo neutro en cuyo fondo surgió inicialmente el alelo seleccionado (Figura\ ref {fig:no_recom_coal}). Esto se debe a que ese alelo neutro de fondo, que existió hace\(\tau\) generaciones, es el antepasado de toda la población en este locus totalmente ligado. Nuestros individuos que portan el alelo benéfico están, desde la perspectiva de estos alelos, experimentando una población en rápida expansión. Por lo tanto, un par de alelos neutros muestreados en nuestro locus neutro vinculado se verán obligados a fusionarse hace\(\approx \tau\) generaciones. Un alelo recién derivado con un coeficiente de selección aditivo\(s\) tardará\(\tau = 4\log(2N)/s\) varias generaciones en llegar a la fijación dentro de nuestra población (ver Ecuación\ ref {eq:diploid_fix_time}). Esta es una escala de tiempo muy corto en comparación con el tiempo promedio de coalescencia neutra de\(2N\) generaciones para un par de alelos. Por lo tanto, esperamos poca variación, ya que pocas mutaciones habrán surgido en estas ramas muy cortas, y las que lo hayan hecho probablemente serán singletones en nuestra muestra.
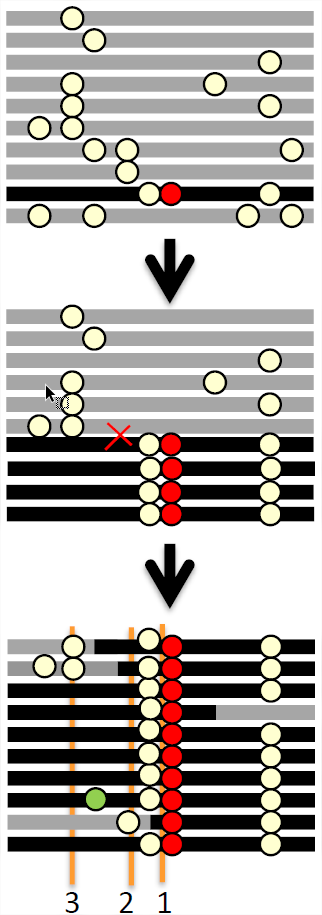
Ahora pensemos en un barrido en una región de recombinación. Nuevamente la mutación seleccionada surge sobre un haplotipo particular, y éste y su haplotipo comienzan a aumentar de frecuencia en la población (Figura\ ref {fig:sweep_haps}). Sin embargo, ahora pueden ocurrir eventos de recombinación entre haplotipos que portan y no portan el alelo seleccionado, en individuos que son heterocigotos para el alelo seleccionado. Estos eventos de recombinación permiten que los alelos que no estaban presentes en el haplotipo original seleccionado evitaran ser barridos de la población, y también desacoplar un poco el alelo seleccionado de los alelos autostop, evitando que muchos de ellos hicieran autostop hasta la fijación. Lejos del sitio seleccionado, la tasa de recombinación es lo suficientemente alta como para que los alelos que estaban presentes en el fondo original apenas lleguen a hacer autostop, ya que la recombinación rompe su asociación con el alelo seleccionado muy rápidamente.
¿Cómo se ven las genealogías coalesecentes en loci a varias distancias del sitio seleccionado? Bueno, cerca del sitio seleccionado todos nuestros alelos en la actualidad se remontan a un alelo ancestral común más reciente presente en ese haplotipo seleccionado, y así todos se ven obligados a fusionarse alrededor de\(\tau\) generaciones atrás (locus 1, ver Figura\ ref {fig:sweep_haps_coal}). Un poco más alejados del sitio seleccionado (locus 2), tenemos linajes que no trazan su ascendencia hasta el haplotipo original seleccionado, sino que descienden de haplotipos recombinantes que recombinaron en el barrido (el haplotipo segundo desde la parte inferior en la Figura\ ref {fig:sweep_haps_coal}). Estos linajes pueden fusionarse neutralmente con los otros linajes ancestrales en escalas de tiempo mucho más profundas y las mutaciones en estos linajes más profundos corresponden a la diversidad de pie presente en nuestra población antes del barrido. A medida que nos alejamos aún más del sitio seleccionado (locus 3), encontramos cada vez más linajes descendientes de haplotipos recombinantes que se fusionan neutralmente mucho más profundamente en el tiempo que\(\tau\), permitiendo que la diversidad se recupere a niveles de fondo a medida que nos alejamos del sitio seleccionado (ver Figura\ ref {fig:hitchhiking_reduction}).
Para modelar el patrón esperado de diversidad alrededor de un sitio seleccionado, podemos pensar en un par de alelos muestreados en un locus neutro a una\(c\) distancia de recombinación de nuestro sitio seleccionado. Nuestro par de alelos se verá obligado a fusionar\(\approx \tau\) generaciones si ninguno de ellos desciende de haplotipos recombinantes (Lado izquierdo de la Figura\ ref {fig:recom_coal}).
La probabilidad de que nuestros alelos en nuestro locus neutro desciendan del haplotipo ancestral en el que se produce el alelo seleccionado, es decir, que el alelo no descienda de un haplotipo recombinante es
\[p_{NR} = e^{-c \tau/2 }. \label{eqn:prob_no_recom_sweep}\]
Cuál es la intuición para este werll hay\(\tau\) generaciones en las que puede ocurrir una recombinación, por lo que aproximadamente la probabilidad de que no ocurra absolutamente ninguna recombinación es\((1-c)^{\tau} =\approx e^{-c\tau}\). ¿De dónde viene el factor de\(\frac{1}{2}\) in\ ref {eqn:prob_no_recom_barrido}? Bueno, para recombinar un alelo del fondo seleccionado la recombinación debe ocurrir en un heterocigoto para el alelo seleccionado, bajo un modelo aditivo un alelo neutro ligado a un alelo completamente barrido pasa en promedio\(\frac{1}{2}\) su tiempo en heteroziotes reduciendo así nuestra efectividad tasa de recombinación por un factor de dos (ver Apéndice 2 al final del capítulo para más detalles).
La probabilidad de que ninguno de nuestros linajes descienda de un haplotipo recombinante, y por lo tanto se vean obligados a unirse, es\(p_{NR}^2\) (suponiendo que se fusionen en un momento cercano a para\(\tau\) que se recombinen independientemente el uno del otro por tiempos\(< \tau\)). Si uno u otro de nuestros linajes desciende de un haplotipo recombinante, les tomará en promedio\(\approx 2N\) generaciones encontrar un ancestro común, ya que volvemos a nuestras probabilidades coalescentes neutras (Lado derecho de la Figura\ ref {fig:local_sweep_haps}). Así, el tiempo esperado hasta que nuestro par de linajes encuentre un ancestro común es
\[\mathbb{E}(T_2) = \tau \times p_{NR}^2 +(1-p_{NR}^2) (\tau +2N) \approx \left(1-p_{NR}^2 \right) 2N\]
donde esta última aproximación supone que\(\tau \ll 2N\). Entonces, la diversidad por pares esperada para los alelos neutros a una distancia de recombinación\(r\) alejada del barrido seleccionado (\(\pi_c\)) es
\[\mathbb{E}(\pi_c) = 2\mu \mathbb{E}(T_2) \approx \pi_0 \left(1-e^{-c\tau} \right) \label{eqn:pi_HH}\]
Así que la diversidad aumenta a medida que nos alejamos del sitio seleccionado, escalonándose lenta y exponencialmente a su expectativa neutral\(\pi_0\).
El patógeno de la malaria (Plasmodium falciparum) ha evolucionado la resistencia a los fármacos contra la malaria, a menudo por cambios en el gen dhfr. La Figura\ ref {fig:hitchhiking_malaria} muestra los niveles de diversidad genética (heterocigosidad) en un conjunto de marcadores que se mueven fuera del gen dhfr en un conjunto de secuencias de malaria resistentes a fármacos recolectadas en Tailandia. Vemos la característica caída en la diversidad alrededor del gen, con diversidad cero en varios de los loci muy cercanos al gen, lo que sugiere un fuerte barrido selectivo. Ajustando nuestro modelo simple de barrido a estos datos, estimamos que\(\tau \approx 40\) las generaciones, correspondientes a la fijación del alelo farmacorresistente en muy corto periodo de tiempo.
Para tener una idea de la escala física sobre la cual se reduce la diversidad, considere una región donde la recombinación ocurre a una velocidad\(c_{BP}\) por par de bases por generación, y un locus pares de\(\ell\) bases lejos del sitio seleccionado, de tal manera que\(c=c_{BP } \ell\) (donde \(c_{BP} \ell \ll 1\)así que no necesitamos preocuparnos por más de un evento de recombinación que ocurra por generación). Las tasas de recombinación típicas están en el orden de\(c_{BP} = 10^{-8}\). En la Figura\ ref {fig:hitchhiking_reduction} mostramos la reducción en la diversidad, dada por la Ecuación\ ref {eqn:pi_hh}, para dos coeficientes de selección diferentes.
Para que nuestro esperado nivel de diversidad se recupere a\(50\%\) de su expectativa neutral\(\mathbb{E}(\pi_c)/\theta=0.5\), se requiere una distancia física\(\ell^{*}\) tal que\(\log(0.5) = -x_{BP} \ell ^*\tau\), y por reordenamiento,
\[\ell^* = \frac{-\log(0.5)}{c_{BP} \tau }.\]
Como\(\tau\) depende inversamente de la selección\(s\) (Ecuación\ ref {eq:diploid_fix_time}), el ancho de nuestro valle de diversidad reducida depende de\(s/c_{BP}\). En igualdad de condiciones, esperamos que barridos o barridos más fuertes en regiones de baja recombinación tengan un mayor efecto de autostop. Por ejemplo, en una región genómica con una tasa de recombinación\(c_{BP}=10^{-8}\) bp\(^{-1}\) un coeficiente de selección\(s=0.1\%\) reduciría la diversidad sobre 10 de kb, mientras que un barrido de\(s=1\%\) afectaría a\(\sim\) 100kb.
identificó las bases genéticas del melanismo en la polilla salpicada (Biston betularia). Este alelo barrió hasta la fijación en partes del norte del Reino Unido; un caso clásico de adaptación a la contaminación industrial (hecho famoso por el trabajo de, ver y). La base genética del melanismo es un elemento transponible (TE) insertado en un gen de pigmentación. Encontró que la diversidad se suprime en una amplia región alrededor del TE. Específicamente, en el fondo del TE, se necesitan aproximadamente 200 kb en cualquier dirección para que los niveles de diversidad se recuperen al 50% de los niveles de todo el genoma.
Hechos aleatorios: En todas las polillas y mariposas solo los machos se recombinan; los cromosomas se transmiten sin recombinación en las hembras. La tasa de recombinación en machos es de 2.9 cm/MB. Las polillas salpimentadas tienen un tamaño poblacional efectivo de aproximadamente cien mil individuos. Kettlewell solía comer polillas cuando salía a recogerlas en el campo (comunicación personal, Art. Shapiro).
- Explique brevemente cómo este patrón ofrece más evidencia de que el alelo melánico fue favorecido por la selección.
- Usando esta información, y asumiendo que los efectos del alelo sobre la aptitud son aditivos, ¿cuál es su estimación de la edad del alelo?
- ¿Cuál es su estimación del coeficiente de selección que favorece este alelo melánico?
Otras señales de barridos selectivos
La señal primaria de un barrido selectivo recientemente completado es la reducción característica de la diversidad que rodea el sitio seleccionado. Sin embargo, los barridos dejan otras señales, y estas también se han utilizado a menudo para identificar loci en proceso de selección. Por ejemplo, los alelos neutros más alejados del sitio seleccionado pueden hacer autostop solo una parte del camino hacia la fijación si se produce la recombinación durante el barrido, lo que puede conducir a un exceso de alelos derivados de alta frecuencia a distancias intermedias del sitio seleccionado, un patrón que dura poco tiempo después de barrido. Además, a medida que los niveles de diversidad neutra se recuperan lentamente a través de una afluencia de nuevas mutaciones después de un barrido, existe un fuerte sesgo hacia alelos derivados de baja frecuencia, un patrón que persiste por muchas generaciones. El exceso de alelos raros, en comparación con un modelo neutro, puede ser capturado por estadísticas como la D de Tajima (que encontramos en nuestra discusión sobre la frecuencia de sitio neutral eqn\ ref {eqn_tajimas_D}). Así, una forma de buscar loci que han sido sometidos a barridos selectivos es calcular la D de Tajima a partir de datos en ventanas a lo largo del genoma y buscar fuertes salidas de la distribución nula.
[fig:local_sweep_haps]
También podemos usar comparaciones entre múltiples poblaciones para buscar evidencia de barridos ocurridos en una de las poblaciones, por ejemplo para identificar alelos involucrados en la adaptación local (ver\ ref {fig:local_sweep_haps}). Un barrido selectivo disminuirá la diversidad dentro de la población (\(H_S\)) que rodea el sitio seleccionado, sin afectar la diversidad entre diferentes poblaciones. Así, los barridos locales crean picos\(F_{\mathrm{ST}}\) entre poblaciones débilmente diferenciadas.
estudiaron los patrones de todo el genoma\(F_{\mathrm{ST}}\) entre poblaciones marinas y de agua dulce de espinas espinosas (Gasterosteus aculeatus), trazadas en la Figura\ ref {fig:local_sweep_stickleback}. Entre diferentes poblaciones marinas, no encontraron picos fuertes de\(F_{\mathrm{ST}}\); sin embargo, entre las comparaciones marinas y de agua dulce encontraron una serie de\(F_{\mathrm{ST}}\) picos altos que se replicaron sobre una serie de comparaciones entre agua dulce y marina. Identificaron una serie de nuevas regiones responsables de la adaptación de los lomos espinosos a ambientes de agua dulce y también una serie de loci previamente identificados en cruces entre poblaciones marinas y de agua dulce. Por ejemplo, el primer pico del Grupo de Vinculación IV incluye Ectodisplasina A (Eda), un gen involucrado en la pérdida adaptativa de blindaje en ambientes de agua dulce.
[fig:local_sweep_stickleback]
Barridos suaves a partir de múltiples mutaciones y variación de pie.
En nuestro modelo de barrido anterior, asumimos que la selección favoreció a un alelo beneficioso desde el momento en que ingresó a la población como una mutación de copia única (panel izquierdo, Figura\ ref {fig:soft_sweep_haps}). Sin embargo, cuando se activa una nueva selección de presión, múltiples mutaciones en el mismo gen pueden comenzar a barrer, de tal manera que ninguno de estos alelos barre hasta la fijación (panel central, Figura\ ref {fig:soft_sweep_haps}). Estos barridos que involucran múltiples mutaciones suavizan significativamente el impacto de la selección en la diversidad genómica, y así se llaman 'barridos suaves'.
[fig:soft_sweep_haps]
Otra forma en que se puede suavizar el impacto de un barrido es si nuestro alelo estuvo segregando en la población durante algún tiempo antes de que se volviera beneficioso. Ese tiempo adicional significa que nuestro alelo puede haberse recombinado en varios fondos de haplotipos, de manera que cuando cambian las presiones de selección, el alelo seleccionado barre en frecuencia en múltiples haplotipos diferentes (panel derecho, Figura\ ref {fig:soft_sweep_haps}). Detectar y diferenciar estos diferentes tipos de barridos es un área activa de investigación empírica y teoría en genómica poblacional (ver para una visión general de los desarrollos en esta área).
Los efectos genomáticos de la selección ligada.
¿Hasta qué punto los patrones de variación a lo largo del genoma y entre especies están conformados por la selección ligada, como los barridos selectivos? Podemos esperar identificar casos individuales de fuertes barridos selectivos a lo largo del genoma, pero ¿cómo contribuyen a patrones de variación más amplios?
Dos observaciones han desconcertado a los genetistas poblacionales desde el inicio de la genética de poblaciones moleculares. El primero es el nivel relativamente alto de variación genética observado en las especies más obligadamente sexuales. La teoría neutra de la evolución molecular se desarrolló en parte para explicar estos altos niveles de diversidad. Como vimos en el Capítulo\ ref {Chapter:Drift}, bajo un simple modelo neutro, con tamaño poblacional constante, debemos esperar que la cantidad de diversidad genética neutra escale con el producto del tamaño de la población y la tasa de mutación. La segunda observación, sin embargo, es el rango relativamente estrecho de polimorfismo entre especies con tamaños censales muy diferentes (ver Figura\ ref {fig:Leffer} y para una revisión reciente). Como destaca en su discusión sobre la paradoja de la variación, esta observación aparentemente contradice la predicción de la teoría neutra de que la diversidad genética debe escalar con el tamaño de la población censal. Hay una serie de explicaciones para la discrepancia entre los niveles de diversidad genética y el tamaño de la población censal. La primera es que el tamaño efectivo de la población (\(N_e\)) suele ser mucho menor que el tamaño del censo, debido a la alta varianza en el éxito reproductivo y frecuentes cuellos de botella (como se discute en el Capítulo\ ref {Capítulo:Deriva}). La segunda explicación importante, planteada por, es que los niveles neutros de diversidad también se reducen sistemáticamente por los efectos de la selección vinculada. En poblaciones grandes, los barridos selectivos y otras formas de selección ligada pueden llegar a dominar sobre la deriva genética como fuente de estocástica en las frecuencias alélicas, estableciendo potencialmente un límite superior a los niveles de diversidad.
[Fig:GW_Hitchhiking_reduction]
Una línea fuerte de evidencia para la acción de la selección ligada en la reducción de los niveles de polimorfismo es la correlación positiva entre la diversidad putativamente neutra y la recombinación observada en varias especies, ya que, siendo todo lo demás igual, la selección ligada debería eliminar la diversidad más rápidamente en regiones de baja recombinación. Por ejemplo, los niveles de diversidad de Drosophila melanogaster son mucho menores en regiones genómicas de baja recombinación (ver Figura\ ref {fig:GW_Hitchhiking_reduction}). Este patrón no puede explicarse por diferencias en la tasa de mutación entre regiones de recombinación baja y alta, ya que este patrón no se ve fuertemente en los datos de divergencia entre especies.
Estos patrones podrían reflejar la acción de barridos selectivos que ocurren de manera recurrente a lo largo del genoma. En la siguiente sección presentaremos un modelo de cómo los niveles de diversidad genética deben depender de la recombinación y la densidad de sitios funcionales bajo un modelo de barridos selectivos recurrentes. Sin embargo, otras formas de selección ligada pueden impactar la diversidad genética de manera similar. Por ejemplo, la diversidad genética ligada se pierde continuamente de las poblaciones naturales debido a la eliminación de haplotipos que portan alelos deletéreos; esto se denomina modelo de 'selección de fondo'. A continuación discutiremos el modelo de selección de antecedentes y sus predicciones básicas.
De manera más general, una amplia gama de modelos de selección predicen la eliminación de la diversidad neutra ligada a sitios seleccionados. Esto se debe a que los efectos reductores de diversidad de la alta varianza en el éxito reproductivo se agravan a lo largo de las generaciones cuando hay varianza heredable en la aptitud. Muchos modos diferentes de selección vinculada probablemente contribuyan a estos patrones de diversidad de todo el genoma; el desafío actual es cómo diferenciar entre estos diferentes modos.
Un simple modelo recurrente de barridos selectivos
Para explicar cómo una afluencia constante de barridos podría afectar los niveles de diversidad, aquí desarrollaremos un modelo de barridos selectivos recurrentes.
Imagínese que tomamos muestras de un par de alelos neutros en un locus a una\(c\) distancia genética de un locus donde se inician barridos dentro de la población a una tasa muy baja\(\nu\) por generación. El tiempo de espera entre barridos en nuestro locus se distribuye exponencialmente\(\sim Exp(\nu)\) (ver apéndice matemático\ ref {eqn:exp_rv_def}). Cada barrido transita rápidamente por la población en\(\tau\) generaciones, de tal manera que cada barrido se termina mucho antes del siguiente barrido (\(\tau \ll \frac{1}{\nu}\)).
Como antes, la posibilidad de que nuestro linaje neutro no se recombine fuera del barrido es\(p_{NR}\), tal que la probabilidad de que nuestro par de linajes se vea obligado a unirse por un barrido es\(e^{-c \tau}\). Por lo tanto, nuestros linajes tienen una probabilidad muy baja
\[\nu e^{-c \tau}\]
de ser forzado a coalescer por un barrido por generación. Si nuestros linajes no se fusionan debido a un barrido, se fusionan a una tasa neutra de\(\frac{1}{2N}\) por generación. Así, el tiempo de espera promedio hasta un evento coalescente entre nuestro par neutro de linajes debido a un barrido o un evento coalescente neutro es
\[\mathbb{E}(T_2) = \frac{1}{\nu e^{-c \tau} + \frac{1}{2N}}\]
Ahora imagina que los barridos no ocurren en una ubicación fija con respecto a nuestro locus de interés, sino que ahora ocurren uniformemente al azar a través de nuestro genoma. Los barridos se inician a una tasa muy baja de\(\nu_{BP}\) por par de bases por generación. La tasa de coalescencia debida a barridos en un locus\(\ell\) pares de bases alejados de nuestros loci neutros es\(2\nu_{BP} e^{-c_{BP} \ell \tau}\), donde el factor de dos proviene del hecho de que las bases pueden ser\(\ell\) pares de bases a la izquierda o a la derecha. Si nuestro locus neutro está en medio de un cromosoma que estira\(L\) pares de bases en cualquier dirección, la tasa total de barridos por generación que podrían obligar a nuestro par de linajes a unirse es
\[2\int_0^{L} \nu_{BP} e^{-c_{BP} \ell \tau} d \ell = \frac{2\nu_{BP}}{c_{BP} \tau} \left(1-e^{-c_{BP} \tau L} \right)\]
de manera que si\(L\) es muy grande (\(c_{BP} \tau L \gg 1\)), la tasa de coalescencia por generación debida a barridos es\(\frac{2\nu_{BP}}{c_{BP} \tau}\). La tasa total de coalescencia para un par de linajes por generación es entonces
\[\frac{2\nu_{BP}}{c_{BP} \tau}+\frac{1}{2N}\]
Así que nuestro tiempo promedio hasta que un par de linajes se unen es
\[\mathbb{E}(T_2) = \frac{1}{\frac{2\nu_{BP}}{c_{BP} \tau}+\frac{1}{2N}} = \frac{c_{BP}2N}{\frac{4N\nu_{BP}}{ \tau}+c_{BP}}\]
de tal manera que nuestra diversidad esperada por pares (\(\pi=2\mu\mathbb{E}(T_2)\)) en una región con tasa de recombinación\(r_{BP}\) que experimenta barridos a velocidad\(\nu_{BP}\) es
\[\mathbb{E}(\pi) = \pi_0 \frac{c_{BP}}{\frac{4N\nu_{BP}}{ \tau}+c_{BP}} \label{eqn:pi_GW_HH}\]
donde\(\pi_0\) esta nuestra diversidad esperada sin ningún barrido selectivo, (\(pi_0=\theta=4N\mu\)). La diversidad esperada aumenta con\(c_{BP}\), ya que mayores tasas de recombinación disminuyen la probabilidad de que un alelo neutro haga autostop junto con un barrido y, por lo tanto, se vea obligado a fusionarse por el barrido. La diversidad esperada disminuye con\(\nu_{BP}\), ya que una mayor densidad de sitios funcionales que experimentan barridos aumenta la probabilidad de ser vinculados a un barrido cercano. A medida que avanzamos hacia lo alto\(c_{BP}\), asumiendo que\(\nu_{BP}\) eso no aumenta con\(c_{BP}\), nuestro nivel de diversidad debe ser un nivel de diversidad genética de un sitio neutro completamente desvinculado a cualquier loci seleccionado.\(\theta\) Si asumimos que nuestro genoma experimenta una tasa constante de barridos de una fuerza dada, es decir, que\(\frac{4N\nu_{BP}}{ \tau}\) es una constante, podemos ajustar la variación\(\pi\) entre regiones que varían en su tasa de recombinación (\(c_{BP}\)) para estimar la tasa de una población de barridos recurrentes por par de bases. Un ejemplo de ajuste de esta curva a datos de Drosophila melanogaster se muestra en la Figura\ ref {fig:GW_Hitchhiking_reduction}; véase para un ejemplo temprano de ajuste de un modelo similar de autoestopas recurrente a dichos datos. El parámetro que nos da esta curva de mejor ajuste es\(\frac{4N\nu_{BP}}{ \tau} \approx 7 \times 10^{-9}\). Con una población efectiva de un millón y asumiendo que los barridos tardan mil generaciones en llegar a la fijación, encontramos que esto implica\(\nu_{BP} \approx 10^{-12}\). Así, una tasa realmente baja de barridos moderadamente fuertes, aproximadamente uno por megabase cada millón de generaciones, es todo lo que necesitamos para explicar la profunda caída en la diversidad observada en regiones del genoma con baja recombinación. Sin embargo, los barridos de alelos seleccionados positivamente no son la única causa de señales de selección enlazada en todo el genoma. La selección contra alelos deletéreos también puede impulsar estos patrones.
Selección de fondo
Las poblaciones experimentan una afluencia constante de mutaciones deletéreas en los loci funcionales mientras que la selección actúa para purgarlas de la población, evitando así sustituciones deletéreas y manteniendo la función en estos loci. Como se discutió en el Capítulo\ ref {Chapter:OneLocusSelection}, este equilibrio entre mutación y selección da como resultado un nivel constante de variación deletérea en la población. La selección constante frente a esta variación perjudicial tiene efectos sobre la diversidad en los sitios enlazados. Cada mutación deletérea surge al azar sobre un haplotipo en la población, y a medida que la selección purga esta mutación, elimina con ella cualquier alelo neutro que también estuviera en este haplotipo. Esta eliminación constante de alelos ligados de la población actúa para reducir la diversidad en las regiones que rodean los loci funcionales, un efecto conocido como selección de fondo (BGS).
¿Qué proporción de nuestros haplotipos están libres de mutaciones perjudiciales en una generación determinada, y así libres para contribuir a las generaciones futuras? Bueno, bajo equilibrio mutación-selección, un locus restringido con una tasa de mutación\(\mu\) hacia alelos deletéreos que experimentan un coeficiente de selección\(sh\) contra ellos en heterocigotos, dará como resultado\(\frac{\mu}{sh}\) cromosomas portadores del alelo deletéreo. Algunos de estos haplotipos pueden transmitirse a la siguiente generación, pero si están completamente vinculados al locus deletéreo, todos eventualmente se perderán porque portan una mutación deletérea en un sitio bajo restricción. Así, para un polimorfismo neutro completado ligado a un locus restringido, solo los\(2N(1-\frac{\mu}{sh})\) alelos llegan a contribuir a las generaciones futuras. Por lo tanto, el nivel de diversidad por parejas en una población constante debido a BGS en dicho locus será
\[\E[\pi] = 2 \mu \times 2N(1-\frac{\mu}{sh}) = \pi_0 (1-\frac{\mu}{sh})\]
donde\(\pi_0= 4N\mu\), el nivel de diversidad neutra por pares en ausencia de selección ligada.
[fig:bgs_cartoon]
Los efectos de la selección de fondo son más pronunciados en regiones de baja recombinación, donde los alelos neutros son menos capaces de recombinarse fuera del fondo de alelos deletéreos. Así, bajo selección de fondo, también esperamos ver diversidad reducida en regiones de menor recombinación.
Para un locus neutro que es una fracción de recombinación\(r\) lejos de un locus sujeto a restricción, el nivel de diversidad es
\[\E[\pi] = \pi_0 \left(1-\frac{\mu sh}{2(c+sh)^2} \right) \label{eqn:pi_loc_BGS_1}\]
A medida que nos alejamos de un locus que experimenta selección purificadora\(c\), aumentamos y la diversidad debería recuperarse. Por ejemplo, alejándonos de las regiones génicas en el genoma del maíz vemos que el nivel promedio de diversidad se recupera. Esto ocurre tanto en el maíz como en el teosinte, el progenitor silvestre del maíz. La caída en la diversidad alrededor de sitios no sinónimos es más fuerte en teosinte, quizás porque la deriva acelerada debido al cuello de botella en el maíz puede haber liberado alguna restricción en sitios donde alelos muy débilmente deletéreos segregados previamente en el equilibrio mutación-selección.
[fig:BGS_maíz]
Más generalmente, si un locus neutro está rodeado por\(L\) loci que experimentan selección purificadora a distancias de recombinación\(c_1,\cdots,c_L\), entonces componiendo la ecuación\ ref {eqn:pi_loc_bgs_1} a través de estos loci, la diversidad reducida esperada es aproximadamente
\[\E[\pi] = \pi_0 \prod_{i=1}^L \left(1-\frac{\mu sh}{2(c_L+sh)^2} \right) \approx \exp \left( \sum_{i=1}^L \frac{\mu sh}{2(c_i+sh)^2} \right) \label{eqn:pi_loc_BGS}\]
Para modelar un locus neutro promedio en una región genómica con una tasa de recombinación dada, podemos imaginar que nuestro locus neutro está situado en el centro de una región grande con tasa de recombinación total\(C\) y tasa de mutación deletérea total\(U\), donde\(U = \mu L\). Entonces nuestra expresión para diversidad, Ecuación\ ref {eqn:pi_loc_bgs}, simplifica a
\[\E[\pi] \approx \pi_0 \exp \left( \frac{-U}{(sh+C)} \right) \approx \pi_0 \exp \left( \frac{-U}{C} \right). \label{eqn:GW_BGS_1}\]
En esta última aproximación, suponemos que estamos viendo una región grande, con\(C \gg sh\). Tenga en cuenta que al igual que la carga genética, Ecuación\ ref {eqn:mut_load}, esta expresión depende únicamente de la tasa de mutación deletérea total. Cualquier dependencia del coeficiente de selección disminuye, ya que las mutaciones débilmente seleccionadas se segregan en la población a frecuencias más altas, pero también se eliminan de la población más lentamente, permitiendo que más del genoma se recombine del fondo deletéreo.
[fig:GW_BGS_Reducción]
Por primera vez para ajustar esto a los datos de todo el genoma, podríamos observar la diversidad en ventanas de longitud\(W\) bp (como en la Figura\ ref {fig:GW_BGS_REDUCTION}). Si asumimos que hay una tasa constante de mutación deletérea por par de bases,\(\mu_{BP}\), entonces\(U=\mu_{BP}W\). Además, si nuestra ventana genómica tiene una tasa de recombinación\(c_{BP}\) por par de bases, nuestra longitud genética total es\(R=c_{BP}W\). Haciendo estas sustituciones en la Ecuación\ ref {EQN:GW_BGS_1}, nuestro tamaño de ventana se cancela para dar
\[\E[\pi] \approx \pi_0 \exp \left(\frac{-\mu_{BP}}{c_{bp}} \right) \label{eqn:GW_BGS_2}\]
Mirando a través de ventanas que varían en su tasa de recombinación\(c_{BP}\), es decir, podemos ajustar la ecuación\ ref {eqn:gw_bgs_2} a los datos a estimar\(\mu_{BP}\). Un ejemplo de hacer esto a los datos de D. melanogaster se muestra en la Figura\ ref {fig:GW_bgs_reduction}, produciendo una estimación de la tasa de mutación deletérea de\(\mu_{BP}\approx 3.2 \times 10^{-9}\). Esto es aproximadamente en el mismo orden que la tasa de mutación por par de bases en D. melanogaster, por lo que esta estimación de la tasa de mutación deletérea es algo alta ya que requeriría que la mayor parte del genoma esté restringido, pero como primera aproximación no es terrible. Observe lo similar que es el ajuste a un modelo de autostop, sugiriendo que alguna combinación de BGS y autostop puede explicar la amplia relación entre diversidad y recombinación observada en D. melanogaster y otras especies.
[Fig:McVicker_BGS]
A medida que nuestras anotaciones de regiones funcionales del genoma han mejorado, también lo han hecho nuestros métodos para inferir la selección de fondo. Una versión más rigurosa de este análisis hoy incorporaría variación en la densidad de codificación entre ventanas en el parámetro\(\mu_{BP}\). Con anotaciones genómicas detalladas que muestran regiones codificantes y regiones restringidas no codificantes, también podemos ir más allá del simple análisis de patrones a gran escala. Por ejemplo, ajuste un modelo de selección de fondo para una diversidad de pares putativamente neutra a lo largo del genoma humano, usando la Ecuación\ ref {EQN:PI_LOC_BGS} para estimar el efecto de BGS en cada locus, pesando la distancia genética a todas las regiones codificantes circundantes y sitios no codificantes restringidos. Esto permitió estimar las tasas de mutación y los coeficientes de selección promedio que actúan contra alelos deletéreos en estas regiones del genoma. Este modelo de mejor ajuste también les permitió predecir niveles de diversidad a lo largo del genoma, una sección del cual se muestra en la figura\ ref {fig:McVicker_bgs}. Por lo tanto, las características a gran escala del polimorfismo a lo largo del genoma se describen bien mediante la selección de fondo (o por selección ligada de manera más general).
Las tasas de mutación deletéreas estimadas a partir del ajuste de un modelo de BGS volvieron a ser demasiado altas, como en el ejemplo anterior de Drosphila, sugiriendo que el BGS por sí solo no es suficiente para explicar todo el efecto de la selección ligada. Pero, ¿cómo entonces distinguimos el impacto de BGS del autostop?
Distinguir el impacto del hitchiking de la selección de antecedentes en datos de todo el genoma
Se han tomado una variedad de enfoques para comenzar a separar los efectos del autostop de la selección de antecedentes. Gran parte de la evidencia más fuerte que muestra los efectos de ambos proviene de Drosophila melanogaster y revisamos algunas de esas evidencias aquí. Se espera que el autostop tenga efectos sistemáticos sobre el espectro de frecuencia del sitio neutro, distorsionándolo hacia alelos menores raros, (reflejando la lenta recuperación de la diversidad después de un barrido). Por lo tanto, debemos esperar una distorsión de estadísticas sumarias como la D de Tajima en regiones de baja recombinación si el autostop está contribuyendo a la reducción de la diversidad en estas regiones. En D. melanogaster, existe un mayor sesgo hacia alelos raros en sitios putativamente neutros en regiones de baja recombinación; ver panel izquierdo de la Figura\ ref {fig:Tajimas_D_DN_PI}. Sin embargo, si bien este sesgo no se espera bajo modelos simples de fuerte selección de fondo.
[fig:tajimas_d_dn_pi]
Otra predicción del modelo de autostop, donde un alelo barre hasta la fijación, es que debe haber una sustitución funcional asociada a cada barrido. O, para darle la vuelta a eso, podríamos esperar ver un mayor impacto del autostop donde hay más sustituciones funcionales. Por ejemplo, las regiones que rodean las sustituciones no sinónimas deben tener niveles más bajos de diversidad, si una fracción alta de sustituciones no sinónimos son adaptativas. Nuevamente, este patrón se ve en D. melanogaster.
[Fig:Elyashiv_around_subs]
Empujando más esta idea, podemos ver la caída en la diversidad que rodea a una sustitución no sinónimo promediada a través de todas las sustituciones en el geno. encontró una caída más fuerte en la diversidad alrededor de las sustituciones no sinónimos que las sustituciones sinónimos. Ampliando el modelo de para adaptarse a un modelo de selección de fondo y autostop a la supuesta diversidad neutra a lo largo del genoma, encontraron que la caída en la diversidad alrededor de las sustituciones sinónimos proviene principalmente de BGS. Pero para explicar completamente la caída en la diversidad alrededor de las sustituciones no sinónimos, una proporción razonable de estas sustituciones no sinónimos tiene que haber sido acompañada de un barrido clásico (duro). Se estima que la mayoría de estos barridos se deben a una selección muy débil, con coeficientes de selección\(<10^{-4}\). Además, estimó una\(77\)\(89\%\) reducción en la diversidad neutra debido a la selección en sitios enlazados, y concluyó que ninguna ventana genómica estaba completamente libre de los efectos de la selección. Así, la selección ligada tiene un profundo efecto en algunas especies como Drosophila melanogaster.
Apéndice. La probabilidad de no recombinar del haplotipo seleccionado durante el barrido.
Sabemos que en la actualidad nuestro linaje neutro está ligado al alelo seleccionado. La probabilidad de que nuestro linaje, en alguna generación\(t\) atrás en el tiempo, esté en un heterocigoto es\(1-X(t)\), y la probabilidad de que ocurra una recombinación en ese individuo es\(r\). Entonces la probabilidad de que nuestro linaje neutro descienda de un haplotipo recombinante\(t\) generaciones atrás es
\[c (1-X(t))\]
Entonces la probabilidad (\(p_{NR}\)) de que nuestro linaje no descienda de un haplotipo recombinante de un evento de recombinación en las\(\tau\) generaciones que lleva nuestro alelo seleccionado para moverse por la población es
\[p_{NR}=\prod_{t=1}^{\tau} \big(1- c(1-X(j))\big)\]
Suponiendo que eso\(c\) es pequeño, entonces\(\left(1- c(1-X(t))\right) \approx e^{-r(1-X(t))}\), tal que
\[p_{NR}=\prod_{t=1}^{\tau} \left(1- c(1-X(t))\right) \approx \exp \left( -c\sum_{t=1}^{\tau} 1- X(t) \right) =\exp \left( -c \tau (1-\widehat{X}) \right)\]
donde\(\widehat{X}\) es la frecuencia promedio del alelo beneficioso derivado a lo largo de su trayectoria a medida que barre en frecuencia,\(\widehat{X} = \frac{1}{\tau} \sum_{t=1}^{\tau} X(t)\). Como nuestro alelo es aditivo, su trayectoria para frecuencias\(<0.5\) es la imagen especular de su trayectoria para frecuencias\(>0.5\), por lo tanto su frecuencia promedio\(\widehat{X} =0.5\). Esto simplifica nuestra expresión
\[p_{NR} = e^{-c \tau/2 }.\]
Cuando un alelo seleccionado inicialmente raro barre en frecuencia lleva consigo el fondo genético (haplotipo) en el que surgió. Los alelos que tienen la suerte de hacer autostop junto con el alelo seleccionado son arrastrados a alta frecuencia y la diversidad se agota por este efecto autostop.
En regiones de recombinación, la diversidad solo se suprime localmente por un barrido selectivo, ya que más lejos del sitio seleccionado los alelos pueden recombinarse encendido/apagado del barrido permitiendo que la diversidad persista en la población. La escala genómica del efecto hitchiking depende linealmente del tiempo que tarda el alelo seleccionado en barrer a través de la población e inversamente de la tasa de recombinación local. La inmersión característica en la diversidad se utiliza para encontrar barridos selectivos en escaneos genómicos y para estimar el tiempo y la fuerza de la selección.
Los barridos selectivos dejan un rango de otras señales genómicas que se han utilizado para identificarlas, incluyendo distorsiones en el espectro de frecuencias (un sesgo más extremo hacia alelos raros) y elevadas\(F_{ST}\) entre poblaciones.
Vemos una diversidad reducida en regiones de baja recombinación consistente con la mayor eliminación de diversidad en estas regiones debido al autostop recurrente. Sin embargo, este efecto de todo el genoma también es consistente con la selección de fondo, la eliminación de la diversidad ligada junto con alelos deletéreos.
[fig:branched_teosinte]
Maíz moderno derivado del teosinte, una planta maleza que crece en América del Sur y Central. Una notable diferencia fenotípica entre el teosinte y el maíz es que el teosinte es una planta tupida, mientras que el maíz crece principalmente hacia arriba. Un gen que ha sido implicado en esta transformación es tb1. secuenció una región alrededor de este gen para encontrar que los niveles de fondo de diversidad neutra disminuyen alrededor de este gen.
A) Se necesitan aproximadamente 300 pb para que la diversidad se recupere alejándose del barrido. estimación\(r = 4 \times 10^{-7}\) por par base. Estimar el tiempo (en años) desde que la variante de maíz seleccionada de tb1 surgió como una nueva mutación. El maíz es una planta anual, así que asuma 1 generación por año.
B) Supongamos que el tamaño efectivo de esta población diploide es\(N = 10^6\). ¿Cuál es el coeficiente selectivo de este alelo tb1?