6.1.4: Propiedad Focal de Elipses

Propiedad Focal de Elipses

En 1602, el astrónomo Johannes Kepler estaba trabajando en un problema para su jefe Tycho Brahe. Continuaba con un estudio centenario tratando de idear una fórmula que pudiera calcular las órbitas de los planetas, específicamente Marte en este caso. Trabajó durante años en el problema con la tecnología más avanzada de la época, pero nunca estuvo satisfecho con los resultados ya que nunca fueron realmente precisos o confiables.

Para simplificar sus cálculos, se topó con el concepto de que un planeta barre áreas iguales del espacio (en una figura en forma de rebanada de pastel con el sol en la punta) en iguales cantidades de tiempo, a pesar de las diferencias en la distancia del planeta del sol.

Durante los siguientes tres años intentó diseñar la ecuación perfecta para describir una órbita que se ajustara a esta y otras observaciones que estaba utilizando.

Por último, en 1605, se dio cuenta de que tenía la respuesta. Su realización/descubrimiento lo ubicaría firmemente como uno de los científicos más famosos de todos los tiempos.

¿De qué se dio cuenta?

---

Propiedad Focal de Elipses

Elipses no Centradas en el Origen

Para encontrar una ecuación para elipses centradas alrededor de otro punto, digamos\(\ (h, k)\), simplemente reemplace\(\ x\) con\(\ x−h\) y\(\ y\) con\(\ y−k\). Esto desplazará todos los puntos de la elipse hacia las\(\ h\) unidades de la derecha (o izquierda si\(\ h<0\)) y hacia arriba\(\ k\) (o hacia abajo si\(\ k<0\)). Entonces, la forma general para una elipse orientada horizontal o verticalmente es:

\(\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)

Está centrada sobre el punto\(\ (h,k)\). Si\(\ b<a\), la elipse está orientada horizontalmente y tiene focos\(\ \left(h+\sqrt{a^{2}-b^{2}}, k\right)\) y\(\ \left(h-\sqrt{a^{2}-b^{2}}, k\right)\) en su eje mayor horizontal. Si\(\ a<b\), está orientado verticalmente y tiene focos\(\ \left(h, k+\sqrt{a^{2}-b^{2}}\right)\) y\(\ \left(h, k-\sqrt{a^{2}-b^{2}}\right)\) en su eje mayor vertical.

---

Ejemplos

Ejemplo 1

Anteriormente, se le hizo una pregunta sobre el problema en el que estaba trabajando el astrónomo Johannes Kepler para su jefe, Tycho Brahe.

Solución

La comprensión de Kepler fue que, a pesar de que las había evitado deliberadamente durante mucho tiempo porque eran tan simples, las elipses eran la forma perfecta para hacer que todos sus cálculos se unieran.

Cuando un planeta orbita al sol (o cuando cualquier objeto orbita cualquier otro), toma un camino elíptico y el sol se encuentra en uno de los dos focos de la elipse. Las leyes de Kepler con respecto al movimiento planetario son lo suficientemente precisas como para producir cálculos modernos que todavía se utilizan para predecir el movimiento de los satélites artificiales en la actualidad.

Ejemplo 2

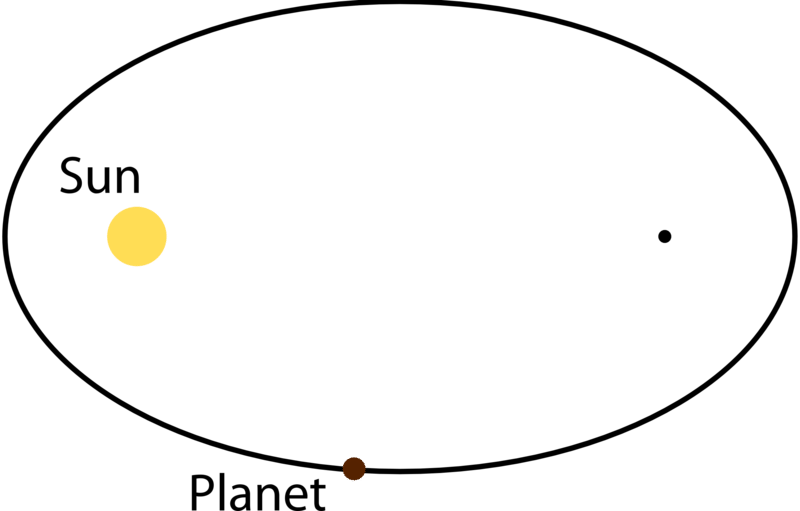
Explica por qué restar\(\ h\) del\(\ x\) −term y\(\ k\) del\(\ y\) −term en la ecuación para una elipse desplaza la elipse\(\ h\) horizontal y\(\ k\) verticalmente.

Solución

Si\(\ (x,y)\) es una solución para\(\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)

entonces\(\ (x+h, y+k)\) es una solución para\(\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)

Esto produce una gráfica que se desplaza horizontalmente por\(\ h\) y verticalmente por\(\ k\).

Ejemplo 3

Grafica la ecuación\(\ 4 x^{2}+8 x+9 y^{2}-36 y+4=0\).

Solución

Necesitamos obtener la ecuación en la forma de ecuación general anterior. El primer paso es agrupar todos los\(\ x\) términos y\(\ y\) términos, factorizar nuestros coeficientes principales de\(\ x^{2}\) y\(\ y^{2}\), y mover las constantes al otro lado de la ecuación:

\(\ 4\left(x^{2}+2 x\right)+9\left(y^{2}-4 y\right)=-4\)

Ahora, “completamos el cuadrado” agregando los términos apropiados a las\(\ x\) expresiones y a las\(\ y\) expresiones para hacer un cuadrado perfecto.

\(\ 4\left(x^{2}+2 x+1\right)+9\left(y^{2}-4 y+4\right)=-4+4+36\)

Ahora factorizamos y dividimos por los coeficientes para obtener:

\(\ \frac{(x+1)^{2}}{9}+\frac{(y-2)^{2}}{4}=1\)

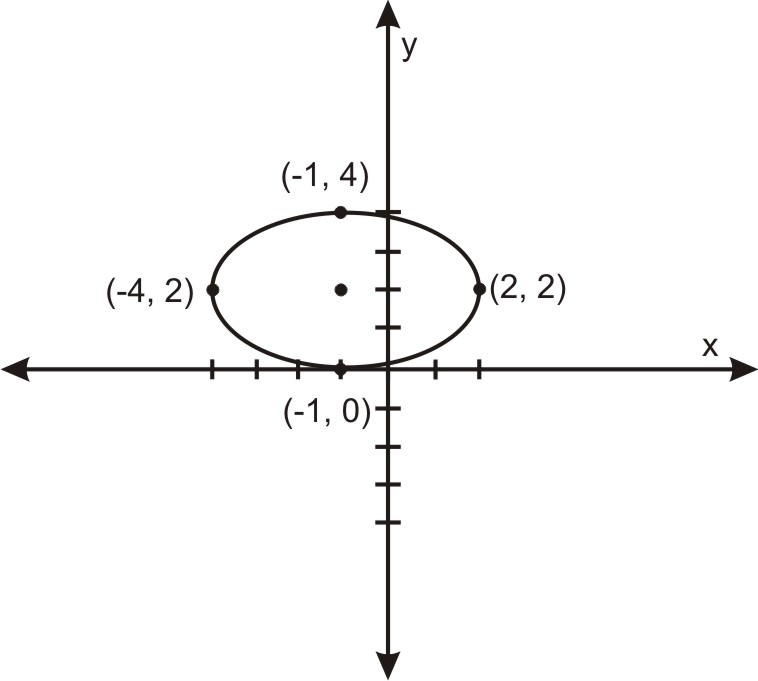
Y ahí lo tenemos. Una vez que está en esta forma, vemos que esta es una elipse centrada alrededor del punto (-1,2), tiene un eje mayor horizontal de longitud 3 y un eje menor vertical de longitud 2, y a partir de esto podemos hacer un boceto de la elipse:

Ejemplo 4

El Salón Nacional de Estatuas en el Edificio Capital de Estados Unidos es un ejemplo de una habitación en forma de elipse, a veces llamada “sala de eco”, que proporcionan una interesante aplicación a una propiedad de elipses. Si una persona susurra muy silenciosamente a uno de los focos, el sonido resuena de tal manera que una persona en el otro foco a menudo puede escucharlos con mucha claridad. Se rumorea que John Quincy Adams aprovechó esta propiedad para espiar conversaciones en esta habitación.

¿Cómo funcionan las Echo Rooms? ¿Qué tiene que ver con ello la forma elíptica de la habitación?

Solución

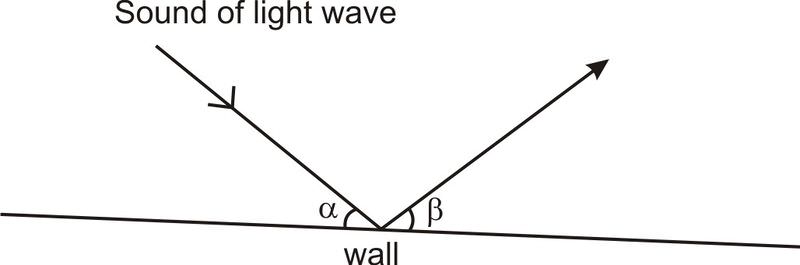
La propiedad de elipses que hace que funcionen las salas de eco se llama la “propiedad óptica”. Entonces, ¿por qué se hace eco, si se trata de una propiedad óptica? Bueno, los rayos de luz y las ondas sonoras rebotan de manera similar. En particular, ambos rebotan en las paredes en ángulos iguales. En el diagrama a continuación,\(\ α=β\).

Para un muro curvo, rebotan en ángulos iguales a la línea tangente en ese punto:

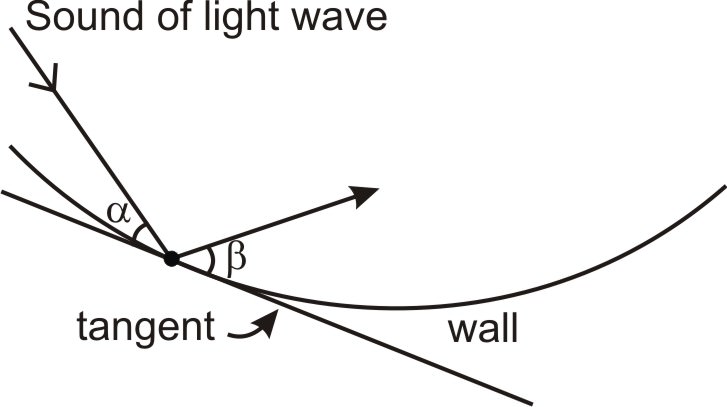
Entonces la “propiedad óptica” de las elipses es que las líneas entre un punto de la elipse y los dos focos forman ángulos iguales a la tangente en ese punto, o en otras palabras, los susurros provenientes de uno de los focos rebotan directamente a los otros focos. En el diagrama de abajo, para cada uno\(\ Q\) en la elipse,\(\ \angle \alpha \cong \angle \beta\).

Ejemplo 5

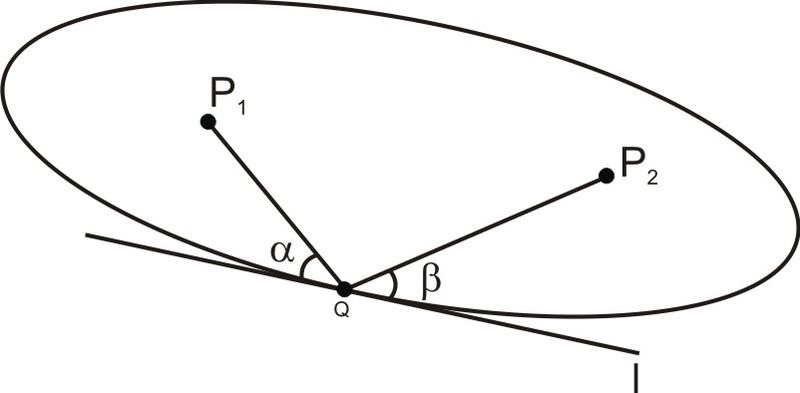
Aunque los planetas toman un camino elíptico alrededor del sol, estas elipses suelen tener una excentricidad muy baja, lo que significa que están cerca de ser círculos. El diagrama anterior exagera la forma elíptica de la órbita de un planeta. La órbita terrestre tiene una excentricidad de 0.0167. Su distancia mínima del sol es de 146 millones de km. ¿Cuál es su distancia máxima del sol? Si el diámetro del sol es de 1.4 millones de kilómetros, ¿ambos focos de la órbita terrestre se encuentran dentro del sol?

Solución

Recordemos que la excentricidad de una elipse es\(\ \varepsilon=\frac{\sqrt{a^{2}-b^{2}}}{a}\)

Supongamos que la órbita del sol es una elipse centrada en (0,0). Entonces podemos usar la distancia desde el origen hasta el foco\(\ \sqrt{a^{2}-b^{2}}\) para configurar las ecuaciones\(\ 146+146+2 \sqrt{a^{2}-b^{2}}=2 a\) y\(\ 0.167=\frac{\sqrt{a^{2}-b^{2}}}{a}\). Resolviendo obtenemos\(\ a=175.270, b=175.245\) y la distancia de (0, 0) a los focos,\(\ c\) =2.927 (todas las unidades están en millones de km). Finalmente la distancia máxima de la tierra al sol es de aproximadamente 152 millones de km. Por la ley de Kepler, sabemos que uno de los focos de su órbita está en el centro del sol. El otro focos está a 2 (2.927) =5.854 millones de kilómetros de distancia, por lo que está fuera del sol (¡pero no muy lejos!)

Ejemplo 6

¿Cuál es la suma de las distancias a los focos de los puntos en una elipse orientada verticalmente?

Solución

2b

Ejemplo 7

Intenta graficar la elipse:\(\ 3 x^{2}-12 x+5 y^{2}+10 y-3=0\). ¿Qué sale mal?

Solución

Después de completar el cuadrado, tenemos la suma de números positivos que equivalen a un número negativo. Esto es una imposibilidad, por lo que la ecuación no tiene soluciones.

Ejemplo 8

Grafica la elipse (puntos de trazado):\(\ 5 x^{2}-15 x-2 y^{2}+8 y-50=0\). ¿Qué es lo diferente aquí? Explica cómo crees que podría ser la gráfica de esta ecuación.

Solución

Después de completar la plaza, el\(\ x\) término y el\(\ y\) término son signos opuestos. Si trazas algunos puntos verás que la gráfica tiene dos secciones desconectadas. Esta clase de secciones cónicas se discutirá en la lección sobre hipérbolas.

---

Revisar

Grafica las siguientes elipses más avanzadas.

1. \(\ (x)^{2}+\frac{(y+2)^{2}}{9}=1\)
2. \(\ \frac{(x+2)^{2}}{4}+(y+2)^{2}=1\)
3. \(\ \frac{(x+2)^{2}}{9}+(y)^{2}=1\)
4. \(\ \frac{(x-1)^{2}}{9}+\frac{(y-4)^{2}}{16}=1\)
5. \(\ 4(x-1)^{2}+9(y)^{2}=36\)
6. \(\ (x+1)^{2}+\frac{(y-1)^{2}}{9}=1\)
7. \(\ (x-4)^{2}+\frac{(y+3)^{2}}{16}=1\)
8. \(\ \frac{(x)^{2}}{16}+\frac{(y)^{2}}{9}=1\)
9. \(\ 4(x+1)^{2}+(y-3)^{2}=16\)
10. \(\ (x+4)^{2}+\frac{(y-1)^{2}}{16}=1\)

Grafica las siguientes elipses de casos especiales.

11. \(\ (x+4)^{2}+(y+2)^{2}=4\)
12. \(\ (x+2)^{2}+(y)^{2}=16\)
13. \(\ (x-3)^{2}+(y-2)^{2}=1\)
14. \(\ (x+2)^{2}+(y-1)^{2}=9\)
15. \(\ (x-3)^{2}+(y-1)^{2}=9\)
16. ¿Qué tienen en común estas elipses?

Responde los siguientes problemas verbales.

17. Mientras que los caminos elípticos de los planetas son elipses que se aproximan estrechamente por círculos, los cometas y asteroides suelen tener órbitas que son elipses con excentricidad muy alta. El cometa Halley tiene una excentricidad de 0.967, y se encuentra a 54.6 millones de millas del sol en su punto más cercano, o “perihelio”. ¿Cuál es el punto más alejado que alcanza del sol?
18. Calcula el área de una elipse con la ecuación\(\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) (Sugerencia: usa un argumento geométrico que comienza con el área de un círculo).
19. Diseña la sala de eco más grande posible con las siguientes restricciones: Te gustaría espiar a alguien que estará a 3 m de la punta de la elipse. La habitación no puede tener más de 100 m de ancho en ninguna dirección. ¿A qué distancia de la persona a la que estás espiando estarás de pie?
20. No importa cuál sea la orientación de un palo, si trazas el camino que hace la sombra de la punta sobre una superficie plana, encontrarás que es una elipse. Describa por qué esto es cierto.

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.2.

---

Recursos

"frameborder="0" height="450px” name="92213" src=” https://www.ck12.org/flx/show/video/...icity-Overview "thumbnailurl="” title="VideoObject? hash=30acd2f0d8272541c1ce4d3f07362e1a” uploaddate="2016-07-12 20:22:16 "width=” 80% “>

---

El vocabulario

Término	Definición
Completando la Plaza	Completar el cuadrado es un método común para reescribir cuadráticas. Se refiere a hacer un trinomio cuadrado perfecto sumando el cuadrado de 1/2 del coeficiente del término x.
Cónico	Las secciones cónicas son aquellas curvas que se pueden crear por la intersección de un doble cono y un plano. Incluyen círculos, elipses, parábolas e hipérbolas.
Excentricidad	La excentricidad de una sección cónica es una medida de cuánto se desvía la sección cónica de ser circular. La excentricidad de los círculos es 0, la excentricidad de las elipses está entre 0 y 1, la excentricidad de las parábolas es 1, y la excentricidad de las hipérbolas es mayor que 1. Para elipses e hipérbolas,\(\ e=\frac{c}{a}\).
Elipse	Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos.
Elipses	Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos.
Focos	Los focos de una elipse son los dos puntos que definen la elipse. La suma de las distancias desde cualquier punto de la elipse a los focos es constante.
Eje Mayor	El eje mayor de una elipse es el diámetro más largo de la elipse.
eje menor	El eje menor de una elipse es el diámetro más corto de la elipse.
forma estándar	La forma estándar de una elipse centrada en\(\ (h,k)\) es\(\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\).