6.2.3: Parábolas con cualquier vértice
- Page ID
- 108893
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Parábolas con vértice a (h, k)
Tu tarea es encontrar el foco de la parábola\(\ (x+4)^{2}=-12(y-5)\). Dices que el foco es (−4, 5). Banu dice que el foco es (0, −3). Carlos dice que el foco es (−4, 2). ¿Cuál de ustedes es correcto?
Parábolas con vértice a (h, k)
Ya aprendiste que las parábolas no siempre tienen su vértice en (0, 0). En este concepto, abordaremos las parábolas donde está el vértice (h, k), aprenderemos a encontrar el foco, la directrix y la gráfica.
Recordemos que la ecuación de una parábola es\(\ x^{2}=4 p y\) o\(\ y^{2}=4 p x\) y el vértice está en el origen. También, recordemos que la forma de vértice de una parábola es\(\ y=a(x-h)^{2}+k\). Combinando los dos, podemos encontrar la forma de vértice para cónicas.
\ (\\ begin {aligned}
y &=a (x-h) ^ {2} +k\ text {y} x^ {2} =4 p y & &\ text {Resuelve el primero para} (x-h) ^ {2}\\
(x-h) ^ {2} &=\ frac {1} {a} (y-k) &\ text {Encontramos que} 4 p=\ frac {1} {a}\\
(x-h) ^ {2} &=4 p (y-k) & &
\ end { alineado}\)
Si la parábola es horizontal, entonces la ecuación lo será\(\ (y-k)^{2}=4 p(x-h)\). Observe, que aunque se cambie la orientación, los\(\ k\) valores\(\ h\) y permanecen con los\(\ y\) valores\(\ x\) y, respectivamente.
Encontrar el foco y la directrix son un poco más complicados. Utilice la tabla extendida a continuación para ayudarle a encontrar estos valores.
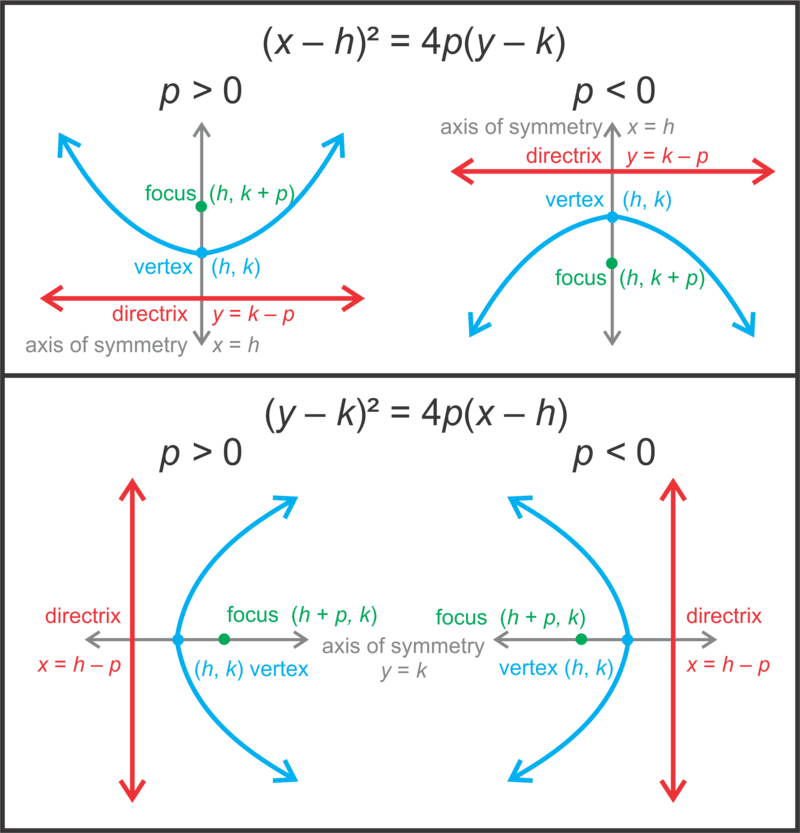
Observe que la forma en que encontramos el foco y la directrix no cambia si\(\ p\) es positiva o negativa.
Analicemos la ecuación\(\ (y-1)^{2}=8(x+3)\). Encontraremos el vértice, el eje de simetría, el enfoque y la directrix. Entonces, determinaremos si la función se abre arriba, abajo, izquierda o derecha.
Primero, porque\(\ y\) es cuadrada, sabemos que la parábola se abrirá a la izquierda o a la derecha. Podemos concluir que la parábola se abrirá a la derecha porque 8 es positivo, es decir, eso\(\ p\) es positivo. A continuación, encuentra el vértice. Usando la ecuación general,\(\ (y-k)^{2}=4 p(x-h)\), el vértice es (−3, 1) y el eje de simetría es\(\ y=1\). \(\ 4 p=8\)Enfrentando, tenemos eso\(\ p=2\). Sumando\(\ p\) al\(\ x\) -valor del vértice, obtenemos el foco, (−1, 1). Restando\(\ p\) del\(\ x\) -valor del vértice, obtenemos la directrix,\(\ x=−5\).
Vamos a graficar la parábola del problema anterior. Trazar el vértice, el eje de simetría, el enfoque y la directrix.
Primero, graficar todos los valores críticos que encontramos anteriormente. Luego, determina un conjunto de puntos simétricos que están en la parábola para asegurarte de que tu curva sea correcta. Si\(\ x=5\), entonces\(\ y\) es -7 o 9. Esto significa que los puntos (5, −7) y (5, 9) están ambos en la parábola.
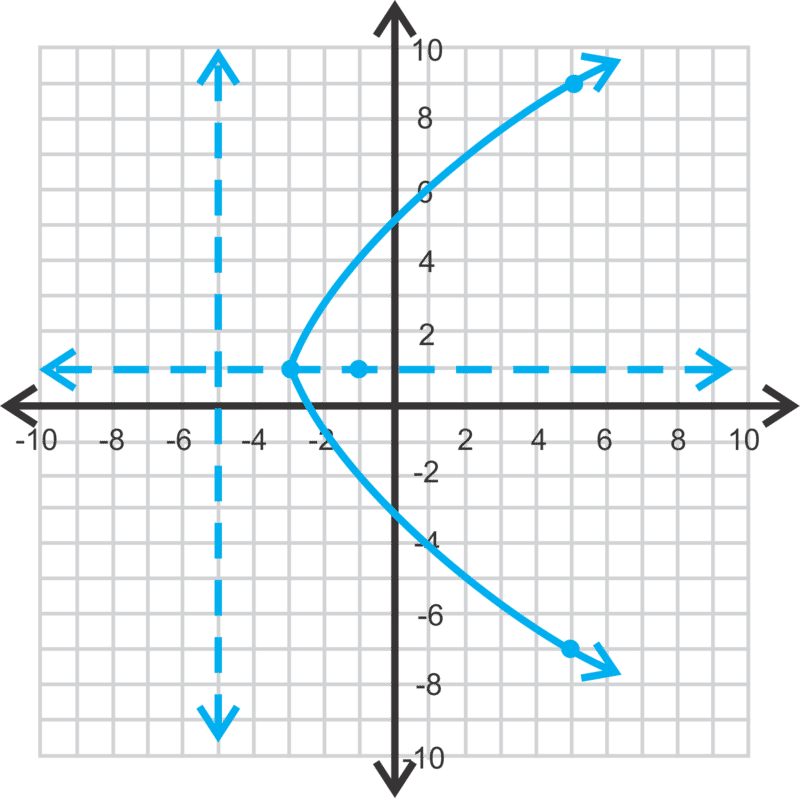
Es importante señalar que las parábolas con orientación horizontal no son funciones porque no pasan la prueba de línea vertical.
El vértice de una parábola es (−2, 4) y la directrix es y=7. Encontremos la ecuación de la parábola.
Primero, determinemos la orientación de esta parábola. Debido a que la directrix es horizontal, sabemos que la parábola se abrirá hacia arriba o hacia abajo (ver tabla/imágenes arriba). También sabemos que la directrix está por encima del vértice, haciendo que la parábola se abra hacia abajo y\(\ p\) será negativa (traza esto en un plano x−y si no está seguro).
Para encontrar\(\ p\), podemos usar el vértice,\(\ (h,k)\) y la ecuación para una directrix horizontal,\(\ y=k−p\).
\ (\\ begin {aligned}
7 &=4-p\\
3 &=-p\ quad\ quad\ quad\ quad\ quad\ text {Recuerda,} p\ text {es negativo debido a la orientación hacia abajo de la parábola.} \\
-3 &=p
\ final {alineado}\)
Ahora, usando la forma general,\(\ (x-h)^{2}=4 p(y-k)\), podemos encontrar la ecuación de esta parábola.
\ (\\ comenzar {alineado}
(x- (-2)) ^ {2} &=4 (-3) (y-4)\\
(x+2) ^ {2} &=-12 (y-4)
\ final {alineado}\)
Ejemplos
Anteriormente, se le pidió que determinara qué estudiante es correcto.
Solución
Esta parábola es de la forma\(\ (x-h)^{2}=4 p(y-k)\). De la mesa anterior en esta lección, podemos ver que el foco de una parábola de esta forma es\(\ (h, k+p)\). Entonces ahora tenemos que encontrar h, k, y p.
Si comparamos\(\ (x+4)^{2}=-12(y-5)\) con\(\ (x-h)^{2}=4 p(y-k)\), vemos que:
- \(\ 4=-h \text { or } h=-4\)
- \(\ -12=4 p \text { or } p=-3\)
- \(\ 5=k\)
De estos hechos podemos encontrar\(\ k+p=5+(-3)=2\).
Por lo tanto, el foco de la parábola es\(\ (−4,2)\) y Carlos es correcto.
Encuentra el vértice, foco, eje de simetría y directrix de\(\ (x+5)^{2}=2(y+2)\).
Solución
El vértice es\(\ (-5,-2)\) y la parábola se abre porque\(\ p\) es positiva y\(\ x\) está cuadrada.
\(\ 4 p=2\), haciendo\(\ p=\frac{1}{2}\). El foco es\(\ (-5,-2+2)\) o\(\ (-5,0)\), el eje de simetría es\(\ x=-5\), y la directrix es\(\ y=-2-\frac{1}{2}\) o\(\ y=-2 \frac{1}{2}\).
Grafica la parábola del Ejemplo 2.
Solución
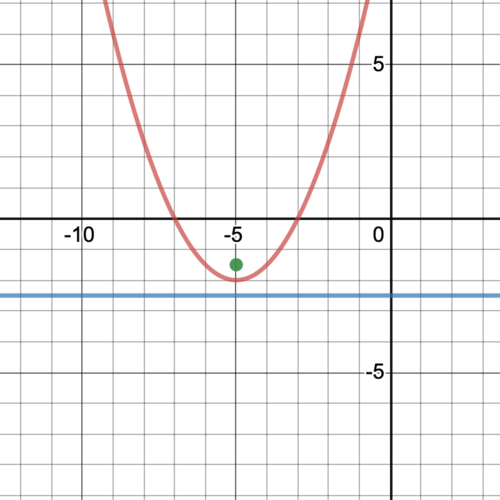
Encuentra la ecuación de la parábola con vértice (−5, −1) y foco (−8, −1).
Solución
El vértice es (−5, −1), así\(\ h=−5\) y\(\ k=−1\). El foco es (−8, −1), lo que significa que esa parábola será horizontal. Esto lo sabemos porque los valores y del vértice y el foco son ambos -1. Por lo tanto,\(\ p\) se suma o resta a\(\ h\).
\(\ (h+p, k) \rightarrow(-8,-1)\)podemos inferir eso\(\ h+p=-8 \rightarrow-5+p=-8\) y\(\ p=-3\)
Por lo tanto, la ecuación es\(\ (y-(-1))^{2}=4(-3)(x-(-5)) \rightarrow(y+1)^{2}=-12(x+5)\)
Revisar
Encuentra el vértice, foco, eje de simetría y directrix de las parábolas a continuación.
- \(\ (x+1)^{2}=-3(y-6)\)
- \(\ (x-3)^{2}=y-7\)
- \(\ (y+2)^{2}=8(x+1)\)
- \(\ y^{2}=-10(x-3)\)
- \(\ (x+6)^{2}=4(y+8)\)
- \(\ (y-5)^{2}=-\frac{1}{2} x\)
- Grafica la parábola de #1.
- Grafica la parábola de #2.
- Grafica la parábola de #4.
- Grafica la parábola de #5.
Encuentra la ecuación de la parábola dado el vértice y ya sea el foco o directrix.
- vértice: (2, −1), enfoque: (2, −4)
- vértice: (−3, 6), directrix: x = 2
- vértice: (6, 10), directrix: y = 9.5
- Enfoque de desafío: (−1, −2), directrix: x = 3
- Extensión Reescribe la ecuación de la parábola, x 2 − 8x + 2y + 22 = 0, en forma estándar completando el cuadrado. Entonces, encuentra el vértice.
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.2.
El vocabulario
| Término | Definición |
|---|---|
| Forma de vértice | La forma de vértice de una parábola es\(\ (x-h)^{2}=4 p(y-k)\) o\(\ (y-k)^{2}=4 p(x-h)\) dónde\(\ (h,k)\) está el vértice. |
Atribuciones de imagen
- [Figura 1]
Crédito: Holly Fischer
Fuente: https://commons.wikimedia.org/wiki/File:Three_Main_Layers_of_the_Eye.png

