6.2.5: Aplicaciones de Parabolas
- Page ID
- 108874
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aplicaciones de Parábolas
Kelly está casi terminada con el capítulo sobre parábolas en su clase de matemáticas. Se ha familiarizado bastante con la forma general de una parábola, y ha comenzado a notar el uso de parábolas a su alrededor. Una cosa que aún no ha descubierto es por qué los platos de televisión por satélite son parábolas 3D. Ella está segura que no es una coincidencia, pero no sabe de qué se trata una forma parabólica que es importante.
¿Sabes?
Aplicaciones de Parábolas
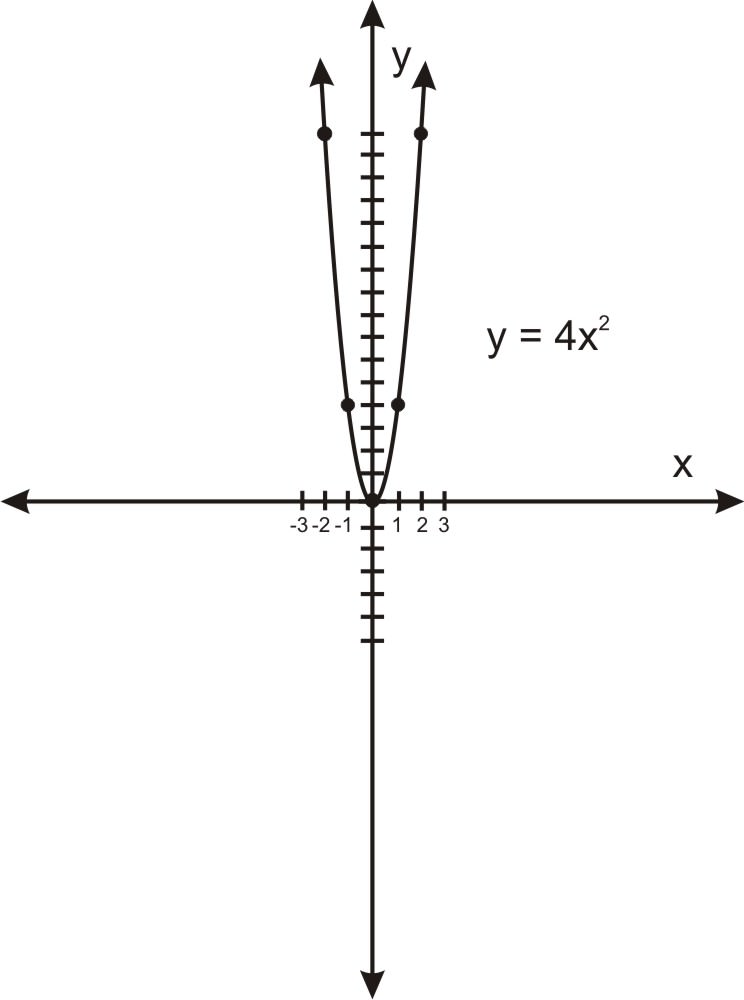
Hay una propiedad muy interesante de parábolas. Este es el hecho de que todas las parábolas tienen la misma forma. O, en el lenguaje de la geometría, dos parábolas cualesquiera son similares entre sí. Esto significa que cualquier parábola se puede escalar dentro o fuera para producir otra parábola exactamente de la misma forma. Esto puede parecer sorprendente, porque las parábolas donde\(\ x^{2}\) tiene un coeficiente grande ciertamente se ven mucho más “empinadas” que las parábolas con un coeficiente pequeño cuando se examinan sobre el mismo dominio, como se muestra en las gráficas a continuación.
|
a. Alto y flaco:
|
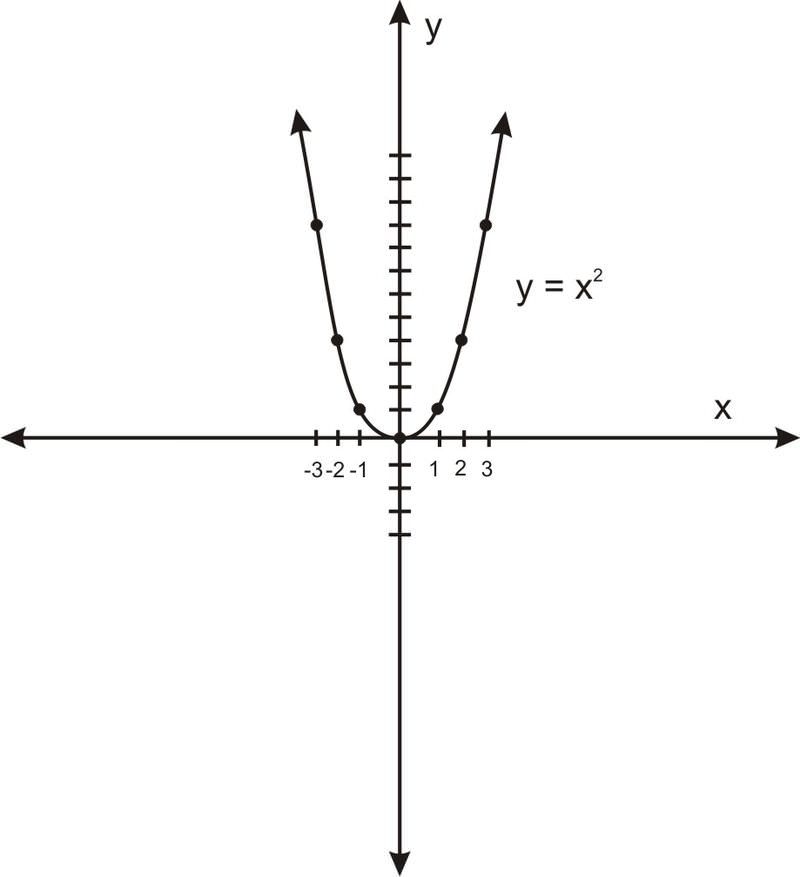
b. corto y ancho:
|
|---|
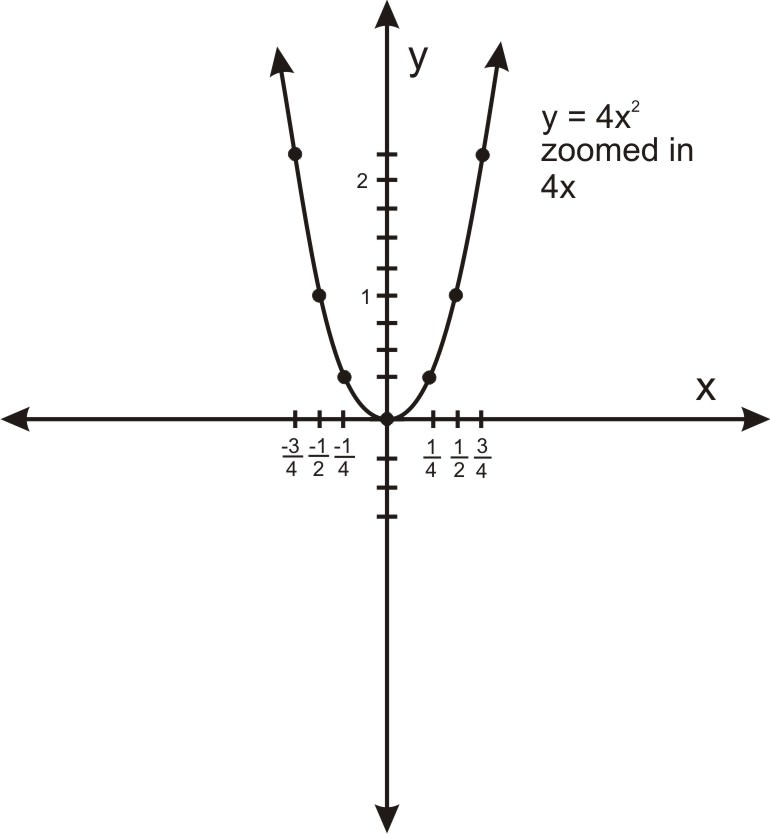
Pero cuando una de las parábolas se escala apropiadamente, estas parábolas son idénticas:
|
a. Alto y flaco - ampliada 4x:
|
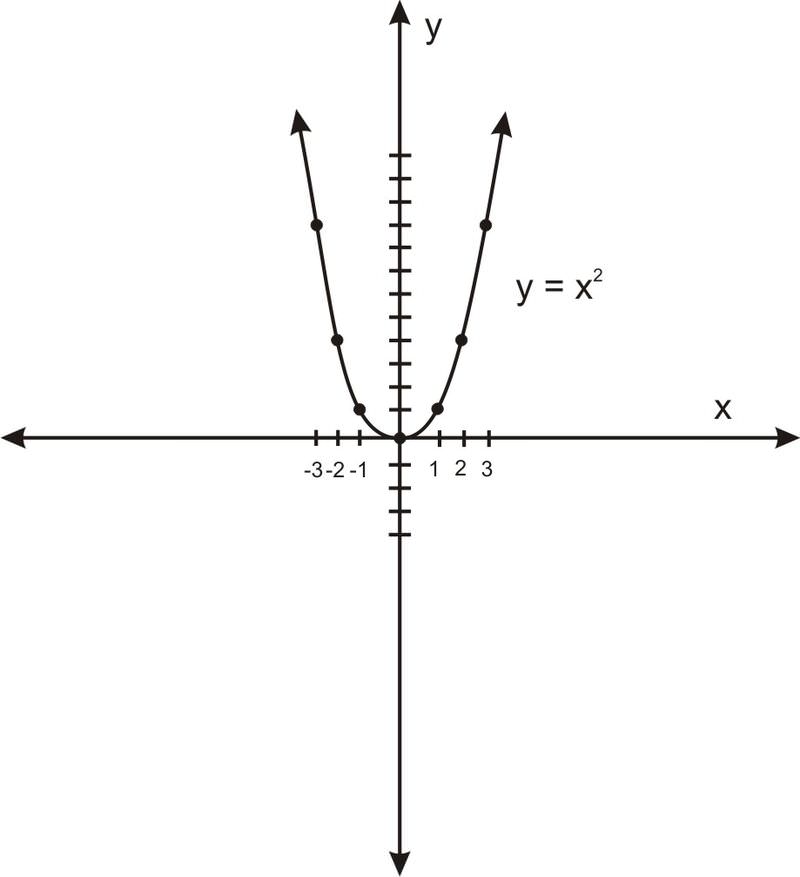
b. corto y ancho:
|
|---|
Este dato sobre las parábolas se puede ver desde el punto de vista álgebra dado que todas las parábolas se generan a partir de una línea y un punto no en esa línea. Esta configuración de generar objetos, una línea y un punto, es siempre la misma forma. Cualquier otra línea y punto se ve exactamente igual, simplemente acercar o alejar hasta que la línea y el punto estén a la misma distancia entre sí. Por lo que las formas que cualquiera de tales configuraciones generan también deben ser la misma forma.
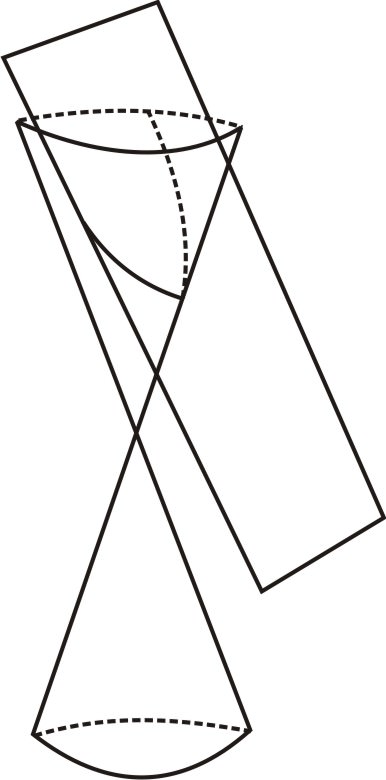
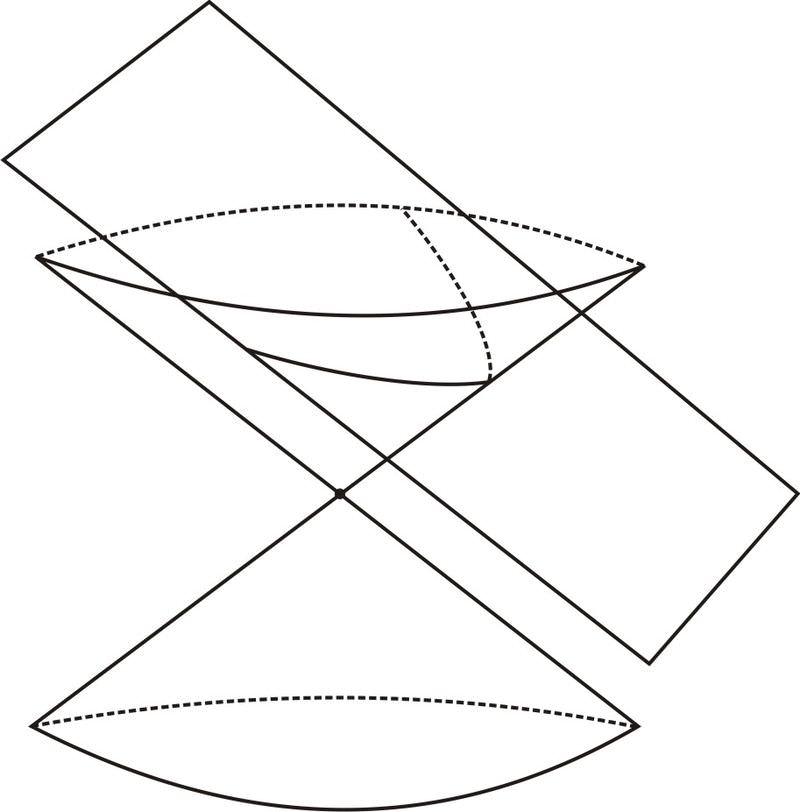
Desde el punto de vista de la geometría analítica, hubo dos factores que podrían afectar la forma de la parábola. El primero es la distancia entre el plano de corte y el vértice del cono. Pero los conos tienen las mismas proporciones a cualquier escala, así que no importa cuál sea esta distancia, la imagen se puede reducir o agrandar, afectando esta distancia pero no la forma del cono o plano. Entonces este parámetro en realidad no cambia la forma de la sección cónica que resulta. El otro factor es la forma del cono real. Esta es su inclinación, definida por el ángulo en el vértice, o equivalentemente por la relación entre el radio y la altura en cualquier punto. Esto es un poco más complicado. No es para nada obvio que los conos cortos, en cuclillas y los conos altos y delgados producirían parábolas de la misma forma.
|
a. Alto y flaco:
|
b. corto y ancho:
|
|---|
Según lo que encontramos, cualquier parábola producida por rebanar cualquier cono resultó en una ecuación de esta forma:
\(\ y=a x^{2}\)
Queremos demostrar que si generamos dos de esas parábolas, que en realidad tienen la misma forma. Entonces supongamos que usamos dos construcciones de cono y se nos ocurren estas parábolas:
\(\ y=a_{1} x^{2}\)y\(\ y=a_{2} x^{2}\). Queremos mostrar que hay algún factor de escala, llámalo\(\ f\), que se encoge o se agranda\(\ y=a_{1} x^{2}\) en\(\ y=a_{2} x^{2}\). Para mantener una forma igual, el factor de escala necesita afectar tanto al\(\ x-\) como\(\ y-\text { variables }\). Entonces necesitamos encontrar un\(\ f\) tal que\(\ (f y)=a_{1}(f x)^{2}\) sea equivalente a\(\ y=a_{2} x^{2}\). Se puede escribir la primera ecuación\(\ y=\left(a_{1} f\right) x^{2}\), lo que equivale a la segunda ecuación cuándo\(\ a_{1} f=a_{2}\), o cuándo\(\ f=\frac{a_{2}}{a_{1}}\). Tal\(\ f\) siempre existe para números no negativos\(\ a_{1}\) y\(\ a_{2}\). Entonces las parábolas son de hecho la misma forma. Si\(\ a\) es menor que cero, entonces la parábola puede reflejarse verticalmente para producir una parábola de la misma forma y con coeficiente positivo\(\ a\).
Aplicaciones de parábola
Espejos Burning
Diócles (~240−180 a. C.) fue un matemático de la Antigua Grecia del que sabemos muy poco. No obstante, sabemos lo suficiente por unos pocos documentos escasos que pensó en una importante aplicación de las parábolas. Proviene de lo que a veces se llama la “propiedad óptica” de las parábolas. Recuerda la propiedad óptica de las elipses: las líneas de un foco “rebotan” en el lado de la elipse para golpear el otro foco.
Para las parábolas, ya que las parábolas tienen un solo enfoque, la directrix juega un papel importante. Para la parábola, la propiedad óptica es que las líneas perpendiculares a la directriz “rebotan” en la parábola y convergen en el foco. O, alternativamente, las líneas del foco “rebotan” en la parábola y continúan perpendiculares a la directriz. Al igual que con la elipse, “rebotar” significa que las dos líneas se encuentran con la parábola en ángulos iguales a la tangente.
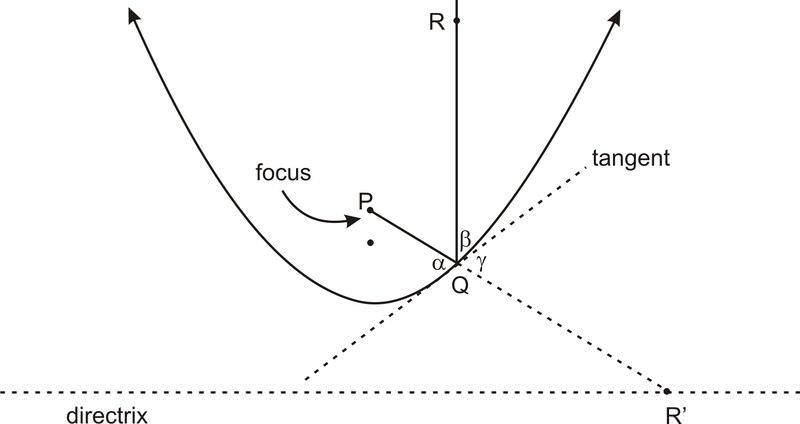
En el diagrama anterior, la propiedad óptica establece que ◻ α◻ β. La prueba es similar a la prueba de la propiedad óptica de las elipses. En el diagrama anterior P es el foco y Q es un punto en la parábola. Sea R′ el punto en la directriz que se obtiene extendiendo PQ. Entonces PR′, la línea recta, es claramente la distancia más corta entre P y R′ que pasa por la línea tangente. Que R esté en la línea que se encuentra directamente por encima de Q de tal manera que QR=QR′. La R puede ser pensada como R′, reflejada a través de la línea tangente. Entonces ◻ α◻ γ (ángulos verticales) y ◻ γ◻ β (ángulos reflejados), y así ◻ α◻ β (propiedad transitiva).
La propiedad óptica tiene algunas aplicaciones interesantes. Diocles describió una posible aplicación en su documento “On Burning Mirrors”. Imaginó un espejo con forma parabólica (básicamente una parábola girada alrededor de su línea de simetría) que recogería la luz del sol y la enfocaría en el punto focal, creando suficiente concentración de luz para iniciar un incendio en ese punto. Algunos afirman que Arquímedes intentó hacer tal artilugio con placas de cobre para luchar contra los romanos en Siracusa.
|
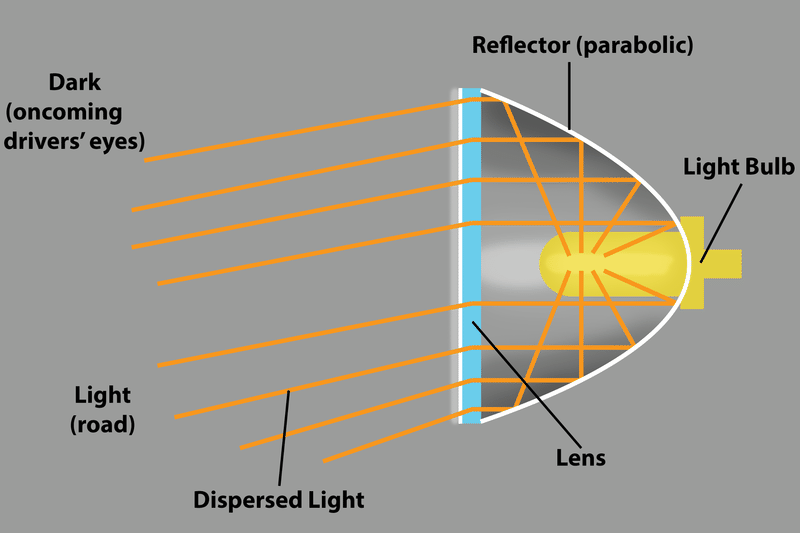
Faros: La propiedad óptica también es responsable de las luces unidireccionales en forma de parabola, como los faros de los automóviles. Si se coloca una bombilla en el foco de un espejo parabólico, los rayos de luz se reflejan en el espejo paralelos entre sí, haciendo un haz de luz enfocado.
|
Telescopios Cassegrain: Los telescopios satelitales aprovechan la propiedad óptica de las parábolas para recolectar la mayor cantidad de luz de una estrella distante como sea posible. El plato del satélite de abajo es de forma parabólica y refleja la luz hasta el punto en el medio.
|
|---|
Ejemplos
Anteriormente, se le hizo una pregunta sobre por qué los platos de televisión por satélite son parábolas 3D.
Solución
La antena parabólica es una parábola 3D por lo que toda la señal que recoge en un área amplia se concentrará en el foco de la parábola, aumentando significativamente la recepción.
Explica por qué no todas las elipses son similares como son las parábolas. Si bien ampliar o reducir no funciona para hacer dos elipses idénticas, ¿cómo se puede cambiar la vista de dos elipses que tienen formas diferentes para que se vean iguales?
Solución
La excentricidad de las elipses define la forma, por lo que cuando la excentricidad es diferente para dos elipses, las elipses no son similares entre sí. Al ver una de las elipses en ángulo, sin embargo, cambia la excentricidad percibida de esa elipse, y el ángulo puede elegirse para que coincida con la excentricidad percibida con la excentricidad de la otra elipse, produciendo una imagen similar a la otra elipse.
Si no se usaba nada para desviar la luz antes de que entrara en un "espejo ardiente”, ¿dónde tendría que estar el sol en relación contigo y con el lugar donde quieres iniciar un incendio? ¿Por qué es esto una restricción? Diseñar una manera de eludir esta restricción.
Solución
El lugar de fuego debe estar en el segmento entre usted y el sol. Esto es un problema porque para iniciar un incendio terrestre, tendrías que esperar hasta la tarde cuando el sol está bajo en el cielo para poder apuntar tu lente al suelo, desafortunadamente el sol no es tan brillante en la tarde por lo que perderías una cantidad significativa de potencia. Una lente o espejo que cambie el ángulo de los rayos solares podría ayudarte a evitar esta restricción.
En el diagrama anterior de un faro de automóvil, la lente dirige los haces de luz hacia abajo, para mantenerlos fuera de los ojos de los conductores que se aproximan, si ese era el único propósito de la lente, alternativamente la lente podría omitirse y el faro podría simplemente inclinarse ligeramente hacia abajo. Pero hay otro propósito en la lente. ¿Qué es?
Solución
La lente también expande la matriz de luz, razón por la cual se llama “luz dispersa”. Sin la lente, el faro sólo iluminaría una tira del ancho del faro mismo, lo que no sería muy útil para conducir.
Una antena parabólica debe construirse en forma de paraboloide. El paraboloide se forma girando la parábola con foco en el punto (25, 0) y directriz\(\ x=−25\) alrededor del eje x, donde x e y están en pulgadas. El diámetro de la antena debe ser de 80 pulgadas.
- Encuentra la ecuación de la parábola y el dominio de x.
- Esboza la gráfica de la parábola, mostrando la ubicación del foco.
- Un receptor se va a colocar en el foco. El diseñador ha advertido que un usuario o instalador debe tener cuidado, el receptor golpearía el suelo y podría dañarse si la antena se colocara “boca abajo”. Determinar algebraicamente si esta observación es correcta.
Solución
- \(\ x=\frac{1}{100} y^{2}\)
El dominio es el conjunto de números reales positivos.
- Esboza la gráfica de la parábola, mostrando la ubicación del foco.
- Sí, como se descubrió en la parte a y se muestra en la gráfica de la parte b, el foco está en x = 25, mientras que el platillo sólo se extiende a x = 16.
Revisar
- fútbol con una velocidad vertical inicial de 96 pies por segundo. ¿Después de cuántos segundos alcanzará la pelota su máxima altura sobre el nivel del mar? ¿Cuál es la altura máxima?
- Una pistola de disparo se descarga verticalmente hacia arriba a una altura de 3 pies sobre el suelo. Si la bala tiene una velocidad inicial del hocico de 200 pies por segundo, ¿qué altura máxima alcanzará antes de que empiece a caer al suelo? a) 628 pies b) 1,878 pies c) 20.87 pies d) 199.33 pies
- Un golfista demasiado celoso golpea un tiro de flop con una cuña de arena para salir de la esquina de un viaje de arena con una velocidad vertical inicial de 45 pies por segundo. ¿Cuál es la altura máxima que alcanzará la pelota de golf? a) 45 pies b) 13.19 pies c) 36.64 pies d) 95,26 pies
- Estás parado en la cima de una colina de 1680 pies de altura y lanzas una pequeña pelota hacia arriba. A cada segundo, se mide la distancia de la pelota desde el suelo. Exactamente t segundos después de lanzar el objeto, su altura, (medida en pies) es\(\ h(t)=-16 t^{2}+256 t+1680\) a) Encuentra\(\ h(3)\) la posición de la pelota 3 segundos después de lanzarlo. b) ¿Cuánto viaja el objeto durante los dos segundos entre 5 segundos y 7 segundos? c) ¿Cuánto tiempo tarda el objeto en alcanzar una altura de 2640 pies? d) ¿Cuánto tiempo tarda el objeto en golpear el suelo?
- Un estudiante que participaba en un juego de kick ball pateó la pelota con una velocidad vertical inicial de 32 pies por segundo. Su altura sobre la tierra en pies viene dada por\(\ s(t)=-16 t^{2}+32 t\) donde t es el tiempo en segundos. ¿Cuál es la altura máxima que alcanza el balón? SUGERENCIA - Grafica la parábola (solo necesitas preocuparte por la sección donde 0≤t≤2 o reescribir la ecuación para encontrar el vértice.
- Un arco sobre la entrada a un sendero encantado tiene forma parabólica, el arco tiene una altura de 25 pies y está a 30 pies entre los pilares de soporte. Encuentra una ecuación que modele el arco, usando el eje x para representar el suelo del parque. Declarar el foco y directriz.
- Una antena parabólica tiene forma parabólica con un diámetro de 80 metros. Las señales de tv recolectadas se enfocan en un solo punto, llamado el punto “focal”, que es el foco del paraboloide (la sección transversal de la parábola). Si la distancia focal es de 45 metros, encuentra la profundidad del platillo, redondeada a un decimal.
- Cuando entran nuevas autopistas, a menudo están diseñadas con superficies parabólicas que permiten drenar el agua. Se está colocando una nueva carretera, tiene 32 pies de ancho y es de .4 pies más alta en el centro de la carretera luego en los lados. a) Encuentra una ecuación si la parábola que modela la superficie de la carretera (supongamos que el origen está en el centro de la autopista) b) Qué tan lejos del centro de la carretera está la superficie de la carretera .1 pies más bajos que en el medio?
- La distancia interna del boceto de un arco es de 8cm y la altura del arco es de 9cm. Suponiendo la escala 1cm = 2m, elaborar una fórmula que calcule la altura real del borde interior de esta estructura (y), en metros a cualquier distancia horizontal x medida desde el punto de origen que es el piso en el centro del arco.
Se ha construido un nuevo puente para el tránsito peatonal a través de un río. Las dos torres en cada extremo del puente tienen 50 pies de altura y 300 pies una de la otra. Los cables de soporte (2) están conectados en la parte superior de las torres y cuelgan en una curva que forma la forma de una parábola. Hay cables verticales que conectan la pasarela a los cables de soporte. Estos cables se conectan cada 15 pies desde la pasarela hasta los cables de soporte. En el centro del puente, la parábola se encuentra a 5 pies sobre la pasarela.
Specialty Cable Company back east vende cable por $52.75 por 10 pies con un cargo de envío de $300.00 para todo el pedido. Cables R US, en la costa oeste vende cable por $432.90 por 100 pies con un cargo de envío de $350.00 para todo el pedido. El cable tuvo que comprarse en longitudes de 10 pies de SCC o en longitudes de 100 pies de CRUS. Una vez comprados, los cables se pueden cortar o soldar juntos.
- Escribe una ecuación para la parábola que represente cada uno de los cables de soporte.
- Determine el número de cables verticales necesarios.
- Determinar la longitud de cada uno de los cables verticales.
- ¿Cuánto cuesta comprar los materiales necesarios a cada empresa?
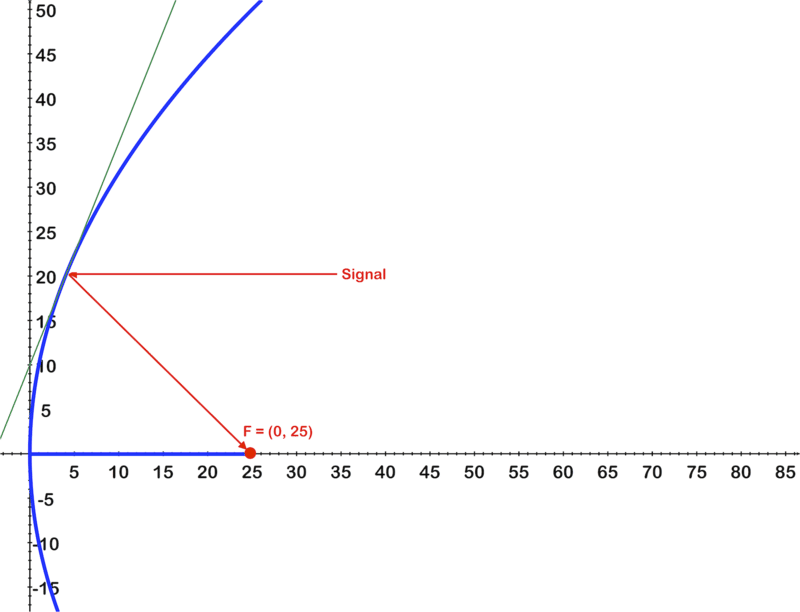
Mira la imagen. Muestra la sección transversal parabólica de una antena parabólica. La ecuación para la parábola es\(\ x=0.01 y^{2}\)

- ¿Cuál es el foco de la parábola como se muestra en la imagen?
- Una señal de radio viene en y = 20 como se marca en rojo. Identificar donde el rayo golpea la parábola, da coordenadas.
- Identificar la medida del ángulo entre el rayo entrante y una línea entre el punto de ataque y el foco.
- Un rayo entrante y su rayo reflejado forman ángulos de igual medida con una línea tangente a la superficie curva. Usa el ángulo que acabas de medir entre la señal y la línea reflejada para calcular las medidas de los ángulos entre la señal entrante y la tangente al punto de impacto y de la tangente al rayo reflejado. ¿Son lo mismo? Mida con un prolongador para confirmar sus cálculos.
- Encuentra la ecuación para la línea tangente. Usa el ángulo C para encontrar su pendiente.
- Elige al azar otro rayo entrante. Calcular los ángulos como antes. ¿El rayo entrante es tangente a la parábola en el punto donde el rayo entrante golpea la gráfica? ¿Cómo lo sabes?
- ¿Qué se puede decir sobre la dirección que toma un rayo reflejado cada vez que el rayo entrante es paralelo al eje de la parábola? ¿Puedes ver por qué se usa el nombre “focus” y por qué las antenas de televisión por satélite y otros dispositivos de escucha están hechos en forma de paraboloide?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.5.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| espejo ardiente | El espejo ardiente es un plato parabólico altamente reflectante que se utiliza para enfocar la luz solar en un solo punto, el foco de la parábola. |
| Elipse | Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos. |
| Elipses | Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos. |
| Parábola | Una parábola es el conjunto de puntos que son equidistantes de un punto fijo en el interior de la curva, llamado el “'foco"', y una línea en el exterior, llamada la “'directrix"'. La directriz es vertical u horizontal, dependiendo de la orientación de la parábola. |
| plato parabólico | Un plato parabólico es una superficie generada por una parábola que gira alrededor de su eje de simetría. |
| Unidireccional | Unidireccional significa enfocarse en una dirección (uni-) específica. |