6.3.3: Hipérbolas con cualquier Centro

Última actualización

30 oct 2022
Guardar como PDF
- 6.3.2: Ecuaciones de Hipérbolas Centradas en los Orígenes
- 6.3.4: Ecuaciones de hipérbola y la propiedad focal

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Hipérbolas Centradas en (h, k)

Tu tarea es graficar la hipérbola $\ 9(y+2)^{2}-4(x-3)^{2}=36$ . ¿Cuáles son los vértices de tu gráfica?

Hipérbolas Centradas en (h, k)

Al igual que has aprendido anteriormente, una hipérbola no siempre tiene que colocarse con su centro en el origen. Si el centro es toda $\ (h,k)$ la elipse se desplazarán $\ h$ las unidades hacia la izquierda o derecha y $\ k$ las unidades hacia arriba o hacia abajo. La ecuación se convierte $\ \frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1$ . Abordaremos cómo cambian los vértices, co-vértices y focos en el siguiente problema.

Vamos a graficar $\ \frac{(x-2)^{2}}{16}-\frac{(y+1)^{2}}{9}=1$ . Entonces, encontremos los vértices, focos y asíntotas.

Primero, sabemos que se trata de una hipérbola horizontal porque el $\ x$ término es primero. Por lo tanto, el centro es $\ (2,−1)$ y $\ a=4$ y $\ b=3$ . Usa esta información para graficar la hipérbola.

Para graficar, trazar el centro y luego salir 4 unidades a la derecha e izquierda y luego arriba y abajo 3 unidades. Dibuja la caja y las asíntotas.

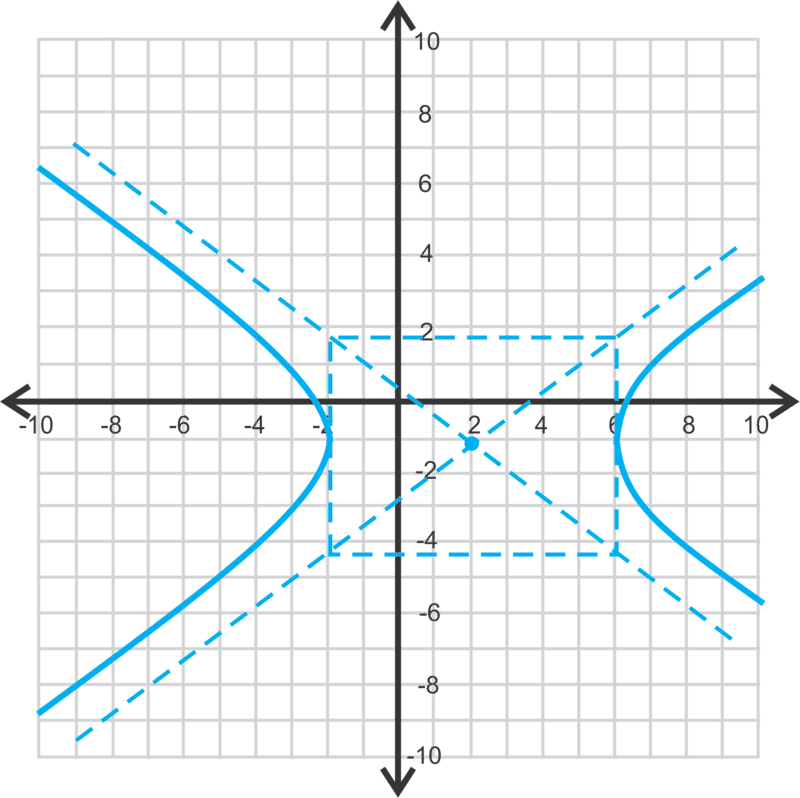
f-d_06127d7eca98afda5ee8a62ee90ee61e84293cfbb33252ba01ee67ce+image_tiny+image_tiny.png

Así es también como puedes encontrar los vértices. Los vértices son $\ (2 \pm 4,-1)$ o $\ (6,-1)$ y $\ (-2,-1)$ .

Para encontrar los focos, necesitamos encontrar el $\ c$ uso $\ c^{2}=a^{2}+b^{2}$ .

\ (\\ begin {array} {l}
c^ {2} &=16+9=25\\
c&=5
\ end {array}\)

Por lo tanto, los focos son $\ (2 \pm 5,-1)$ o $\ (7,−1)$ y $\ (−3,−1)$ .

Para encontrar las asíntotas, tenemos que hacer un poco de trabajo para encontrar las intercepciones y. Sabemos que la pendiente es $\ \pm \frac{b}{a}$ o $\ \pm \frac{3}{4}$ y pasan por el centro. Escribamos cada asíntota en forma de punto- pendiente usando el centro y cada pendiente.

$\ y-1=\frac{3}{4}(x+2)$ y $\ y-1=-\frac{3}{4}(x+2)$

Simplificando cada ecuación, las asíntotas son $\ y=\frac{3}{4} x-\frac{5}{2}$ y $\ y=-\frac{3}{4} x+\frac{1}{2}$ .

A partir de este problema, podemos crear fórmulas para encontrar los vértices, focos y asíntotas de una hipérbola con centro $\ (h,k)$ . Además, al graficar una hipérbola, no centrada en el origen, asegúrate de trazar el centro.

Orientación	Ecuación	Vértices	Focos	Asíntotas
Horizontal	$\ \frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1$	$\ (h \pm a, k)$	$\ (h \pm c, k)$	$\ y-k=\pm \frac{b}{a}(x-h)$
Vertical	$\ \frac{(y-k)^{2}}{a^{2}}+\frac{(x-h)^{2}}{b^{2}}=1$	$\ (h, k \pm a)$	$\ (h, k \pm c)$	$\ y-k=\pm \frac{a}{b}(x-h)$

Ahora, encontremos la ecuación de la hipérbola con vértices $\ (−3,2)$ y $\ (7,2)$ y enfoque $\ (−5,2)$ .

Estos dos vértices crean un eje transversal horizontal, haciendo que la hipérbola sea horizontal. Si no está seguro, trazar la información dada en un conjunto de ejes. Para encontrar el centro, usa la fórmula de punto medio con los vértices.

$\ \left(\frac{-3+7}{2}, \frac{2+2}{2}\right)=\left(\frac{4}{2}, \frac{4}{2}\right)=(2,2)$

La distancia de uno de los vértices al centro es $\ a,|7-2|=5$ . La distancia desde el centro hasta el foco dado es $\ c,|-5-2|=7$ . Usar $\ a$ y $\ c$ resolver para $\ b$ .

\ (\\ begin {array} {l}
7^ {2} =5^ {2} +b^ {2}\\
b^ {2} =24\ fila derecha b=2\ sqrt {6}
\ end {array}\)

Por lo tanto, la ecuación es $\ \frac{(x-2)^{2}}{25}-\frac{(y-2)^{2}}{24}=1$ .

Por último, graficemos $\ 49(y-3)^{2}-25(x+4)^{2}=1225$ y encontremos los focos.

Primero tenemos que poner la ecuación en forma estándar, como las ecuaciones anteriores. Para hacer el lado derecho 1, necesitamos dividir todo por 1225.

\ (\\ begin {array} {c}
\ frac {49 (y-3) ^ {2}} {1225} -\ frac {25 (x+4) ^ {2}} {1225} =\ frac {1225} {1225}\
\ frac {(y-3) ^ {2}} {25} -\ frac {(x+4) ^ {2}} {49} =1
\ end {array}\)

Ahora bien, sabemos que la hipérbola será vertical porque el término y es primero.

$\ a=5$ , $\ b=7$ y el centro es $\ (−4,3)$ .

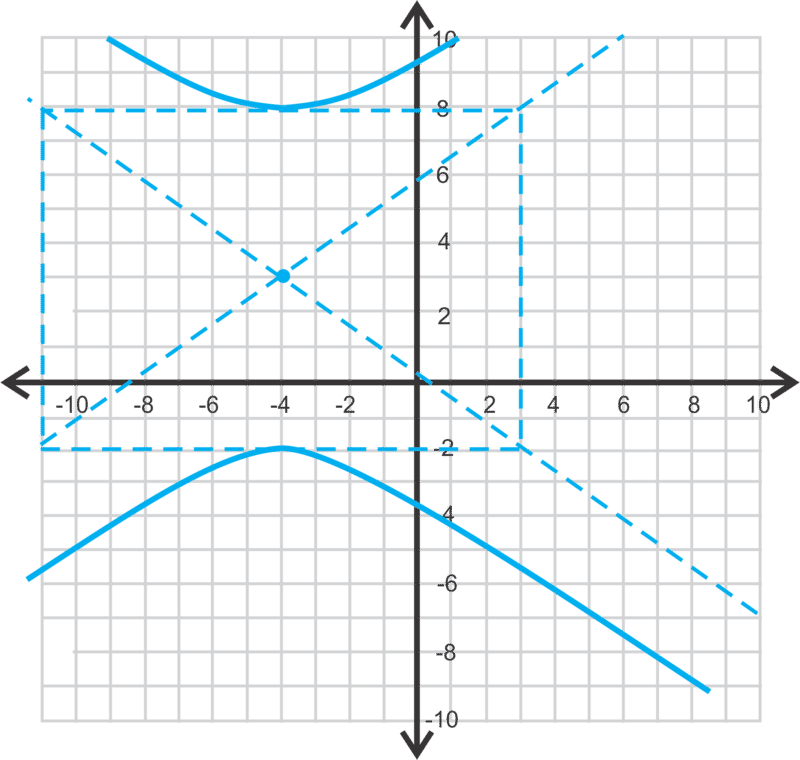
f-d_2eae7a95a3ac69913e98a60915df1e2a616362b160bb436e679a2a30+image_tiny+image_tiny.png

Para encontrar los focos, primero necesitamos encontrar $\ c$ usando $\ c^{2}=a^{2}+b^{2}$ .

\ (\\ comenzar {alineado}
c^ {2} &=49+25=74\\
c &=\ sqrt {74}
\ end {alineado}\)

Los focos son $\ (-4,3 \pm \sqrt{74})$ o $\ (−4,11.6)$ y $\ (−4,−5.6)$ .

Ejemplos

Ejemplo 1

Anteriormente, se le pidió que identificara los vértices de la gráfica de la hipérbola definida por $\ 9(y+2)^{2}-4(x-3)^{2}=36$ .

Solución

Primero necesitamos obtener la ecuación en forma estándar $\ \frac{(y-k)^{2}}{a^{2}}+\frac{(x-h)^{2}}{b^{2}}=1$ , así dividimos por $\ 36$ .

\ (\\ begin {array} {r}
9 (y+2) ^ {2} -4 (x-3) ^ {2} =&36\\
\ frac {9 (y+2) ^ {2}} {36} -\ frac {4 (x-3) ^ {2}} {36} =&\ frac {36} {36}\
\ frac {(y+2) ^ {2}} {4} -\ frac {(x-3) ^ {2}} {9} =&1
\ end {array}\)

Debido a que el término y es primero, ahora podemos ver que los vértices son $\ (h, k \pm a)(3,-2 \pm 2)$ . Es decir, $\ (3,0)$ y $\ (3,−4)$

Ejemplo 2

Encuentra el centro, vértices, focos, y asíntotas de $\ \frac{(y-1)^{2}}{81}-\frac{(x+5)^{2}}{16}=1$ .

Solución

El centro es $\ (−5,1)$ , $\ a=\sqrt{81}=9$ y $\ b=\sqrt{16}=4$ , y la hipérbola es horizontal porque el término y es primero. Los vértices son $\ (-5,1 \pm 9)$ o $\ (-5,10)$ y $\ (−5,−8)$ . $\ c^{2}=a^{2}+b^{2}$ Úselo para encontrar $\ c$ .

\ (\\ comenzar {alineado}
c^ {2} &=81+16=97\\
c &=\ sqrt {97}
\ end {alineado}\)

Los focos son $\ (-5,1+\sqrt{97})$ y $\ (-5,1-\sqrt{97})$ .

Las asíntotas son $\ y-1=\pm \frac{9}{4}(x+5)$ o $\ y=\frac{9}{4} x+12 \frac{1}{4}$ y $\ y=-\frac{9}{4} x-10 \frac{1}{4}$ .

Ejemplo 3

Grafica $\ 25(x-3)^{2}-4(y-1)^{2}=100$ y encuentra los focos.

Solución

Cambia esta ecuación a forma estándar para poder graficar.

\ (\\ begin {array} {l}
\ frac {25 (x-3) ^ {2}} {100} -\ frac {4 (y-1) ^ {2}} {100} &=\ frac {100} {100}\
\ frac {(x-3) ^ {2}} {4} -\ frac {(y-1) ^ {2}} {25} &=1
\ end {array}\)

centro: $\ (3,1), a=2, b=5$

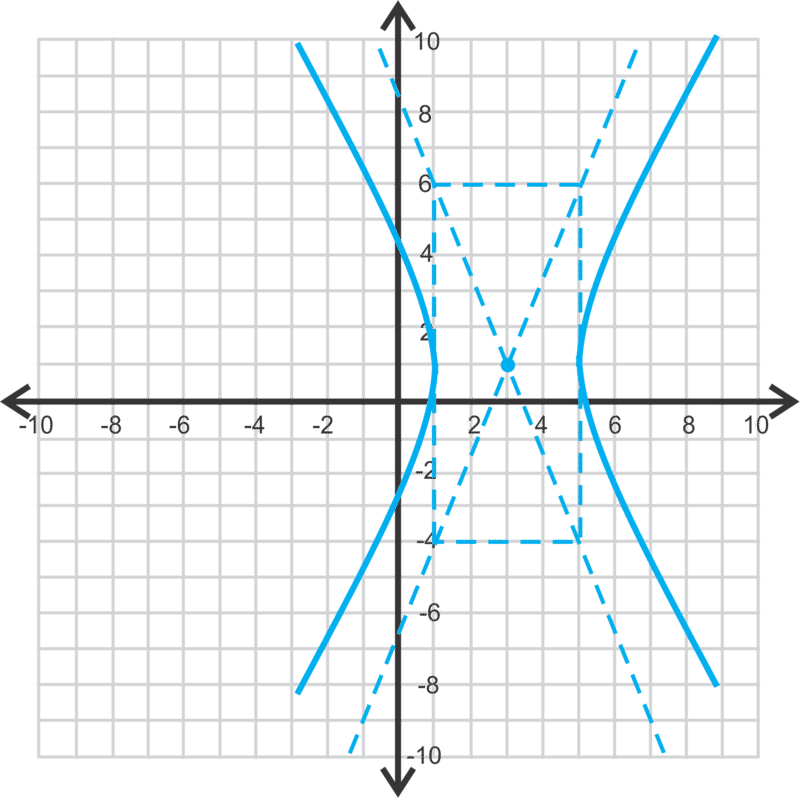
f-d_ccc6d9d6261c5586c55c80a6e035bcbbe3e0470159203c5bb62ca61e+image_tiny+image_tiny.png

Encuentra los focos.

\ (\\ begin {array} {l}
c^ {2} &=25+4=29\\
c&=\ sqrt {29}
\ end {array}\)

Los focos son $\ (3,1+\sqrt{29})$ y $\ (3,1-\sqrt{29})$ .

Ejemplo 4

Encuentra la ecuación de la hipérbola con vértices $\ (−6,−3)$ y $\ (−6,5)$ y enfoque $\ (−6,7)$ .

Solución

Los vértices son $\ (−6,−3)$ y $\ (−6,5)$ y el foco es $\ (−6,7)$ . El eje transversal va a ser vertical porque el valor x no cambia entre estos tres puntos. La distancia entre los vértices es $\ |-3-5|=8$ unidades, haciendo $\ a=4$ . El punto medio entre los vértices es el centro.

$\ \left(-6, \frac{-3+5}{2}\right)=\left(-6, \frac{2}{2}\right)=(-6,1)$

El foco es $\ (−6,7)$ y la distancia entre éste y el centro es de 6 unidades, o $\ c$ . Encuentra $\ b$ .

\ (\\ comenzar {alineado}
36 &=b^ {2} +16\\
20 &=b^ {2}\\
b &=\ sqrt {20} =2\ sqrt {5}
\ end {alineado}\)

La ecuación de la hipérbola es $\ \frac{(y-1)^{2}}{16}-\frac{(x+6)^{2}}{20}=1$ .

Revisar

Encuentra el centro, vértices, focos y asíntotas de cada hipérbola abajo.

$\ \frac{(x+5)^{2}}{25}-\frac{(y+1)^{2}}{36}=1$
$\ (y+2)^{2}-16(x-6)^{2}=16$
$\ \frac{(y-2)^{2}}{9}-\frac{(x-3)^{2}}{49}=1$
$\ 25 x^{2}-64(y-6)^{2}=1600$
$\ (x-8)^{2}-\frac{(y-4)^{2}}{9}=1$
$\ 81(y+4)^{2}-4(x+5)^{2}=324$
Grafica la hipérbola en #1.
Grafica la hipérbola en #2.
Grafica la hipérbola en #5.
Grafica la hipérbola en #6.

Usando la siguiente información, encuentra la ecuación de cada hipérbola.

vértices: $\ (−2,−3)$ y $\ (8,−3)b=7$
vértices: $\ (5,6)$ y $\ (5,−12)$ enfoque: $\ (5,−15)$
asíntota: eje transversal $\ y+3=\frac{4}{9}(x+1)$ horizontal
focos: $\ (−11,−4)$ y $\ (1,−4)$ vértice: $\ (−8,−4)$
Extensión Reescribir la ecuación de la hipérbola,
$\ x^{2}-4 y^{2}+490 x-16 y+1013=0$ en forma normalizada, completando el cuadrado tanto para los términos como para $\ x$ los $\ y$ términos.

Respuestas para problemas de revisión

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.9.

Atribuciones de imagen

[Figura 1]
Crédito: Ben Salter
Fuente: https://www.flickr.com/photos/ben_salter/2348052408

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Hipérbolas Centradas en (h, k)

Hipérbolas Centradas en (h, k)

Ejemplos

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Revisar

Respuestas para problemas de revisión

Atribuciones de imagen

Support Center

How can we help?