Estimación
- Última actualización
- Guardar como PDF
- Page ID
- 151206
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Video
Video: Estimación (11:40)
Introducción
En nuestra Introducción a la Inferencia definimos estimaciones puntuales y estimaciones de intervalos.
- En la estimación puntual, estimamos un parámetro desconocido utilizando un solo número que se calcula a partir de los datos de la muestra.
- En la estimación de intervalos, estimamos un parámetro desconocido usando un intervalo de valores que probablemente contenga el valor verdadero de ese parámetro (y declaramos cuán seguros estamos de que este intervalo efectivamente captura el valor verdadero del parámetro).
En esta sección, introduciremos el concepto de intervalo de confianza y aprenderemos a calcular intervalos de confianza para medias poblacionales y proporciones poblacionales (cuando se cumplan ciertas condiciones).
En la Unidad 4B, veremos que los intervalos de confianza son útiles siempre que se deseen utilizar datos para estimar un parámetro de población desconocido, incluso cuando este parámetro se estime utilizando múltiples variables (como nuestros casos: CC, CQ, QQ).
Por ejemplo, podemos construir intervalos de confianza para la pendiente de una ecuación de regresión o el coeficiente de correlación. Al hacerlo siempre estamos usando nuestros datos para proporcionar una estimación de intervalo para un parámetro de población desconocido (la pendiente VERDADERA, o el coeficiente de correlación VERDADERO).
Estimación de puntos
Objetivos de aprendizaje
LO 4.29: Determinar y utilizar las estimaciones puntuales correctas para parámetros poblacionales especificados.
La estimación puntual es la forma de inferencia estadística en la que, con base en los datos de la muestra, estimamos el parámetro desconocido de interés utilizando un solo valor (de ahí la estimación del punto del nombre). Como ilustran los dos ejemplos siguientes, esta forma de inferencia es bastante intuitiva.
EJEMPLO:
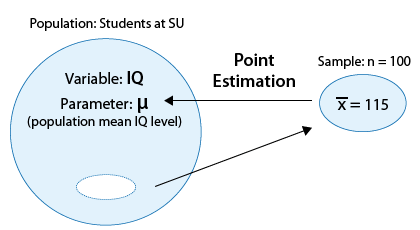
Supongamos que estamos interesados en estudiar los niveles de CI de los estudiantes de Smart University (SU). En particular (ya que el nivel de CI es una variable cuantitativa), nos interesa estimar µ (mu), el nivel medio de CI de todos los estudiantes de la SU.
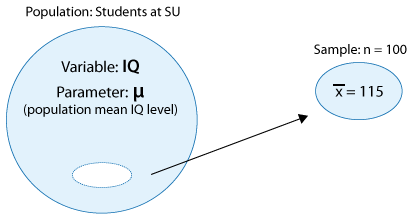
Se eligió una muestra aleatoria de 100 estudiantes de SU, y su nivel medio de CI (muestra) fue de 115 (barra x).
Si quisiéramos estimar µ (mu), el nivel de CI medio poblacional, por un solo número basado en la muestra, tendría sentido intuitivo utilizar la cantidad correspondiente en la muestra, la media de la muestra que es 115. Decimos que 115 es la estimación puntual para µ (mu), y en general, siempre usaremos la media muestral (barra x) como estimador de puntos para µ (mu). (Tenga en cuenta que cuando hablamos del valor específico (115), usamos el término estimación, y cuando hablamos en general sobre la estadística x-bar, usamos el término estimador. La siguiente figura resume este ejemplo:
Aquí hay otro ejemplo.
EJEMPLO:
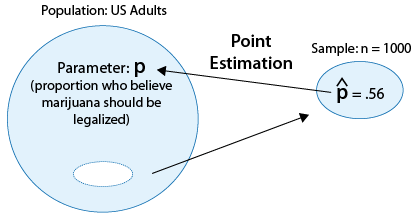
Supongamos que nos interesan las opiniones de los adultos estadunidenses respecto a la legalización del uso de la mariguana. En particular, nos interesa el parámetro p, la proporción de adultos estadounidenses que creen que se debe legalizar la marihuana.
Supongamos que una encuesta de 1,000 adultos estadounidenses encuentra que 560 de ellos creen que la marihuana debería ser legalizada. Si quisiéramos estimar p, la proporción poblacional, utilizando un solo número basado en la muestra, tendría sentido intuitivo usar la cantidad correspondiente en la muestra, la proporción muestral p-hat = 560/1000 = 0.56. Decimos en este caso que 0.56 es la estimación puntual para p, y en general, siempre usaremos p-hat como estimador de puntos para p. (Tenga en cuenta, nuevamente, que cuando hablamos del valor específico (0.56), usamos el término estimación, y cuando hablamos en general sobre la estadística p-hat, utilizamos el término estimador. Aquí hay un resumen visual de este ejemplo:
¿Recibí esto? : Estimación de puntos
Propiedades Deseadas de Estimadores de Puntos
Es posible que sientas que al ser tan intuitivo, podrías haber averiguado la estimación de puntos por tu cuenta, incluso sin el beneficio de todo un curso de estadística. Ciertamente, nuestra intuición nos dice que el mejor estimador para la media poblacional (mu, µ) debe ser x-bar, y el mejor estimador para la proporción poblacional p debe ser p-hat.
La teoría de probabilidad hace más que esto; en realidad da una explicación (más allá de la intuición) por qué x-bar y p-hat son las buenas opciones como estimadores de puntos para µ (mu) y p, respectivamente. En la sección Distribuciones de Muestreo de la unidad Probabilidad, aprendimos sobre la distribución muestral de la barra x y encontramos que mientras se tome una muestra al azar, la distribución de medias muestrales se centra exactamente en el valor de la media poblacional.
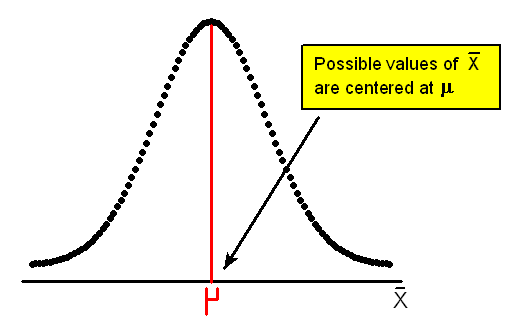
Por lo tanto, se dice que nuestra estadística, x-bar, es un estimador imparcial para µ (mu). Cualquier media de la muestra en particular podría llegar a ser menor que la media de la población real, o podría resultar ser más. Pero a la larga, tales medios de muestra están “en el blanco” en el sentido de que no subestimarán con más o menos frecuencia de lo que sobreestiman.
Asimismo, aprendimos que la distribución muestral de la proporción muestral, p-hat, se centra en la proporción poblacional p (siempre y cuando la muestra se tome al azar), haciendo de p-hat un estimador imparcial para p.
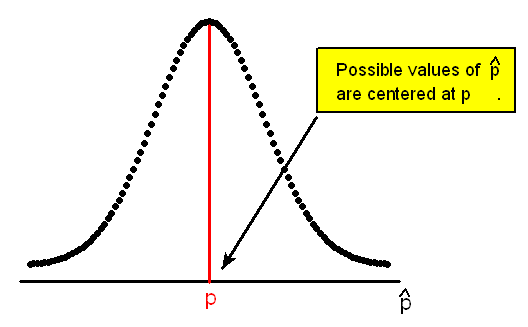
Como se afirma en la introducción, la teoría de la probabilidad juega un papel esencial a medida que establecemos resultados para la inferencia estadística. Nuestra afirmación anterior de que la media muestral y la proporción muestral son estimadores imparciales es la primera instancia de este tipo.
Importancia de Muestreo y Diseño
Observe cuán importantes son los principios de muestreo y diseño para nuestros resultados anteriores: si la muestra de adultos estadounidenses en (ejemplo 2 en la página anterior) no fue aleatoria, sino que incluyó predominantemente estudiantes universitarios, entonces 0.56 sería una estimación sesgada para p, la proporción de todos los adultos estadounidenses que creen se debe legalizar la mariguana.
Si el diseño de la encuesta fuera defectuoso, como cargar la pregunta con un recordatorio sobre los peligros de la marihuana que conducen a drogas duras, o un recordatorio sobre los beneficios de la marihuana para los pacientes con cáncer, entonces 0.56 estaría sesgado en el lado bajo o alto, respectivamente.
Precaución
Nuestras estimaciones puntuales son estimaciones verdaderamente imparciales para el parámetro poblacional solo si la muestra es aleatoria y el diseño del estudio no es defectuoso.
Error estándar y tamaño de la muestra
No solo la media de la muestra y la proporción de la muestra en el objetivo siempre que las muestras sean aleatorias, sino que su precisión mejora a medida que aumenta el tamaño de la muestra.
Nuevamente, aquí hay dos “capas” para explicar esto.
Intuitivamente, los tamaños de muestra más grandes nos dan más información con la que precisar la verdadera naturaleza de la población. Por lo tanto, podemos esperar que la media muestral y la proporción muestral obtenida de una muestra más grande estén más cerca de la media y proporción de la población, respectivamente. En extremo, cuando se muestrea toda la población (que se llama censo), la media muestral y la proporción muestral coincidirán exactamente con la media poblacional y la proporción población.Aquí hay otra capa que, nuevamente, proviene de lo que aprendimos sobre las distribuciones muestrales de la media muestral y la proporción muestral. Usemos la media de la muestra para la explicación.
Recordemos que la distribución muestral de la media muestral x-bar está, como mencionamos anteriormente, centrada en la media poblacional µ (mu) y tiene un error estándar (desviación estándar del estadístico, x-bar) de
desviación estándar de\(\dfrac{\sigma}{\sqrt{n}}\)
Como resultado, a medida que aumenta el tamaño de la muestra n, la distribución muestral de la barra x se extiende menos. Esto significa que los valores de la barra x que se basan en una muestra más grande tienen más probabilidades de estar más cerca de µ (mu) (como ilustra la siguiente figura):
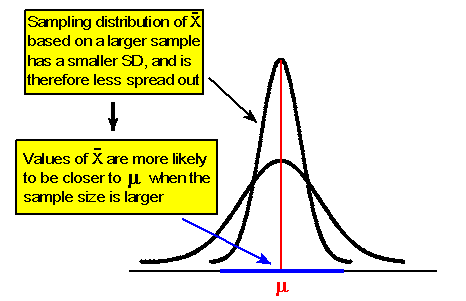
Del mismo modo, dado que la distribución de muestreo de p-hat se centra en p y tiene un
desviación estándar de\(\sqrt{\dfrac{p(1-p)}{n}}\)
que disminuye a medida que aumenta el tamaño de la muestra, es más probable que los valores de p-hat estén más cerca de p cuando el tamaño de la muestra es mayor.
Otro Estimador de Puntos
Otro ejemplo de estimador puntual es el uso de la desviación estándar de la muestra,
\(s=\sqrt{\dfrac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}{n-1}}\)
para estimar la desviación estándar poblacional, σ (sigma).
En este curso, no nos preocuparemos por estimar la desviación estándar de la población por su propio bien, pero dado que a menudo sustituiremos las desviaciones estándar de la muestra por σ (sigma) al estandarizar la media de la muestra, vale la pena señalar que s es un estimador imparcial para σ (sigma).
Si hubiéramos dividido por n en lugar de n — 1 en nuestro estimador para la desviación estándar poblacional, entonces a la larga nuestra varianza muestral sería culpable de una ligera subestimación. División por n — 1 logra el objetivo de hacer que este estimador de puntos sea imparcial.
La razón por la que nuestra fórmula para s, introducida en la unidad de Análisis Exploratorio de Datos, implica la división por n — 1 en lugar de por n es el hecho de que deseamos utilizar estimadores imparciales en la práctica.
Resumimos
- Utilizamos p-hat (proporción muestral) como estimador puntual para p (proporción poblacional). Es un estimador imparcial: su distribución a largo plazo se centra en p siempre que la muestra sea aleatoria.
- Utilizamos la barra x (media muestral) como estimador puntual para µ (mu, media poblacional). Es un estimador imparcial: su distribución a largo plazo se centra en µ (mu) siempre y cuando la muestra sea aleatoria.
- En ambos casos, cuanto mayor sea el tamaño de la muestra, más preciso es el estimador de puntos. En otras palabras, cuanto mayor sea el tamaño de la muestra, más probable es que la media muestral (proporción) esté cerca de la media de la población desconocida (proporción).
¿Recibí esto? : Propiedades de Estimadores de Puntos
Estimación de Intervalo
La estimación de puntos es simple e intuitiva, pero también un poco problemática. He aquí por qué:
Cuando estimamos μ (mu) por la barra x media de la muestra, casi se garantiza que cometemos algún tipo de error. Aunque sabemos que los valores de x-bar caen alrededor de μ (mu), es muy poco probable que el valor de x-bar caiga exactamente en μ (mu).
Dado que tales errores son un hecho de la vida para las estimaciones puntuales (por el mero hecho de que estamos basando nuestra estimación en una muestra que es una pequeña fracción de la población), estas estimaciones son en sí mismas de utilidad limitada, a menos que seamos capaces de cuantificar el alcance del error de estimación. La estimación de intervalos aborda este problema. La idea detrás de la estimación del intervalo es, por lo tanto, mejorar las estimaciones puntuales simples proporcionando información sobre el tamaño del error adjunto.
En esta introducción, proporcionaremos ejemplos que le darán una sólida intuición sobre la idea básica detrás de la estimación de intervalos.
EJEMPLO:
Consideremos el ejemplo que discutimos en la sección de estimación de puntos:
Supongamos que estamos interesados en estudiar los niveles de CI de los estudiantes que asisten a Smart University (SU). En particular (ya que el nivel de CI es una variable cuantitativa), nos interesa estimar μ (mu), el nivel medio de CI de todos los estudiantes en SU. Se eligió una muestra aleatoria de 100 estudiantes de SU, y su nivel medio de CI (muestra) fue de 115 (barra x).
En la estimación puntual se utilizó x-bar = 115 como estimación puntual para μ (mu). Sin embargo, no teníamos idea de cuál podría ser el error de estimación involucrado en dicha estimación. La estimación de intervalos lleva la estimación de puntos un paso más allá y dice algo así como:
“Estoy 95% seguro de que al usar la estimación puntual x-bar = 115 para estimar μ (mu), estoy fuera por no más de 3 puntos IQ. En otras palabras, estoy 95% seguro de que μ (mu) está dentro de 3 de 115, o entre 112 (115 — 3) y 118 (115 + 3)”.
Otra forma más de decir lo mismo es: Estoy 95% seguro de que μ (mu) está en algún lugar (o cubierto por) el intervalo (112,118). (Comentario: En este punto no debes preocuparte, ni tratar de averiguar, cómo conseguimos estos números. Eso lo haremos más tarde. Todo lo que queremos hacer aquí es asegurarnos de que entiendas la idea).
Obsérvese que si bien la estimación puntual proporcionó solo un número como estimación para μ (mu) de 115, la estimación de intervalo proporciona un intervalo completo de “valores plausibles” para μ (mu) (entre 112 y 118), y también agrega el nivel de nuestra confianza de que este intervalo efectivamente incluye el valor de μ (mu) a nuestra estimación ( en nuestro ejemplo, 95% de confianza). Por lo tanto, el intervalo (112,118) se denomina “un intervalo de confianza del 95% para μ (mu)”.
Veamos otro ejemplo:
EJEMPLO:
Consideremos el segundo ejemplo de la sección de estimación de puntos.
Supongamos que nos interesan las opiniones de los adultos estadunidenses respecto a la legalización del uso de la mariguana. En particular, nos interesa el parámetro p, la proporción de adultos estadounidenses que creen que se debe legalizar la marihuana.
Supongamos que una encuesta de 1,000 adultos estadounidenses encuentra que 560 de ellos creen que la marihuana debería ser legalizada.
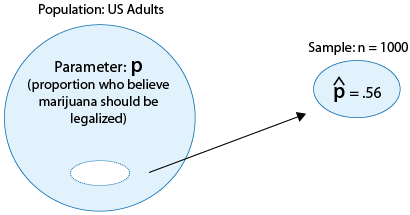
Si quisiéramos estimar p, la proporción poblacional, por un solo número basado en la muestra, tendría sentido intuitivo utilizar la cantidad correspondiente en la muestra, la proporción muestral p-hat = 560/1000=0.56.
La estimación de intervalos llevaría esto un paso más allá y diría algo como:
“Estoy 90% seguro de que al usar 0.56 para estimar la verdadera proporción poblacional, p, estoy fuera por (o, tengo un error de) no más de 0.03 (o 3 puntos porcentuales). En otras palabras, estoy 90% seguro de que el valor real de p está en algún lugar entre 0.53 (0.56 — 0.03) y 0.59 (0.56 + 0.03).”
Otra forma más de decir esto es: “Estoy 90% seguro de que p está cubierto por el intervalo (0.53, 0.59)”.
En este ejemplo, (0.53, 0.59) es un intervalo de confianza del 90% para p.
Vamos a resumir
Los dos ejemplos nos mostraron que la idea detrás de la estimación del intervalo es, en lugar de proporcionar solo un número para estimar un parámetro de interés desconocido, proporcionar un intervalo de valores plausibles del parámetro más un nivel de confianza de que el valor del parámetro está cubierto por este intervalo.
Ahora vamos a entrar en más detalles y aprender cómo se crean e interpretan estos intervalos de confianza en contexto. Como verás, las ideas que se desarrollaron en la sección “Distribuciones de Muestreo” de la unidad Probabilidad volverán a ser muy importantes. Recordemos que para la estimación de puntos, nuestra comprensión de las distribuciones de muestreo conduce a la verificación de que nuestras estadísticas son imparciales y nos da fórmulas precisas para el error estándar de nuestras estadísticas.
Comenzaremos discutiendo los intervalos de confianza para la media poblacional μ (mu), y luego discutiremos los intervalos de confianza para la proporción poblacional p.
Medios de Población (Parte 1)
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.30: Interpretar intervalos de confianza para parámetros poblacionales en contexto.
Objetivos de aprendizaje
LO 4.31: Encuentre intervalos de confianza para la media poblacional usando la fórmula de intervalo de confianza basada en la distribución normal (Z) (cuando se cumplan las condiciones requeridas) y realice cálculos de tamaño de muestra.
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Objetivos de aprendizaje
LO 6.24: Explicar la conexión entre la distribución muestral de un estadístico, y sus propiedades como estimador puntual.
Objetivos de aprendizaje
LO 6.25: Explicar lo que representa un intervalo de confianza y determinar cómo los cambios en el tamaño de la muestra y el nivel de confianza afectan la precisión del intervalo de confianza.
Video
Video: Medios poblacionales — Parte 1 (11:14)
Como se mencionó en la introducción, iniciaremos nuestra discusión sobre la estimación de intervalos con estimación de intervalos para la media poblacional μ (mu). Comenzaremos mostrando cómo se construye un intervalo de confianza del 95%, y luego generalizaremos a otros niveles de confianza. También discutiremos cuestiones prácticas relacionadas con la estimación de intervalos.
Recordemos el ejemplo de IQ:
EJEMPLO:
Supongamos que estamos interesados en estudiar los niveles de CI de los estudiantes de Smart University (SU). En particular (ya que el nivel de CI es una variable cuantitativa), nos interesa estimar μ (mu), el nivel medio de CI de todos los estudiantes de la SU.
Supondremos que a partir de investigaciones pasadas sobre puntajes de CI en diferentes universidades, se sabe que la desviación estándar del coeficiente intelectual en tales poblaciones es σ (sigma) = 15. Para estimar μ (mu), se eligió una muestra aleatoria de 100 estudiantes de SU, y se calcula su nivel medio de CI (muestra) (supongamos, por ahora, que aún no hemos encontrado la media muestral).
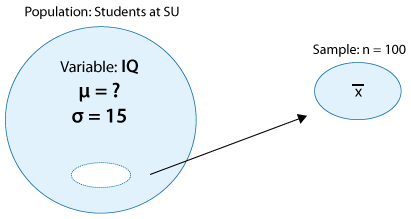
Ahora mostraremos la razón de construir un intervalo de confianza del 95% para la media poblacional μ (mu).
- Aprendimos en la sección de probabilidad “Distribuciones de muestreo” que según el teorema del límite central, la distribución muestral de la media muestral x-bar es aproximadamente normal con una media de μ (mu) y desviación estándar de σ/sqrt (n) = sigma/sqrt (n). En nuestro ejemplo, entonces, (donde σ (sigma) = 15 y n = 100), los posibles valores de x-bar, el nivel de CI medio muestral de 100 estudiantes elegidos al azar, es aproximadamente normal, con media μ (mu) y desviación estándar 15/sqrt (100) = 1.5.
- A continuación, recordamos y aplicamos la Regla de Desviación Estándar para la distribución normal, y en particular su segunda parte: Existe un 95% de probabilidad de que la media muestral que encontraremos en nuestra muestra se encuentre dentro de 2 * 1.5 = 3 de μ (mu).
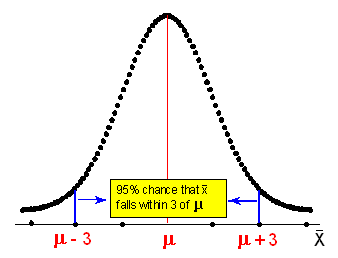
Obviamente, si existe cierta distancia entre la media muestral y la media poblacional, podemos describir esa distancia comenzando en cualquiera de los dos valores. Entonces, si la media muestral (x-bar) cae dentro de una cierta distancia de la media poblacional μ (mu), entonces la media poblacional μ (mu) cae dentro de la misma distancia de la media muestral.
Por lo tanto, la afirmación, “Existe un 95% de probabilidad de que la media de la muestra x-bar caiga dentro de las 3 unidades de μ (mu)” puede reformularse como: “Estamos 95% seguros de que la media poblacional μ (mu) se encuentra dentro de las 3 unidades de la barra x que encontramos en nuestra muestra”.
Entonces, si por casualidad obtenemos una media muestral de x-bar = 115, entonces estamos 95% seguros de que μ (mu) cae dentro de 3 unidades de 115, o en otras palabras que μ (mu) está cubierto por el intervalo (115 — 3, 115 + 3) = (112,118).
(En páginas posteriores, utilizaremos razonamientos similares para desarrollar una fórmula general para un intervalo de confianza).
Comentario:
- Tenga en cuenta que el primer fraseo es sobre x-bar, que es una variable aleatoria; por eso tiene sentido usar lenguaje de probabilidad. Pero el segundo fraseo es sobre μ (mu), que es un parámetro, y así es un valor “fijo” que no cambia, y por eso no debemos usar lenguaje de probabilidad para discutirlo. En estos problemas, es nuestra barra x la que cambiará cuando repitamos el proceso, no μ (mu). Este punto se aclarará después de realizar las actividades que siguen.
El Caso General
Generalicemos el ejemplo de CI. Supongamos que estamos interesados en estimar la media poblacional desconocida (μ, mu) a partir de una muestra aleatoria de tamaño n Además, asumimos que se conoce la desviación estándar poblacional (σ, sigma).
Precaución
Nota: El supuesto de que se conoce la desviación estándar poblacional no suele ser realista, sin embargo, lo hacemos aquí para poder introducir los conceptos en el caso más simple. Posteriormente, discutiremos los cambios que hay que hacer cuando no conocemos la desviación estándar poblacional.
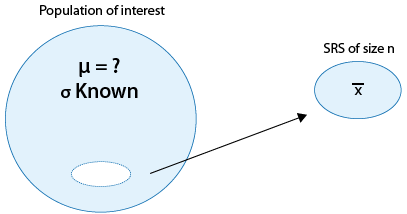
Los valores de x-bar siguen una distribución normal con (desconocida) media μ (mu) y desviación estándar σ/sqrt (n) =sigma/sqrt (n) (conocida, ya que se conocen tanto σ, sigma y n). En la regla de desviación estándar, afirmamos que aproximadamente el 95% de los valores se encuentran dentro de 2 desviaciones estándar de μ (mu). A partir de ahora, seremos un poco más precisos y usaremos la tabla normal estándar para encontrar el valor exacto para 95%.
Nuestra imagen es la siguiente:
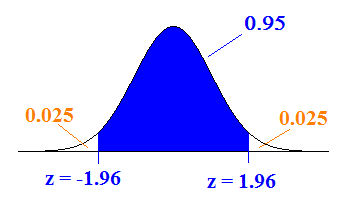
Intente usar el applet en el post para Aprender haciendo — Variables aleatorias normales para encontrar el corte ilustrado anteriormente.
También podemos verificar el puntaje z usando una calculadora o tabla encontrando el puntaje z con el área de 0.025 a la izquierda (lo que nos daría -1.96) o con el área a la izquierda de 0.975 = 0.95 + 0.025 (lo que nos daría +1.96).
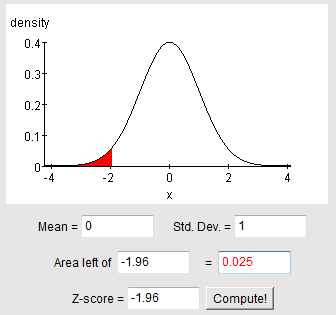
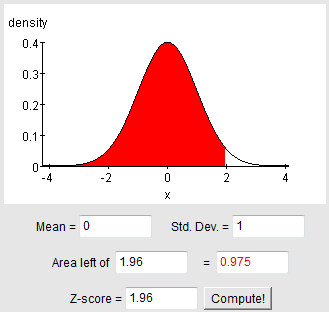
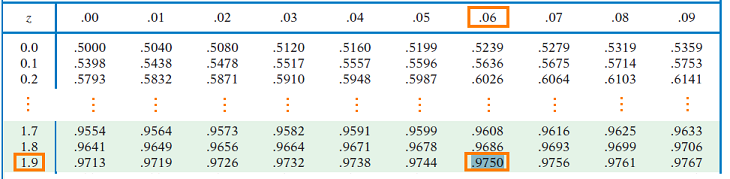
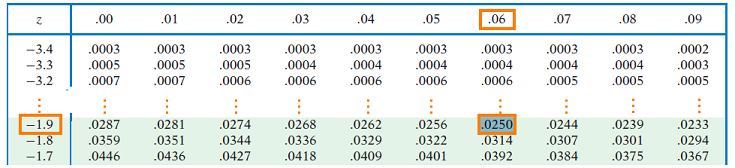
Así, existe un 95% de probabilidad de que nuestra muestra media de barra x caiga dentro de 1.96*σ/sqrt (n) = 1.96*sigma/sqrt (n) de μ (mu).
Lo que significa que estamos 95% seguros de que μ (mu) cae dentro de 1.96*σ/sqrt (n) = 1.96*sigma/sqrt (n) de nuestra muestra media de barra x.
Aquí, entonces, está el resultado general:
Supongamos que se toma una muestra aleatoria de tamaño n de una población normal de valores para una variable cuantitativa cuya media (μ, mu) es desconocida, cuando se da la desviación estándar (σ, sigma).
Un intervalo de confianza (IC) del 95% para μ (mu) es:
\(\bar{x} \pm 1.96 * \dfrac{\sigma}{\sqrt{n}}\)
Comentario:
- Tenga en cuenta que por ahora requerimos que se conozca la desviación estándar poblacional (σ, sigma). Prácticamente, σ (sigma) rara vez se conoce, pero para algunos casos, especialmente cuando se ha realizado mucha investigación sobre la variable cuantitativa cuya media estamos estimando (como IQ, estatura, peso, puntuaciones en pruebas estandarizadas), es razonable suponer que σ (sigma) es conocido. Eventualmente, veremos cómo proceder cuando σ (sigma) es desconocida, y se debe estimar con la desviación estándar de la muestra.
Veamos otro ejemplo.
EJEMPLO:
Un investigador educativo estuvo interesado en estimar μ (mu), la puntuación media en la parte de matemáticas del SAT (SAT-M) de todos los estudiantes de colegios comunitarios en su estado. Para ello, el investigador ha elegido una muestra aleatoria de 650 estudiantes de colegios comunitarios de su estado, y encontró que su puntaje promedio SAT-M es de 475. Con base en un gran cuerpo de investigación que se realizó en el SAT, se sabe que las puntuaciones siguen aproximadamente una distribución normal con la desviación estándar σ (sigma) =100.
Aquí hay una representación visual de esta historia, que resume la información proporcionada:
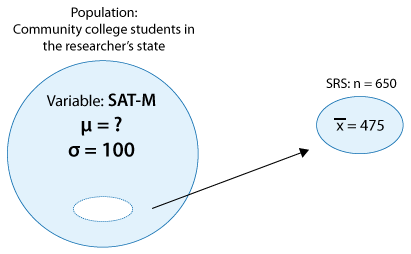
Con base en esta información, calculemos μ (mu) con un intervalo de confianza del 95%.
Usando la fórmula que desarrollamos anteriormente
\(\bar{x} \pm 1.96 * \dfrac{\simga}{\sqrt{n}}\)
el intervalo de confianza del 95% para μ (mu) es:
\ begin {aligned}
475\ pm 1.96 *\ frac {100} {\ sqrt {650}} &=\ left (475-1.96 *\ frac {100} {\ sqrt {650}}, 475+1.96 *\ frac {100} {\ sqrt {650}}\ derecha)\\ & =( 475-7.7.475+7.7)\\ & =( 467.7.475+7.7)\
& =( 467.7.475+7.7)\
& =( 467.7.475+7.7)\ 3,482.7)
\ final {alineado}
Por lo general, proporcionaremos información sobre cómo redondear su respuesta final. En este caso, un decimal es suficiente precisión para este escenario. También podrías redondear al número entero más cercano sin mucha pérdida de información aquí.
Aún no hemos terminado. Una parte igualmente importante es interpretar lo que esto significa en el contexto del problema.
Estamos 95% seguros de que la puntuación media SAT-M de todos los estudiantes de colegios comunitarios en el estado investigador está cubierta por el intervalo (467.3, 482.7). Obsérvese que el intervalo de confianza se obtuvo tomando 475 ± 7.7. Esto significa que estamos 95% seguros de que al usar la media muestral (x-bar = 475) para estimar μ (mu), nuestro error no supera los 7.7 puntos.
Aprender haciendo: Intervalos de confianza: Medios #1
Acabas de ganar práctica informática e interpretar un intervalo de confianza para una media poblacional. Tenga en cuenta que la forma en que se usa un intervalo de confianza es que esperamos que el intervalo contenga la media poblacional μ (mu). Es por ello que lo llamamos un “intervalo para la media poblacional”.
La siguiente actividad está diseñada para ayudarle a comprender mejor el razonamiento subyacente detrás de la interpretación de los intervalos de confianza. En particular, obtendrá una comprensión más profunda de por qué decimos que estamos “95% seguros de que la media poblacional está cubierta por el intervalo”.
Aprende haciendo: Conexión entre intervalos de confianza y distribuciones de muestreo con video (1:18)
Acabamos de ver que una interpretación de un intervalo de confianza del 95% es que estamos 95% seguros de que la media poblacional (μ, mu) está contenida en el intervalo. Otra interpretación útil en la práctica es que, dados los datos, el intervalo de confianza representa el conjunto de valores plausibles para la media poblacional μ (mu).
EJEMPLO:
Como ilustración, volvamos al ejemplo del puntaje promedio de SAT-Math de los estudiantes de la universidad comunitaria. Recordemos que habíamos construido el intervalo de confianza (467.3, 482.7) para el puntaje SAT-M promedio desconocido para todos los estudiantes de colegios comunitarios.
Aquí hay una manera en que podemos usar el intervalo de confianza:
¿Los resultados de este estudio proporcionan evidencia de que μ (mu), la puntuación media SAT-M de los estudiantes de colegios comunitarios, es menor que la puntuación media SAT-M en la población general de estudiantes universitarios de ese estado (que es 480)?
Se encontró que el intervalo de confianza del 95% para μ (mu) fue (467.3, 482.7). Obsérvese que 480, la puntuación media SAT-M en la población general de estudiantes universitarios en ese estado, cae dentro del intervalo, lo que significa que es uno de los valores plausibles para μ (mu).
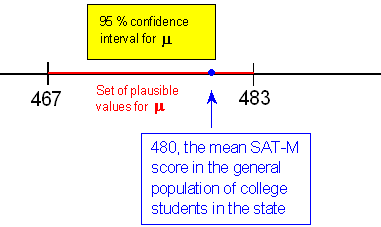
Esto significa que μ (mu) podría ser 480 (o incluso superior, hasta 483), y por lo tanto no podemos concluir que la puntuación media SAT-M entre los estudiantes de colegios comunitarios en el estado sea menor que la media en la población general de estudiantes universitarios de ese estado. (Obsérvese que el hecho de que la mayoría de los valores plausibles para μ (mu) caigan por debajo de 480 no es una consideración aquí.)
\(\bar{x} \pm 1.96 * \dfrac{\sigma}{\sqrt{n}}\)
el intervalo de confianza del 95% para μ (mu) es:
\ begin {aligned}
475\ pm 1.96 *\ frac {100} {\ sqrt {650}} &=\ left (475-1.96 *\ frac {100} {\ sqrt {650}}, 475+1.96 *\ frac {100} {\ sqrt {650}}\ derecha)\\ & =( 475-7.7.475+7.7)\\ & =( 467.7.475+7.7)\
& =( 467.7.475+7.7)\
& =( 467.7.475+7.7)\ 3,482.7)
\ final {alineado}
Por lo general, proporcionaremos información sobre cómo redondear su respuesta final. En este caso, un decimal es suficiente precisión para este escenario. También podrías redondear al número entero más cercano sin mucha pérdida de información aquí.
Aún no hemos terminado. Una parte igualmente importante es interpretar lo que esto significa en el contexto del problema.
Estamos 95% seguros de que la puntuación media SAT-M de todos los estudiantes de colegios comunitarios en el estado investigador está cubierta por el intervalo (467.3, 482.7). Obsérvese que el intervalo de confianza se obtuvo tomando 475 ± 7.7. Esto significa que estamos 95% seguros de que al usar la media muestral (x-bar = 475) para estimar μ (mu), nuestro error no supera los 7.7 puntos.
Medios de Población (Parte 2)
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.30: Interpretar intervalos de confianza para parámetros poblacionales en contexto.
Objetivos de aprendizaje
LO 4.31: Encuentre intervalos de confianza para la media poblacional usando la fórmula de intervalo de confianza basada en la distribución normal (Z) (cuando se cumplan las condiciones requeridas) y realice cálculos de tamaño de muestra.
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Objetivos de aprendizaje
LO 6.24: Explicar la conexión entre la distribución muestral de un estadístico, y sus propiedades como estimador puntual.
Objetivos de aprendizaje
LO 6.25: Explicar lo que representa un intervalo de confianza y determinar cómo los cambios en el tamaño de la muestra y el nivel de confianza afectan la precisión del intervalo de confianza.
Video
Video: Medios poblacionales — Parte 2 (4:04)
Otros Niveles de Confianza
El 95% es el nivel de confianza más utilizado. Sin embargo, es posible que deseemos aumentar nuestro nivel de confianza y producir un intervalo que es casi seguro que contenga μ (mu). Específicamente, es posible que queramos reportar un intervalo para el cual estamos 99% seguros de que contiene la media de población desconocida, en lugar de solo 95%.
Usando el mismo razonamiento que en el último comentario, con el fin de crear un intervalo de confianza del 99% para μ (mu), deberíamos preguntar: ¿Existe una probabilidad de 0.99 de que cualquier variable aleatoria normal tome valores dentro de cuántas desviaciones estándar de su media? La respuesta precisa es 2.576, y por lo tanto, un intervalo de confianza del 99% para μ (mu) es:
\(\bar{x} \pm 2.576 * \dfrac{\sigma}{\sqrt{n}}\)
Otro nivel de confianza comúnmente utilizado es un nivel de confianza del 90%. Dado que existe una probabilidad de 0.90 de que cualquier variable aleatoria normal tome valores dentro de 1.645 desviaciones estándar de su media, el intervalo de confianza del 90% para μ (mu) es:
\(\bar{x} \pm 1.645 * \dfrac{\sigma}{\sqrt{n}}\)
EJEMPLO:
Volvamos a nuestro primer ejemplo, el ejemplo de IQ:
El nivel de CI de los estudiantes de una universidad en particular tiene una media desconocida (μ, mu) y una desviación estándar conocida σ (sigma) =15. Se encontró que una muestra aleatoria simple de 100 estudiantes tiene un coeficiente intelectual medio muestral de 115 (barra x). Estimar μ (mu) con un intervalo de confianza de 90%, 95% y 99%.
Un intervalo de confianza del 90% para μ (mu) es:
\(\bar{x} \pm 1.645 \dfrac{\sigma}{\sqrt{n}} = 115 \pm 1.645(\dfrac{15}{\sqrt{100}}) = 115 \pm 2.5 = (112.5, 117.5)\).
Un intervalo de confianza del 95% para μ (mu) es:
\(\bar{x} \pm 1.96 \dfrac{\sigma}{\sqrt{n}} = 115 \pm 1.96 (\dfrac{15}{\sqrt{100}}) = 115 \pm 2.9 = (112.1, 117.9)\).
Un intervalo de confianza del 99% para μ (mu) es:
\(\bar{x} \pm 2.576 \dfrac{\sigma}{\sqrt{n}} = 115 \pm 2.576 (\dfrac{15}{\sqrt{100}} = 115 \pm 4.0 = (111,119)\).
El propósito de esta siguiente actividad es darte una práctica guiada en el cálculo e interpretación de intervalos de confianza, y sacar conclusiones a partir de ellos.
¿Recibí esto? : Intervalos de confianza: Media #1
Nota del ejemplo anterior y del anterior “¿Conseguí esto?” actividad, que cuanto más confianza requiero, mayor será el intervalo de confianza para μ (mu). El intervalo de confianza del 99% es más amplio que el intervalo de confianza del 95%, que es más ancho que el intervalo de confianza del 90%.

Esto no es muy sorprendente, dado que en el intervalo del 99% multiplicamos la desviación estándar del estadístico por 2.576, en el 95% por 2, y en el 90% solo por 1.645. Más allá de esta explicación numérica, hay una explicación intuitiva muy clara y una implicación importante de este resultado.
Empecemos con la explicación intuitiva. Cuanto más seguro quiero estar de que el intervalo contenga el valor de μ (mu), más valores plausibles debe incluir el intervalo para dar cuenta de esa certeza extra. Estoy 95% seguro de que el valor de μ (mu) es uno de los valores en el intervalo (112.1, 117.9). Para estar 99% seguro de que uno de los valores en el intervalo es el valor de μ (mu), necesito incluir más valores, y así proporcionar un intervalo de confianza más amplio.
Aprende haciendo: Visualizando la Relación entre Confianza y Ancho
En nuestro ejemplo, el intervalo de confianza del 99% más amplio (111, 119) nos da una estimación menos precisa sobre el valor de μ (mu) que el intervalo de confianza del 90% más estrecho (112.5, 117.5), porque el intervalo más pequeño se estrecha en los valores plausibles de μ (mu).
La implicación práctica importante aquí es que los investigadores deben decidir si prefieren exponer sus resultados con un mayor nivel de confianza o producir un intervalo más preciso. En otras palabras,
Precaución
Existe una compensación entre el nivel de confianza y la precisión con la que se estima el parámetro.
El precio que tenemos que pagar por un mayor nivel de confianza es que la media poblacional desconocida se estimará con menor precisión (es decir, con un intervalo de confianza más amplio). Si quisiéramos estimar μ (mu) con más precisión (es decir, un intervalo de confianza más estrecho), necesitaremos sacrificar y reportar un intervalo con un nivel de confianza más bajo.
¿Recibí esto? : Intervalos de confianza: Media #2
Hasta ahora hemos desarrollado el intervalo de confianza para la media poblacional “desde cero” basado en los resultados de la probabilidad, y discutimos el equilibrio entre el nivel de confianza y la precisión del intervalo. El precio que pagas por un mayor nivel de confianza es un menor nivel de precisión del intervalo (es decir, un intervalo más amplio).
¿Hay alguna manera de eludir esta compensación? En otras palabras, ¿hay alguna manera de aumentar la precisión del intervalo (es decir, hacerlo más estrecho) sin comprometer el nivel de confianza? Responderemos a esta pregunta en breve, pero primero necesitaremos comprender más a fondo los diferentes componentes del intervalo de confianza y su estructura.
Comprensión de la estructura general de los intervalos de confianza
Se exploró el intervalo de confianza para μ (mu) para diferentes niveles de confianza, y se encontró que en general, tiene la siguiente forma:
\(\bar{x} \pm z* \dot \dfrac{\sigma}{\sqrt{n}}\)
donde z* es una notación general para el multiplicador que depende del nivel de confianza. Como ya comentamos anteriormente:
- Para un nivel de confianza del 90%, z* = 1.645
- Para un nivel de confianza del 95%, z* = 1.96
- Para un nivel de confianza del 99%, z* = 2.576
Para iniciar nuestra discusión sobre la estructura del intervalo de confianza, denotemos
\(m = z* \dot \dfrac{\sigma}{\sqrt{n}}\)
El intervalo de confianza, entonces, tiene la forma:
\(\bar{x} \pm m\)
Para resumir, tenemos
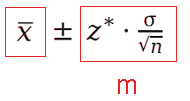
X-bar es la media muestral, el estimador puntual para la media poblacional desconocida (μ, mu).
m se denomina margen de error, ya que representa el error máximo de estimación para un determinado nivel de confianza.
Por ejemplo, para un intervalo de confianza del 95%, estamos 95% seguros de que nuestra estimación no se apartará de la media poblacional verdadera en más de m, el margen de error y m se compone además del producto de dos componentes:
Aquí hay un resumen de los diferentes componentes del intervalo de confianza y su estructura:
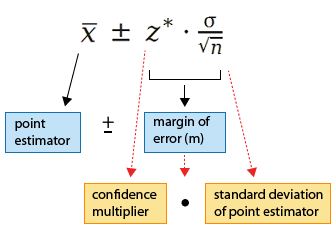
Esta estructura: estimar ± margen de error, donde el margen de error se compone además del producto de un multiplicador de confianza y la desviación estándar de la estadística (o, como veremos, el error estándar) es la estructura general de todos los intervalos de confianza que encontraremos en este curso.
Obviamente, aunque cada intervalo de confianza tenga los mismos componentes, la fórmula para estos componentes es diferente de intervalo de confianza a intervalo de confianza, dependiendo de qué parámetro desconocido pretende estimar el intervalo de confianza.
Dado que la estructura del intervalo de confianza es tal que tiene un margen de error a cada lado de la estimación, se centra en la estimación (en nuestro caso actual, barra x), y su ancho (o largo) es exactamente el doble del margen de error:
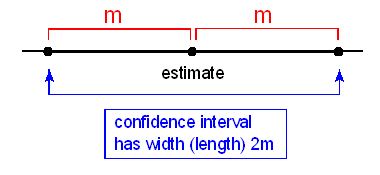
El margen de error, m, es por lo tanto “a cargo” del ancho (o precisión) del intervalo de confianza, y la estimación está a cargo de su ubicación (y no tiene efecto sobre el ancho).
¿Recibí esto? : Margen de Error
Volvamos ahora al intervalo de confianza para la media, y más específicamente, a la pregunta que planteamos al inicio de la página anterior:
¿Hay alguna manera de aumentar la precisión del intervalo de confianza (es decir, hacerlo más estrecho) sin comprometer el nivel de confianza?
Dado que el ancho del intervalo de confianza es una función de su margen de error, veamos de cerca el margen de error del intervalo de confianza para la media y veamos cómo se puede reducir:
\(m = z* \dot \dfrac{\sigma}{\sqrt{n}}\)
Dado que z* controla el nivel de confianza, podemos reformular nuestra pregunta anterior de la siguiente manera:
¿Hay alguna manera de reducir este margen de error que no sea reduciendo z*?
Si miras de cerca el margen de error, verás que la respuesta es sí. Podemos hacerlo aumentando el tamaño de la muestra n (ya que aparece en el denominador).
Muchos estudiantes se preguntan: Intervalos de confianza (media poblacional)
Pregunta : ¿No es cierto que otra forma de reducir el margen de error (para una z* fija) es reducir σ (sigma)?
Respuesta: Si bien es cierto que estrictamente matemáticamente hablando cuanto menor sea el valor de σ (sigma), cuanto menor sea el margen de error, prácticamente hablando no tenemos absolutamente ningún control sobre el valor de σ (sigma) (es decir, no podemos hacerlo más grande o menor). σ (sigma) es el desviación estándar poblacional; es un valor fijo (que aquí asumimos es conocido) que tiene un efecto sobre el ancho del intervalo de confianza (ya que aparece en el margen de error), pero definitivamente no es un valor que podamos cambiar.
Veamos primero un ejemplo y luego expliquemos por qué aumentar el tamaño de la muestra es una forma de aumentar la precisión del intervalo de confianza sin comprometer el nivel de confianza.
EJEMPLO:
Recordemos el ejemplo de IQ:
El nivel de CI de los estudiantes de una universidad en particular tiene una media desconocida (μ, mu) y una desviación estándar conocida de σ (sigma) =15. Se encontró que una muestra aleatoria simple de 100 estudiantes tiene el coeficiente intelectual medio muestral de 115 (barra x).
Por simplicidad, en esta pregunta, redondearemos z* = 1.96 a 2. Debe usar z* = 1.96 en todos los problemas a menos que se le indique específicamente que haga lo contrario.
Un intervalo de confianza del 95% para μ (mu) en este caso es:
\(\bar{x} \pm 2 \dfrac{\sigma}{\sqrt{n}}=115 \pm 2\left(\dfrac{15}{\sqrt{100}}\right)=115 \pm 3.0=(112,118)\)
Obsérvese que el margen de error es m = 3, y por lo tanto el ancho del intervalo de confianza es 6.
Ahora bien, ¿y si cambiamos ligeramente el problema aumentando el tamaño de la muestra, y suponemos que era 400 en lugar de 100?
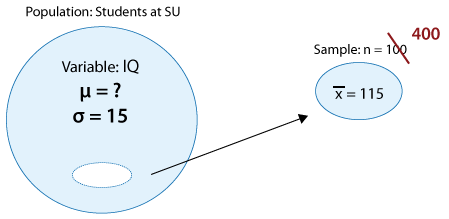
En este caso, un intervalo de confianza del 95% para μ (mu) es:
\(\bar{x} \pm 2 \dfrac{\sigma}{\sqrt{n}}=115 \pm 2\left(\dfrac{15}{\sqrt{400}}\right)=115 \pm 1.5=(113.5,116.5)\)
El margen de error aquí es solo m = 1.5, y así el ancho es de solo 3.
Tenga en cuenta que para el mismo nivel de confianza (95%) ahora tenemos un intervalo de confianza más estrecho y, por lo tanto, más preciso.
Tratemos de entender por qué es que un tamaño de muestra más grande reducirá el margen de error para un nivel fijo de confianza. Hay tres formas de explicar esto: matemáticamente, usando la teoría de la probabilidad, e intuitivamente.
Ya hemos aludido a la explicación matemática; el margen de error es
\(m = z* \dot \dfrac{\sigma}{\sqrt{n}}\)
y dado que n, el tamaño de la muestra, aparece en el denominador, aumentar n reducirá el margen de error.
Como vimos en nuestra discusión sobre estimaciones puntuales, la teoría de probabilidad nos dice que:
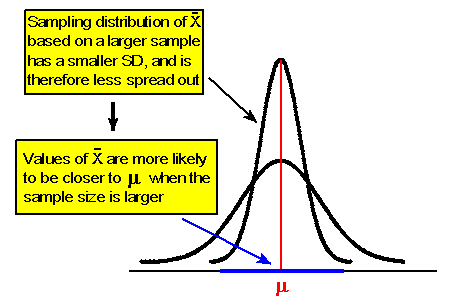
Esto explica por qué con un tamaño de muestra más grande el margen de error (que representa lo lejos que creemos que la barra x podría estar de μ (mu) para un nivel de confianza dado) es menor.
A nivel intuitivo, si nuestra estimación x-bar se basa en una muestra más grande (es decir, una fracción mayor de la población), tenemos más fe en ella, o es más confiable, y por lo tanto necesitamos dar cuenta de menos error a su alrededor.
Comentario:
- Si bien es cierto que para un determinado nivel de confianza, aumentar el tamaño de la muestra aumenta la precisión de nuestra estimación de intervalos, en la práctica, aumentar el tamaño de la muestra no siempre es posible.
- Considera un estudio en el que hay un costo no despreciable para recolectar datos de cada participante (un procedimiento médico costoso, por ejemplo). Si el estudio tiene algunas limitaciones presupuestales, como suele ser el caso, incrementar el tamaño de la muestra de 100 a 400 simplemente no es posible en términos de costo-efectividad.
- Otra instancia en la que es imposible aumentar el tamaño de la muestra es cuando una muestra más grande simplemente no está disponible, aunque tuviéramos el dinero para pagarla. Por ejemplo, considere un estudio sobre la efectividad de un medicamento en la curación de una enfermedad muy rara en niños. Dado que la enfermedad es rara, hay un número limitado de niños que podrían ser participantes.
- Esta es la realidad de las estadísticas. A veces la teoría choca con la realidad, y simplemente haces lo mejor que puedes.
¿Recibí esto? : Tamaño de la muestra y confianza
Medios de Población (Parte 3)
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.30: Interpretar intervalos de confianza para parámetros poblacionales en contexto.
Objetivos de aprendizaje
LO 4.31: Encuentre intervalos de confianza para la media poblacional usando la fórmula de intervalo de confianza basada en la distribución normal (Z) (cuando se cumplan las condiciones requeridas) y realice cálculos de tamaño de muestra.
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Objetivos de aprendizaje
LO 6.24: Explicar la conexión entre la distribución muestral de un estadístico, y sus propiedades como estimador puntual.
Objetivos de aprendizaje
LO 6.25: Explicar lo que representa un intervalo de confianza y determinar cómo los cambios en el tamaño de la muestra y el nivel de confianza afectan la precisión del intervalo de confianza.
Video
Video: Medios poblacionales — Parte 3 (6:02)
Cálculos de tamaño de muestra
Como acabamos de aprender, para un determinado nivel de confianza, el tamaño de la muestra determina el tamaño del margen de error y así el ancho, o precisión, de nuestra estimación del intervalo. Este proceso se puede revertir.
En situaciones donde un investigador tiene cierta flexibilidad en cuanto al tamaño de la muestra, el investigador puede calcular de antemano cuál es el tamaño de la muestra que necesita para poder reportar un intervalo de confianza con cierto nivel de confianza y cierto margen de error. Veamos un ejemplo.
EJEMPLO:
Recordemos el ejemplo sobre los puntajes SAT-M de estudiantes de colegios comunitarios.
Un investigador educativo está interesado en estimar μ (mu), la puntuación media en la parte de matemáticas del SAT (SAT-M) de todos los estudiantes de colegios comunitarios en su estado. Para ello, el investigador ha elegido una muestra aleatoria de 650 estudiantes de colegios comunitarios de su estado, y encontró que su puntaje promedio SAT-M es de 475. Con base en un gran cuerpo de investigación que se realizó en el SAT, se sabe que las puntuaciones siguen aproximadamente una distribución normal, con la desviación estándar σ (sigma) =100.
El intervalo de confianza del 95% para μ (mu) es
\ begin {aligned}
475\ pm 1.96 *\ frac {100} {\ sqrt {650}} &=\ left (475-1.96 *\ frac {100} {\ sqrt {650}}, 475+1.96 *\ frac {100} {\ sqrt {650}}\ derecha)\\ & =( 475-7.7.475+7.7)\\ & =( 467.7.475+7.7)\
& =( 467.7.475+7.7)\
& =( 467.7.475+7.7)\ 3,482.7)
\ final {alineado}
que es aproximadamente 475 ± 8, o (467, 483). Para un tamaño de muestra de n = 650, nuestro margen de error es 8.
Ahora, pensemos en este problema de una manera ligeramente diferente:
Un investigador educativo está interesado en estimar μ (mu), la puntuación media en la parte matemática del SAT (SAT-M) de todos los estudiantes de colegios comunitarios en su estado con un margen de error de (solo) 5, al nivel de confianza del 95%. ¿Cuál es el tamaño de muestra necesario para lograrlo? σ (sigma), por supuesto, todavía se supone que es 100.
Para resolver esto, establecemos:
\(m=2 \cdot \frac{100}{\sqrt{n}}=5 \quad \text { so } \quad \sqrt{n}=\frac{2(100)}{5} \quad \text { and } \quad n=\left(\frac{2(100)}{5}\right)^{2}=1600\)
Entonces, para un tamaño muestral de 1,600 estudiantes de colegios comunitarios, el investigador podrá estimar μ (mu) con un margen de error de 5, en el nivel 95%. En este ejemplo, también podemos imaginar que el investigador tiene cierta flexibilidad para elegir el tamaño de la muestra, ya que hay un costo mínimo (si lo hay) involucrado en registrar los puntajes SAT-M de los estudiantes, y hay muchos más de 1,600 estudiantes de colegios comunitarios en cada estado.
En lugar de tomar los mismos pasos para aislar n cada vez que resolvamos tal problema, podemos obtener una expresión general para el n requerido para un margen de error deseado m y un cierto nivel de confianza.
Desde
\(m = z* \dot \dfrac{\sigma}{\sqrt{n}}\)
es la fórmula para determinar m para un n dado, podemos usar álgebra simple para expresar n en términos de m (multiplicar ambos lados por la raíz cuadrada de n, dividir ambos lados por m, y cuadrar ambos lados) para obtener
\(n = (\dfrac{z* \sigma}{m})^2\)
Comentario:
- Claramente, el tamaño de muestra n debe ser un número entero.
- En el ejemplo anterior obtuvimos n = 1,600, pero en otras situaciones, el cálculo puede darnos un resultado no entero.
- En estos casos, siempre debemos redondear hasta el siguiente entero más alto.
- Usando este “enfoque conservador”, lograremos un intervalo al menos tan estrecho como el deseado.
EJEMPLO:
Se sabe que los puntajes de CI varían normalmente con una desviación estándar de 15. ¿Cuántos estudiantes deben ser muestreados si queremos estimar el coeficiente intelectual medio poblacional al 99% de confianza con un margen de error igual a 2?
\(n=\left(\dfrac{z^{*} \sigma}{m}\right)^{2}=\left(\dfrac{2.576(15)}{2}\right)^{2}=373.26\)
Redondear para estar seguros, y tomar una muestra de 374 alumnos.
El propósito de la siguiente actividad es darte práctica guiada en cálculos de tamaño de muestra para obtener intervalos de confianza con un margen de error deseado, a cierto nivel de confianza. Considera el ejemplo de la actividad anterior Aprender haciendo:
Aprender haciendo: Tamaño de la muestra
Comentario:
- En la actividad anterior, viste que para poder calcular el tamaño muestral al planear un estudio, necesitabas conocer la desviación estándar de la población, sigma (σ). En la práctica, normalmente no se conoce sigma, porque es un parámetro. (Las raras excepciones son ciertas variables como el puntaje de CI o pruebas estandarizadas que podrían construirse para tener una sigma conocida en particular).
Por lo tanto, cuando los investigadores desean calcular el tamaño de muestra requerido en preparación para un estudio, utilizan una estimación de sigma. Por lo general, la sigma se estima con base en la desviación estándar obtenida en estudios previos.
Sin embargo, en algunos casos, puede que no haya estudios previos sobre el tema. En tales casos, un investigador aún necesita obtener una estimación aproximada de la desviación estándar de la variable (aún por medir), para determinar el tamaño de muestra requerido para el estudio. Una forma de obtener una estimación tan aproximada es con la “regla general de rango”. No cubriremos este tema en profundidad pero mencionaremos aquí que una estimación muy aproximada de la desviación estándar de una población es el rango/4.
Hay algunas cosas más que debemos discutir:
- ¿Siempre está bien usar el intervalo de confianza que desarrollamos para μ (mu) cuando se conoce σ (sigma)?
- ¿Qué pasa si σ (sigma) es desconocida?
- ¿Cómo podemos usar el software estadístico para calcular los intervalos de confianza para nosotros?
¿Cuándo es seguro usar el intervalo de confianza que desarrollamos?
Una de las cosas más importantes para aprender con cualquier método de inferencia son las condiciones bajo las cuales es seguro usarlo. Es muy tentador aplicar cierto método, pero si no se cumplen las condiciones bajo las cuales se desarrolló este método, entonces el uso de este método conducirá a resultados poco confiables, que luego pueden llevar a conclusiones equivocadas y/o engañosas. Como verás a lo largo de esta sección, siempre discutiremos las condiciones bajo las cuales cada método puede ser utilizado de manera segura.
En particular, el intervalo de confianza para μ (mu), cuando se conoce σ (sigma):
\(\bar{x} \pm z* \dot \dfrac{\sigma}{\sqrt{n}}\)
se desarrolló asumiendo que la distribución muestral de la barra x es normal; es decir, que se aplica el Teorema del Límite Central. En particular, esto nos permitió determinar los valores de z*, el multiplicador de confianza, para diferentes niveles de confianza.
Primero, la muestra debe ser aleatoria. Suponiendo que la muestra es aleatoria, recuerde de la unidad Probabilidad que el Teorema del Límite Central funciona cuando el tamaño de la muestra es grande (una regla general común para “grande” es n > 30), o, para tamaños de muestra más pequeños, si se sabe que la variable cuantitativa de el interés se distribuye normalmente en la población. La única situación en la que no podemos usar el intervalo de confianza, entonces, es cuando el tamaño de la muestra es pequeño y no se sabe que la variable de interés tenga una distribución normal. En ese caso, es necesario utilizar otros métodos, llamados métodos no paramétricos, que están más allá del alcance de este curso. Esto se puede resumir en la siguiente tabla:
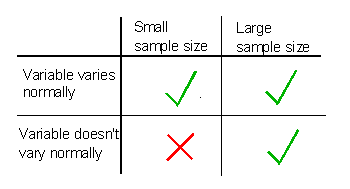
¿Recibí esto? : Cuándo usar el intervalo Z (medias)
En la siguiente actividad, se tiene la oportunidad de utilizar software para resumir los datos brutos proporcionados.
¿Recibí esto? : Intervalos de confianza: Media #3
¿Qué pasa si σ (sigma) es desconocida?
Como comentamos anteriormente, cuando las variables han sido bien investigadas en diferentes poblaciones es razonable suponer que se conoce la desviación estándar poblacional (σ, sigma). Sin embargo, este rara vez es el caso. ¿Qué pasa si σ (sigma) es desconocida?
Bueno, hay algunas buenas noticias y algunas malas noticias.
La buena noticia es que podemos sustituir fácilmente la desviación estándar poblacional, σ (sigma), con la desviación estándar muestral, s.
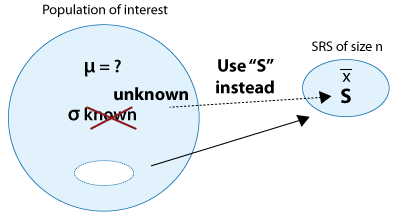
La mala noticia es que una vez que σ (sigma) ha sido sustituido por s, perdemos el Teorema del Límite Central, junto con la normalidad de la barra x, y por lo tanto los multiplicadores de confianza z* para los diferentes niveles de confianza (1.645, 1.96, 2.576) ya no son (generalmente) correctos. Los nuevos multiplicadores provienen de una distribución diferente llamada “distribución t” y por lo tanto se denotan con t* (en lugar de z*). Discutiremos la distribución t con más detalle cuando se hable de pruebas de hipótesis.
El intervalo de confianza para la media poblacional (μ, mu) cuando se desconoce (σ, sigma) es por lo tanto:
\(\bar{x} \pm t^{*} * \dfrac{s}{\sqrt{n}}\)
(Obsérvese que este intervalo es muy similar al que se conoce σ (sigma), con los cambios obvios: s reemplaza σ (sigma), y t* reemplaza a z* como se discutió anteriormente.)
Existe una diferencia importante entre los multiplicadores de confianza que hemos utilizado hasta ahora (z*) y los necesarios para el caso cuando σ (sigma) es desconocido (t*). A diferencia de los multiplicadores de confianza que hemos utilizado hasta ahora (z*), que dependen únicamente del nivel de confianza, los nuevos multiplicadores (t*) tienen la complejidad añadida que dependen tanto del nivel de confianza como del tamaño de la muestra (por ejemplo: el t* utilizado en una confianza del 95% cuando n = 10 es diferente del t* utilizado cuando n = 40). Debido a esta complejidad añadida para determinar el t* apropiado, confiaremos en gran medida en el software en este caso.
Comentarios:
- Como es bastante raro que se conozca σ (sigma), este intervalo (a veces llamado “intervalo de confianza t de una muestra”) se usa más comúnmente como el intervalo de confianza para estimar μ (mu). (Sin embargo, no podríamos haberlo presentado sin nuestra discusión extendida hasta este punto, que también le proporcionó una sólida comprensión de los intervalos de confianza.)
- La cantidad s/sqrt (n) se llama el error estándar estimado de x-bar. El Teorema del Límite Central nos dice que σ/sqrt (n) = sigma/sqrt (n) es la desviación estándar de x-bar (y esta es la cantidad utilizada en el intervalo de confianza cuando se conoce σ (sigma)). En general, el error estándar es la desviación estándar de la distribución muestral de un estadístico. Cuando sustituimos s por σ (sigma) estamos estimando el verdadero error estándar. Es posible que vea el término “error estándar” utilizado tanto para el error estándar verdadero como para el error estándar estimado dependiendo del autor y la audiencia. Lo importante de entender sobre el error estándar es que mide la variación de una estadística calculada a partir de una muestra de un tamaño de muestra especificado (no la variación de la población original).
- Como antes, para utilizar de manera segura este intervalo de confianza (intervalo de confianza t de una muestra), la muestra debe ser aleatoria, y el único caso en el que este intervalo no se puede usar es cuando el tamaño de la muestra es pequeño y no se sabe que la variable varíe normalmente.
Comentario Final:
- Resulta que para valores grandes de n, los multiplicadores t* no son tan diferentes de los multiplicadores z*, y por lo tanto usando la fórmula de intervalo:
\(\bar{x} \pm z* \ast \dfrac{s}{\sqrt{n}}\)
para μ (mu) cuando σ (sigma) es desconocido proporciona una aproximación bastante buena.
Medios de Población (Resumen)
Vamos a resumir
- Cuando la población es normal y/o la muestra es grande, un intervalo de confianza para la población desconocida media μ (mu) cuando se conoce σ (sigma) es:
\(\bar{x} \pm z* \dot \dfrac{\sigma}{\sqrt{n}}\)
donde z* es 1.645 para 90% de confianza, 1.96 para 95% de confianza y 2.576 para 99% de confianza.
- Existe un compromiso entre el nivel de confianza y la precisión de la estimación del intervalo. Para un tamaño de muestra dado, el precio que tenemos que pagar por más precisión es sacrificar el nivel de confianza.
- La forma general de intervalos de confianza es una estimación +/- el margen de error (m). En este caso, la estimación = x-bar y
\(m = z* \dot \dfrac{\sigma}{\sqrt{n}}\)
Por lo tanto, el intervalo de confianza se centra en la estimación y su ancho es exactamente de 2m.
- Para un determinado nivel de confianza, el ancho del intervalo depende del tamaño de la muestra. Por lo tanto, podemos hacer un cálculo del tamaño de la muestra para determinar qué tamaño de muestra se necesita para obtener un intervalo de confianza con un margen de error deseado m, y un cierto nivel de confianza (asumiendo que tenemos cierta flexibilidad con el tamaño de la muestra). Para hacer el cálculo del tamaño de la muestra utilizamos:
\(n =( \dfrac{z* \sigma}{m})^2\)
(y redondear hasta el siguiente entero). Estimamos σ (sigma) cuando sea necesario.
- Cuando σ (sigma) es desconocida, usamos la desviación estándar de la muestra, s, en su lugar, pero como resultado también necesitamos usar un conjunto diferente de multiplicadores de confianza (t*) asociados a la distribución t. Utilizaremos software para calcular intervalos en este caso, sin embargo, la fórmula para el intervalo de confianza en este caso es
\(\bar{x} \pm t* \ast \dfrac{s}{\sqrt{n}}\)
- Estos nuevos multiplicadores tienen la complejidad añadida de que dependen no sólo del nivel de confianza, sino también del tamaño de la muestra. Por lo tanto, el software es muy útil para calcular intervalos de confianza en este caso.
- Para valores grandes de n, los multiplicadores t* no son tan diferentes de los multiplicadores z*, y por lo tanto usan la fórmula de intervalo:
\(\bar{x} \pm z* \ast \dfrac{s}{\sqrt{n}}\)
para μ (mu) cuando σ (sigma) es desconocido proporciona una aproximación bastante buena.
Proporciones de Población
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.30: Interpretar intervalos de confianza para parámetros poblacionales en contexto.
Objetivos de aprendizaje
LO 4.32: Encuentre intervalos de confianza para la proporción poblacional usando la fórmula (cuando se cumplan las condiciones requeridas) y realice cálculos de tamaño de muestra.
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Objetivos de aprendizaje
LO 6.24: Explicar la conexión entre la distribución muestral de un estadístico, y sus propiedades como estimador puntual.
Objetivos de aprendizaje
LO 6.25: Explicar lo que representa un intervalo de confianza y determinar cómo los cambios en el tamaño de la muestra y el nivel de confianza afectan la precisión del intervalo de confianza.
Video
Video: Proporciones poblacionales (4:13)
Intervalos de confianza
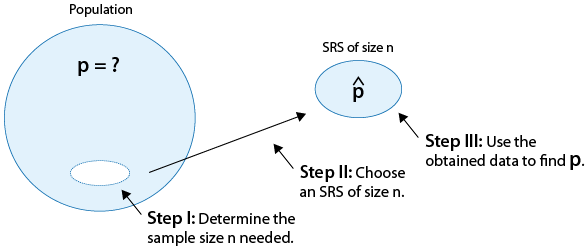
Como mencionamos en la introducción a la Unidad 4A, cuando la variable que nos interesa estudiar en la población es categórica, el parámetro que estamos tratando de inferir es la proporción poblacional (p) asociada a esa variable. También aprendimos que el estimador puntual para la proporción poblacional p es la proporción muestral p-hat.
Para refrescar tu memoria, aquí tienes una imagen que resume un ejemplo que miramos.
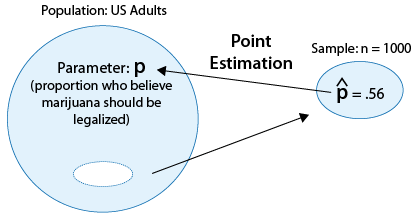
Ahora estamos pasando a la estimación de intervalos de p. En otras palabras, nos gustaría desarrollar un conjunto de intervalos que, con diferentes niveles de confianza, capturen el valor de p. De hecho, hemos hecho todo el trabajo preliminar y discutido todas las grandes ideas de estimación de intervalos cuando hablamos de intervalo estimación para μ (mu), así podremos atravesarlo mucho más rápido. Empecemos.
Recordemos que la forma general de cualquier intervalo de confianza para un parámetro desconocido es:
estimación ± margen de error
Dado que el parámetro desconocido aquí es la proporción poblacional p, el estimador de puntos (como te recordé anteriormente) es la proporción muestral p-hat. El intervalo de confianza para p, por lo tanto, tiene la forma:
![]()
(Recordemos que m es la notación para el margen de error.) El margen de error (m) nos da el error máximo de estimación con cierta confianza. En este caso nos dice que p-hat es diferente de p (el parámetro que estima) en no más de m unidades.
De nuestra anterior discusión sobre los intervalos de confianza, también sabemos que el margen de error es producto de dos componentes:
![]()
Para averiguar cuáles son estos dos componentes, necesitamos volver a un resultado que obtuvimos en la sección Distribuciones de Muestreo de la unidad Probabilidad sobre la distribución muestral de p-hat. Encontramos que bajo ciertas condiciones (a las que volveremos más adelante), p-hat tiene una distribución normal con p media, y a
![]()
Este resultado nos hace las cosas muy simples, porque revela cuáles son los dos componentes de los que está hecho el margen de error:
- Dado que, al igual que la distribución de muestreo de x-bar, la distribución de muestreo de p-hat es normal, los multiplicadores de confianza que usaremos en el intervalo de confianza para p serán los mismos multiplicadores z* que usamos para el intervalo de confianza para μ (mu) cuando se conoce σ (sigma) (usando exactamente lo mismo razonamiento y los mismos resultados probabilísticos). Los multiplicadores que usaremos, entonces, son: 1.645, 1.96 y 2.576 a los niveles de confianza del 90%, 95% y 99%, respectivamente.
- La desviación estándar de nuestro estimador p-hat es
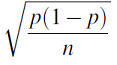
Poniéndolo todo junto, encontramos que el intervalo de confianza para p debería ser:
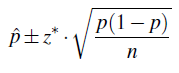
Sólo tenemos que resolver un problema práctico y ya terminamos. Estamos tratando de estimar la proporción de población desconocida p, por lo que no tiene sentido que aparezca en el intervalo de confianza. Para superar este problema, haremos lo obvio...
Reemplazaremos p con su contraparte de muestra, p-hat, y trabajaremos con el error estándar estimado de p-hat
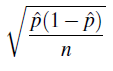
Ahora ya terminamos. El intervalo de confianza para la proporción poblacional p es:
\(\hat{p} \pm z^{*} \cdot \sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)
EJEMPLO:
El medicamento Viagra estuvo disponible en Estados Unidos en mayo de 1998, a raíz de una campaña publicitaria que no tuvo precedentes en alcance e intensidad. Una encuesta de Gallup encontró que al final de la primera semana de mayo, 643 de una muestra aleatoria de 1,005 adultos estaban al tanto de que Viagra era un medicamento para la impotencia (basado en “Viagra A Popular Hit”, un análisis de encuesta de Gallup de Lydia Saad, mayo de 1998).
Estimemos la proporción p de todos los adultos en Estados Unidos que a finales de la primera semana de mayo de 1998 ya estaban al tanto del Viagra y su propósito estableciendo un intervalo de confianza del 95% para la p.
Primero necesitamos calcular la proporción muestral p-hat. De 1,005 adultos muestreados, 643 sabían para qué se utiliza Viagra, así que p-hat = 643/1005 = 0.64
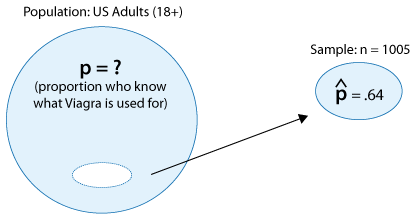
Por lo tanto, un intervalo de confianza del 95% para p es
\ begin {alineado}
\ hat {p}\ pm 1.96\ cdot\ sqrt {\ frac {\ hat {p} (1-\ hat {p})} {n}} &=0.64\ pm 1.96\ cdot\ sqrt {\ frac {0.64 (1-0.64)} {1005}}\\
&=0.64\ pm 0.03\\
& =( 0.61,0.0 67)
\ end {alineado}
Podemos estar 95% seguros de que la proporción de todos los adultos estadounidenses que ya estaban familiarizados con Viagra en ese momento estaba entre 0.61 y 0.67 (o 61% y 67%).
El hecho de que el margen de error sea igual a 0.03 dice que podemos estar 95% seguros de que la proporción de población desconocida p está dentro de 0.03 (3%) de la proporción de muestra observada 0.64 (64%). En otras palabras, estamos 95% seguros de que el 64% está “apagado” en no más del 3%.
¿Conseguí esto? : Intervalos de confianza — Proporciones #1
Comentario:
- Nos gustaría compartir con ustedes la parte de metodología del lanzamiento oficial de la encuesta para el ejemplo de Viagra. Esperamos que veas que ahora tienes las herramientas para entender cómo se analizan los resultados de las encuestas:
“Los resultados se basan en entrevistas telefónicas a una muestra nacional seleccionada al azar de 1,005 adultos, de 18 años en adelante, realizadas del 8 al 10 de mayo de 1998. Para resultados basados en muestras de este tamaño, se puede decir con 95 por ciento de confianza que el error atribuible al muestreo y otros efectos aleatorios podría ser más o menos 3 puntos porcentuales. Además del error de muestreo, la redacción de las preguntas y las dificultades prácticas en la realización de encuestas pueden introducir error o sesgo en los hallazgos de las encuestas de opinión pública”.
El propósito de la siguiente actividad es proporcionar una práctica guiada en el cálculo e interpretación del intervalo de confianza para la proporción poblacional p, y sacar conclusiones a partir de ella.
Aprende haciendo: Intervalos de confianza — Proporciones #1
Dos resultados importantes que discutimos extensamente cuando hablamos del intervalo de confianza para μ (mu) también se aplican aquí:
1. Existe una compensación entre el nivel de confianza y el ancho (o precisión) del intervalo de confianza. Cuanta más precisión le gustaría que tuviera el intervalo de confianza para p, más tendrá que pagar al tener un menor nivel de confianza.
2. Dado que n aparece en el denominador del margen de error del intervalo de confianza para p, para un nivel fijo de confianza, cuanto mayor sea la muestra, más estrecha o más precisa es. Esto nos lleva naturalmente a nuestro siguiente punto.
Cálculos de tamaño de muestra
Así como lo hicimos para las medias, cuando tenemos cierto nivel de flexibilidad en la determinación del tamaño de la muestra, podemos establecer un margen de error deseado para estimar la proporción poblacional y encontrar el tamaño de la muestra que lo logrará.
Por ejemplo, una encuesta final el día anterior a una elección querría que el margen de error fuera bastante pequeño (con un alto nivel de confianza) para poder predecir los resultados electorales con la mayor precisión. Esto es particularmente relevante cuando se trata de una carrera cercana entre los candidatos. La empresa de encuestas necesita averiguar cuántos votantes elegibles necesita incluir en su muestra para lograrlo.
Veamos cómo lo hacemos.
(Comentario: Para nuestra discusión aquí nos centraremos en un nivel de confianza del 95% (z* = 1.96), ya que este es el nivel de confianza más utilizado.)
El intervalo de confianza para p es
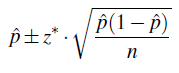
El margen de error, entonces, es
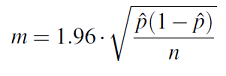
Ahora aislamos n (es decir, expresarlo en función de m).
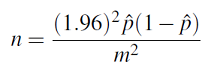
Hay un problema práctico con esta expresión que debemos superar.
Prácticamente, primero determinas el tamaño de la muestra, luego eliges una muestra aleatoria de ese tamaño y luego usas los datos recopilados para encontrar p-hat.
Entonces, el hecho de que la expresión anterior para determinar el tamaño de la muestra dependa de p-hat es problemático.
La manera de superar este problema es tomar el enfoque conservador estableciendo p-hat = 1/2 = 0.5.
¿Por qué llamamos conservador a este enfoque?
Es conservadora porque la expresión que aparece en el numerador,
![]()
se maximiza cuando p-hat = 1/2 = 0.5.
De esa manera, la n que obtengamos trabajará en darnos el margen de error deseado independientemente de cuál sea el valor de p-hat. Este es un enfoque de “peor de los casos”. Entonces cuando hacemos eso obtenemos:
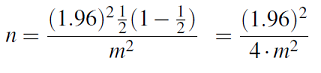
En general, para cualquier nivel de confianza tenemos
- Si conocemos una estimación razonable de la proporción podemos utilizar:
\(n=\dfrac{\left(z^{*}\right)^{2} \hat{p}(1-\hat{p})}{m^{2}}\)
- Si elegimos la estimación conservadora asumiendo que no sabemos nada sobre la verdadera proporción que usamos:
\(n=\dfrac{\left(z^{*}\right)^{2}}{4 \cdot m^{2}}\)
EJEMPLO:
Parece que las encuestas mediáticas suelen utilizar un tamaño de muestra de 1,000 a 1,200. Esto podría ser desconcertante.
¿Cómo podrían los resultados obtenidos de, digamos, 1,100 adultos estadounidenses darnos información sobre toda la población de adultos estadounidenses? 1,100 es una fracción tan diminuta de la población real. Aquí está la respuesta:
¿Qué tamaño de muestra n se necesita si se desea un margen de error m = 0.03?
\(n=\dfrac{(1.96)^{2}}{4 \cdot(0.03)^{2}}=1067.1 \rightarrow 1068\)
(recuerda, siempre redondear). De hecho, el 0.03 es un margen de error muy utilizado, especialmente para las encuestas mediáticas. Por ello, la mayoría de las encuestas mediáticas trabajan con una muestra de alrededor de 1,100 personas.
¿Recibí esto? : Intervalos de confianza — Proporciones #2
¿Cuándo es seguro usar estos métodos?
Como mencionamos anteriormente, una de las cosas más importantes para aprender con cualquier método de inferencia son las condiciones bajo las cuales es seguro usarlo.
Como hicimos para la media, la suposición que hicimos para desarrollar los métodos en esta unidad fue que la distribución muestral de la proporción muestral, p-hat es aproximadamente normal. Recordemos de la unidad de Probabilidad que las condiciones bajo las cuales esto sucede son que
\(n p \geq 10 \text { and } n(1-p) \geq 10\)
Dado que p es desconocida, la reemplazaremos con su estimación, la proporción muestral y estableceremos
\(n \hat{p} \geq 10 \text { and } n(1-\hat{p}) \geq 10\)
ser las condiciones bajo las cuales es seguro utilizar los métodos que desarrollamos en esta sección.
Aquí hay una práctica final para estos intervalos de confianza!!
¿Recibí esto? : Intervalos de confianza — Proporciones #3
Vamos a resumir
En general, un intervalo de confianza para la proporción de población desconocida (p) es
\(\hat{p} \pm z^{*} \cdot \sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)
donde z* es 1.645 para 90% de confianza, 1.96 para 95% de confianza y 2.576 para 99% de confianza.
Para obtener un margen de error deseado (m) en un intervalo de confianza para una proporción de población desconocida, un tamaño de muestra conservador es
\(n=\dfrac{\left(z^{*}\right)^{2}}{4 \cdot m^{2}}\)
Si se conoce una estimación razonable de la proporción verdadera, el tamaño de la muestra se puede calcular usando
\(n = \dfrac{(1.96)^2 \hat{p} (1-\hat{p})}{m^2}\)
Los métodos desarrollados en esta unidad son seguros de usar siempre y cuando
\(n \hat{p} \geq 10 \text{ and } n(1-\hat{p}) \geq 10\)
Resumen (estimación)
En esta sección de estimación, hemos discutido el proceso básico para construir intervalos de confianza a partir de estimaciones puntuales. Al hacerlo debemos calcular el margen de error utilizando el error estándar (o error estándar estimado) y un valor z* o t*.
Al concluir este tema, quisimos volver a discutir la interpretación de un intervalo de confianza.
¿Qué queremos decir con “confianza”?
Supongamos que encontramos un intervalo de confianza del 95% para un parámetro desconocido, ¿qué significa exactamente el 95%?
- Si repetimos el proceso para todas las muestras posibles de este tamaño para la población, el 95% de los intervalos que construimos contendrá el parámetro
Esto NO es lo mismo que decir “la probabilidad de que μ (mu) esté contenido en (el intervalo construido a partir de mi muestra) es del 95%. ” ¿Por qué?
Contestar
- Una vez que tenemos un intervalo de confianza particular, el valor verdadero está o bien en el intervalo construido a partir de nuestra muestra (probabilidad = 1) o no lo está (probabilidad = 0). Simplemente no sabemos cuál es. Si dijéramos “la probabilidad de que μ (mu) esté contenido en (el intervalo construido a partir de mi muestra) es del 95%”, sabemos que seríamos incorrectos ya que es 0 (No) o 1 (Sí) para cualquier muestra dada. La probabilidad proviene de la visión “a largo plazo” del proceso.
- La probabilidad que utilizamos para construir el intervalo de confianza se basó en el hecho de que el estadístico muestral (x-bar, p-hat) variará de una manera que entendemos (porque conocemos la distribución muestral).
- La probabilidad se asocia con la aleatoriedad de nuestra estadística de manera que para un intervalo determinado solo hablamos de tener “95% de confianza” lo que se traduce en una comprensión sobre el proceso.
- Es decir, en estadística, “95% confiado” significa nuestra confianza en el proceso e implica que a la larga, estaremos en lo correcto al usar este proceso el 95% del tiempo pero ese 5% del tiempo seremos incorrectos. Para un uso particular de este proceso no podemos saber si somos uno de los 95% que son correctos o uno de los 5% que son incorrectos. Esa es la definición estadística de confianza.
- Podemos decir que a la larga, 95% de estos intervalos contendrán el parámetro verdadero y 5% no lo hará.
Interpretaciones correctas:
Ejemplo: Supongamos que un intervalo de confianza del 95% para la proporción de adultos estadounidenses que no están activos en absoluto es (0.23, 0.27).
- Interpretación correcta #1: Estamos 95% seguros de que la verdadera proporción de adultos estadounidenses que no son activos en absoluto está entre 23% y 27%
- Interpretación Correcta #2: Estamos 95% seguros de que la verdadera proporción de adultos estadounidenses que no están activos en absoluto está cubierta por el intervalo (23%, 27%)
- Una interpretación más exhaustiva: Con base en nuestra muestra, se estima que la verdadera proporción de adultos estadounidenses que no están activos en absoluto es del 25%. Con 95% de confianza, este valor podría ser tan pequeño como 23% a tan grande como 27%.
- Una interpretación común en artículos de revistas: Con base en nuestra muestra, la verdadera proporción de adultos estadounidenses que no están activos en absoluto se estima en 25% (IC 95% 23%-27%).
Ahora veamos una interpretación INCORRECTA que hemos visto antes
- Interpretación INCORRECTA: Existe un 95% de probabilidad de que la verdadera proporción de adultos estadounidenses que no están activos en absoluto esté entre 23% y 27%. Sabemos que esto es incorrecto porque en este punto, la verdadera proporción y los números en nuestro intervalo son fijos. La probabilidad es de 1 o 0 dependiendo de si el intervalo es uno de los 95% que cubren la verdadera proporción, o uno de los 5% que no.
Para los intervalos de confianza respecto a una media poblacional, tenemos una precaución adicional para discutir sobre las interpretaciones.
Ejemplo: Supongamos que un intervalo de confianza del 95% para el promedio de minutos diarios de ejercicio para adultos estadounidenses es (12, 18).
- Interpretación correcta: Estamos 95% seguros de que la verdadera media de minutos diarios de ejercicio para adultos estadounidenses es de entre 12 y 18 minutos.
- Interpretación INCORRECTA: Estamos 95% seguros de que un adulto individual de Estados Unidos ejerce entre 12 y 18 minutos diarios. Debemos recordar que nuestros intervalos son sobre el parámetro, en este caso la media poblacional. No se aplican a un individuo ya que esperamos que los individuos tengan mucha más variación.
- Interpretación INCORRECTA: Estamos 95% seguros de que los adultos estadounidenses hacen ejercicio entre 12 y 18 minutos al día.Esta interpretación implica que esto es cierto para todos los adultos estadounidenses. ¡Esta es una interpretación incorrecta por la misma razón que la interpretación incorrecta anterior!
A medida que continuemos estudiando estadísticas inferenciales, veremos que los intervalos de confianza se utilizan en muchas situaciones. El objetivo es siempre brindar confianza en nuestra estimación de intervalo de una cantidad de interés. Las medias y proporciones poblacionales son parámetros comunes, sin embargo, cualquier cantidad que pueda estimarse a partir de los datos tiene una contraparte poblacional que tal vez deseemos estimar.
(Opcional) Lectura Exterior: Pequeño Manual — Intervalos de Confianza (y Más) (4 Lecturas, ≈ 5500 palabras)

