13.6: Análisis Post-hoc — Prueba de Diferencia Honestamente Significativa (HSD) de Tukey85
- Page ID
- 151415
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cuando se rechaza la Hipótesis Null en un factor ANOVA, la conclusión es que no todas las medias son iguales. Esto, sin embargo, lleva a una pregunta obvia: ¿qué medios particulares son diferentes? La búsqueda de más información después de los resultados de una prueba se denomina análisis post hoc.
El problema de las pruebas múltiples
Un intento de responder a esta pregunta es realizar múltiples pruebas t‐independientes por pares y determinar cuáles son significativas. Nos compararíamos\(\mu_{1}\) con\(\mu_{2}\),\(\mu_{1}\) a\(\mu_{3}\),\(\mu_{2}\) a\(\mu_{3}\),\(\mu_{1}\) a\(\mu_{4}\), etc. Existe una falla importante en esta metodología en el sentido de que cada prueba tendría un nivel de significancia de\(\alpha\), por lo que hacer el error Tipo I sería significativamente más que el deseado \(\alpha\). Además, estas pruebas por pares NO serían mutuamente independientes. Hubo varios estadísticos que diseñaron pruebas que abordaron efectivamente este problema de determinar un nivel de significancia “honesto” de un conjunto de pruebas; cubriremos la desarrollada por John Tukey, la prueba Honestamente Significante Diferencia (HSD). 86 Para utilizar esta prueba, necesitamos el valor crítico de la Distribución de Rango Studentized (\(q\)), que se utiliza para encontrar cuando la diferencia de pares de medias de muestra es significativa.
La prueba Tukey HSD
Pruebas:\(H_{o}: \mu_{i}=\mu_{j} \quad H_{a}: \mu_{i} \neq \mu_{j}\) donde los subíndices\(i\) y\(j\) representan dos poblaciones diferentes
Nivel de significancia general de\(\alpha\): Esto significa que todas las pruebas por pares se pueden ejecutar al mismo tiempo con un nivel de significancia general de\(\alpha\)
Estadística de prueba:\(\mathrm{HSD}=q \sqrt{\dfrac{\mathrm{MSE}{n_{c}}}\)
\(q\)= valor crítico de la tabla Rango Studentized
\(\mathrm{MSE}\)= Error cuadrático medio de la tabla ANOVA
\(n_c\)= número de repeticiones por tratamiento. Se realiza un ajuste para diseños desequilibrados.
Decisión: Rechazar\(H_o\) si\(\left|\overline{X}_{i}-\overline{X}_{j}\right|>\mathrm{HSD}_\text{critical value}\)
Los programas informáticos, como Minitab, calcularán los valores críticos y probarán las estadísticas para estas series de pruebas. No realizaremos los cálculos manuales en este texto.
Volvamos al ejemplo de la pizza Tofu donde rechazamos la Hipótesis Null y apoyamos la afirmación de que había una diferencia de medias entre los tres restaurantes.
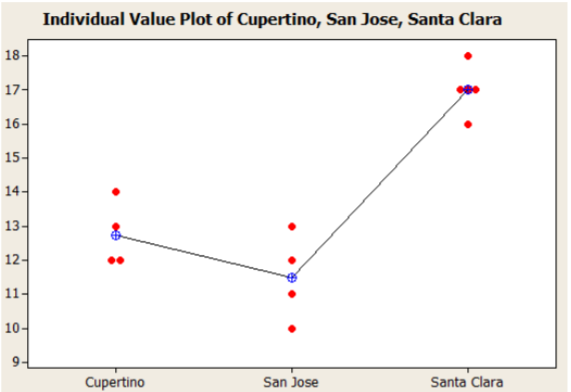
Al revisar la gráfica de las medias muestrales, parece que Santa Clara tiene un número de ventas mucho mayor que Cupertino y San José. Habrá tres pruebas pos‐hoc por pares para ejecutar.
Solución
Diseño
\(H_{o}: \mu_{1}=\mu_{2} \qquad H_{a}: \mu_{1} \neq \mu_{2} \qquad H_{o}: \mu_{1}=\mu_{3} \qquad H_{a}: \mu_{1} \neq \mu_{3} \qquad H_{o}: \mu_{2}=\mu_{3} \qquad H_{a}: \mu_{2} \neq \mu_{3}\)
Estas tres pruebas se realizarán con un nivel de significancia general de\(\alpha\) = 5%.
El modelo será la\(\mathrm{HSD}\) prueba de Tukey.
Aquí están las diferencias de las medias muestrales para cada par clasificado de menor a mayor:
Prueba 1: Cupertino a San José:\(\left|\overline{X}_{1}-\overline{X}_{2}\right|=|12.75-11.50|=1.25\)
Prueba 2: Cupertino a Santa Clara:\(\left|\overline{X}_{1}-\overline{X}_{3}\right|=|12.75-17.00|=4.25\)
Prueba 3: San José a Santa Clara:\(\left|\overline{X}_{2}-\overline{X}_{3}\right|=|11.50-17.00|=5.50\)
Los valores\(\mathrm{HSD}\) críticos (usando software estadístico) para esta prueba en particular:
\(\mathrm{HSD}_\text{crit}\)al nivel de significancia del 5% = 1.85\(\mathrm{HSD}_\text{crit}\) al nivel de significancia del 1% = 2.51
Para cada prueba, rechazar\(H_o\) si la diferencia de medias es mayor que\(\mathrm{HSD}_\text{crit}\)
La prueba 2 y la prueba 3 muestran medias significativamente diferentes tanto a nivel de 1% como de 5%.
El enfoque del Minitab para la regla de decisión será rechazar\(H_o\) por cada par que no comparta un grupo común. Estos son los resultados de la prueba realizada en el nivel de significancia del 5%:
Datos/Resultados
Consulte la salida de Minitab. Santa Clara está en el grupo A mientras que Cupertino y San José están en el Grupo B.

Conclusión
Santa Clara tiene una media significativamente mayor de pizzas de tofu vendidas en comparación con San José y Cupertino. No hay diferencia significativa en las ventas medias entre San José y Cupertino.


